基于改进PCA法在水资源承载力中的应用

望开发

（宜昌市夷陵区三斗坪水利管理站，湖北宜昌443100）

水资源承载力是一个与社会经济、生态环境相关联，衡量水资源可持续利用的重要指标，对于实行最严格水资源管理制度的“三条红线”控制具有重要意义。国内外学者在这领域已有很多研究成果，主要涉及的研究成果在概念、模型探讨、方法理论研究等方面，比如，T.Nakayama，Y.Sun，Y.Geng［1］基于流域生态水文（NICE）模型应用于华北的碧流河流域，估计水资源的承载能力；Harris等［2］从供水的角度对城市水资源承载力进行了相关研究，并考虑纳入城市发展规划当中的经济手段与政策措施研究； 熊黑钢等［3］针对新疆奇台绿洲水资源现实情况为例，构建水资源水资源承载力指标体系，应用主成分分析法计算，分析得到5大影响因素，为绿洲可持续发展提供依据；陈凯等［4］分别建立RBF神经网络模型、BP神经网络模型、模糊层次综合评价模型，对汕头市水资源承载力状况进行研究，比较出适用性更强的数学模型。水资源承载力评价采用的数学方法主要有层次分析法［5］、系统动力学法［6］、投影寻踪法［7］、多目标决策法［8］、数据包络分析［9］等，每种方法都有各自特点和使用范围。总体上，水资源承载力研究正从概念、计算方法的初级阶段逐步向系统复杂、理论科学统一的体系转变。

1 研究方法

1.1 传统主成分分析法

1.1.1 基本原理［10］

假设m个观测样本，有n个相互间有相互关联指标，可得到原始数据样本矩阵X=（X1，X2，X3，…，Xn）

根据样本矩阵X中的n个指标向量X1，X2，X3，…，Xn进行线性组合：

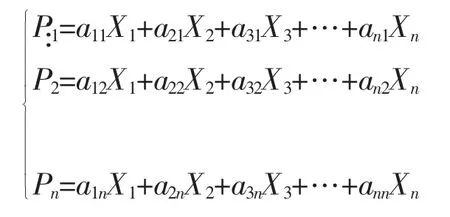
可简化为：

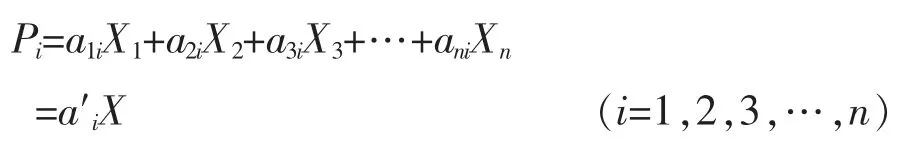
此方程组的解是求解系数矩阵ai的解，根据ai的解可对每个样品求出Pi值，由求出来的n个Pi值就能得到一个方差，记为Var（Pi），满足Var（P1）>>Var（P2）>…>Var（Pn）关系，确定P1，P2，P3，…，Pn成为主成分。

1.1.2 主要步骤

原始数据标准化如式（1）：

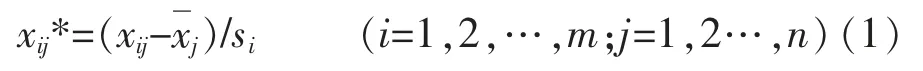
式中 xij为原始数据值；xij*标准化处理值；和sj为第j个指标样本均值和标准差。

通过相关系数矩阵S*=（Sij）*，计算特征值与对应特征向量。

由特征值从大到小进行排列，记为γ1>γ2>…>γn，相应的特征值对应的特征向量为βi=（β1i，β2i，β3i，…，βni）′。根据特征向量主成分如式（2）：

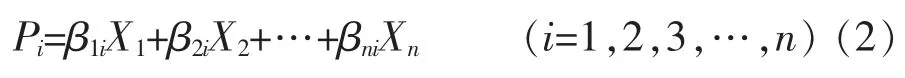
方差贡献率计算如式（3）：

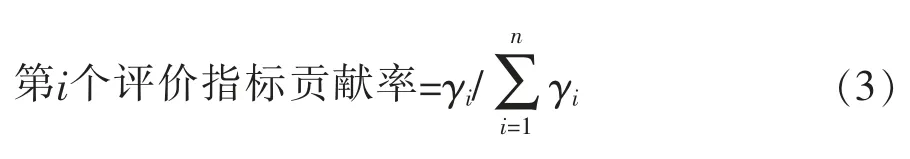
分析中，一般情况下不考虑n个主成分，其累计频率达85%以上主成分即可。

以确定各主成分的特征值与所提取主成分特征值之和的比值作为权重，即各主成分的方差贡献率，如式（4）。

主成分综合评价指数P如式（5）。

式中 ki为主成分权重；Pi为主成分（i=1，2，…，k）。

1.2 改进主成分分析法［11］

传统主成分分析法要求降维后信息量必须保持在一个较高水平上，并对这些信息量给予实际背景和意义的解释，主成分是一个综合指标，具有一定模糊性，在进行数据标准化处理后，可避免评价指标量纲值或数量级对组成相关系数矩阵的影响，同时也消除了原始评价指标之间的差异性，原始评价指标包含两层含义，①各个指标之间的相互联系程度，由相关系数矩阵得到；②各个指标之间的差异信息，由数据方差体现。传统意义上的主成分分析，在数据标准化处理后，评价指标均值0，方差1，而协方差矩阵对角线也全为1，导致原始指标信息差异性趋于一致，从而也消除了原始数据量纲和数量级在变异程度上对主成分的影响，不能准确表现评价指标全部所有信息。因此，对原始数据采用均值法进行处理改进，既消除了指标间量纲反应，也保留了指标的差异性。主要步骤：

原始数据均值化处理：

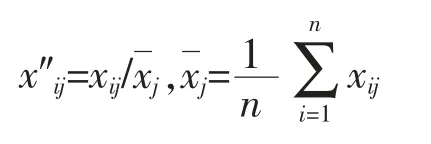
均值化后矩阵：A=（Aij）

处理后的原始数据协方差矩阵对角线数值公式计算：

式中 E（X）为x的均值；Var（X）为x的方差，此值能反映出评价指标之间在离散程度上的变异性，又不会丢掉指标之间的相关性，得到的相关系数矩阵充分体现了评价指标的全部信息量，因此对传统的主成分分析法进行均值化改进，处理消除指标间量纲影响，保留全部信息的方法是可行的。

2 研究概况与数据来源

2.1 研究概况

湖北省地处亚热带，国土总面积18.59万km2，占全国总面积的1.94%。全省大部分为亚热带季风性湿润气候，年平均气温15～17 ℃，降水充沛，降水地域分布呈由南向北递减趋势，截止2017年［12］，全省平均降水量1309.5mm，比常年偏多11.0%。全省水资源总量为1248.76亿m3，较上年减少16.6%，人均水资源总量为2116m3，较上年减少16.9%，亩均水资源总量较上年减少18.9%。在全省总用水量中，农业用水、工业用水和生活用水比例为2.46∶1.5∶1，耗水率43.1%。水质与水功能区达标方面，水功能去达标率86.6%，Ⅲ类水和Ⅲ类水以上河长占总评价河长的91%，劣Ⅲ类水主要超标项目为氨氮、总磷、高锰酸钾指数等指标，总而言之，湖北省水资源纵向分布特征与区域水资源分布特征基本一致。

2.2 数据来源与分析

研究中数据主要是来源 《湖北省统计年鉴》（2014～2018）、《湖北省环境质量状况公报》（2013～2017）、《湖北省水资源公报》（2013～2017） 及部分参考文献，其中有些指标值是通过计算综合获得。

根据评价指标选取原则，考虑湖北省具体实际情况，人均水资源量、供水量、人口总数等指标具有很重要的参考性和代表性，根据全国平均水平，人均水资源量2220m3/人，湖北省多年平均人均水资源量1866.6m3/人，低于全国平均水平15.9%。同时，湖北省供水量由2013年291.8m3到2017年290.26m3波动变化，最大与最小变化幅度相差6.8%，人口总数由2013年到2017年逐年递增，以每年0.3%比例增长。

3 水资源承载力评价指标体系构建

水资源评价指标体系的建立包含两层含义，一是水资源供水与需水总量平衡作为承载力评价标准；二是根据区域或低于特性，选取具有代表区域或者地域的影响因子作为评价指标，构建综合评价指标体系。水资源供需平衡能够简单便捷的反映供用关系，但无法反映各系统之间反映水资源承载力的错综复杂关系。具有代表性影响因素的选取既能反映出复杂的综合信息，又能体现出区域的发展特点和地域的资源特征，来建立具有本区域特色的评价指标体系。

考虑湖北省水资源总量多、开发利用率高和覆盖指标全面，避免选取指标重复性，构建多层次多系统的评价指标体系，具体指标体系如图1。

4 评价指标

4.1 改进主成分分析

通过改进主成分分析法，对影响因素在不同水平年的原始数据为基础计算对象，进而选择14个评价指标进行分析。

（1）原始数据均值化处理。

（2）计算协方差矩阵。

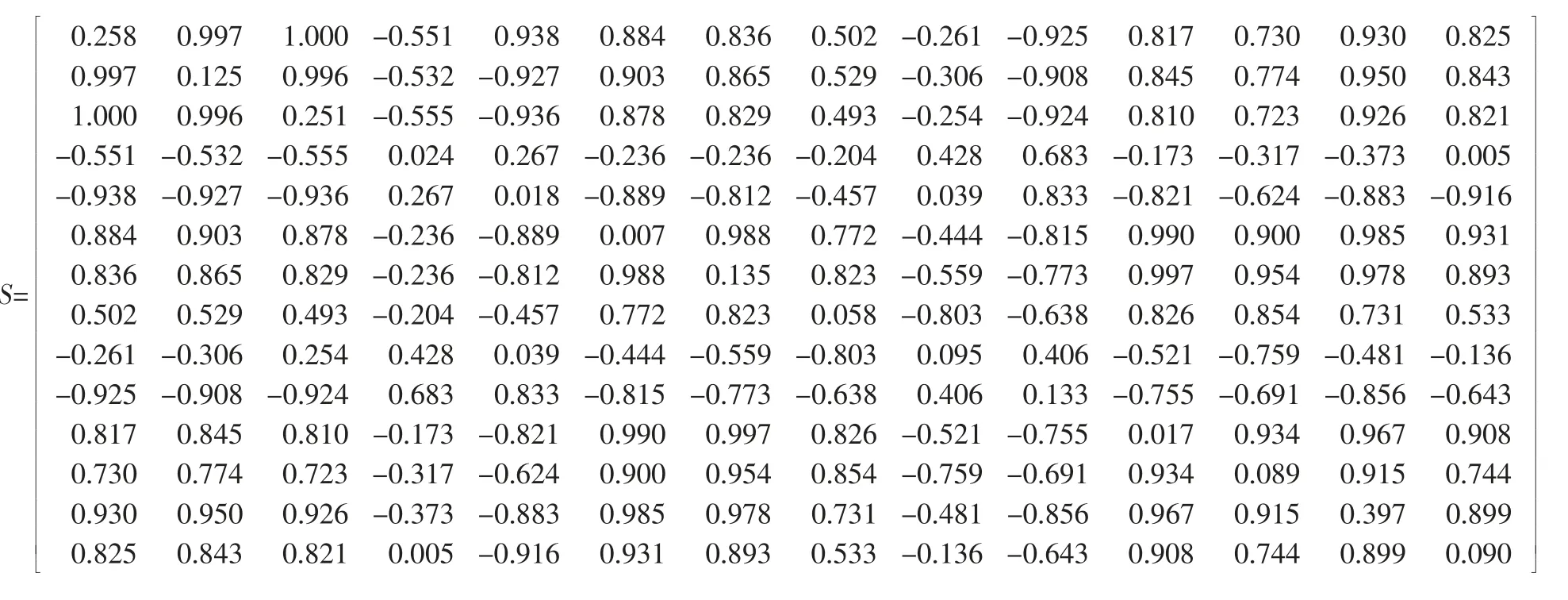
（3） 通过传统主成分分析法与改进主成分分析法分别计算主成分特征值和贡献率，并进行比较，结果如表1。

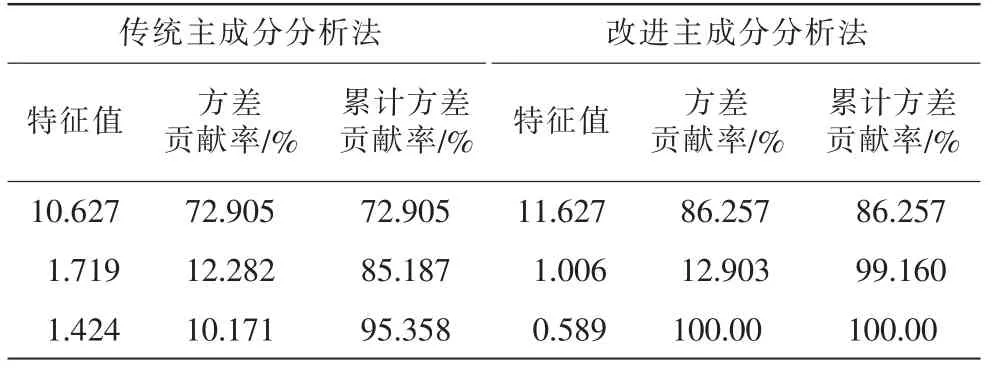
表1 传统主成分与改进主成分贡献率

根据表1计算结果，传统主成分与改进主成分累计贡献率相比较，主成分个数由3个变成2个，算法改进后在选取2个主成分时累计贡献率就达99.160%，说明方法改进在计算构造上起很大的降维作用，同时第1主成分累计贡献率由72.905%提升至86.257%，说明在进行方法改进后保留了大量评价指标的全部原始信息和差异变化，效果明显，为后续分析水资源承载力特殊影响因素提高计算效率。

4.2 水资源承载力综合评价分析

从主成分中载荷矩阵中可看出水资源总量、人均水资源量、降水量与第一主成分有很大正相关，相关系数分别为0.940，0.955，0.936，说明第一主成分主要代表着水资源系统变化； 万元工业增加值用水量和农田灌溉亩均用水量具有很大的负相关，相关系数为-0.489，-0.895； 因此主要体现社会经济发展工业和农业用水量的变化与水资源之间关系，通过算法改进，在确定的2个主成分所包含指标信息量能反映出复杂的综合信息，因此说明湖北省水资源改进主成分分析算法比传统算法更具有合理性。

在改进算法分析中，考虑到2个主成分，既累计频率达99.160%以上，涵盖了所选取评价指标值的全部信息，根据特征值计算得到指标载荷矩阵，得到相对应的2个主成分得分计算式：

通过变异系数法计算各个评价指标权重值得：（0.012，0.005，0.033，0.024，0.311，0.038，0.034，0.125，0.011，0.109，0.008，0.058，0.025，0.208）。以确定各主成分的特征值与所提取主成分特征值之和的比值作为权重，即各主成分的方差贡献率。

根据表1计算结果得知，对应三大主因子权重分别为：K1=0.8626，K2=0.1290，计算主成分综合评价指数P=0.8626P1+0.1290P2，可以得到云南省2013~2017年水资源承载力综合评价结果，如表2。

表2 云南省水资源承载力综合评价结果

根据表2结果可知，选取近5年的水资源承载力综合评价值有正值与负值，正负值说明的是承载力相对水平状态，并不是代表真实状况，综合评价结果越大，说明水资源承载能力越大，反之能力越小。湖北省从2013年开始水资源承载力逐年出现上升趋势，在2016年达到峰值2.928，随后略有下降，因在2016年降水量较大，处于丰水年份，地表水资源量和地下水资源量比往前偏多，比常年偏多44.6%。随着全省经济的快速发展，工业用水成逐渐上升，在用水总量中，工业用水达91.41亿m3，占32.4%，全省平均万元国内生产总值用水量87m3，万元工业增加值用水量为75m3，比上年减少13.7%，耗水率也由上年43%下降至42.5%，确实表明了在2016年水资源承载力出现小的波动变化。

为验证改进主成分算法结果的正确性，通过方差分析对均值化数据进行结果处理，结果如表3。

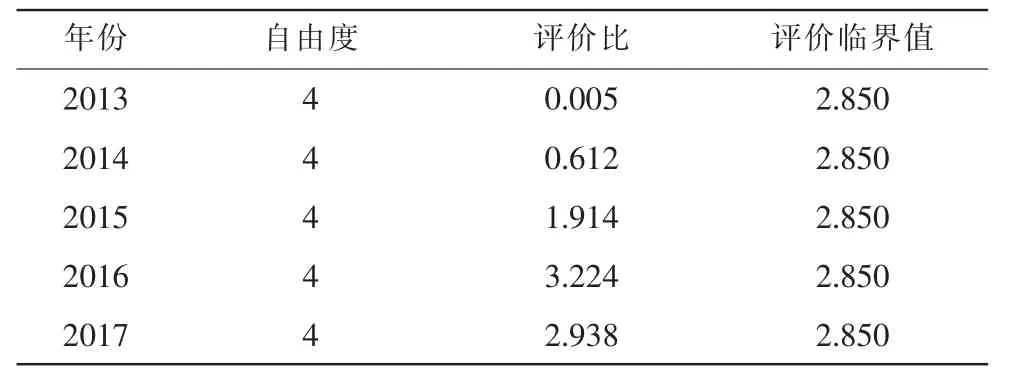
表3 改进算法后方差分析

由表3可知，在显著水平为0.05的条件下，评价指标在各水平年中的影响程度排序为2016，2017，2015，2014，2013年。与改进主成分分析法计算分析结果保持一致，说明了对原始数据进行改进算法运用到水资源承载力计算中是合理可靠的。

5 结语

（1）通过评价指标间因素分析，采用一种科学有效的方法减少评价指标之间的差异性，从而提高计算效率。

（2）改进主成分分析法充分考虑了指标间的相关性和差异性，较少在指标选取中主观因素的干扰，进一步提高了评价结果的准确性。

（3）改进主成分分析法是在原数据标准化的基础上进行改算，在考虑指标间量纲因素影响下，利用协方差矩阵代替相关系数矩阵，既避险了量纲之间的不统一性，又包含了评价指标的所有复杂综合信息，同时有效提高主成分因子，达到较早的降维效果，提高模型的计算效率。