液氧煤油发动机碟形金属密封特性

雷 征，陈 赟，雷博娟，陈建华

(西安航天动力研究所，陕西 西安 710100)

0 引言

相对于常规推进剂液体发动机，液氧煤油发动机的推力室工作压力更高，氧系统推进剂温度更低，而且燃烧后产生的高温燃气为富氧[1]。在这种高压、富氧和极端温度环境下，金属O形密封[2-5]、金属球头喇叭口密封[6-9]基本不能再用[10]。为解决1 200 kN推力液氧煤油发动机氧系统的低温、高压密封问题和燃气系统的高温、高压密封问题，设计了一种新型强制型碟形金属密封结构(简称碟形密封)，如图1所示。液氧煤油发动机目前使用的碟形密封结构有两种型式，大直径管路一般选用螺栓-法兰型密封结构，小直径管路一般选用外套螺母-台阶接头型密封结构。

图1 碟形密封Fig.1 Dish-shaped metal seal structure

碟形密封具有以下特点：

1)既适用于低温、高压管路密封，也适用于高温、高压管路密封；

2)密封环结构上酷似碟形弹簧，截面形状为平行四边形；

3)密封环内外两侧各有一个倒角，倒角两侧各形成一道密封面；

4)既能承受轴向载荷，也能承受径向载荷；

5)补偿安装偏斜的能力差，对装配精度的要求高。

采用非线性弹塑性有限元分析方法，选取1 200 kN推力液氧煤油发动机燃气系统使用的螺栓-法兰连接型碟形密封结构，研究其密封机理和轴向刚度特性。

1 问题简化

在简化模型时，提出以下几点假设[11]：

1)不考虑表面粗糙度等因素的影响，密封面是绝对光滑的；

2)不考虑产品的加工误差和装配偏差；

3)预紧力为将拧紧力矩等效转换后的轴向位移载荷；

4)施加边界条件时忽略实际工作过程中的振动情况。

2 非线性有限元弹塑性仿真模型

考虑到碟形密封的几何形状和约束条件具有轴对称性，加载过程中产生的位移、应变和应力同样具有轴对称性，为简化模型和减少数值计算工作量，仿真分析时选用二维轴对称有限元模型。

2.1 材料模型

碟形环材料为高温合金GH3044，法兰材料为高温合金GH202，材料性能如表1所示。在建立材料模型时，认为材料本构关系满足连续性、均匀性等假设条件[12]。在进一步建立高温合金GH3044和高温合金GH202的多线性等向强化模型时，应用了幂指数硬化理论和米塞斯屈服准则[13-14]。

表1 高温合金GH3044及GH202力学性能

2.2 单元类型

建模时考虑了介质温度对密封的影响，因此选用4节点热耦合轴对称四边形单元CAX4RT。该单元是一种温度和位移的耦合单元，包含了线性减缩单元的优点，又考虑了温度自由度，可用于静力分析及动态分析。

2.3 网格划分

网格划分采用自由网格划分技术和进阶算法，对密封面上的网格进行了加密处理。为消除网格密度对仿真结果的影响，进行了网格密度收敛性检查[15]，结果如图2所示。为了保证数值计算结果收敛，须使密封面上的相对网格密度达到400%，即网格尺寸不大于0.01 mm。

图2 网格密度收敛性检查结果Fig.2 Test results of mesh density convergence

2.4 接触设置

密封面之间的相互接触作用定义为表面与表面接触，密封面之间的相对滑动采用有限滑移算法进行表征，密封面之间的法向行为采用硬接触模型进行表征，切向行为采用滑动库伦摩擦模型进行表征，摩擦系数定义为0.15[16-17]。

2.5 边界条件

为模拟力学边界条件，对下法兰的轴向自由度、径向自由度及上法兰的径向自由度进行约束；为模拟热边界条件，在结构外壁面等效当量对流换热系数，在上、下法兰之间的间隙部位等效当量导热系数，在法兰和碟形环接触部位等效接触热导；将管路两端等效成绝热边界条件(q=0)[18]。如图3所示。

2.6 载荷步

工作时介质的温度载荷和压力载荷是同时作用的，建立弹塑性有限元模型时需要对两种载荷进行解耦，以降低非线性数值计算难度。结合碟形密封的实际工作过程，将密封结构的加载过程分解为4个步骤：

载荷步1：初始接触，在上法兰顶端施加微小轴向位移载荷U2为0.001 mm；

载荷步2：实现预紧，将轴向位移载荷U2增加至1.455 mm；

载荷步3：施加内压，在管路内壁面施加压力载荷为19.37 MPa；

载荷步4：施加温度，在管路内壁面施加第一类边界条件T=348.00 ℃，同时对轴向位移载荷进行补偿，将轴向位移载荷U2减少至1.283 mm。

图3 边界条件Fig.3 Boundary conditions

按照图4所示位移-时间曲线施加轴向位移载荷。S0为碟形密封处于初始安装状态；S1为碟形密封处于初始接触状态；S2为碟形密封处于预紧状态；S3为碟形密封处于内压作用状态；S4为碟形密封处于工作状态。

图4 位移-时间曲线Fig.4 Variation of displacement with time

3 密封机理及轴向刚度特性

碟形密封各密封面的密封面积、密封应力随加载时间的变化规律如图5所示，预紧过程中作用于密封结构的轴向压紧力随位移的变化规律如图6所示。

图5 密封面积和密封应力随加载时间的变化规律Fig.5 Variations of sealing area and sealing stress with time

图6 轴向压紧力-位移曲线Fig.6 Variation of axial pressing force with displacement

3.1 预紧状态

从S0到S1，轴向位移载荷U2由0 mm增加至0.001 mm。在此预紧载荷作用下，碟形环所受轴向压紧力由0 N增加至195.8 N，各密封面均产生微弱接触作用，碟形密封结构所受轴向力随位移增加而增大，轴向刚度约为3.29×105N/mm。

从S1到S2，轴向位移载荷U2由0.001 mm增加至1.455 mm，各密封面的密封面积、密封应力及密封环所受轴向压紧力的变化可分为3个阶段：

1)轴向位移载荷U2=0.001～0.582 mm。碟形环所受轴向压紧力、各密封面的密封面积和密封应力随着位移载荷的增加而增大，当位移载荷增加至0.582 mm时，轴向压紧力达到峰值50 874.0 N，如图6中a点所示。碟形密封结构所受轴向压紧力先随位移增加快速增大，随后增速减缓，表明碟形密封结构刚度在该阶段加载过程中呈现减小的趋势，加载至a点时轴向刚度减小至约138 kN/mm，说明碟形金属密封出现轴向失稳现象。

2)轴向位移载荷U2=0.582～1.309 mm。随着位移载荷的增加，各密封面的密封面积以及密封面A，C的密封应力继续增大，碟形环所受轴向压紧力和密封面B，D的密封应力开始减小，当位移载荷达到1.309 1 mm时，轴向压紧力降至39 692.4 N。在此阶段，碟形环出现“S”形变形，如图7所示。碟形密封结构的轴向刚度由“正”突变为“负”，约为-18 kN/mm，如图6中ab段所示，说明碟形环发生了明显轴向失稳。

图7 碟形环出现“S”形变形Fig.7 S-shaped deformation of dish-shaped metal ring

3)轴向位移载荷U2=1.309～1.455 mm。从图6中b点开始，碟形环所受轴向压紧力再次增大，这是由于在E处产生新的接触对后结构刚度增加所致，如图8所示。当位移载荷达到1.455 mm时，轴向压紧力迅速增大至88 579.9 N，该阶段碟形密封结构轴向刚度约为340 kN/mm，与初始阶段(图6中S0S1段)轴向刚度基本相当，说明结构进入后屈曲阶段。密封面A，B，D的密封面积和密封面C的密封应力继续增大，密封面C的密封面积和密封面A，B，D的密封应力减小。

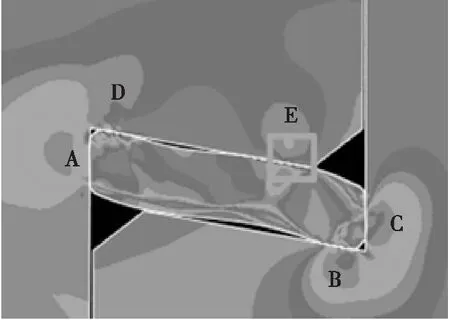
图8 密封面E接触Fig.8 Contact action of sealing surface E

3.2 工作状态

从S2到S3，碟形密封的轴向位移载荷U2保持不变。在介质压力产生的轴向分离载荷作用下，碟形环所受轴向压紧力、密封面积、密封应力出现微小变化。轴向压紧力由88 579.9 N增大至92 157.0 N，增加了4.02%。各密封面的密封面积和密封应力变化情况如表2所示，分析可知：

1)内压载荷对密封面B的密封面积和密封应力影响最大，对密封面A的密封面积和密封应力影响最小。

2)在内压载荷作用下，密封面B的密封面积减小，密封面D的密封面积增大；密封面A，B，C的密封应力减小，密封面D的密封应力增大。

表2 施加内压载荷后各接触面密封面积和密封应力变化情况

Tab.2 Variations of sealing area and sealing stressof each contact surface after applying inter-nalpressure load%

密封面ABCD密封面积变化情况0.00-5.780.002.20密封应力变化情况-0.47-8.36-2.781.21

从S3到S4，轴向位移载荷U2由1.455 mm减小至1.283 mm，碟形环所受轴向压紧力由92 157.0 N减小至52 322.5 N，减小了43.23%。各密封面的密封面积和密封应力变化情况见表3，分析可知：

1)温度载荷对密封面C的密封面积和密封面D的密封应力影响最大，对密封面B的密封面积和密封面A的密封应力影响最小。

2)在温度载荷作用下，各密封面的密封面积均增大，密封应力均减小。

表3 施加温度载荷后各接触面密封面积和密封应力变化情况

Tab.3 Variations of sealing area and sealing stressof each contact surface after applying tem-perature load%

密封面ABCD密封面积变化情况8.143.8216.630.84密封应力变化情况-5.34-16.78-9.20-48.78

3.3 仿真结果分析

由以上研究可知：

1)轴向位移载荷作用后，结构中不仅产生了轴向压紧力，而且产生了径向压紧力，轴向密封面B，D和径向密封面A，C均形成了一定的密封面积和密封应力。

2)预紧状态下，碟形环上的4个密封面均发生塑性变形，且最大等效塑性应变出现在密封面A；预紧过程中，碟形密封环整体塑性变形较大且出现明显的“S”形变形；碟形密封结构轴向刚度先减小后变负，结构出现失稳现象，当新密封面E形成后轴向刚度再次转为正刚度，刚度值与初始阶段基本相当。

3)工作状态下，介质压力载荷和温度载荷作用后，各密封面的密封应力降低，密封面D的密封应力降幅甚至达到50%，但各密封面的密封面积有所增加，整体密封效果仍然较好，没有出现密封失效现象。

4 结论

以1 200 kN推力液氧煤油发动机燃气系统使用的螺栓-法兰连接型碟形金属密封结构为研究对象，构建了该密封结构的弹塑性有限元仿真模型并进行了非线性数值仿真计算。通过分析有限元仿真结果，得到了碟形密封的密封机理和轴向刚度特性，结论如下：

1)采用非线性有限元弹塑性仿真方法可以对碟形密封的作用过程、密封机理及轴向刚度特性进行定量分析和研究。

2)预紧载荷作用后，碟形密封结构中同时产生轴向压紧力和径向压紧力，4个密封面产生一定的密封面积和密封应力。

3)预紧状态下，碟形环的4个密封面均发生塑性屈服，密封环整体塑性变形较大且出现“S”形变形；碟形密封结构轴向刚度先减小后变负，结构出现失稳现象，当新密封面E形成后轴向刚度再次转为正刚度。

4)工作状态下，介质压力载荷和温度载荷使得各密封面的密封性能略有下降，结构未出现密封失效现象。