姿控动力系统连接螺钉振动疲劳仿真分析研究

薛 杰，王 伟，杜大华，隋禄涛

(液体火箭发动机技术重点实验室，陕西 西安 710100)

0 引言

随着现代工业的发展，结构在力学环境中出现的振动断裂问题越来越多，特别是航空航天、化工、兵器及船舶等工程领域，振动环境对结构带来的影响更为突出。而为了确保产品结构安全、可靠运行，目前往往需要通过随机振动试验来考核力学环境下结构的适应性或从中寻找结构的薄弱环节。但是，一方面由于振动试验工作周期长、试验设备及保障成本高;另一方面，振动试验难于定量地给出被试结构在试验中产生的疲劳损伤，尤其是各种连接件根部的细小位置处。因此，能够运用仿真技术进行结构振动试验的模拟并进行振动疲劳损伤的有效估算就显得格外重要。

自1985年Turan Dirlik发表他的博士论文[1]以来，国外对振动疲劳的研究已从理论逐步走向工程应用，国内学者在这一领域也做了很多工作，其中，文献[2-9]分别对不同结构在随机振动环境下进行疲劳损伤的研究，均取得了较好的效果，说明了Dirlik方法的可行性及有效性。本文在该方法的基础上，通过单阶模态响应，对某姿控动力系统在随机振动试验中发生疲劳断裂的连接螺钉进行损伤分析，为结构改进提供一定的参考。

1 振动疲劳寿命估算方法

1.1 材料疲劳性能描述

目前，描述金属材料疲劳性能的主要方式包括应力寿命(s-N)曲线及应变寿命(ε-N)曲线。其中，s-N曲线通常用于高周疲劳分析，ε-N曲线则用于低周疲劳分析。由于幂函数公式描述材料的疲劳属性为

sb·N=C

(1)

式中:b，C为材料寿命参数，通过对上式两边取对数，可以发现在双对数坐标下s与N的关系变成一条直线，与一般金属相应的高周疲劳曲线基本一致。因此，在本文研究的结构高周振动疲劳问题中适合采用式(1)进行分析。

1.2 振动应力应变历程算法

对于稳态随机振动过程，通常运用统计的方法对相应结构应力应变历程进行描述，而在振动疲劳分析中比较成功的描述方法为Dirlik法。

在文献[1]中，Dirlik法通过对70种不同分布形状的功率谱函数进行模拟分析，所模拟的功率谱函数的不规则因子γ的变化范围从0.16～0.99，适用于宽带及窄带的情况，最终得到其雨流循环幅值概率密度函数的经验公式。Dirlik公式由一个指数函数、带瑞利参数的瑞利函数及标准瑞利函数共同组成[10]

(2)

其中

D3=1-D1-D2

式中：Z为正则化幅值；s为应力幅值；P(s)为应力雨流循环的幅值概率密度函数；m0，m1，m2，m4分别为应力响应功率谱密度函数的零阶矩、一阶矩、二阶矩及四阶矩。与部分文献不同的是，式(2)中采用应力幅值概率密度函数而不是应力范围概率密度函数，是因为本文采用的s-N曲线中s指的是应力幅值而不是应力范围，二者为两倍关系

(3)

式中：mi为功率谱的i阶矩；f为频率；G(f)为应力单边功率谱。

1.3 疲劳累积损伤理论

疲劳累积损伤目前存在多种理论，其中Palmgren-Miner线性累积损伤理论是最经典、应用最为广泛的一种。该理论认为结构在经历多级应力循环后产生的损伤量为

(4)

式中：ni为对应当前应力水平si下的实际循环数；Ni为材料应力幅值为si时的疲劳寿命。

而ni，Ni可表示为

ni=E(P)·T·P(si)·Δsi

(5)

(6)

将式(5)、式(6)代入式(4)，并把求和换成积分得到

(7)

当结构某位置的损伤量D=1时，认为结构该位置发生疲劳破坏，由此推出结构的疲劳寿命

(8)

2 姿控系统连接螺钉计算模型

某姿控动力系统在经历y向随机振动试验(5 min)后，经检查未发现异常，继续完成z向随机振动试验(5 min)，直到该试验结束后才发现连接螺钉出现了疲劳断裂，如图1所示。

图1 振动断裂的螺钉结构Fig.1 The broken screw in vibration

该姿控动力系统主要包括贮箱、气瓶、框架、底板及连接螺钉，连接螺钉起到框架与底板的连接作用，模型如图2所示，其中，坐标系以推力方向为x向，框架上端长边法兰为z向，按右手准则确定y向。试验中，振动激励由振动台通过试验工装传到框架法兰及底板外侧，因此，随机振动加速度激励加载于此。各组件材料及其力学性能参数如表1所示。

3 结构模态仿真结果

通过y、z方向10～2 000 Hz范围的频响分析可知，结构响应主要出现在500 Hz以下。因此，重点分析500 Hz以下姿控动力系统的模态[11]，计算得到振动试验状态下结构的前9阶模态频率及模态振型，如表2所示。

图2 姿控动力系统结构有限元模型 Fig.2 The finite element model of DACS

组件材料密度/(kg·m3)弹性模量/MPa泊松比底板30CrMnSiA7 750196 0000.300框架2A142 80070 0000.330气瓶、贮箱TC44 400109 0000.340螺钉30CrMoA7 870218 0000.286

表2 振动试验状态姿控动力系统模态计算结果

Tab.2 Modal calculation results of the DACS in the vibration test state

阶数模态频率/Hz振型概述1216.5框架整体y向摆动2243.3框架、贮箱、气瓶整体摆动3339.3气瓶横向(z方向)摆动4356.9气瓶及框架下端反向摆动5372.3气瓶上下运动、框架下端横向摆动6393.3气瓶、框架及贮箱作横向复杂摆动7423.0框架中部与气瓶横向同摆8477.7框架下端z向摆动9558.4框架、气瓶整体扭转摆动

为了解哪些模态在随机振动环境下会对连接螺钉产生较大的应力，分别提取前9阶模态单独产生的结构应力响应及全模态应力响应，并基于第1节介绍的振动疲劳寿命估算方法分别进行损伤计算与分析，结构系统模态振型如图3～图5所示。

图3 结构系统前3阶模态振型Fig.3 The first three modal shapes of the structure model

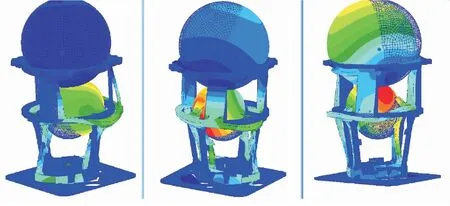
图4 结构系统第4至第6阶模态振型Fig.4 The fourth to sixth modal shapes of the structure model

图5 结构系统第7至第9阶模态振型Fig.5 The seventh to ninth modal shapes of the structure model

4 随机振动疲劳损伤计算

为了得到全模态及各阶单模态在振动试验环境下对连接螺钉产生的损伤，首先需要得到振动激励条件下全模态及各阶单模态引起的应力功率谱密度函数，这可通过有限元求解器Nastran进行模态法频域响应及随机振动的计算获得[12-13]。计算中，各阶模态阻尼采用0.03，随机振动输入条件如图6所示，试验仿真分两个方向(y、z)，每个方向5 min。

图6 随机振动试验条件Fig.6 Random vibration test input condition

经过计算，得到结构分别在y，z随机振动环境下连接螺钉断裂位置的应力功率谱密度函数，如图7、图8及图9所示，其中，y向随机振动中连接螺钉断裂位置附近应力RMS值分布如图10所示。实际结构工作过程或振动试验通常均表现为多轴应力问题，而目前求解多轴疲劳问题的一类方法是将多轴应力问题等效为单轴应力问题[14-17]。根据计算出的应力功率谱，应用式(7)和式(8)得到相应的损伤量D及寿命Ts，结果如表3所示。其中，参数m，C通过对材料应力寿命数据的拟合得到，m=13.9、C=7×1 043。另外，表3中总寿命计算结果表示姿控动力系统经历了391.9 s的y向随机振动后，再经历391.9 s的z向随机振动，连接螺钉就发生结构疲劳断裂。

计算结果表示：在经历连续两个方向的随机振动试验后，姿控动力系统连接螺钉断裂位置处的疲劳损伤量D达到0.765 4，距离理论上结构发生疲劳破坏时D=1存在一定出入，分析的主要原因为：文中采用的振动疲劳寿命评估方法本身具有统计特性，个例结果具有一定的散差。

图7 y向随机振动单阶模态应力响应功率谱密度曲线Fig.7 The stress power spectral of single mode response in the y direction random test

图8 z向随机振动单阶模态应力响应功率谱密度曲线Fig.8 The stress power spectral of single mode response in the z direction random test

图9 随机振动中全模态应力响应功率谱密度曲线 Fig.9 The stress power spectral of full mode response in the random test

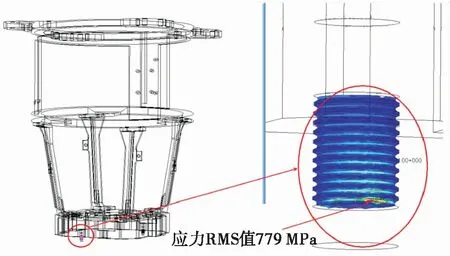
图10 y向随机振动中连接螺钉断裂位置应力RMS值分布 Fig.10 The stress RMS distribution of the broken screw during y direction random test

另外，不同方向的随机振动，各阶模态对螺钉振动断裂的影响大小不一样，其中，y向随机振动中第1阶模态产生的损伤较大，而z向随机振动中第3阶、第8阶模态影响更大，因此，在后续的防护和结构改进中应重点关注以上3阶模态。

从表3的应力RMS值与损伤量的对应关系来看，较大的应力RMS值通常也会产生较大的疲劳损伤量，因此，工程上常依据仿真得到的应力RMS值的相对大小来定性地评估结构在随机振动试验中的危险部位[18]。其实，这并不充分，如y向随机振动中第1阶模态产生的应力RMS值比z向随机振动中第8阶模态大，但损伤量却比较小。

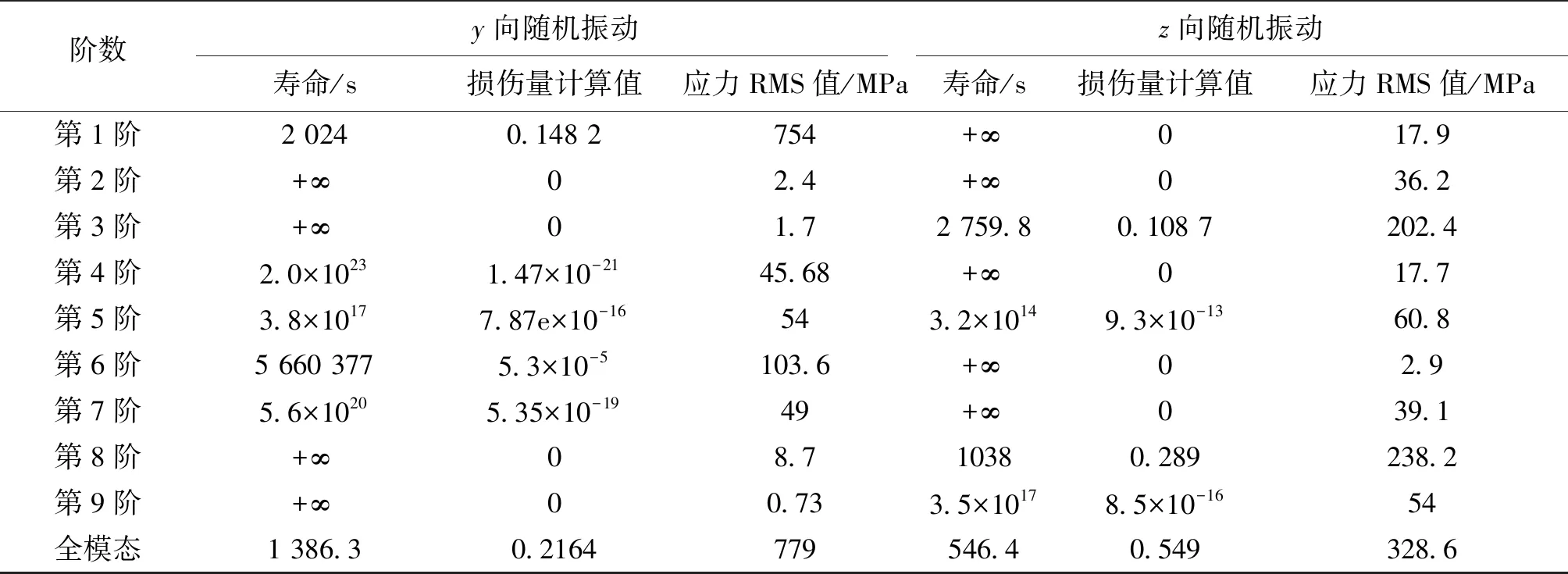
表3 随机振动环境下螺钉断裂位置疲劳损伤量及寿命计算结果

5 结论

通过仿真分析可以得到以下主要结论：

1)在经历连续两个方向的随机振动试验后，姿控动力系统连接螺钉断裂位置处的疲劳损伤量D达到0.765 4，虽然离D=1存在一定距离，但仍是一个比较大的损伤量，与试验结束后螺钉疲劳断裂的现象基本吻合。

2)通过单阶模态响应的损伤量计算，可以得到各阶模态对结构振动疲劳断裂的影响大小，从而找出影响较大的部分模态，为结构改进及抗疲劳设计提供参考。

3)仅仅依靠应力RMS值的相对大小来评估结构在随机振动试验中的危险部位是不充分的，更好的做法是把具有较大应力RMS值的位置都进行疲劳损伤量计算，再根据计算结果进行定量评估。