铝合金人行天桥人群荷载动力特性研究

张泰源，宋郁民，孟雨泽

(上海工程技术大学 城市轨道交通学院， 上海 201620)

近年来，因为铝合金结构自重轻、耐腐蚀、强度高、韧性好、易于吊装与经济性好的特点，铝合金在人行天桥中的应用越来越多。自2000年伦敦千禧桥事件之后，人行桥的人致振动问题引起了广泛的关注，相比其他桥梁而言，人行天桥更容易在人群荷载下出现大幅度振动问题，铝合金天桥因其自重相对较小，所以人群荷载的振动影响更为显著[1-6]，但国内的人行桥设计，基本上是采用铁路桥或公路桥规范的动力冲击系数的概念, 将其处理为静力等效问题来考虑，这与实际情况有所出入。本文以某新建30 m的铝合金桁架人行天桥的设计为工程背景，在进行动力设计分析时，研究在行人以不同速度与不同方向通过人行天桥时天桥的最大动力响应，并对天桥进行舒适度评价。

1 工程概况

新建天桥采用单孔桁架结构形式，设计安全等级为一级，环境类别为Ⅱ类，地震峰值加速度0.20g，上部采用铝合金桁架式结构，主桥采用跨径30 m跨简支铝合金桁架桥，桁架一跨共12榀，每榀间距2.5 m。桥面总宽4.5 m，桁架结构高4 m,步道采用铝合金结构板。主桥桁架理论高度4 m，高跨比1/7.5。桥梁全长37 m，宽度为4.5 m，梯道宽度3.0 m，平立面设计图见图1、图2。

图1人行天桥立面图(单位：cm)

图2人行天桥截面图(单位：cm)

2 计算模型的建立

利用MIDAS/Civil建立天桥模型，天桥上部结构采用6082 T6铝合金材料，桁架上、下弦杆采用双槽钢截面，腹杆与横联采用箱型截面，全桥模型共由693个节点，1 070个梁单元，240个板单元组成，有限元模型见图3。

图3 MIDAS有限元模型

3 动力特性研究分析

首先对结构自振特性进行分析。全桥采用梁单元模拟铝合金桁架，桥面板采用板单元结构，模型建立后进行模态分析，得到结构前10阶自振频率如表1所示。

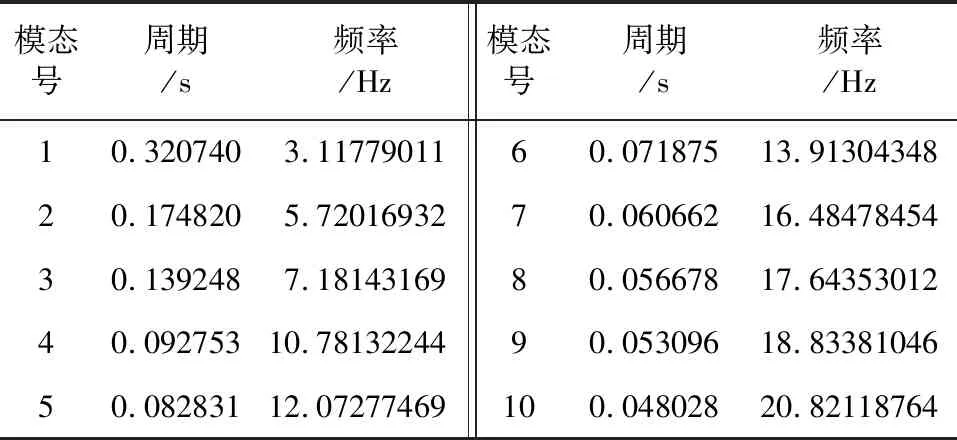
表1 人行天桥前10阶自振频率

本文结构动力特性分析仅考虑前10阶模态的参振作用。

3.1 行人竖向动力荷载模型

行人的竖向动力荷载采用Bachmann等[7]提出的竖向荷载公式，该式采用傅里叶级数形式，将行人的竖向荷载表示为人体自重G与若干谐波荷载之和，即：

(1)

式中：Fpv(t)为行人引起的竖向荷载；G为单个行人的重量；αnv为第n阶竖向荷载谐波的动载因子；fpv为行人竖向步频；Φnv为第n阶竖向荷载谐波相位角；t为时间；n为谐波阶数；k为对荷载贡献的总谐波数。

2001年，Yong[8]总结了诸多学者对人形荷载时程的测量结构，归纳出了前四阶行人竖向荷载动载因子计算公式，2012年谢伟平等[9]根据中国人的情况，总结了前四阶动载因子计算公式为：

(2)

以0.05 s作为时间步长，通过式(1)、式(2)建立1.5 m/s～5.0 m/s各速度梯度下的时程函数，以1.5 m/s、2.5 m/s、3.5 m/s、4.5 m/s为例，函数图像见图(4)—图(7)。

图4 1.5 m/s时程函数

图5 2.5 m/s时程函数

图6 3.5 m/s时程函数

图7 4.5m/s时程函数

由于人行桥的舒适性是行人的主观感受，影响因素十分复杂，国外对此已有相关规范，但国内相关规范只提出了天桥上部结构竖向自振频率≥3 Hz来避免共振问题，现大部分桥梁设计也是以此作为标准[10-14]。在2013年，袁爱民等[14]基于烦恼率进行了相关的研究。本文采用国际通用标准ISO10137[15]中的规范指标来进行人行天桥的舒适度评价，具体表达式如下：

(3)

式中：fv是结构振动的频率；alim是响应的峰值加速度，m/s2。

天桥的前10阶自振频率最小值为3.13 Hz，根据上式计算得峰值加速度alim=0.88 m/s2。

3.2 同速度同方向下人行天桥的动力响应

通过改变荷载系数以表现人数的不同，建立10人以1.5 m/s～5.0 m/s的速度沿天桥轴线同方向通过天桥的模型，来模拟行人以不同速度通过天桥时的动力响应，时程荷载工况分析方法选用振型叠加法，考虑振型数量为前10阶振型，特征值分析类型选用子空间迭代法，迭代次数为20次。人的体重一般取值为650 N～750 N，本文在计算中取G=700 N，步长取0.7 m，分析时间步长取0.01 s，以节点动力荷载形式添加对应时程函数，荷载模式见图8。

利用MIDAS/Civil在天桥模型无外荷载的情况下进行时程分析，查看人行天桥跨中处节点(56号节点)处的动力响应，结果见表2。

图8荷载模式

表2 同方向、速度梯度下56号节点动力响应

由表2可知，由于行人速度在2.0 m/s和2.5 m/s时，步频与结构自振频率3.13 Hz相近，所以56号节点的动力响应最为显著；随着行人速度的增加，在同方向同人数的情况下，节点最大加速度呈上升趋势。

3.3 同速度不同方向下人行天桥的动力响应

将10人分为两组，每组5人，分别从天桥两端以1.5 m/s～5.0 m/s的速度沿天桥轴线通过天桥，建立模型后查看56号节点处的动力响应，结果见表3。

表3 不同方向、速度梯度下56号节点动力响应

由表3可知，同表2一样，当步频与天桥自振频率相近时，56号节点的动力响应更为显著，而且最大加速度依然随着行人速度的增大而增大。但是与表1相比，在天桥上行人人数相同的情况下，双向行走工况下56号节点的动力响应要比单向行走工况下的动力响应要小，竖向挠度、速度、加速度几乎都有所降低。

3.4 不同速度同方向下人行天桥的动力响应

将10人分为两组，第一组6人以1.5 m/s的速度沿天桥轴线通过天桥，相隔3 s后，第二组4人以3 m/s的速度同方向通过天桥，建立模型后查看56号节点处的动力响应，结果见表4。

表4 不同速度同方向下56号节点动力响应

同表2相比，56号节点的动力响应介于10人分别以1.5 m/s和3.0 m/s通过天桥时的动力相应，但所得值并不是单纯的加权平均值，而是在此基础上有了一定的削弱，竖向最大挠度削弱了33%，最大速度削弱了27%，最大加速度削弱了13%。

3.5 不同速度不同方向下人行天桥的动力响应

将10人分为四组，第一组3人与第二组3人分别以1.5 m/s的速度沿天桥轴线从两端通过天桥，相隔3 s后，第三组2人与第四组2人分别以3 m/s的速度从两端通过天桥，建立模型后查看56号节点处的动力响应，结果见表5。

表5 不同速度不同方向下56号节点动力响应

同表3相比，56号节点的动力响应介于10人分别以1.5 m/s和3.0 m/s通过天桥时的动力响应，但所得值也不是简单的加权平均值，也是在此基础上有了一定的削弱，竖向最大挠度削弱了24%，最大速度削弱了26%，最大加速度削弱了5%。同表4相比，在天桥上行人人数相同的情况下，不同方向工况下56号节点的动力响应要比同方向工况下的动力响应要小，竖向挠度、速度、加速度也有所降低。

3.6 满载工况下人行天桥的动力响应

假定满载工况下，行人密度为1.5 人/m2，行人的行走速度为1.5 m/s，沿天桥横向方向，行人数量为6人，满载时，桥面人数为270人，行人行走方向为同向。建立模型后查看56号节点处的动力响应，结果见表6。

表6 满载工况下56号节点动力响应

由表6可知，虽然满载时行人数量较大，但是由于行走速度受到限制，导致56号节点处的动力响应并不高，最大加速度仅比表1中1.5 m/s行走速度工况大126.93 mm/s2。

4 结 语

(1) 随着行人速度的增加，在同方向同人数的情况下，节点最大加速度呈上升趋势，行人的步行频率越接近天桥的自振频率，动力响应越大。

(2) 在桥面行人数量相等的情况下，双向行走工况下的动力响应要比单向行走工况下的动力响应要小，竖向挠度、速度、加速度都有所降低。

(3) 行人同时以不同速度通过天桥时，所产生的动力响应介于以各单一速度通过天桥所产生的动力响应之间，其值略低于各单一速度动力响应的加权平均值。

(4) 发现在不同工况下结构的动力响应差距较大，建议在设计阶段应根据天桥的使用条件进行相应的计算讨论，在保证结构安全性能、避免共振的同时，也要满足行人舒适性的要求。