考虑过程阻尼的铣削稳定性分析

王田，于慎波，范季铮，梁赢东

(沈阳工业大学 机械工程学院，辽宁 沈阳 110870)

0 前言

机械加工中的颤振不仅会降低被加工表面质量和加工精度，而且严重时还会损坏刀具与机床[1]。在铣削加工中，颤振是国内外研究的热点。最早的机床颤振理论是由F.W.Taylor在20世纪初提出的，他认为颤振是由于切削频率与机床结构中某一部分的固有频率相同，产生共振所引起的[2]。1946年Arnold首次提出摩擦型颤振理论，他认为摩擦型颤振是由于切削过程中刀具与工件之间在切削速度方向上摩擦作用引起的[3]。T.R.Sisson指出切削过程中切削力与切削速度成反比是产生摩擦型颤振主要原因之一[4]。Peter Stelter将车刀简化成悬臂梁模型，指出其在受到干摩擦力作用时会发生摩擦型颤振[5]。1954年J.Tlusty首次提出振型耦合型颤振，他指出振动系统在两个自由度方向上刚度接近时，产生耦合效应从而导致振型耦合型颤振发生[6]。于俊一等通过考虑耦合效应、耦合效应与再生效应的综合作用，指出机床工艺系统刚度主轴的最佳方位与动态切削力的构成有关[7]。Gasparetto通过建立耦合型颤振模型，分析刀具在切削过程中的运动轨迹，得出了切削的稳定性条件[8]。R.S.Hahn在1954年提出再生型颤振理论，他指出在有振纹的工件表面上进行切削从而引起振纹再生效应，当满足颤振产生的条件时，就会产生再生型颤振[9]。在此理论基础上，J.Tlusty和S.A.Tobias在同年指出再生型颤振中的动态切削深度与动态切削力会相互影响,并通过绘制颤振稳定性叶瓣图分析了切削加工系统在某一切深下的稳定性[10,11]。后来有实验表明，低速切削加工时，过程阻尼可提高切削稳定性极限，即抑制了颤振。过程阻尼的分析和建模是近年国际学术界的研究热点[12,13]。Altintas 等将其列为尚未解决的切削颤振中的难点[14]。

Sisson和Kegg等最早注意到低速下工件切削表面和刀具后刀面接触是阻尼增加的主要原因[15]。李忠群等以考虑过程阻尼的单自由度车削和二自由度铣削稳定性建模分析为基础，实现颤振稳定性的预测[16]。Tyler等将表面法线方向的过程阻尼力描述为切削深度、切削速度、刀具进给速度和单一经验系数的函数,获得了多自由度的动力学系统[17]。Li和Sun等在高阶时域算法中把再生效应、螺旋角和过程阻尼引入到铣削系统扩展动力学模型中，保证了计算效率和精度[18]。李钟昀运用柯西变换改进了二阶半离散法，采用该方法和不动点理论预报了铣削稳定性与表面位置误差[19]。

本文在传统的铣削动力学基础上，建立了一种考虑过程阻尼的铣削动力学模型，得到了铣削加工的稳定性叶瓣图。实验结果表明，利用考虑过程阻尼的铣削动力学方程得到的稳定性叶瓣图，比未考虑过程阻尼得到的稳定性叶瓣图精度更高，在低速区，稳定性区域显著增加。

1 过程阻尼

在铣削加工中，如果颤振发生，振幅增大。当铣削刀具后刀面和工件加工表面之间存在相互作用时，产生过程阻尼。该阻尼增加了铣削稳定性，特别是在低切削速度下，会对颤振产生抑制作用。图1描述了过程阻尼机理。

图1 过程阻尼的描述示意图

当每个刀齿从被加工工件波纹表面移除切屑时，在1点和3点之间产生过程阻尼力。人们普遍认为，过程阻尼取决于刀具后刀面与工件接触压力和刀具后刀面压入工件的体积。例如2点，后刀面与工件表面切向夹角逐渐减小为负值，压入体积逐渐增大，干涉作用逐渐增强，这直接导致过程阻尼力的产生。然而，在点4，当刀具在被加工工件波纹表面上向上移动时，干涉消失。Ahmadi和Ismail等[8]指出过程阻尼可以用等效粘性阻尼表示为：

(1)

式中，Ksp为压痕系数，W为刀具后刀面的磨损带宽度，a为轴向切削深度，v为切向速度v=πDΩ/60，D表示刀具直径。

2 考虑过程阻尼的铣削稳定域预测

在二自由度铣削系统中，考虑过程阻尼的铣削动力学模型方程表示为

式(2)中切削力系数表达式为

过程阻尼力表达式为

将式(2)转换成状态空间表达式为

(3)

其中，M、C、K、q、H和G分别表示矩阵。

(4)

式中，矩阵A0为系统中时不变的常数项，矩阵A(t)和B(t)由动态切削力决定的周期性矩阵，满足A(t)=A(t+T)、B(t)=B(t+T)，T为时间周期且与时滞量相等。

A(t)=

(5)

Xk+1=[I-Fk+1]-1[(F0+F0，k)Xk
+Fm-1Xk+1-m+FmXk-m]

(6)

其中

F0=φ0

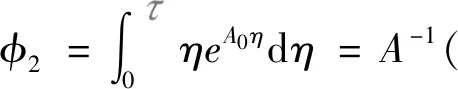
根据式(6)构造离散映射表达式

Yk+1=DkYk

(7)

其中Yk可表示为

Yk=[Xk,Xk-1,…,Xk+1-m,Xk-m]T

(8)

(9)

矩阵P、Pm-1和Pm分别为

P=[I-Fk+1]-1(F0+F0，k

Pm-1=[I-Fk+1]-1Fm-1

Pm=[I-Fk+1]-1Fm

一个完整周期的状态转移矩阵可以通过Dk构造出来。即

φ=Dm-1Dm-2…D1D0

(10)

最后，由Floquet理论可知，如果状态转移矩阵φ的所有特征值模均小于1，则系统稳定；否则系统处于不稳定状态。

3 试验分析与验证

铣削稳定性验证试验在某机床有限公司的G7-龙门式加工中心进行，测试系统如图2所示。所用铣刀型号为400R16R1006B32和刀片型号为APMT1604PDER-H2。刀具直径100 mm，刀具齿数为6。进行刀具结构实验模态分析时，采用B&K3050A型6通道数据采集系统；冲击力锤型号为B&K8207；加速度传感器B&K4508B。加工方式为铣槽，工件材料为45#钢，尺寸为400 mm×400mm×50mm。由槽铣快速标定法获得切向力系数Kt=827 MPa，径向力系数Kr=576 MPa，压痕系数Ksp=1.5×105N/mm3，库仑摩擦系数μ=0.3[8]。测得刀具的频响函数如图3所示。刀具模态参数见表1。

图2 铣削试验测试系统

图 3刀具的频响函数

表1 刀具系统模态参数

结合上述参数，利用Matlab编程计算，绘制出未考虑过程阻尼和考虑过程阻尼的稳定性叶瓣图，如图4所示。对比分析发现：与未考虑过程阻尼影响相比，考虑过程阻尼影响后低速区的稳定切削区域增加显著，在高度区稳定性叶瓣图几乎是一致的，这意味着在高速切削条件下，过程阻尼对稳定性叶瓣图的影响不明显。为了验证仿真结果的正确性，根据绘制的稳定性叶瓣图，选取考虑过程阻尼的稳定性叶瓣曲线以下A点(主轴转速为400 r/min、切削深度为1.5 mm)和以上B点(主轴转速为400 r/min、切削深度为2 mm)的切削参数进行测试分析，如图5、图6所示。通过对所采集加速度信号进行FFT变换，观察其时域信号及频域信号的特征，判断是否发生颤振。

图4 考虑过程阻尼和不考虑过程阻尼的稳定性叶瓣图

图5 A点加速度时域及频域信号(n=400 r/min,a=1.5mm)

图6 B点加速度时域及频域信号(n=400 r/min,a=2mm)

从图4可以看出A点时域信号平稳可靠幅值较小，频域信号所显示的频率主要发生在齿频(400×6/60=40 Hz)及其倍频处。此时，铣削加工过程稳定，没有出现颤振现象。而在观察图5时，可以看出B点的时域信号幅值明显增大，并在频域信号中出现了除齿频及其倍频以外的新的振动频率主要峰值频率为592 Hz、1 184 Hz、1 776 Hz、2 368Hz、2 960 Hz，这些频率均为592 Hz的倍频。根据再生型颤振理论，倍周期分叉频率fPD和准周期分叉频率fH表示两种形式的再生型颤振频率，其计算式分别为

(11)

(12)

4 结论

(1)在传统的铣削动力学模型基础上建立了考虑过程阻尼的铣削动力学方程，得出了稳定性叶瓣图。通过铣削试验验证了模型的正确性。

(2)研究结果表明，在低速区，过程阻尼对铣削稳定性很大影响，稳定性区域显著增加。用考虑过程阻尼的铣削动力学方程得到的稳定性叶瓣图，比用传统的铣削动力学方程得到的稳定性叶瓣图精度更高。为铣削参数的优化提供了理论支撑和依据。