黄山松林分生物量经验收获表研究
华伟平,丘 甜 ,江希钿 ,盖新敏 ,黄烺增
(1.福建省生态产业绿色技术重点实验室,福建 武夷山 354300;2.武夷学院 生态与资源工程学院,福建 武夷山 354300;3.武夷学院 商学院,福建 武夷山 354300;4.福建农林大学 林学院,福建 福州 350002;5.宁德市林业局,福建 宁德 352100)
应用单木生物量表需经过每木调查取得各径阶株数,才能求得林分的产量和产值,该表的优点是既可求得径阶的产量,又能获得整个林分的产量,所得到的信息比较详细,其结果较精确,适合于单个或少数小班的的生物量分析。但在大面积的森林调查中,若对每个小班均进行每木调查,显然工作量太大。因此,有必要建过系列研究方法建立林分生物量模型,并研制林分生物量经验收获表。目前关于编制林分生物量经验收获表的相关研究未见报道。
编制林分生物量表最重要的就是需要建立黄山松林分生物量模型[1],该模型的建模原理与方法基本技术思路为:选择多个模型,对模型自变量加以组合变化来构建生物量估测模型,而估算林分生物量时必须考虑将林分密度引入林分生物量估算模型中,并避免出现总量与分量不兼容的问题,采用二级非线性模型联合估计。
针对现行的大面积森林资源调查特点,建立以林分平均年龄、平均胸径和平均树高为辅助变量建立与黄山松树干(木材、树皮)、树冠(树枝、树叶)、树根有关的林分生物量收获表,用于监测森林生态系统中碳储量的变化规律具有重要的生态环境意义,同时为计划、环境、林业等部门制定节能减排、造林等计划提供参考依据。
1 研究材料
在福建黄山松分布区,选择样地,利用罗盘仪设置临时样地,样地面积0.067 hm2,采用皮尺收集林木空间位置、测高器和围径尺采集林木高度和口径(起测直径为5 cm),并收集林下植被及环境因子等。收集固定样地数据,包括小班实物量表、林业基本图像、伐区设计等材料。历时10 a,收集了253块样地。林分立地质量等级包括4种地类,即肥沃地类、较肥沃地类、中等肥沃地类、瘠薄地类。根据样地每木调查结果,伐倒1~3株不同胸径的黄山松样木,按1 m为区分段,用围径尺测定样木各区分段带皮和去皮口径及梢头底直径、胸径,皮尺测定树高,按树干长度的0、0.25、0.5、0.75处各取5 cm厚的圆盘,并将树枝、树叶、树根等样品带回实验室烘干,获得各部位生物量数据,同时在林业生产相关部门收集采伐数据,共收集291株样木,测量的主要林分因子见表1。

表1 样地及样木情况†Table1 Sample plots and sample plots
2 收获模型的选择与设计
2.1 林分生物量模型的设计
林分生物量模型需考虑林分密度,同时将其它林分因子(平均胸径、平均树高、蓄积量)引入到估测模型中,所以林分生物量估测模型公式[1]为:
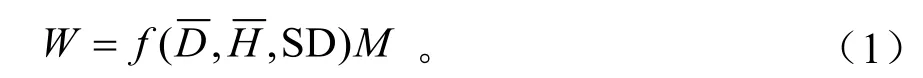
式(1)中:W为林分估测(树干、木材、树皮、树冠、树枝、树叶、树根)生物量;为林分平均胸径;为林分平均树高;M为林分蓄积量。
其中SD为林分相对密度,公式如下:

式(2)中:N为现实林分每公顷株数;Nmax为与现实林分具有相同平均胸径时的每公顷最大株数。
根据通式,本次采用彭小勇[1]构建的林分生物量模型,具体如式(3)~式(6)所示:

结合收集的样地数据,采用SPSS软件求解模型参数,根据相关指数、平均系统误差绝对值、平均相对误差等3个指标选出树干、木材、树皮、树冠、树枝、树叶、树根最优方程,方程拟合效果见表2。
在平均系统误差绝对值小于3%、平均相对误差小于10%的前提下,以相关指数越大、平均系统误差绝对值和平均相对误差越小的选优原则进行筛选。因此,根据表2可知,树干、木材、树皮、树冠、树枝、树叶、树根分为:

式(7)~(13)中:a1i、a2i、a3i、a4i为模型参数,其中i取1,2,3,…。

表2 方程拟合效果Table2 Equation fitting effect
2.2 地位指数曲线模型的设计
利用采集的圆盘数据进行树干解析,获取树干解析数据。将数据进行散点分析,发现理查德模型能较好地描述黄山松优势高随年龄变化的生长规律,即:

式(14)中:Hu为林分优势高;t为林木生长时间;a、b、c为与林分立地质量有关的模型待求参数。
由于不同立地环境条件下,林木生长情况也不同,主要体现在Hu不同,同时,为了紧密结合福建省森林资源清查中有关技术及林业生产实际,按4个立地质量等级,将理查德模型进行设计,参数a、b、c作为肥沃地类(I1)、较肥沃地类(I2)、中等肥沃地类(I4)、瘠薄地类(I4)的函数[2],即a=f1(I1,I3,I3,I4),b=f2(I1,I3,I3,I4),c=f3(I1,I3,I3,I4),其公式为:
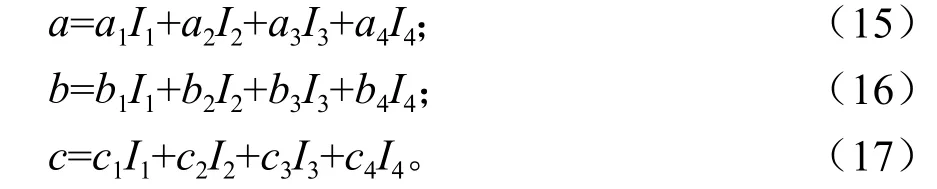
式(15) ~(17) 中:a1、a2、a3、a4、b1、b2、b3、b4、c1、c2、c3、c4为模型参数。
综上所述,本次构建的黄山松地位指数曲线模型为:

式(18)是基于I1、I3、I3、I4为虚拟变量、t为自变量的黄山松地位指数模型。虚拟变量只取0或1,其很好地将I1、I3、I3、I4定性数据转化为定量数据,取值规则为:若立地质量为某个等级时,则该立地质量的等级取值1;其它立地质量等级取值0[3]。
2.3 林分断面积模型的设计
林分断面积是计算或估计蓄积量的重要调查因子,其模型是全林分模型的基本模型之一,目前应用较多的断面积模型为Korf方程[4],其公式为G=Aexp[-K/tC],其中A、K、C为模型参数。A是模型极限值,即林分断面积生长的极限,与立地环境有关;K为常数;C是与密度有关系的曲线形状,本次设计为与林分相对密度有关的关系模型。因此,构建的用于估计黄山松林分断面积的模型为:
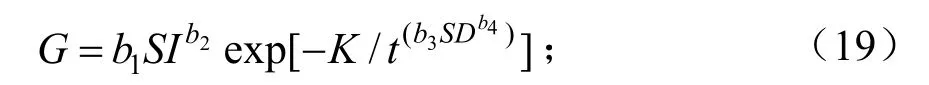
式(19)中:SD为林分相对密度,具体见式(2)。
2.4 林分平均胸径和株数模型
根据前人的研究[4],林分胸径、株数与林分断面积、相对密度间的关系如下。

式(20)和式(21)中:α、β为模型参数。利用样地数据,经SPSS软件计算,得到α=34 674.2、β=1.248 8。
3 研究结果
3.1 基于联合估计法的生物量模型
根据林分生长量模型的筛选过程,设计、确定了不同部位的林分生长估计模型,但这些模型都是相互独立,若采用独立建模,必然出现总生物量与对应的各部位生物量合计值不相等的逻辑问题。因此为避免不兼容的问题,本次使用二级非线性模型联合估计[1],使林分木材生物量加林分树皮生物量等于林分树干生物量,林分树冠生物量等于林分树枝生物量加树叶生物量,林分树干生物量与林分树根生物量相加等于林分总生物量。
在建模过程中,为提高建模样本数量,采用交叉建模和检验技术,其技术思路为:将参加建模的所有样本数据按从小到大排序,然后按1、2、3进行重复编号,直到所有样本均标记编号,编号相同的为同组,共计3组;交叉建模及检验过程共3次,2组作为建模样本,另1组为检验样本进行F检验;3次建模F检验经通过后,将所有样本用于生物量模型拟合[5-6]。
在建模过程中,为提高拟合精度和收敛速度,采用混合蛙跳算法(SFLA)求解方程参数。该算法是一种后启发式的智能算法,应用时间不长(Eusuff等提出,2003),但其不仅继承了其他算法的优点,而且具有收敛速度更快,最优的求解能力更强,具体算法流程见图1[7-8]。
根据交叉建模和交叉检验同步进行的计算思路,经计算,3次建模均通过F检验,其值分别为2.33、2.94、2.17。将所有样本进行建模,经SFLA迭代求解模型参数,建立的林分各分量及总量生物量见式(22)~(29),并利用平均系统误差(ASE)、平均相对误差绝对值(AARE)等指标进行评价[6],其ASE(2.381%)、AARE(7.964%)均在±10%内。
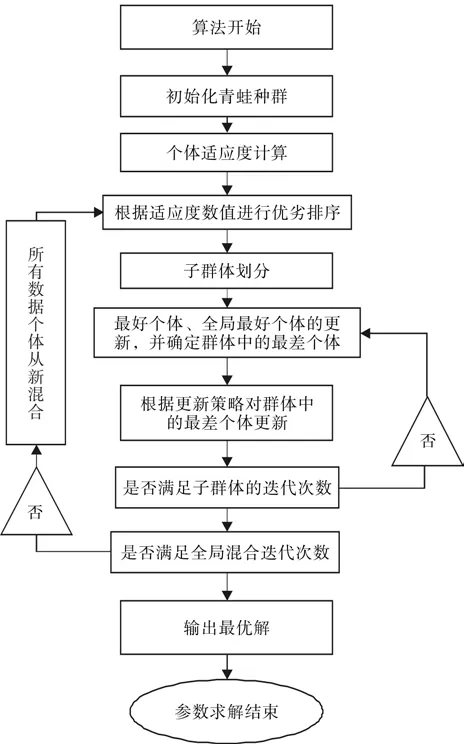
图1 基于混合蛙跳算法的参数求解流程Fig.1 Parameter solution process based on shuffled frog leaping algorithm



3.2 全林分模型
为了便于应用林分生物量,采用经验收获表作为研制黄山松生物量收获表的依据。
1)地位指数曲线模型的建立
式(18)无法用最小二乘法求解,SFLA来估计模型参数。利用肥沃地类、较肥沃地类、中等肥沃地类、瘠薄地类的样地材料,经SFLA迭代求解模型参数,求得各参数及拟合情况见表3。

表3 模型拟合参数Table3 Model fitting parameters
相关指数0.987,说明拟合效果较好。将21个未参加建模样本材料进行适用性检验[6],其ASE 1.986%、AARE 6.878%,即2个指标均在±10%内,预测精度较高、适用,可用于黄山松林分生物量经营收获表的编制。
由于Hu能很好地反应立地质量或立地条件,但在过去林业生产实践上,一般缺少Hu数据,造成地位指数判断困难,而是林分调查的基本因子之一,以往我国森林调查体系均有[9]。因此,本研究通过建立与Hu的关系模型,解决Hu的估算问题,同时在缺乏数据的情况下,可用关系模型推算。根据前人的研究[9-10],他们之间呈直线关系,具体见式(30)。

式(30)也可写成下式:

由于式(30)、式(31)描述的是同一个函数关系,故必须有:

但在采用最小二乘法配置的回归直线式(30)、式 (31)不是同一个直线,即a、b与a′、b′不满足式(32)、式(33)的关系。为解决这一问题,可以采用对偶回归分析法,结果如下:

2)林分断面积模型
式(19)同样采用SFLA迭代求解模型参数。经计算机迭代计算,求得式(19)中的5个参数及相关指数为:b1=12.947 8,b2=0.576 4,K=4.237 1,b3=0.594 8,b4=0.578 41,R2=0.964。
3)林分蓄积量模型
林分蓄积量是森林调查最重要因子,也是森林生长和收获预估的重要对象[4]。因此,本次在编制生物量经验收获表时,同样将林分蓄积量作为其中一列项目,而建立林分蓄积量模型就显得至关重要。现以t、SI、G为自变量,并进行变换和组合,使用逐步回归技术建立林分蓄积量模型。
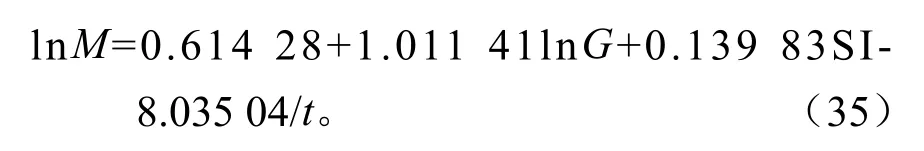
4)林分相对密度模型
林分生物量模型、林分断面积模型分别描述了不同立地上各种密度水平的林分生物量、林分断面积生长过程,而经验收获表反映的是编表地区具有平均密度的林分调查因子的生长情况。因此,需对林分生物量模型、林分断面积模型中的林分相对密度在不同条件下取一定值。由于优势高是年龄和立地的函数,优势高的大小是年龄和立地的综合体现。因此可将林分相对密度作为优势高的函数。利用样地材料,建立的林分相对密度模型为:

3.3 生物量经验收获表的编制
依据研究所建立的林分平均胸径、平均树高、断面积模型、形高模型、蓄积量模型,给定地位指数为14、立地质量等级为肥沃,即可得到优势高、林分蓄积量随林分年龄的变化量,并确定林分相对密度、林分平均高,经式(19)~(21)计算得到林分断面积、平均直径、株数。将林分蓄积量与林分相对密度、林分平均胸径、平均树高带入林分生物量估测模型中即可得到林分树干、林分树冠、林分木材、林分树皮、林分树枝、林分树叶、林分树根、林分总生物量,最后按各部位展开即可得获到林分生物量经验收获表,具体结果见表4。
4 结论与讨论
鉴于目前大量研究中生物量模型一般未引入林分密度或间接将蓄积量作为其中的一个变量的情况,本研究将林分相对密度指数与蓄积量同时引入到模型中,并建立了兼容性黄山松生物量模型,结合地位指数模型、林分断面积、林分蓄积量、平均胸径和株数等全林分模型,编制了黄山松生物量经验收获表,为不同立地质量等级、林分密度的黄山松经营管理提供技术指导,在监测森林生态系统中碳储量的变化规律方面具有重要的生态环境意义。
研究发现黄山松林分生物量与平均胸径、平均树高、相对密度指数、蓄积量等林分因子之间关系较高,确定了描述树干、木材、树枝、树叶、树根与林分因子之间关系的最佳模型为描述树冠与与林分因子之间关系的最佳模型为为黄山松生物量、碳汇估算提供技术支持。为避免各部位生物量之和与总量不符的逻辑问题,提高样本拟合数量,采用二级非线性模型联合估计来解决总量与分量模型不兼容的问题,通过交叉建模和检验技术提高建模样本数量,为其他林分模型的建模提供技术参考。

表4 林分生物量经验收获Table4 Forest biomass experience yield
在全林分建模过程中,与同行研究比较[11-13],本次研究先建立可变密度的林分收获模型,再根据优势高与林分相对密度的关系确定林分平均收获量,不仅可用于编制林分经验收获表编制,而且为黄山松林分可变密度收获表的编制提供林分模型。经混合蛙跳算法求解,得到的林分模型拟合效果较好。在建模过程中,与其他智能算法比较,虽然混合蛙跳算法具有具有收敛速度更快、最优的求解能力更强,但未与其他智能算法作研究比较,无法比较其他算法的在本研究模型参数求解的优劣,这将在今后研究中作进一步分析。

