连续波核磁共振实验问题探究
李潮
(中山大学 a.物理国家级实验教学示范中心;b.物理学院,广东 广州 510275)
连续波核磁共振是近代物理实验课程的重要教学内容,也是实验课堂讨论的热点项目. 教学装置的实验模块功能清晰,实验物理图像多姿多彩,这为实验课堂提供了丰富的讨论素材. 然而,由于测量技术方法不够直观,同时学生普遍对核磁共振实验原理和实验电子技术原理缺乏深刻理解,增加了实验课堂讨论难度. 对于绝大多数实验测量,施加激励与拾取响应分别由不同功能单元实施. 然而,在连续波核磁共振[1-3]测量中,LC谐振单元不仅独立承担了这2种功能,而且无需“角色”切换即可“一气呵成”地完成从施加激励到拾取响应的实验全程. 如果认为实验原理即是实验物理原理和实验技术原理,那么掌握LC谐振频率特性[4-5]及检波(解调)技术是正确理解和分析核磁共振实验数据的重要基础. 在使用边限振荡器[6]的连续波核磁共振实验中,衰减的共振尾波振荡频率并非(且远小于)外磁场中处于激发态核磁矩拉莫频率,而且它明显受到调制磁场强度及其增速的影响. 准确拾取被测对象对激励(作用)的响应信息是核磁共振实验的关键环节. 只有深入了解连续波核磁共振信号拾取方法,才能深刻理解共振尾波的物理涵义,从而掌握核磁共振实验原理. 本文以LC谐振频率特性为切入点,根据简单的数理分析结果设计物理实验,通过实验事实探究连续波核磁共振信号的拾取方法和共振尾波的物理性质,进而深入分析调制磁场和弛豫时间对共振尾波的影响以及实验现象的物理本质.
1 实验技术方法
连续波核磁共振实验装置主要包括稳恒外磁场、产生偏振射频电磁波(光子)的(边限)振荡器和低频调制磁场等3部分. 振荡器(检波输出)提供了共振信号拾取功能,同时借助低频调制磁场寻找且获得周期性共振吸收信号,便于(示波器)实验观测. 不管是调节变容二极管反向偏置电压改变振荡器LC谐振频率的扫频法,还是调节直流励磁电流改变稳恒外磁场强度的扫场法,一旦满足能量守恒和角动量守恒,即可发生核磁共振吸收. 共振激发是瞬时完成,且相干. 随着调制磁场穿越并偏离共振点,处于激发态粒子也随之逐渐回到基态. 显然,激发态寿命决定了粒子回到基态所需时间(或称之为弛豫). 共振尾波就是核磁共振弛豫[7-9]的宏观表现. 事实上,核磁共振尾波记录了激发之后,处于激发态核磁矩拉莫进动在射频线圈中所产生的感生电动势变化. 由于稳恒外磁场强度不变,处于激发态核磁矩拉莫频率将随调制磁场强度改变,相应的感生电动势也随拉莫进动同频变化.
正确理解连续波核磁共振尾波物理涵义的关键是准确分析LC谐振回路在共振激发及随后的信号拾取中的作用,并充分认识共振弛豫对后续激发—拾取的影响. 由上述分析可知,完成核磁共振激发后,LC回路信号包含着自身的谐振信号A(ω0)sin (ω0t+α)和在外磁场中处于激发态核磁矩拉莫进动感生电动势B(ω)sin (ωt+β)两部分的贡献. 因此,LC谐振回路(单元)所拾取信号(电压)可表示为
S(t)=A(ω0)sin (ω0t+α)+B(ω)sin (ωt+β),
(1)
其中,A(ω0)和B(ω)分别为谐振信号幅值和感生电动势幅值,ω0和ω分别为LC谐振角频率和核磁矩拉莫(角)频率,α和β分别为上述2种信号的初相位.
令ω=ω0+Δω,β=α+φ,式(1)可改写为
S(t)=A(ω0)sin (ω0t+α)+
B(ω)cos (Δωt+φ)sin (ω0t+α)+
B(ω)sin (Δωt+φ)cos (ω0t+α)=
[A(ω0)+B(ω)cos (Δωt+φ)]sin (ω0t+α)+
B(ω)sin (Δωt+φ)cos (ω0t+α)=
R(ω,ω0)sin (ω0t+α+θ),
(2)
其中,
且令
(3)
利用a2+b2≥2|a·b|,且|cos (Δωt+φ)|≤1,取式(3)一级近似可得
(4)
令
(5)
(6)
则式(1)可表示为
S(t)=[C+Dcos (Δωt+φ)]sin (ω0t+α+θ).
(7)
上述近似方法所得结果表明,LC谐振单元所拾取的信号是以频率ω0的LC谐振信号为载波,其幅值受频率为Δω=ω-ω0(近似于)简谐调制的调幅信号. 采用检波技术,即可测得式(7)中调制信号Dcos (Δωt+φ);进而,由式(6)可获得在磁场中处于激发态核磁矩拉莫进动在射频线圈中的感生电动势B(ω)sin (ωt+β).
主体设备是复旦天欣FD-CWNMR-B连续波核磁共振实验装置,除了完成常规的核磁共振尾波观测,还增加测量2CC13E二极管PN结电容和谐振频率随反向偏压变化,根据上述理论分析方案搭建共振信号拾取方法分析实验. 实验样品1是弛豫时间T1=7.76 ms和T2=6.72 ms的合适浓度CuSO4水溶液,实验样品2是弛豫时间T1=3 299.09 ms和T2=2 578.52 ms的饮用纯净水. 上述弛豫时间均由纽迈NMI20-015V-I核磁共振成像分析仪测量. 使用Tektronix FCA3000频率计和TBS2104数字示波器分别测量振荡器工作频率及其(检波)输出信号. 中大科仪OE1022D双通道锁相放大器用于测量2CC13E二极管PN结电容[10],且由普源DP831A直流电源提供反向偏置电压. 使用Tektronix AFG3252信号源为Lp=2.53 μH外部线圈提供频率可调的射频驱动,且由该线圈发射射频信号. 通过耦合至边限振荡器的样品线圈(2个线圈正对但不接触,距离约1.5 cm),模拟外磁场中核磁矩拉莫进动在射频线圈中所产生的感生电动势. 为配合远程(跨校区)物理实验示教[11],上述实验都使用计算机通过GPIB,RS232和USB接口实施测控及数据采集分析.
2 实验问题探究
2.1 LC谐振频率及调节
核磁共振测量的关键功能单元是LC谐振电路,其幅频和相频特性是边限振荡器的技术原理基础. 采用锁相放大技术[5]和数字示波器[12](结合离散傅里叶变换)测量分析LC频率特性,不仅是了解谐振频率测定方法,更是深刻理解核磁共振测量分析的基础实验. 在连续波核磁共振实验中,利用变容二极管PN结电容随反向偏压变化特性,通过改变反向偏压调节LC谐振频率. 振荡器所用2CC13E结电容及由它组成的LC回路谐振频率随反向偏压变化情况如图1所示.
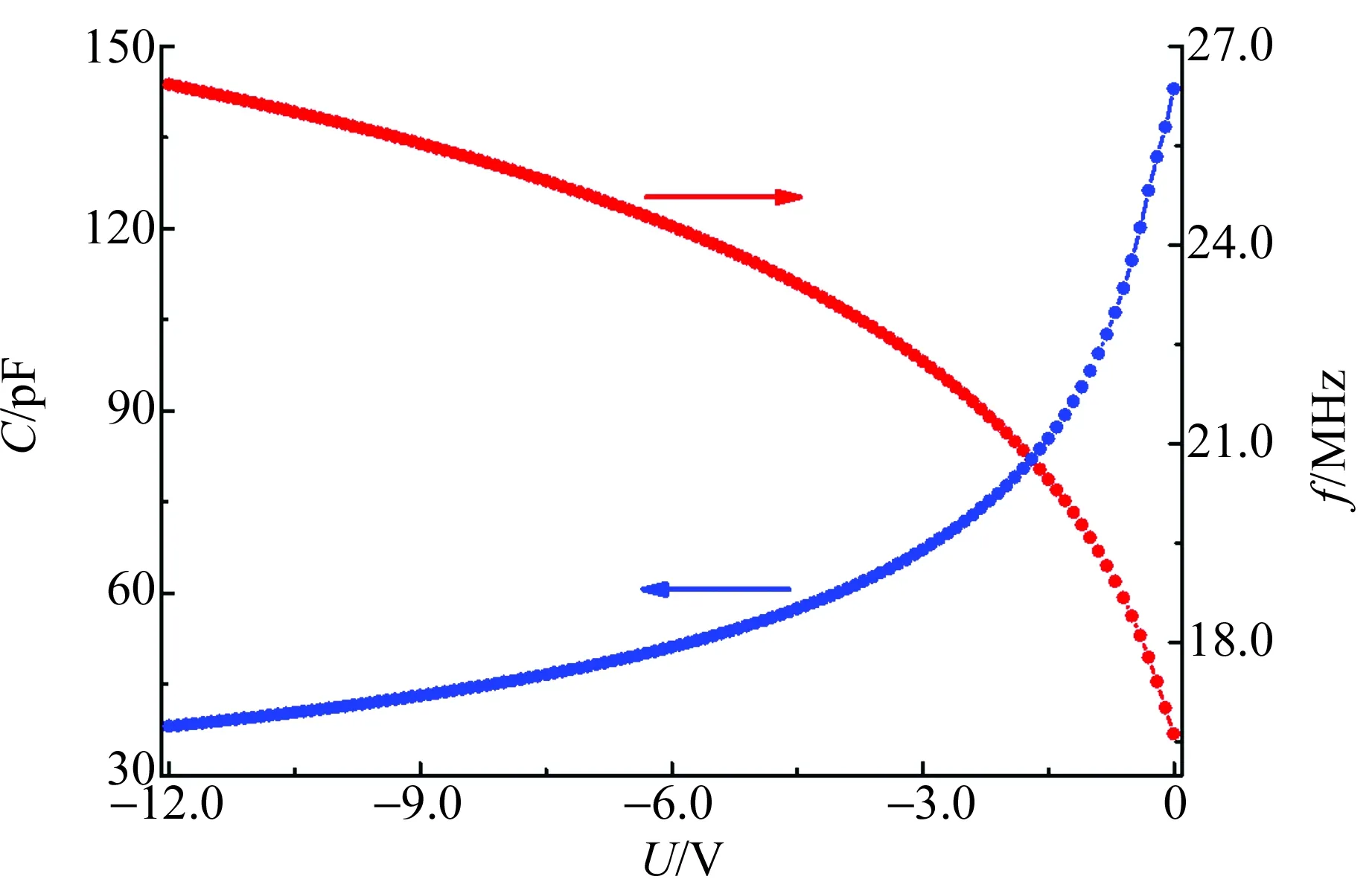
图1 结电容和谐振频率随偏压变化
由图1可见,当偏压小于3.0 V时,曲线比较陡峭,表明结电容随偏压变化敏感;在偏压较高区域,曲线比较平缓,说明结电容随偏压变化相对迟缓.LC谐振频率由结电容和射频线圈电感共同确定,实验结果表明,处于低偏压区时偏压改变(或漂移)可引起谐振频率明显变化;若工作于高偏压区,则可提高LC回路谐振稳定性.
2.2 共振信号拾取
通过频率可调的外部射频信号耦合模拟外磁场中核磁矩拉莫进动感生电动势. TBS2104数字示波器所记录的振荡器(检波)输出如图2所示,输出近似于简谐信号说明上述分析方法合理. 尽管在上述数理分析中使用角频率描述物理参量,而实验测量中则以频率表示,但为便于论述,以下对角频率和频率不作区分说明. 比较FCA3000频率测量值和AFG3252输出信号频率可知,TBS2104测量的谐振信号频率近似等于外部射频信号频率与振荡器工作频率之差(绝对值). 由此说明,由振荡器(检波)输出可以获得式(7)的调制信号Dcos (Δωt+φ).
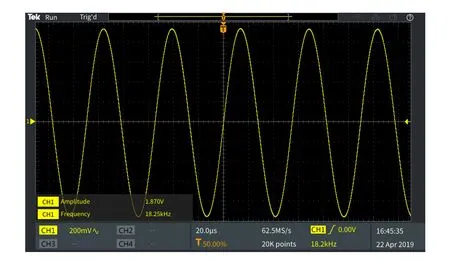
图2 边限振荡器输出信号截图
图3更准确地显示了外部信号频率ω、振荡器工作频率ω0及其(检波)输出信号(调制)频率ω1三者之间关系,其中Δω为FCA3000频率测量值ω0与AFG3252输出信号频率ω之差,ω1为由TBS2104测得的调制信号Dcos (Δωt+φ)的频率. 图3显示,调制频率ω1与差频Δω=ω-ω0线性相关,且在实验范围内符合|ω1|=|ω-ω0|.
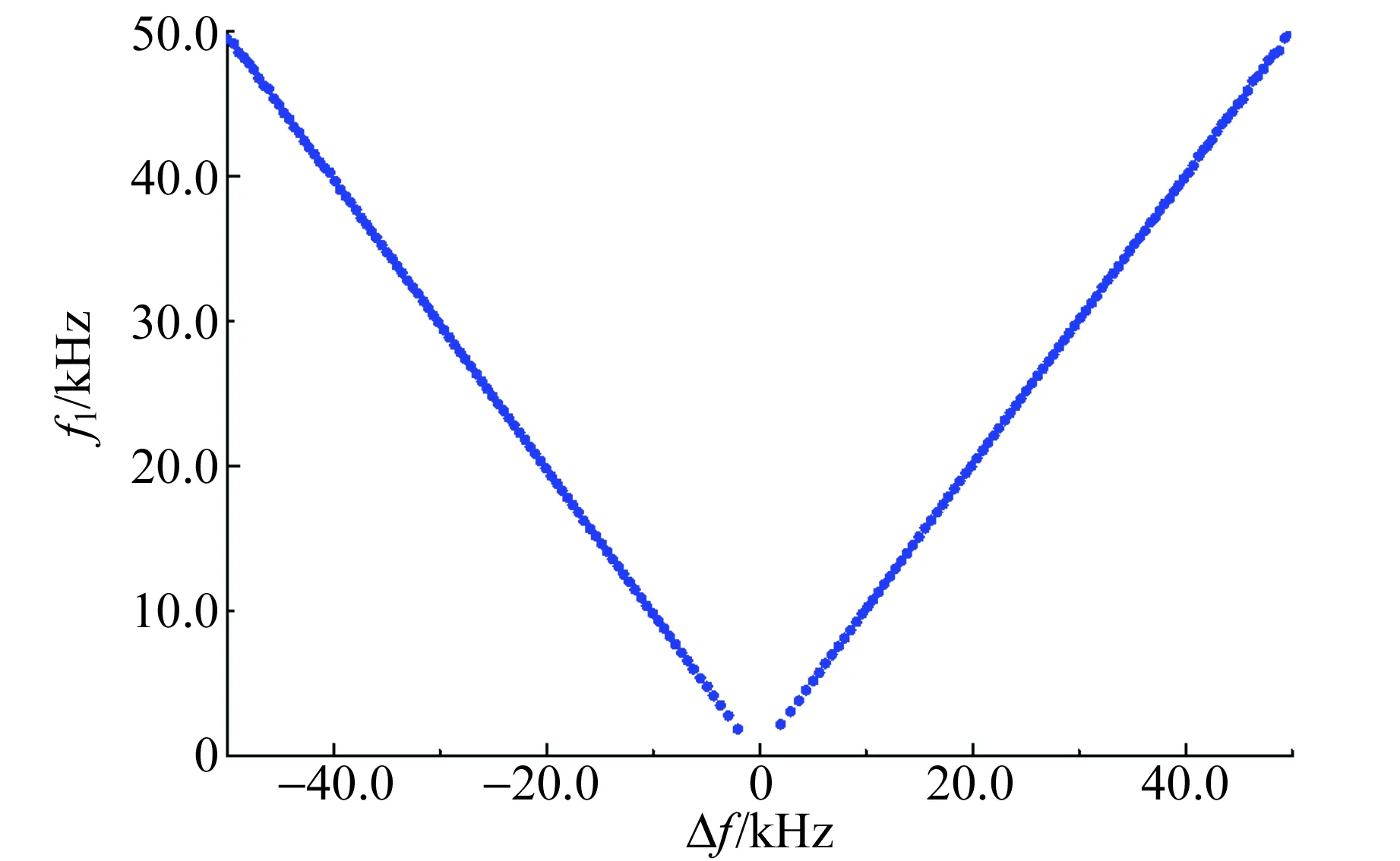
图3 调制频率与拉莫频率和谐振频率差频的关系
在实验测量的频率范围内,维持外部信号(感生电动势)B(ω)sin (ωt+β)的幅值B(ω)基本恒定. 图4实验结果显示,振荡器(检波)输出的调制信号Dcos (Δωt+φ)幅值随差频(绝对值)Δω=|ω-ω0|明显改变. 图4中调制信号幅值由TBS2104测量,而且采用峰-峰值表示,Δω,ω0和ω与图3的测量方法以及数据处理方法相同.
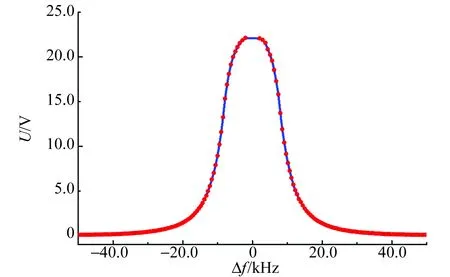
图4 振荡器(检波)输出信号频率特性
由图4可见,当外部信号频率ω处于LC回路谐振频率ω0附近时,振荡器(检波)输出的调制信号幅值(或称为调制深度)达到最大, 随频率偏离ω0而逐渐减小. 由于实验中保持B(ω)基本恒定,调制信号幅值变化由LC谐振回路的频率特性决定. 这一实验事实也表明,当外部信号频率ω较大偏离LC回路谐振频率ω0时,测量所得的调制信号幅值已不能真实描述外部信号的物理参量. 以本实验所使用的边限振荡器为例,其调制信号半高的频宽约20.00 kHz. 因此,只有共振尾波振荡频率(即上述的调制频率)处于半高频宽之内,才能保证射频线圈中感生电动势合理描述共振尾波幅值. 事实上,这也是调幅收音机的选台原理.
2.3 共振尾波分析
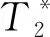
当每个调制磁场周期出现2次等间隔共振信号时,表明核磁共振正发生在稳恒磁场强度处,此时样品1的共振波形如图5所示.
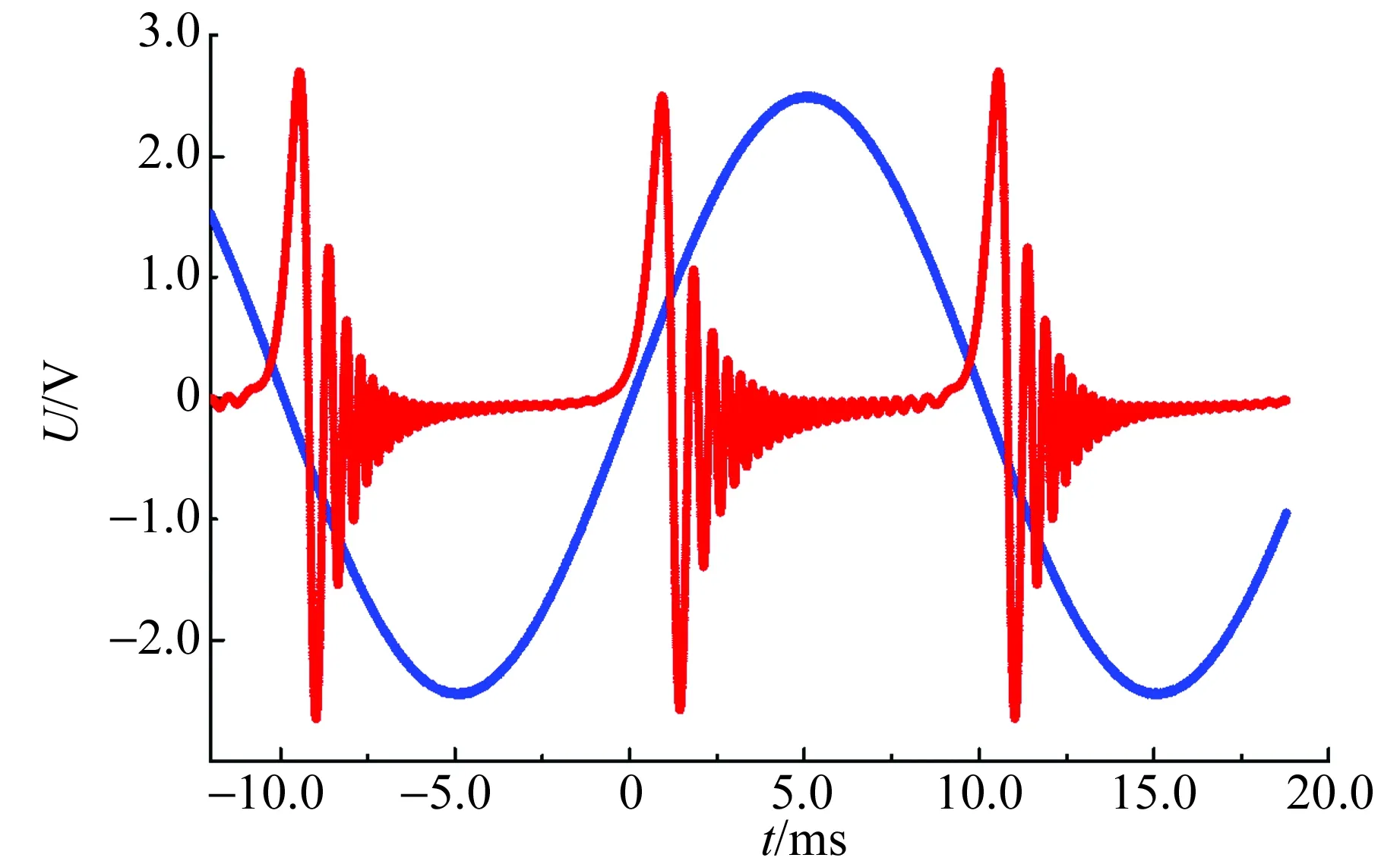
图5 短弛豫弱调制磁场连续波核磁共振波形
调整样品射频线圈推杆方位,消除调制磁场在线圈引线闭会回路的磁通量变化,使处于调制磁场前半周和后半周共振尾波基本相同[7]. 当使用频率为50 Hz调制磁场,即共振激发重复时间为10 ms时,可认为在每次产生激发之前,弛豫时间T1=7.76 ms和T2=6.72 ms的样品1粒子已全部回到基态,从而消除共振激发历史的影响. 图6更清晰地显示了图5中单个共振尾波情况.
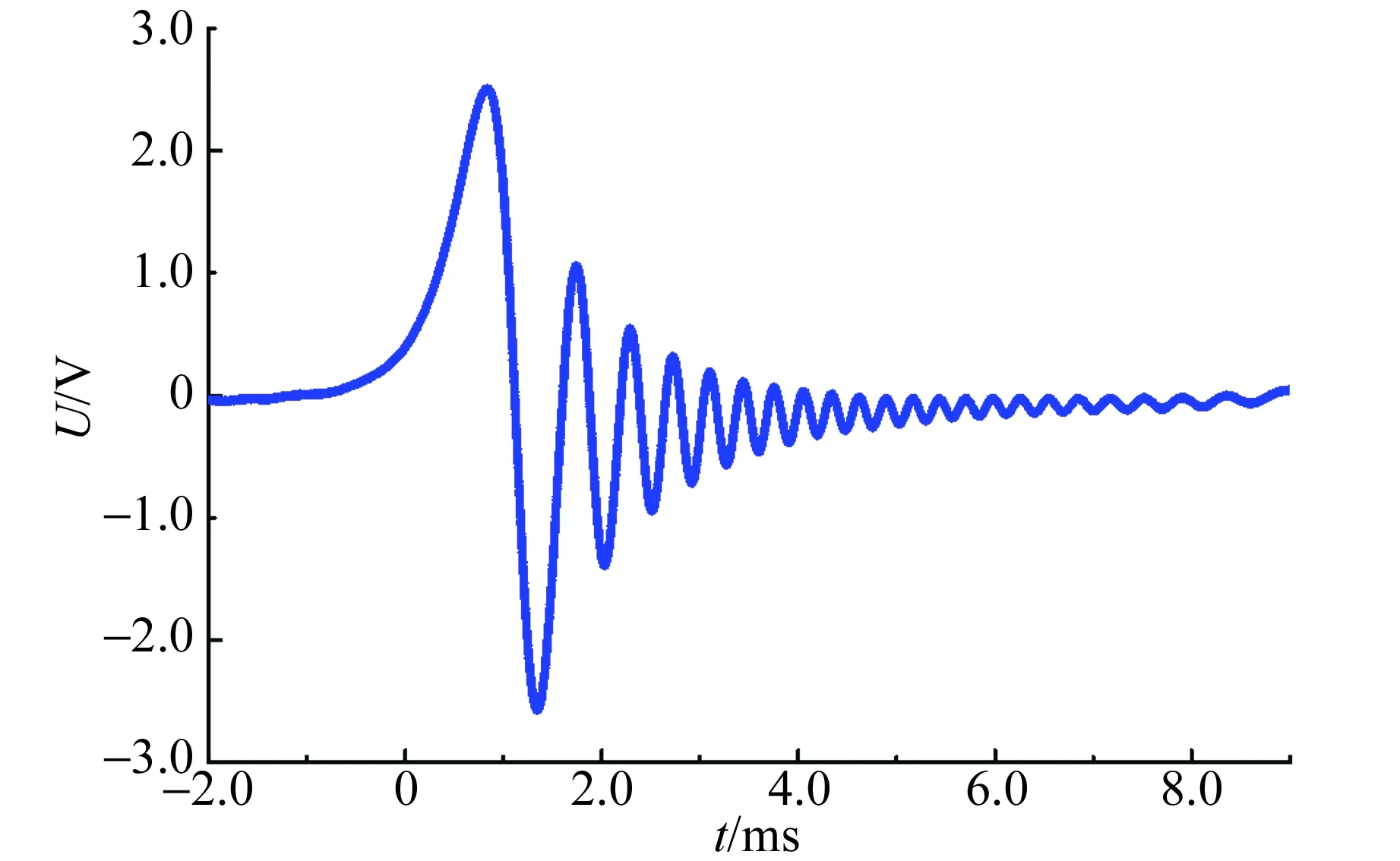
图6 短弛豫弱调制磁场核磁共振尾波
上述分析结果表明,在连续波核磁共振实验中,边限振荡器(检波)输出信号幅值反映了处于激发态核磁矩拉莫进动感生电动势,它代表了此时激发态核磁矩数量,而其振荡频率则为拉莫频率ω与LC谐振频率ω0之差Δω. 随着激发完成,调制磁场穿越共振点,处于激发态核磁矩拉莫频率ω也随之偏离了共振频率(即LC谐振频率)ω0. 频率偏离量Δω正比于作用在样品的调制磁场强度,显然它就是LC回路调幅信号的调制频率,也正是振荡器(检波)输出共振尾波的振荡频率. 调制磁场偏离共振点越远处,共振尾波频率也随之越高. 由图6可以看出,随着调制磁场穿越并且逐步远离共振点,核磁共振尾波频率随之逐渐增加.
微调LC谐振频率使核磁共振吸收发生在调制磁场峰或谷附近. 图7显示了处于调制磁场峰附近的共振波形.
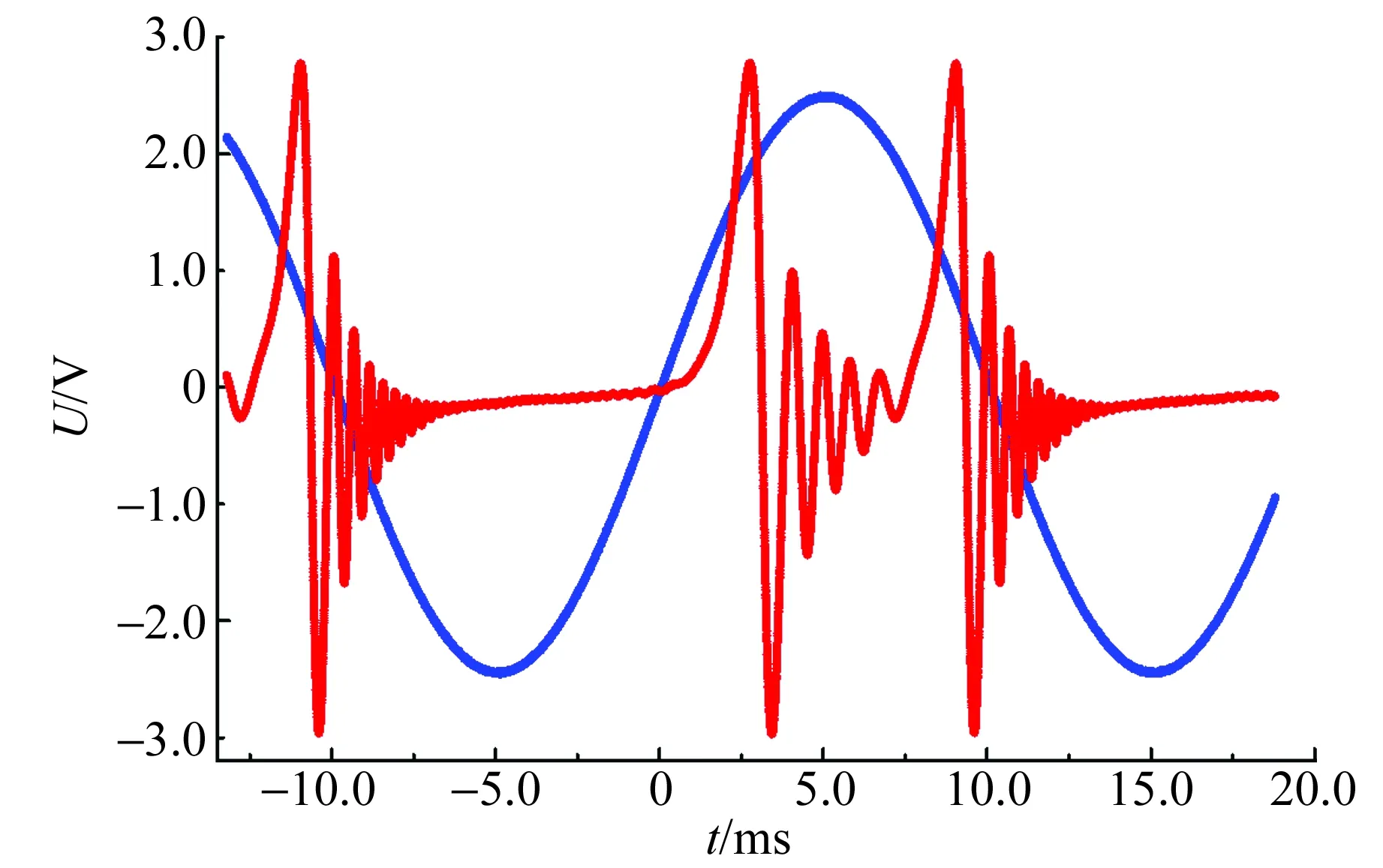
图7 短弛豫弱调制磁场近峰处核磁共振波形
当核磁共振发生在(靠近)调制磁场峰前时,由于随后调制磁场强度增速较小(平缓),激发态核磁矩拉莫频率相对LC谐振频率(即共振频率)变化不大,从而共振尾波频率较低. 对于核磁共振发生在(背离)调制磁场峰之后情形,由于随后调制磁场强度增速较大(陡峭),激发态核磁矩拉莫频率变化明显,因此共振尾波频率也较高. 图7实验结果再次验证了共振尾波频率随调制磁场强度变化,而且调制磁场强度增速影响激发态核磁矩拉莫频率的变化率. 或者说,连续波核磁共振尾波频率由偏离共振的调制磁场强度所决定,而且共振尾波频率变化率反映了调制磁场强度增速.
2.4 长弛豫现象
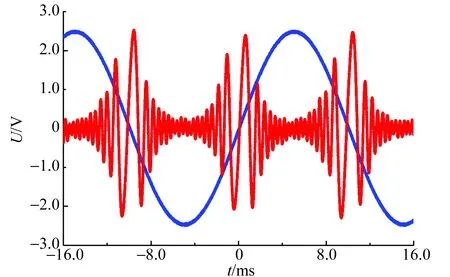
图8 长弛豫弱调制磁场连续波核磁共振波形
对于长弛豫情形,由于横向弛豫时间比激发重复时间长,每次共振激发之前激发态仍然有部分尚未回到基态的受激核磁矩. 如上所述,这些受激核磁矩在外磁场中拉莫进动也必将在射频线圈中产生同频的感生电动势. 随着调制磁场靠近共振位置,一旦拉莫频率进入LC谐振频率特性峰范围,其感生电动势可以被拾取. 由图4振荡器(检波)输出信号频率特性可以看出,随着拉莫频率与LC谐振频率(即共振频率)的频差(即幅度调制频率)减小,输出信号幅值逐渐增大. 这就是左侧信号随靠近共振位置,其幅值逐步上升的原因.
针对样品2情形,由于其横向弛豫时间比激发重复时间长3个数量级,可以认为在每个调制磁场周期内,激发态的受激核磁矩数量近似不变. 不管左侧信号还是右侧信号,幅值变化基本由图4频率特性所决定. 因此,当调制磁场周期发生2次等间隔共振激发时,两侧信号是关于共振磁场对称. 总而言之,此时右侧“共振尾波”信号幅值衰减已经不能反映共振弛豫物理过程了.
从实验测量角度,样品共振弛豫长或短是相对共振激发重复时间而言. 当使用100 Hz调制磁场(激发重复时间5 ms)时,弛豫时间T1=7.76 ms和T2=6.72 ms的样品1也可观测到微小左侧信号.
2.5 调制磁场影响
适当增大调制磁场幅值,可观测到如图9所示的样品1实验结果. 由图9可见,共振尾波频率随调制磁场变化规律与图6实验结果一致,但在激发之后相同时刻的共振尾波频率比图6情形的频率略高. 2种情形的差别在于调制磁场强度增速不同,后者比前者更快. 激发是瞬时完成且相干,调制磁场穿越速度并不影响共振吸收,但(随后)调制磁场强度增速却改变了激发态核磁矩拉莫频率的变化率. 因此,在激发之后的相同时刻,后者的共振尾波频率比前者高.
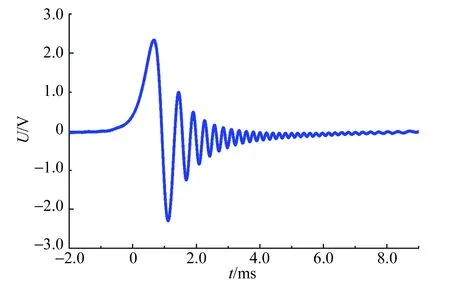
图9 短弛豫适中调制磁场核磁共振尾波
微调LC谐振频率使共振吸收返回稳恒磁场强度处. 随后,在继续缓慢增大调制磁场幅值的调节过程中,除了再次印证图5~7和图9实验结论外,还可观察到图10所示的共振尾波加速衰减现象. 比较图5和图10,可更清晰地看出上述实验事实.
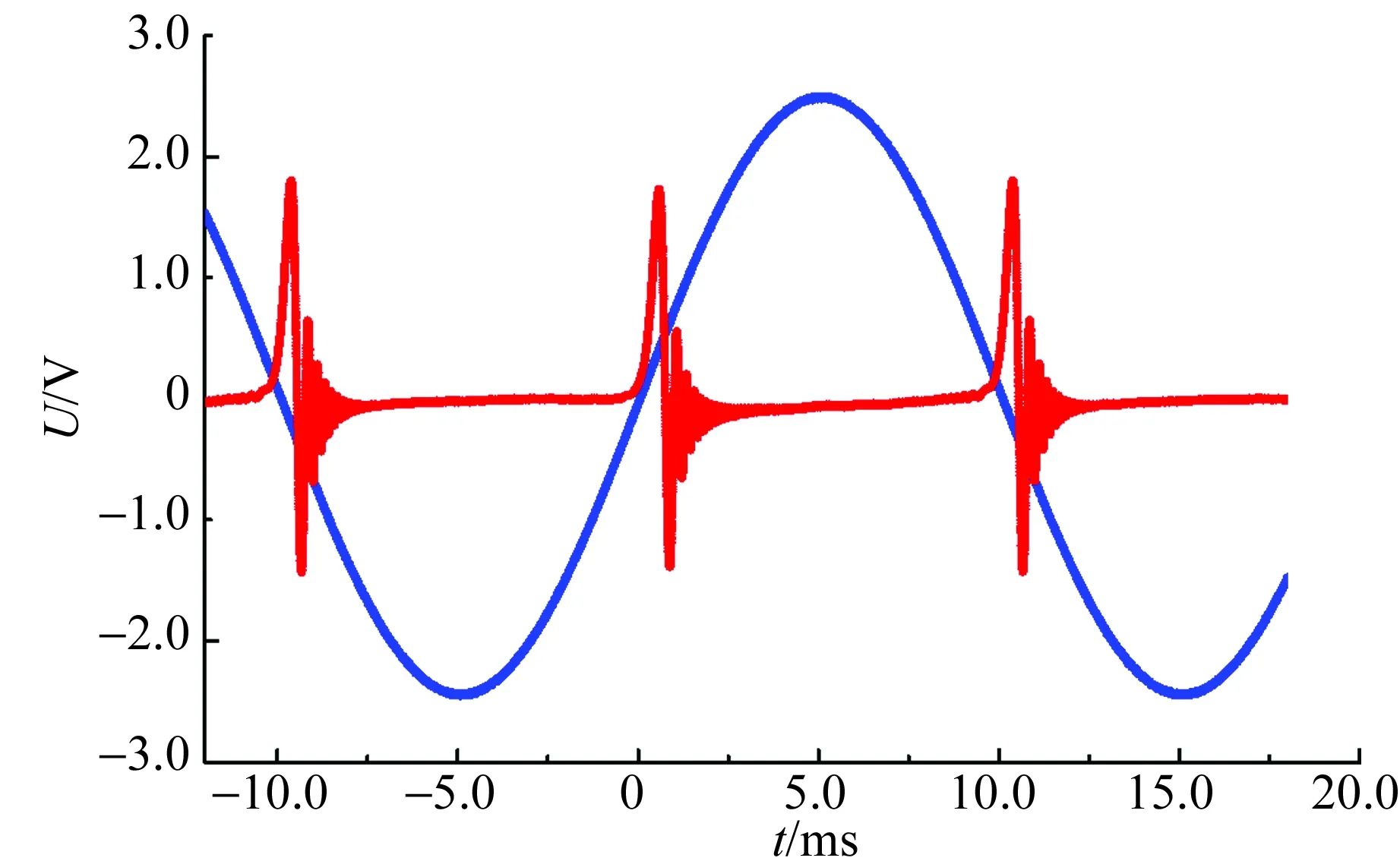
图10 短弛豫强调制磁场连续波核磁共振波形
考虑LC谐振回路的频率特性,只有当拉莫频率处于谐振频率ω0附近时,振荡器(检波)输出的调制信号才可“无损”记录共振尾波. 当调制磁场幅值增速使拉莫频率与共振频率之差超出图4所示的输出信号频率特性峰范围时,(检波)输出的(调制)信号幅值已不能真实描述共振尾波. 进而,图8结果还表明,当调制磁场周期(共振激发重复时间)比样品共振弛豫时间短得多时,不仅出现左侧信号,右侧共振尾波信号也不能真正反映共振弛豫的物理事实.
3 结 论
致谢:感谢北京大学吴思诚教授的教学指导,本文实验设计思路源于吴先生对核磁共振实验原理透彻讲解的启发.

