倾倒非黏性颗粒时漏斗对休止角的影响

施宇轩, 郝成红,黄耀清,尹亮亮

(上海应用技术大学 理学院,上海 201418)

颗粒物质是一类特殊的物质,表现出与固、液、气不同的性质. 许多自然灾害(如泥石流、雪崩、山崩、地震等)都与颗粒物质的崩塌有紧密联系. 因此,颗粒物质崩塌现象的研究就显得十分重要. 已有的关于颗粒物质崩塌现象的研究[1],认为颗粒物质在崩塌过程中存在2个特征角:刚发生崩塌时的特征角被称为崩塌角,崩塌停止时的特征角被称为休止角(又称静止角、安息角). 文献[2-4]研究了颗粒群的质量或颗粒群堆积高度对休止角的影响,本文研究了倾倒使用的漏嘴对休止角的影响.

1 物理模型的建立

1.1 动力学模型

假设已经形成如图1所示的堆积结构[5],图中a为崩塌层,b为锥形结构上原有的1层颗粒群. 颗粒群a下落到图中位置时的速度为v1,此时颗粒群b静止.

分别对颗粒群a和b作受力分析,如图2所示. 图2中m1g和m2g分别为颗粒群a和b的重力,f1和f2分别为颗粒群a和b所受的摩擦力,N1和N2分别为坡面对颗粒群a和b的支持力,F1和F2分为颗粒群a和b之间的相互作用力.

图2 受力分析

设颗粒群b下滑h高度后到达坡面低端,由动能定理可得:

(1)

式中μ为动摩擦因数,h为颗粒群b最低端所在高度,θ为颗粒群b所在母线与平面的夹角. 从式(1)以及图1可以看出,当图示中颗粒群a从漏嘴下落到锥形堆积结构的坡面后,会发生2种情况:

1)速度不够大时,颗粒群a对颗粒群b的作用力F2不足以克服摩擦力f2,而后颗粒堆积直到F2克服f2,颗粒群a和b会下滑至底部；

2)速度足够大时,颗粒群a和b会一起下滑(也就是发生了崩塌),一直沿斜面下滑到底部.

以上2种情况的共同点为最终结果是颗粒下滑到底部,而同时因为颗粒群a上面还会有颗粒继续落下,并会沿斜面堆积起来,达到自组织临界态,继续堆积便会崩塌到外面1层,再循环之前所描述的过程.

从式(1)中,能找到以θ为因变量的函数. 将式(1)化简可得

(2)

式(2)中m1+m2与总质量正相关,h与堆积高度正相关,v1与漏嘴的高度正相关,可以对此做实验验证.

1.2 流体力学模型

大量实验可以得出结论:锥形堆积结构的休止角在各个母线上是不同的，可以使用流体力学的物理模型解释.

因为流动的颗粒群符合流体的定义,所以可将从漏嘴流出的颗粒群理想化为流体来分析. 颗粒群从横截面积为A的漏斗流出,假设其流量为Q,则其流速为

(3)

根据伯努利方程

(4)

式中p是颗粒群所受到的压强,ρ是颗粒群密度. 将式(3)代入式(4)可以得出

(5)

式(5)即是流体压强与管道横截面积的关系.

2 实验探究

使用控制变量法对式(2)和式(5)进行实验探究. 针对下落的高度(即漏嘴与平面的垂直距离)与漏嘴的口径[6]进行实验.

2.1 实验装置

如图3所示,铁架台可减少颗粒群倾倒时整个装置的晃动,使用平口漏斗作为倾倒颗粒的槽道. 该装置优点在于可改变漏斗与高度. 实验中,使用垂直倾倒的方式，倾倒结束后利用投影法分别测量投影图案的左右角度.

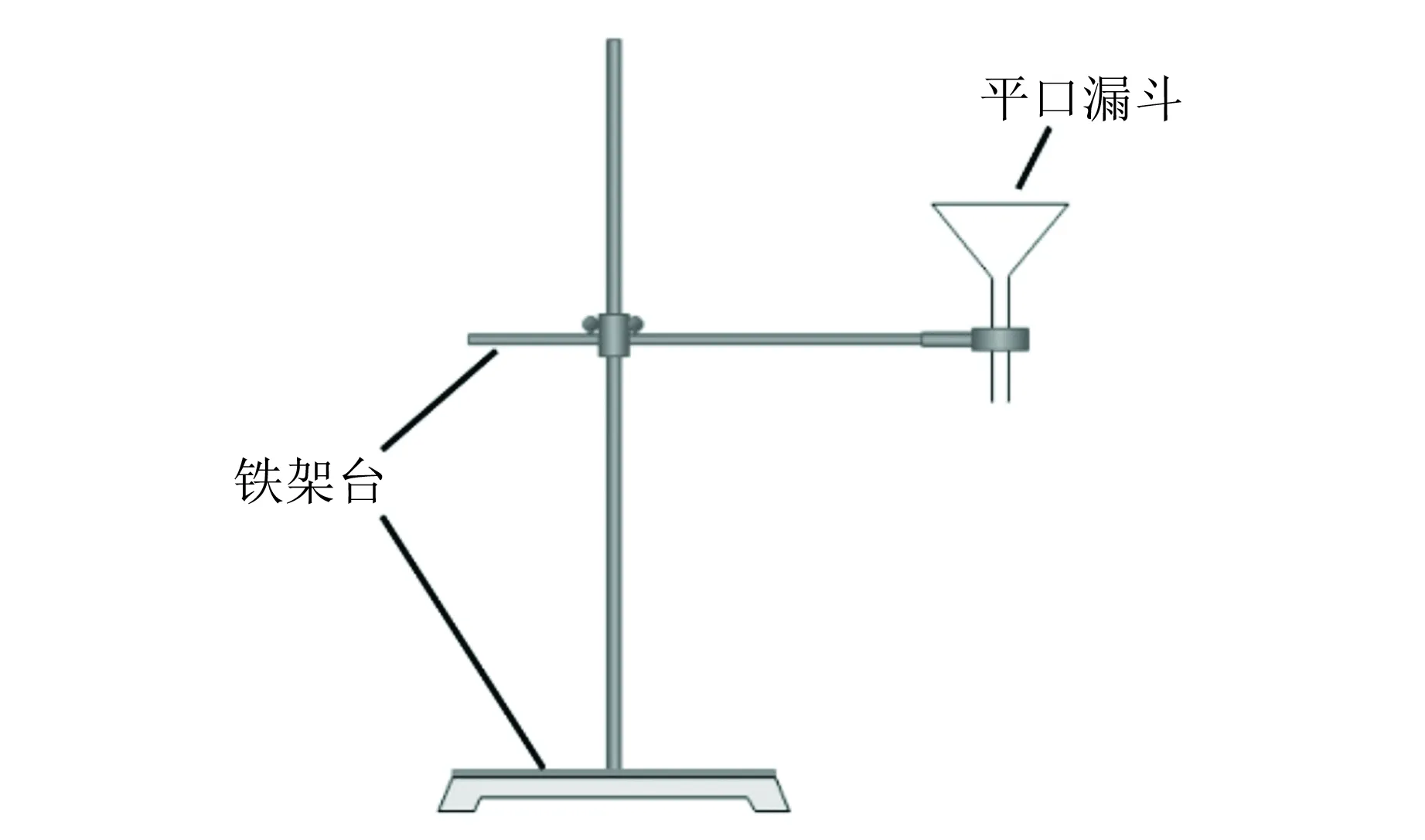
图3 实验装置

2.2 下落高度与形成的休止角的关系

使用直径为0.5 mm的白砂和直径为1.5 mm的小米[7-8],两者质量都为150 g,从85 mm的下落高度开始每50 mm进行实验测量休止角,实验结果用Matlab 2014a软件拟合分析. 多次实验后得到表1和表2中的数据.

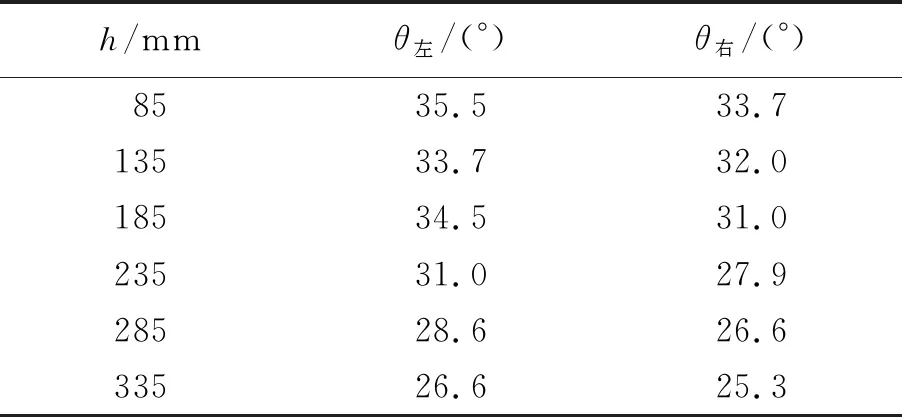
表1 使用白沙的下落高度与休止角数据

表2 使用小米的下落高度与休止角数据

图4～5为Matlab 2014a软件的拟合结果. 从图4～5可以看出,休止角随下落高度的增加呈非线性变化. 再从拟合结果可以得出结论:休止角θ随下落高度h的增加成反比的趋势.

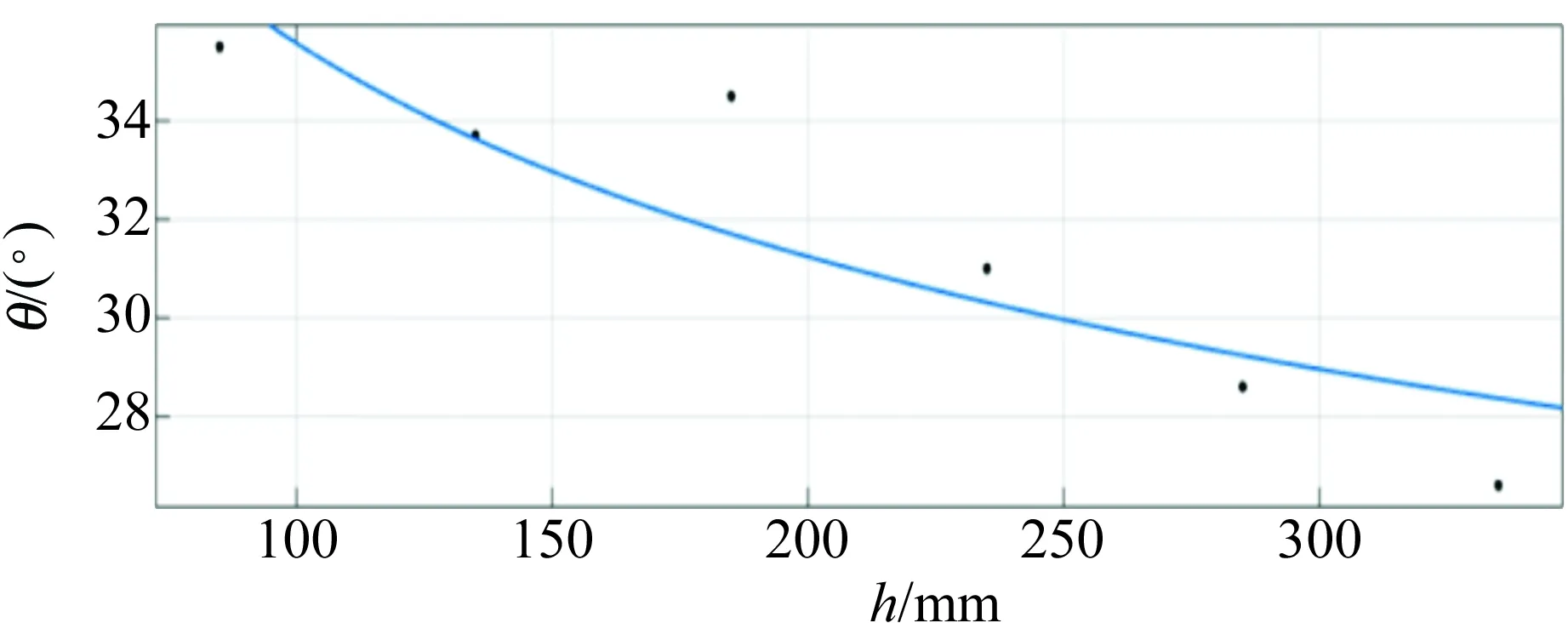
(a)左侧

(b)右侧图4 白沙的休止角

(a)左侧

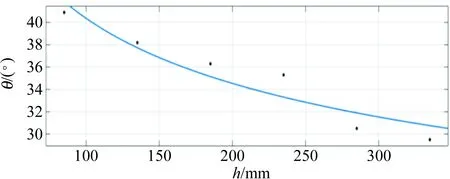
(b)右侧图5 小米的休止角

2.3 漏嘴口径与形成的休止角的关系

因为漏嘴过小时,小米不能自然流出,实验材料使用直径为0.5 mm的白砂,其质量为150 g. 采用的实验方法与之前相仿,倾倒的高度(即漏嘴与平面的垂直距离)为200 mm. 表3是不同漏嘴口径的实验数据,通过取差值的绝对值可以研究漏嘴口径对颗粒在不同母线上形成的休止角的影响. 图6是Matlab 2014a软件的拟合结果,从图中可以看出,休止角的差值|Δθ|随漏嘴口径r的增加成负相关的趋势.

表3 不同漏水口径的休止角

图6 休止角差值随漏斗口径的变化曲线

3 结 论

漏斗对于休止角也是重要的影响因素之一,本文研究了下落高度和漏嘴口径对休止角的影响. 在能形成休止角的情况下,下落高度影响了堆积结构与地面形成的休止角的大小,而漏嘴口径影响了在不同母线上休止角的大小. 从数据的拟合结果可以看出,下落高度与休止角成反比,漏嘴口径与休止角的差值的倒数成正比,仿真计算结果与实验结果相符.