对九脚探头磁导率、检测电压与应力相关性研究
魏 明,马占国,殷春浩,徐振坤
(1.中国矿业大学 a.深部岩土国家重点实验室;b.物理学院, 江苏 徐州 221116; 2. 徐州工程学院 数学与物理科学学院,江苏 徐州 221018 )
铁磁部件受到动静载荷的作用会产生应力集中,引起部件的局部疲劳、失效,如何快速有效地测量铁磁部件的应力分布,对锅炉、压力容器、起重机械等大型设备具有十分重要的意义[1-2]. 在应力作用下,铁磁部件被磁化时具有磁各向异性的特点,利用磁性探头的检测信号大小来反映磁各向异性强弱,从而判断铁磁部件的应力大小. 因此作为磁各向异性测量系统最重要部分的磁性探头,受到人们越来越多的关注,如何获得磁化强度大、稳定性强、功耗低的探头,成为目前研究的热点之一[3].
在磁测探头的研制和应用这一领域,R. Langman[4-5]在Π型两脚磁测探头的基础上,设计了可旋转的测量装置用于磁场检测,H. Yamada[6]等研究了四脚磁测探头磁路,K. Kashiwaya[7]等改进了四脚磁测探头,T. Isono[8]等在四脚探头的基础上,研制出了九脚探头的磁测传感器用于测量磁场强度. 石延平等设计了五脚[9]和六脚[10]差动式磁测探头,并与应变电测试验进行了比较. 赵洲等通过ANSYS模拟了九脚探头,得到了探头线圈距被测体不同距离的模拟图[11],并对九脚探头与二脚探头的实验结果做了比较,结果发现横向应力与纵向应力的测定结果相似,且分布趋势与焊缝处应力分布的理论定性分析基本吻合,初步验证九脚探头的测法理论分析的正确性[11]. 殷春浩、刘海顺等利用四脚探头和载荷实验机标定了应力感度曲线[12-13],研究了磁性探头测量间隙、探头阻抗与灵敏系数的关系,根据九脚探头不需要旋转的独特特点,提出磁输出信号与应力间的力学模型,建立了微观的磁通与宏观的电信号的关系[14-15].
1 九脚探头的检测电压与磁导率关系推导
T.Isono和S.Abukn等研制出九脚探头,其结构如图1所示,中间为励磁探脚,圆周8个探脚为感应探脚,l1为沿探脚方向的磁路长度,l2为感应探脚与励磁探脚间的磁路长度,S1为感应探脚横截面积,S2为中心励磁探脚的横截面积, 8个感应探脚同时与中间励磁探脚和被测材料形成闭合的磁路. 与传统探头相比,九脚探头与试件接触面积小[16],且测量应力比较小时探头无需转动即可测出该点的主应力差与主应力方向角,具有测试灵敏度高、测试系统简单等特点.
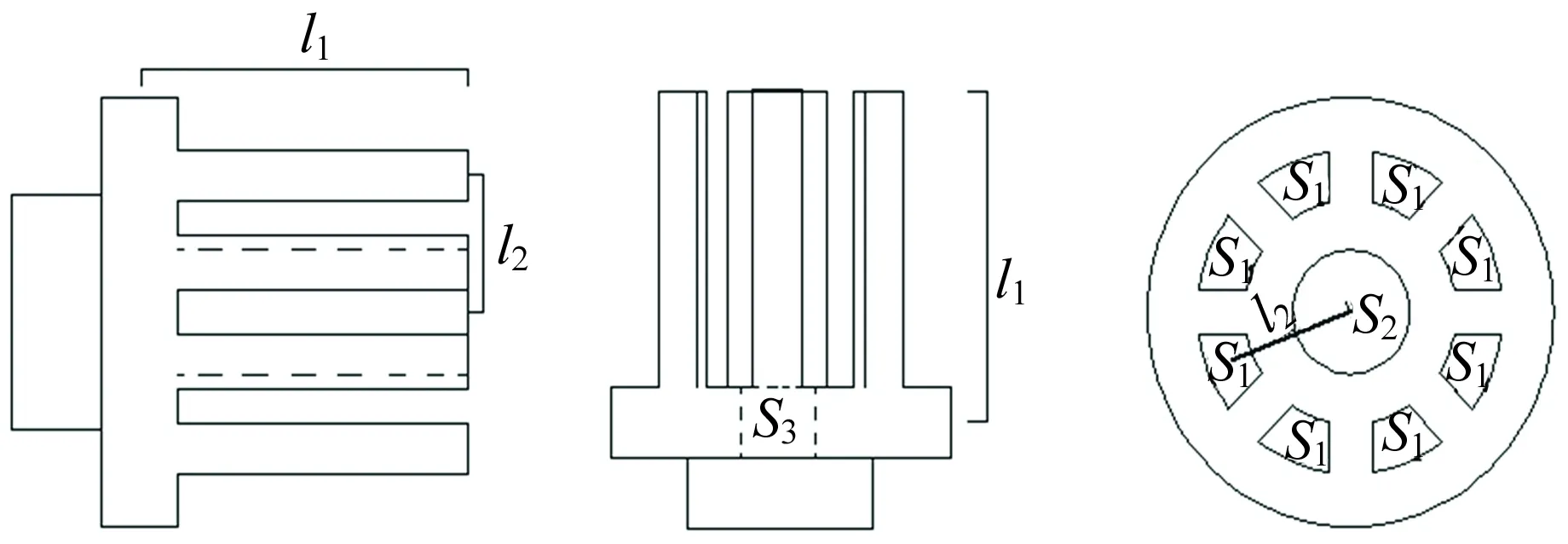
(a)侧视图 (b)俯视图图1 九脚探头的结构示意图
为了提高磁化强度和对样品磁化的均匀性,以四周8个探脚作为励磁探脚,中间探脚作为感应探脚. 当在励磁探脚上加载交流电流时,励磁线圈上产生交变的磁场和相应的磁动势Fm,在此作用下,励磁磁芯中会产生交变的磁通量Φm,Φm在探头和被测对象之间形成闭合磁回路,由磁路理论和基尔霍夫磁路定律可知
Fm=n1i,
(1)
磁阻为
(2)
式中,n1是励磁线圈的匝数,i是励磁线圈电流,l是对应的磁路长度.
在闭合的磁路中,磁动势Fm等于各部分磁压降(Hili)之和,即
(3)
又因为
(4)
把式(4)和式(2)代入到式(3)可得
(5)
式中μi,Si和li分别对应磁路的磁导率、横截面积和磁路长度.
因九脚探头总共有8个励磁探脚和1个感应探脚,每个励磁探脚都和感应探脚构成闭合的磁路,则检磁探脚的磁通量Φf可以表示为
(6)
根据法拉第电磁感应定律,检测线圈的感应电动势为
(7)
其中,n2为检测线圈的匝数,假设励磁电流i=Asin (ωt)(ω为角频率,A为电流幅值),则式(7)可以改写为
即便是习惯了网上买理财产品的客户,社区服务点的近距离、咨询式体验和传统的人际沟通同样可以起到较好的购买体验作用。
(8)
从而建立了检测线圈的感应电压ε(t)和磁导率μi的关系.
对于本实验,闭合磁路是由铁芯和被测材料2部分构成,因此,在对样品进行测量前需要确定探头的相对磁导率μr-t,然后再把探头的磁导率μr-t作为已知量来计算被测样品的相对磁导率μr-s.
实验中将感应电压ε(t)加载到RC积分放大器,则可以得到检测电压U同感应电压ε(t)的关系为
(9)
测量工频下的感应电压有效值εeff和检测电压Ueff的数据并作图,如图2所示.
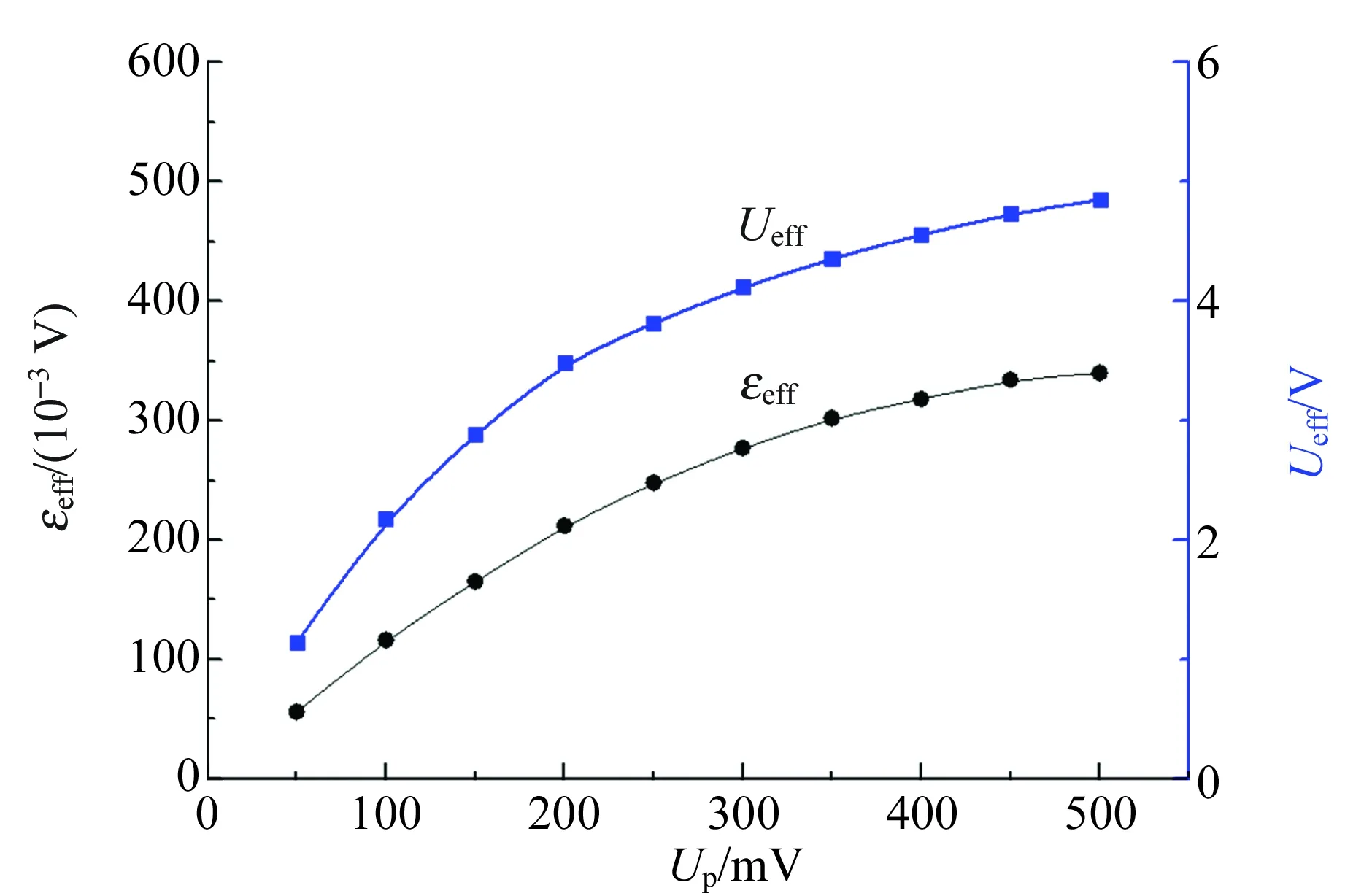
图2 50 Hz条件下的感应电压有效值εeff同检测电压有效值Ueff随励磁电压峰值变化的曲线图
通过拟合Ueff和εeff的关系曲线,得到
(10)
式中,α为对积分电路输入与输出数据的修正系数,α=1-0.000 64(Up-50),其中Up为励磁电压峰值.
(11)
其中
(12)
(13)
在式(13)中,探头的相对磁导率μr-t是未知量,Ueff为测量量,α为电路修正系数,其余为九脚探头的结构常量,因此可以计算出探头的相对磁导率μr-t. 测量九脚探头磁导率的示意图如图3所示.
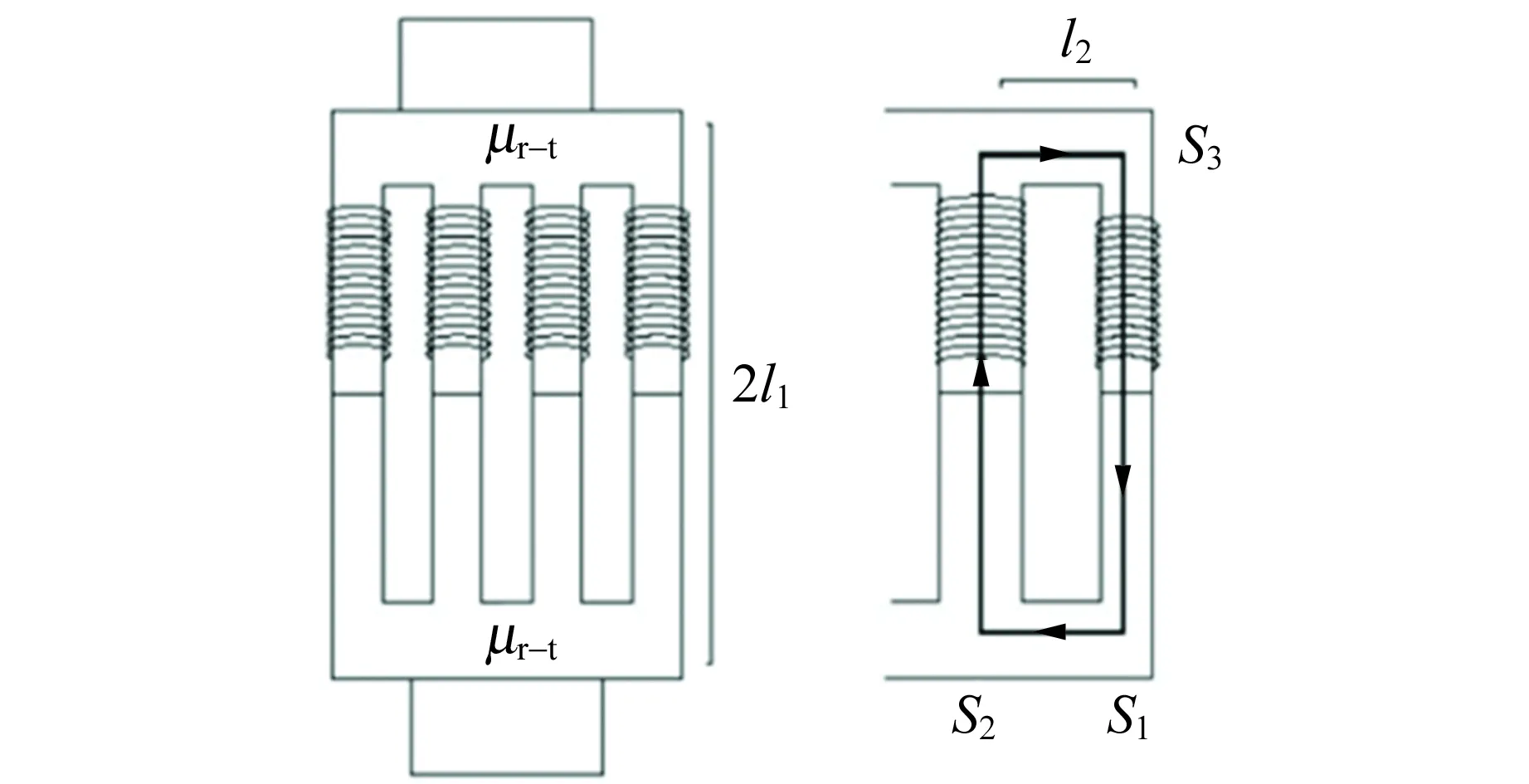
图3 九脚探头的磁导率测量示意图
在样品测试中,把被测的探头换成被测样品,图4为测量时的示意图,S4是被测材料部分的磁路横截面积,则有
(14)
被测材料的磁导率μr-s、铁芯相对磁导率μr和样品检测电压Us-eff之间的关系为
(15)
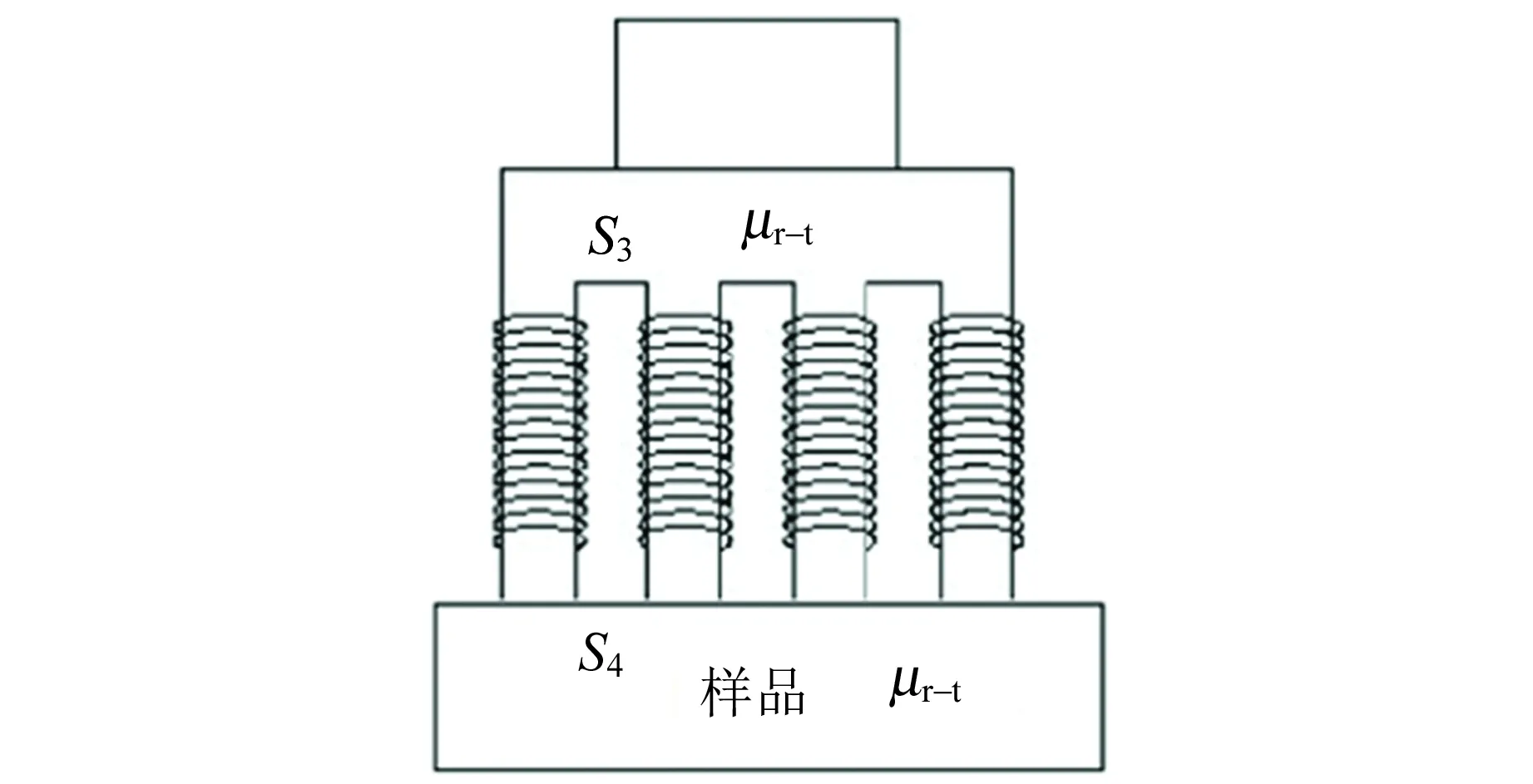
图4 样品的磁导率测量示意图
把探头的磁导率μr-t代入到式(15),并结合九脚探头和电路的参量可得到被测样品的μr-s.
2 实验结果与分析
实验采用静载拉伸的方式,对Q235,Q255,Q345#进行拉伸实验,样品尺寸按照GB/T 6397-1986的标准,按照50 MPa的步进方式进行实验测试,并记录了不同拉力下,磁导率的检测电压差值随着励磁电压的变化曲线图,如图5所示.
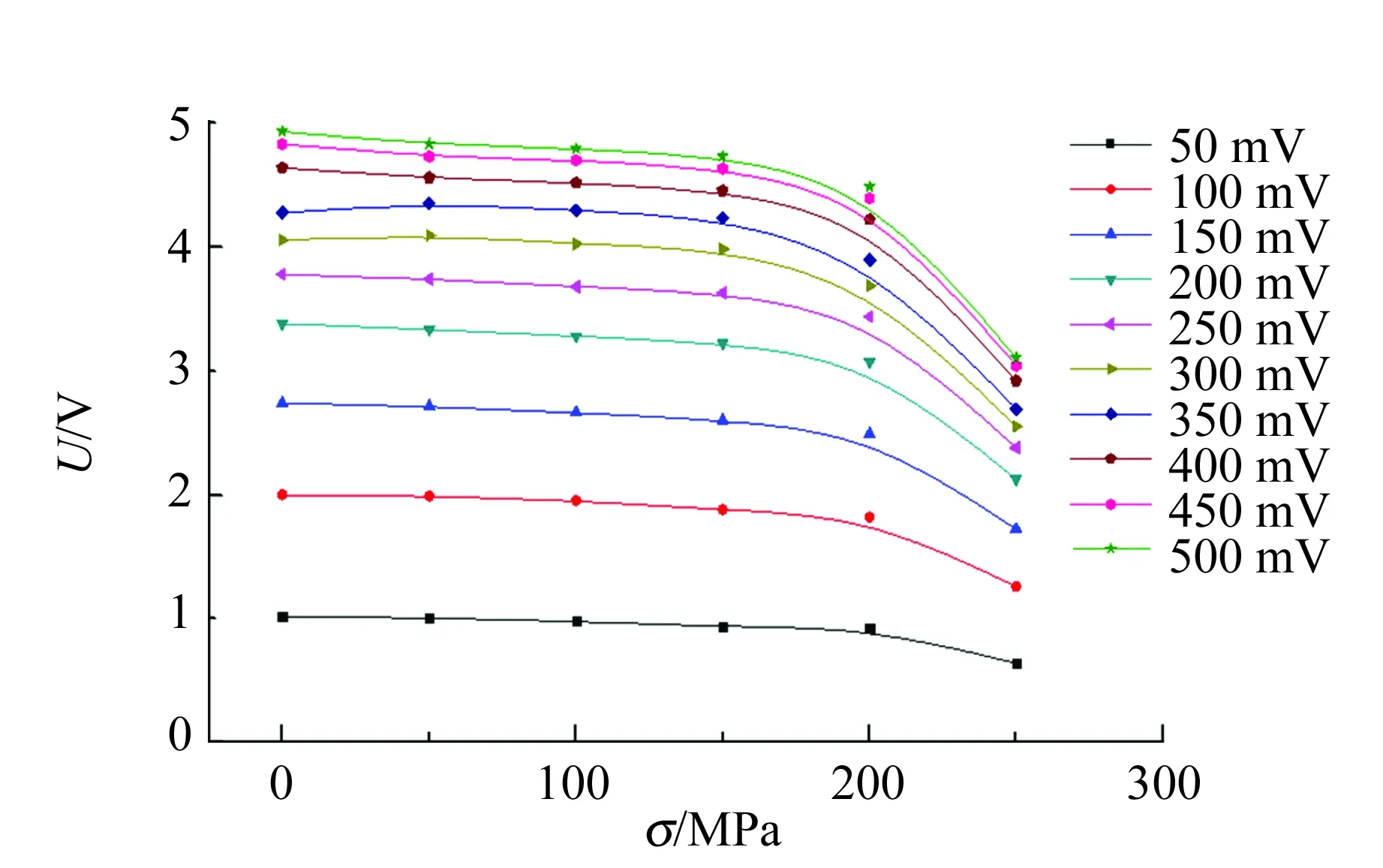
(a)Q235
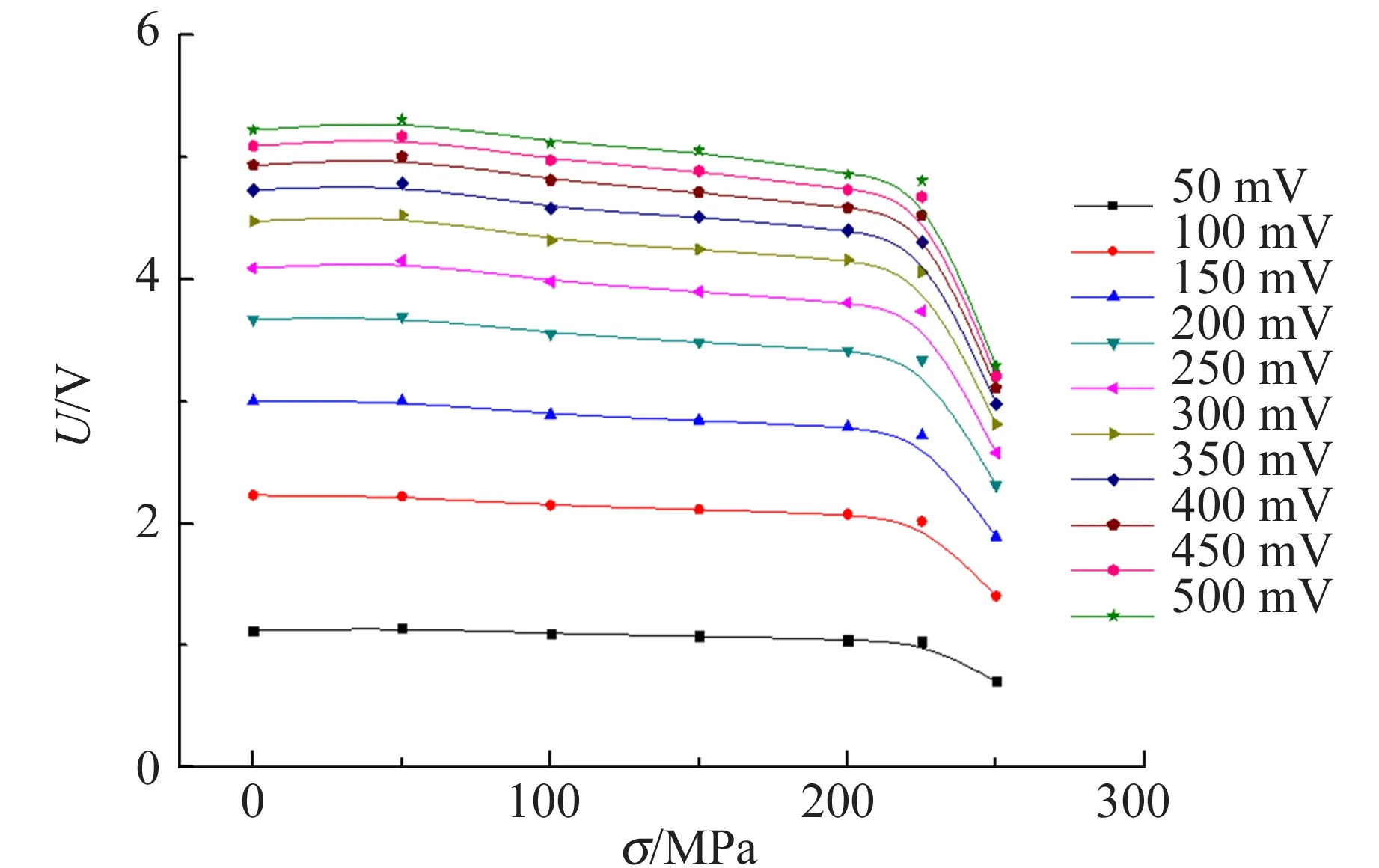
(b)Q255
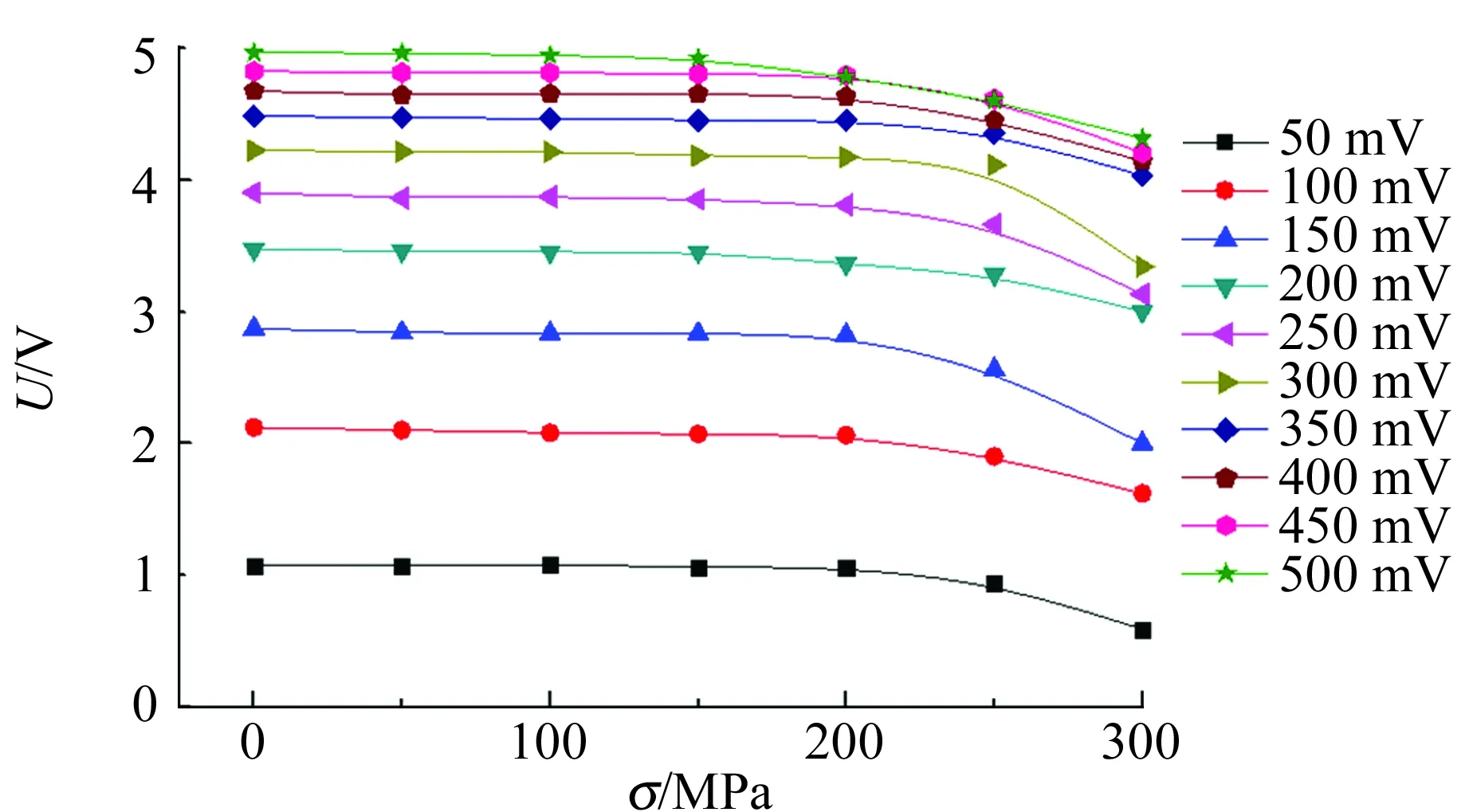
(c)Q345图5 不同应力条件下,磁导率的检测信号与0 kN应力条件下的差值随励磁电压变化的关系曲线
从图5中可以看出,在相同的应力条件下,随着励磁电压的升高,探头的检测电压也升高,但升高的幅度会随着逐渐减小,在50~200 mV之间,检测电压幅值增加较大,励磁电压大于200 mV后,检测电压幅值增加越来越小,并趋于稳定. 从样品磁化的角度分析,励磁电压的大小代表励磁磁场的大小,励磁电压越大,磁场强度越大,在样品未饱和磁化前,样品的磁化强度会随着励磁磁场的增加而快速增加,当样品磁化强度趋于饱和时,样品的磁化强度随着励磁磁场的增加而缓慢增加.
在样品在相同的励磁电压的条件,即相同的励磁磁场下,九脚探头的检测电压随着应力的增加而呈现出减小的趋势,Q235,Q235和Q345样品的输出电压随应力增加而减小的趋势较为明显,3个样品的输出电压整体呈现出减小的趋势,但中间过程存在小的波动. 从图5中可以看到,在样品没有达到屈服之前,样品的输出电压几乎随着应力的增加呈线性递减,当样品接近屈服状态或者外应力超过屈服应力时,样品的输出电压递减较快,呈现非线性变化的特点.
分析其原因如下:当样品未受力和未被磁化前,样品对外不显磁性,当样品在应力和局部磁化的作用下,样品内部的磁畴沿着外磁场方向偏转,磁畴取向的变化导致样品磁化方向的变化,导致检测线圈的磁通量的变化产生感应电压,在初始磁化时,样品内部磁畴的取向由随机取向逐渐转变为沿外磁场方向,导致样品的磁通量变化量ΔΦ随励磁电压的增加而快速的增加,即ΔΦ/ΔU较大,导致检测电压在样品初始磁化时随励磁电压增加而快速增加;当样品内部磁化逐步达到饱和状态,导致检测线圈的磁通量变化量随励磁电压的变化量的增幅变慢,即ΔΦ/ΔU降低,从导致检测电压的增幅变缓. 另一方面,样品在弹性形变区域内,检测电压随应力的变化很小,几乎接近于线性变化的关系,但在拉应力接近屈服应力时,检测电压大小随应力的增加而快速减小.
3 结 论
与传统探头相比,九脚探头与试件接触面积小,励磁探脚关于中心对称分布,能够产生更强、更均匀的励磁磁场,提高了实验精度和实验效率. 利用九脚探头测试了Q235,Q255和Q345#钢材在不同应力条件下的检测电压随励磁电压变化的曲线,实验表明,在相同的励磁电压条件下,应力达到试件的屈服点之前,探头的检测电压同应力呈线性关系,当应力接近屈服点时,检测电压随应力增加而快速变小,呈非线性关系. 利用该特点,可以快速检测工程中的铁磁部件受力状态.

