矩形舱内三层液体晃荡特性的数值分析

刘东喜， 庄宿国， 王 晋， 尤云祥

(1. 上海海事大学 海洋科学与工程学院， 上海 201306； 2. 西安航天动力研究所， 西安 710100； 3. 上海交通大学 海洋工程国家重点实验室， 上海 200240)

随着能源需求的不断增长和近海油气资源的日益减少，海洋油气开采逐渐向深海区域发展，越来越多的浮式平台投入使用.为进一步提高浮式生产储卸油(Floating Production Storage and Offloading，FPSO)装置的生产效率，国外石油公司提出在船体内安装大型清洗舱以作为传统油-气-水分离器的预处理设备.与分离器一样，清洗舱内油层与水层之间也存在一定厚度的乳化层.在风、浪、流等海洋环境载荷的共同作用下，FPSO装置将会产生6个自由度的运动，从而导致平台清洗舱内多层液体的晃荡.

目前，国内外对多层液体晃荡现象的研究主要采用数值模拟和模型试验的方法.王日新等[1]采用标记网格(Marker and Cell，MAC)方法对纵摇激励下矩形舱内两层液体的晃荡情况进行了数值模拟；Xue等[2]采用流体体积(Volume of Fraction，VOF)方法和试验方法研究了矩形舱内油层与水层液体的晃荡问题；Molin等[3]采用线性势流理论方法和试验方法研究了FPSO装置矩形清洗舱内三层液体的晃荡情况；Kim等[4]等采用一种改进的移动粒子半隐式(Moving Particle Semi-implicit，MPS)方法模拟了矩形舱内三层液体的晃荡问题.但是，与传统的单层液体晃荡问题相比，多层液体晃荡问题的相关研究成果还较少，有待进一步深入研究[5].

本文采用Sussman等[6]提出的耦合水平集和流体体积 (Coupled Level Set and Volume of Fluid, CLSVOF)界面捕获方法对FPSO装置矩形清洗舱内三层液体的晃荡特性进行数值模拟.开展了自由衰减测试试验，得到了自由表面和两个液-液界面的固有频率，研究了液-液界面产生的Kelvin-Helmholtz不稳定性，同时，通过对比模拟与试验所得界面形状和界面高度的变化情况，从而验证了所用数值模拟方法的准确性.

1 晃荡问题描述

本文采用的矩形舱内三层液体晃荡算例由Molin等[3]提供.矩形舱系统模型如图1所示，其中，坐标x、y和z轴方向分别表示矩形舱长度方向、高度方向和宽度方向.矩形舱的长度、高度和垂直纸面宽度分别为 1.08、0.90 和 0.10 m.舱内充装三层互不相溶的液体，其物理性能参数见表1.表中：ρ为密度；ν为运动黏度；σ为表面张力系数.

根据线性势流理论计算可得图1中自由表面、C-W界面和W-D界面的共振晃荡频率.对于某二维矩形舱内多层液体系统，矩形舱长度为L，舱内充装三层液体，其厚度和密度分别为he和ρe(e=1，2，

图1 矩形舱内三层液体的晃荡模型(m)Fig.1 Schematic model for three-layer liquid sloshing in a rectangular tank (m)

液体ρ/(g·cm-3)ν/(mm2·s-1)σ/(mN·m-1)二氯甲烷1.300.327.8水1.001.072.7环己烷0.781.324.7

3)，且ρ1>ρ2>ρ3.令上述线性系统的无阻尼矩阵行列式等于0，则行列式可表示为固有频率ω的6阶多项式，即[3]

Ψ6ω6+Ψ4ω4+Ψ2ω2+Ψ0=0

(1)

(2)

(3)

式中：g为重力加速度；n为模数.

2 数值模型

矩形舱内流体运动的控制方程为连续方程和动量方程，即

(4)

(5)

式中：下标i、j为x轴的方向；ui、uj分别为xi、xj方向的速度；p为压力；fi为外部加速度；Fi为表面张力.

采用Sussman等[6]提出的CLSVOF方法分析三层液体晃荡过程中的自由表面和液-液界面的运动特性.其中：VOF方法是通过在每个计算单元上定义一个体积分数α来实现界面追踪的，且α=0表示该单元被上层流体充满，α=1 表示该单元被下层流体充满，0<α<1 表示界面跨过该单元；水平集方法是通过定义等值函数φ来实现对液-液界面追踪的，且φ=0处为界面，某一点的φ值为该点到界面的距离，φ<0表示界面上层流体，φ>0表示界面下层流体.函数φ和α的输运方程为

(6)

为避免流体物理性能在界面出现间断，引入一个光滑的Heaviside函数H(φ)以对界面很小范围内的流体物理性能进行连续化处理，H(φ)的形式为

H(φ)=

(7)

式中：h为网格尺寸.密度和黏度的控制方程为

ρ(φ)=ρaH(φ)+ρb[1-H(φ)]

(8)

μ(φ)=μaH(φ)+μb[1-H(φ)]

(9)

式中：下标b和a分别为上层和下层流体. 界面法向向量n和曲率κ(φ)的计算公式如下：

ni=∂φ/∂xi

(10)

(11)

式中：xk表示k方向分量.

Funada等[7]发现，表面张力对界面不稳定性以及界面短波的影响显著.本文采用CSF(Continuum Surface Force)模型[8]计算表面张力，即

(12)

函数δ(φ)可通过对H(φ)求导得到，即

(13)

为了精确求解，必须始终保持φ为距离函数，即|∂φ/∂xk|=1，但是经过几步的计算后，φ将不再满足距离函数的条件.在保持界面位置不变的情况下，需要重新构造等值函数φ.

3 自由衰减测试

为得到自由表面和两个液-液界面固有频率的数值模拟值，本文进行了自由衰减测试，并通过模拟值与理论值的对比来初步验证数值模拟方法的准确性.根据图1中矩形舱模型的尺寸和三层液体的充装高度，采用网格划分软件ICEM生成一组单元数为 77.76 万的三维精细网格系统.计算时间步长设定为 0.5 ms.计算开始之前，将矩形舱内自由表面和两个液-液界面初始化为倾斜状态，倾斜幅度为5°；计算开始之后，三层液体将在重力作用下做自由振荡；计算过程中，实时记录舱壁处3个界面高度的变化数据.由于根据线性势流理论方法(式(1)～(3))得到的固有频率没有考虑流体黏性，所以本文的自由衰减测试也假设流体为无黏性流体.图2示出了距离矩形舱左侧舱壁5 mm处3个界面的高度变化曲线对应的频谱密度P.图中，谱密度峰值对应的频率即为固有频率.

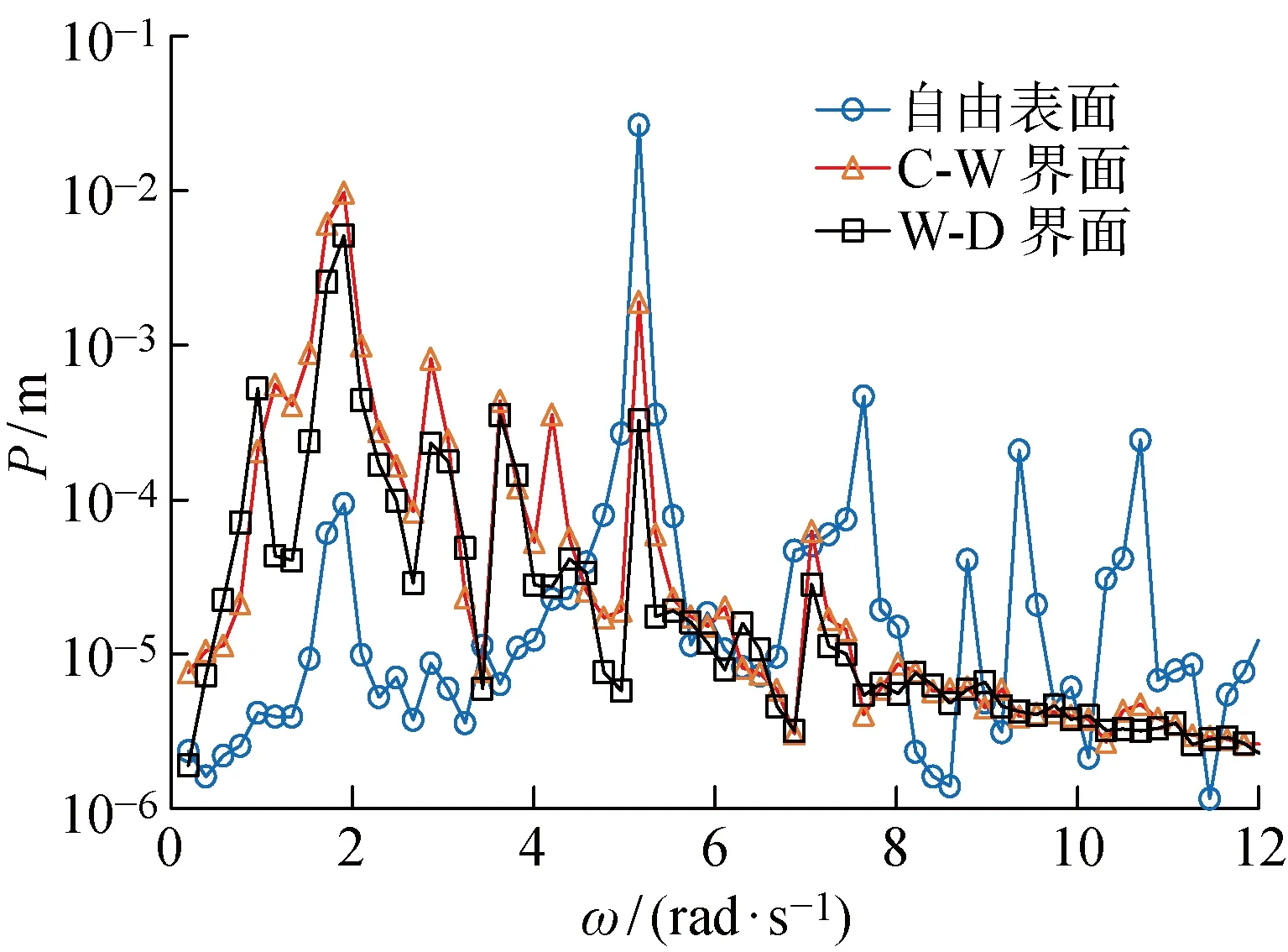
图2 自由表面和液-液界面高度的频谱密度Fig.2 Power spectrums of free decay of sloshing waves

Tab.2 Simulated and theoretical values of natural frequencies of the first four sloshing modes

模态阶数ωsim/(rad·s-1)自由面C-W面W-D面ωcal/(rad·s-1)自由面C-W面W-D面15.1561.9090.9555.2041.8381.05027.6392.8651.9097.5502.9491.98639.3573.6282.8649.2523.6082.775410.6944.2013.62810.6804.0803.436

表2列出了前4阶模态晃荡固有频率的自由衰减数值模拟值(ωsim)和线性势流理论计算值(ωcal).可以看出，其模拟值与理论值吻合良好，初步验证了本文所采用的数值模拟方法的准确性.

4 结果与分析

舱体绕z轴做受迫横摇运动，其运动方程为θ(t)=θesin(ωet)，θ为矩形舱的横摇角度，θe=1° 为横摇角的幅值，ωe=1.83 rad/s为激励频率.由表2可知，该激励频率等于中部C-W界面的最低阶固有频率.

图3示出了矩形舱左侧舱壁处顶部自由表面、中部C-W界面和底部W-D界面高度随时间的变化曲线.可以看出：当激励频率等于中部C-W界面的最低阶固有频率时，C-W界面和W-D界面在振荡初期出现了共振，约20个振荡周期后，其运动趋于稳定；C-W界面的运动幅度明显大于另外两个界面，该结果符合预期；W-D界面与C-W界面的振荡频率相同，但其振荡幅值小于C-W界面；自由表面的运动幅度较弱，振荡幅值远小于另外两个内部界面，故其振荡相位也稍微偏离另外两个内部界面；另外，W-D界面高度的变化曲线呈现出峰宽谷窄的特征，且峰值明显小于谷值，该现象与非线性自由表面波的特征相反.

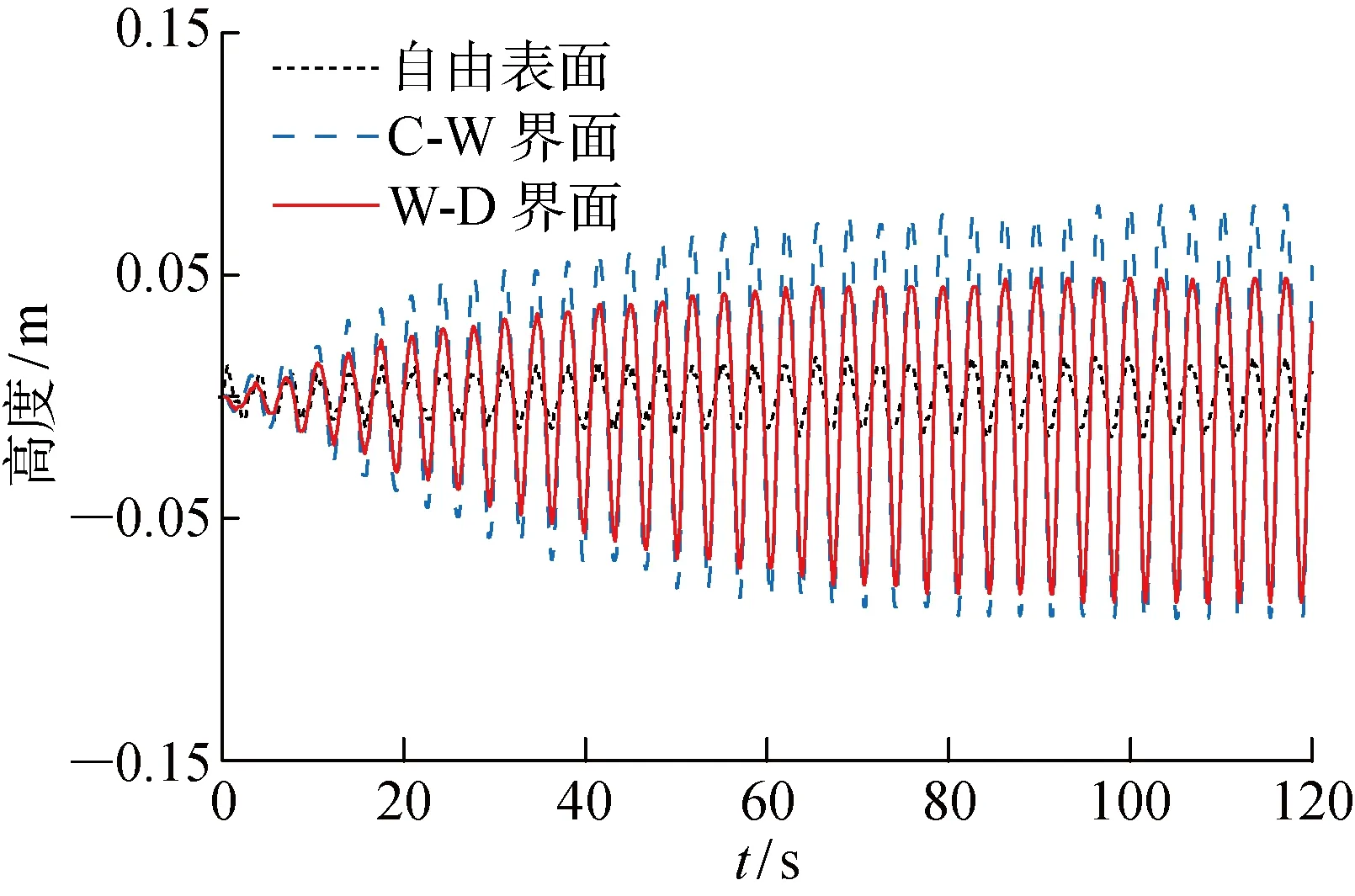
图3 左侧舱壁处自由表面和液-液界面的高度变化曲线Fig.3 Elevation time history of three interfaces at left wall of the tank

图4 左侧舱壁处界面高度时程的计算值与试验结果对比Fig.4 Comparison of elevation time history at the left wall by simulation and test results

图5 自由表面和液-液界面形状的计算与试验结果对比Fig.5 Comparison of two interfaces obtained by simulation and test

图4所示为左侧舱壁处3个界面高度时程的计算结果与Molin等[3]的试验结果对比.可以看出，计算值与试验值吻合良好，从而进一步验证了本文所用数值模拟方法的准确性.需要说明的是，试验所得 W-D 界面高度的变化曲线中出现的上、下抖动可能是由于传感器失效等测量误差造成的.图5示出了两个不同时刻的自由表面和液-液界面形状的计算结果和试验结果.可见两者吻合良好.内部界面晃荡运动的幅度远大于顶部自由表面.另外，由于上述激励频率等于中间层液体的最低阶固有频率，且接近于底层液体的2阶固有频率，所以由图5可以观察到中部C-W界面的1阶模态和底部W-D界面的2阶模态.

Funada等[7]指出，当两种流体的交界面出现切向速度间断时，流体界面是不稳定的，将会产生Kelvin-Helmholtz不稳定性.在这种不稳定性的作用下，流体界面产生的小扰动经过线性和非线性的增长后会在强的非线性作用下发展成湍流混合.当激励频率接近于矩形舱多层液体系统某一液-液界面的最低阶固有频率时，界面的大幅度共振运动将会导致界面出现Kelvin-Helmholtz不稳定性.图6示出了t=96.3 s时由Kelvin-Helmholtz不稳定性所致C-W界面出现的锯齿状短波，该现象进一步表明多层液体晃荡问题比单层液体晃荡问题复杂得多.同时，图6对比了C-W界面Kelvin-Helmholtz(K-H)不稳定性的数值模拟结果与Molin等[3]的试验结果.由图6中界面锯齿波的形状以及相应的短波长度来看，本文的模拟结果与试验结果非常接近，表明本文所用数值模拟方法不仅能够准确预测液-液界面的整体晃荡行为(界面晃荡运动)，而且能够准确预测液-液界面的小尺度物理现象(K-H不稳定性).

图6 C-W界面K-H不稳定性的数值模拟与试验结果对比Fig.6 Comparison between numerical solution and test results of K-H instability at the C-W interface

5 结语

本文采用CLSVOF界面捕获方法对FPSO装置矩形清洗舱内三层液体的晃荡特性进行了数值分析，并将模拟结果与试验结果进行对比.结果表明，多层液体储卸舱系统存在不止一种晃荡固有频率.当清洗舱外部激励频率接近于液-液界面的最低阶固有频率时，将产生共振效应并导致液-液界面的晃荡幅度远大于自由表面，表明即使清洗舱的受迫运动幅度不大，但只要发生内部共振，大幅度的内部晃荡运动也会明显降低其分离性能.因此，在设计多层液体储卸舱系统时，不仅要考虑顶部自由表面的运动特性，而且要考虑内部界面的运动特性.另外，共振效应也会导致液-液界面出现复杂的锯齿状短波.所用CLSVOF方法不仅能够预测自由表面和液-液界面的大尺度整体晃荡行为，而且能够表征液-液界面出现的小尺度物理现象，适用于多层液体晃荡特性的数值分析.