锐钛矿型TiO2纳米管拉伸性能的分子动力学研究

杨 康，杨 亮，林仕伟

(海南大学 材料科学与工程学院，海南 海口 570228)

0 引 言

TiO2纳米管以其独特的物理、化学及生物学性质已经被广泛地应用于光催化反应[1-2]、气敏传感性[3-4]、染料敏化电池[5]、生物材料[6]及储氢材料[7]等领域。目前，TiO2纳米管的制备方法主要有水热合成法[8]和电化学阳极氧化法[9]两种方法，以上两种方法制备纳米管的机理不同，制备获得的纳米管结构差异较大，水热合成法制备的TiO2纳米管为单壁晶体结构，而阳极氧化法制备的TiO2纳米管为大壁厚的无定型结构。TiO2主要存在三种结晶形态：锐钛矿型、金红石型和板钛矿型[10]，其中锐钛矿型TiO2的光催化性能更为突出。TiO2纳米管广泛应用于各种传感器和电器件中，为满足器件的性能需要良好的物理化学性质，其中也包括力学性质。不同方法制得的纳米管结构各不相同，纳米管手性方向也相差很大，因此实验中单个纳米管的力学性能就很难准确地测出，而采用密度泛函理论或者分子动力学等计算手段能够有效地预测材料的力学性能[11]。

本文将锐钛矿型(101)表面的单周期片层材料沿不同手性方向进行卷曲成单周期TiO2纳米管状结构，利用分子动力学方法模拟不同手性角TiO2纳米管随温度变化的力学规律，并对不同手性角与力学性质的关系进行预测，从原子尺度提供微观结构与力学性质的相互关系，希望对实验研究及实际应用做理论指导。

1 建立模型

两端开口的单壁TiO2纳米管可以看作是锐钛矿(101)表面(图1)的一个矩形无缝卷曲而成的管状结构，并使用卷曲矢量来表征，是对应纳米管横截面的周长，其表达方式为：

为了使计算规律更加普适可信，本文计算典型手性角的TiO2纳米管(图2)，其手性指数分别取(0，9)，(8，16)，(10，10)，(10，5)，(18，0)。

图1 锐钛矿(101)晶面和纳米管的卷曲方向Fig.1 Anatase (101) lattice and rolling-up directions of the nanotubes

2 计算方法

LAMMPS(Large-scale Atomic/Molecular Massively Parallel Simulator)[12]是由美国国家能源部下的Sandia国家实验室开发基于牛顿力学的经典分子动力学模拟的开源软件。分子动力学计算结果强烈依赖所采用的势函数的精度，本计算选用物理意义明确的，经典的对势表达式形式的势函数，该势函数是由Matsui和Akaogi提出的MA势函数[13-14]，MA势函数的表达式如下：

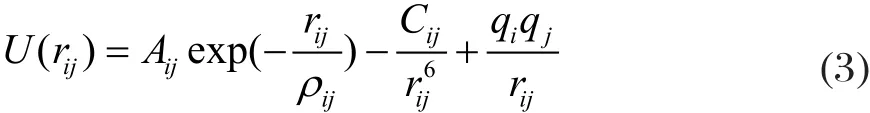
其中，U(rij)是原子间相互作用势，rij代表原子i和j之间的距离。氧原子和钛原子所带电荷分别为-1.098 e和+2.196 e，势函数参数详见表1。为了在100 K、500 K、1000 K、1500 K、2000 K和2500 K温度恒定条件下计算纳米管的拉伸情况，采用周期性边界条件NPT系综下对纳米管进拉伸模拟，时间步长为1 fs，总模拟时长200 ps。

表1 MA势函数的相关参数Tab.1 Parameters of MA potential function

图2 锐钛矿型TiO2纳米管不同手性结构示意图。红色原子为氧原子，蓝色原子为钛原子Fig.2 Different chiral structures of anatase-type TiO2 nanotubes. The red atom is the oxygen atom, and the blue atom is the titanium atom

3 结果分析

3.1 温度与抗拉强度的关系

图3 锐钛矿(101)横向视图，原子下标表示其配位数Fig.3 A cross view of anatase (101) sheets. The subscript of an atom represents its coordination number

图4 TiO2纳米管拉伸形变应力-应变曲线,手性角分别为(a)θ = 36.49°，(b)θ = 10.47°，(c)θ = 20.29°，(d)θ = 90°，(e)θ = 0°以及不同手性角的TiO2纳米管抗拉强度-温度关系图Fig.4 Tensile deformation stress-strain curves of TiO2 nanotubes with the chiral angle (a) θ = 36.49°, (b) θ = 10.47°, (c) θ = 20.29°, (d) θ = 90°,(e) θ = 0° and TiO2 nanotube tensile strength-temperature diagrams of different chiral angles

通过计算不同手性角的TiO2纳米管随温度变化的应力-应变关系，结果如图4所示。计算结果表明：手性角为θ = 36.49°和θ = 0°的TiO2纳米管的拉伸强度随着体系温度的升高，抗拉强度按指数衰减。而手性角θ = 10.47°，θ = 20.29°和θ = 90°的TiO2纳米管的抗拉强度随温度的升高呈现先减小后增大的趋势，其中当θ = 10.47°和θ = 20.29°时，抗拉强度在1500 K左右出现最小值，而θ = 90°时，抗拉强度的最小值出现在1000 K左右。

3.2 结构分析

通过研究不同手性角在100 K的拉伸结构变化情况，获得不同应变量下纳米管结构的微观变化规律。结果如图3和图5所示，手性角θ = 36.49°的纳米管拉伸后Ti6C-O3C键最先发生断裂，基本的TiO2纳米管结构单元发生严重的断裂变形；手性角θ=10.47°的纳米管拉伸后Ti5C-O3C键最先发生断裂并呈现类螺旋结构；手性角θ = 20.29°的纳米管拉伸后Ti5C-O3C键最先发生断裂并呈现层状堆叠结构，但层与层之间的原子并不是完全对等，而相差一定的角度，所以整体来看整个纳米管还呈现螺旋结构；手性角θ = 90°的纳米管拉伸后Ti5C-O3C键最先发生断并呈现单环分层结构；手性角θ = 0°的纳米管拉伸后同时有Ti5C-O2C键、Ti6C-O2C键和Ti6C-O3C键发生断裂并呈现类似单环分层的结构，从图5(e)中可看出钛原子和氧原子分别构成单环，但不是所有原子处在环平面上。通过以上比较发现θ = 36.49°和θ = 0°的纳米管均先出现了Ti6C-O3C键的断裂，其抗拉强度按指数衰减，其余三个手性方向的纳米管均表现出有Ti5C-O3C键的断裂引起抗拉强度先增大后减小，由此可以推测纳米材料不同键的断裂对抗拉强度有直接的影响。

材料的物理化学性质由材料的相结构直接决定，尤其对于氧化物表现更加明显。纳米管拉伸过程中，纳米管的基本结构单元在外力作用下随应变量的变化发生不断变化，因此可考察简单立方、面心立方、体心立方和密排六方相结构在纳米管的演化过程中的比例变化来定性研究抗拉强度变化与相结构的相应关系。各结构的比例可通过开源软件Ovito进行分析获得。

表2统计数据可以看出，随着温度的上升，手性角θ = 36.49°的TiO2纳米管中Simple cubic的平均比例从30%增加到了35%，FCC、BCC和HCP的比例从0%逐渐增加，且随温度变化HCP占比与BCC和FCC占比的总和相差不大。

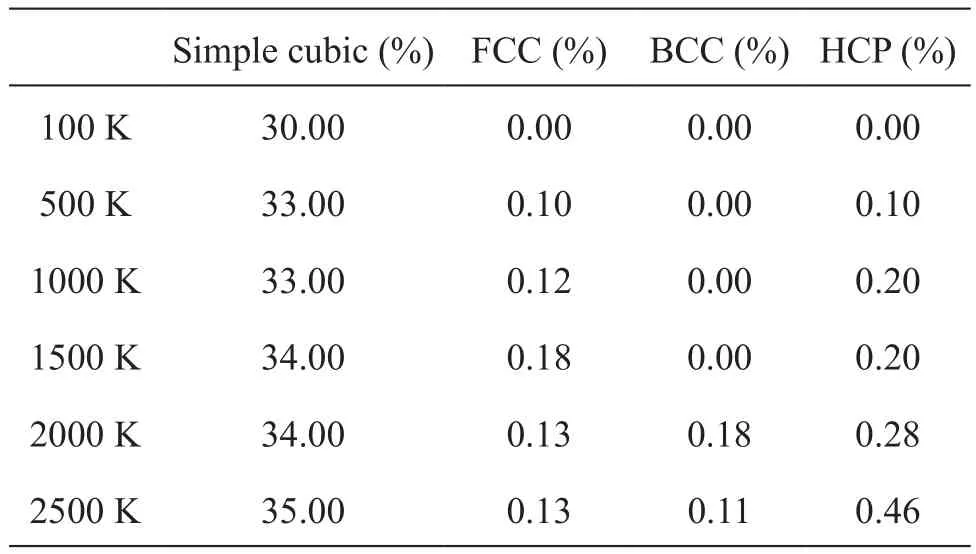
表2 手性角θ = 36.49°纳米管的空间点阵比例随温度的变化Tab.2 Variation of spatial lattice ratio of nanotubes at chiral angular θ = 36.49° with temperature

图5 手性角分别为(a)θ = 36.49°，(b)θ = 10.47°，(c)θ = 20.29°，(d)θ = 90°，(e)θ = 0°纳米管初始状态以及拉伸后对应的状态Fig.5 When the chiral angles are (a) θ = 36.49°, (b) θ = 10.47°, (c) θ = 20.29°, (d) θ = 90°, and (e) θ = 0°, the initial state of the nanotubes and the corresponding state after stretching

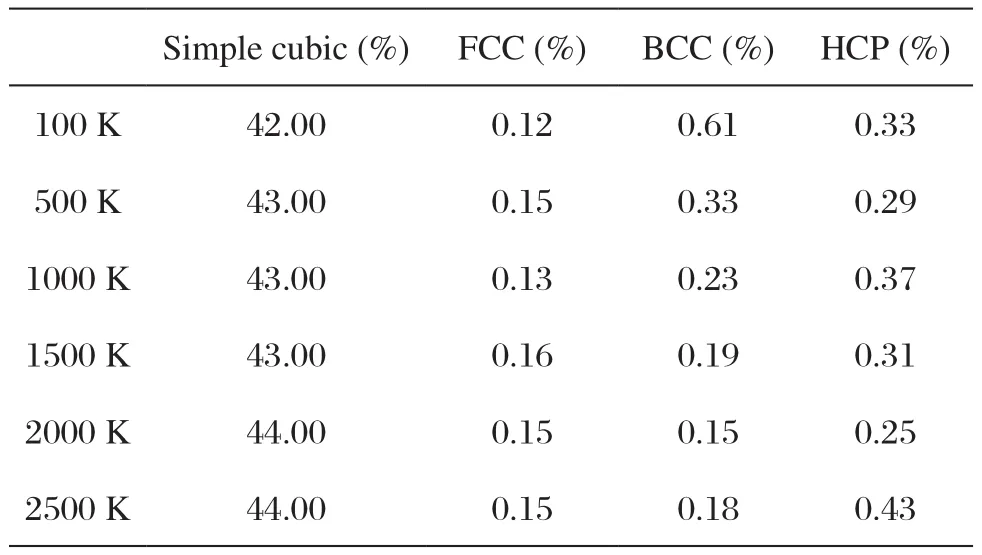
表3 手性角θ = 0°纳米管的空间点阵比例随温度的变化Tab.3 Variation of spatial lattice ratio of nanotubes at chiral angular θ = 0° with temperature

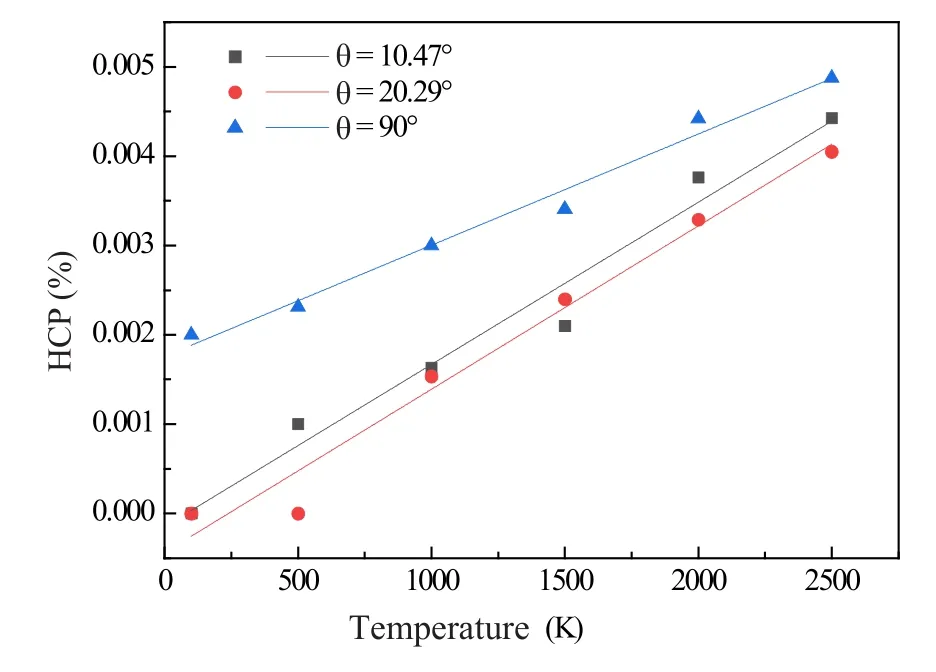
图6 手性角θ = 10.47°、θ = 20.29°和θ = 90°纳米管HCP比例与温度的关系Fig.6 Relationship between the HCP ratio of nanotubes at chiral angle θ = 10.47°, θ = 20.29° and θ = 90° to temperature

表3统计数据可以看出，随着温度的上升，手性角θ = 0°的TiO2纳米管中Simple cubic的平均比例从42%增加到了44%，HCP的比例上下波动，BCC的比例逐渐减少。与θ = 36.49°的TiO2纳米管相似，拉伸过程中HCP占比与BCC和FCC占比的总和低约0.1%，并且还出现了BCC和FCC占比的总和大于HCP的占比。

从图6可以看出，随着温度的升高，手性角分别为θ = 10.47°、θ = 20.29°和θ = 90°的纳米管拉伸过程中HCP所占纳米管的比例呈一定线性逐渐增加，Simple Cubic、FCC和BCC的占比与表2类似。HCP占比与BCC和FCC占比的总和高约0.1%。

由上述分析可以得知，相结构的不同对抗拉强度有明显的影响。随着温度的上升，HCP占比较大的TiO2纳米管抗拉强度表现为增强效果；而BCC和FCC与HCP的占比相差不大时，抗拉强度表现为逐渐减小。

4 结 论

(1)本论文通过分子动力学对不同手性的TiO2纳米管拉伸性能的研究表明纳米管的抗拉强度随温度变化规律不同。手性角θ = 36.49°和θ = 0°的纳米管随温度升高，抗拉强度按指数衰减；手性角分别为θ = 10.47°、θ = 20.29°和θ = 90°的纳米管随温度升高，抗拉强度先减小后增大。

(2)TiO2纳米管抗拉强度变化规律由微观化学键的断裂直接决定。θ = 36.49°和θ = 0°的纳米管均先出现了Ti6C-O3C键的断裂，其抗拉强度随温度升高表现为按指数衰减，θ = 10.47°、θ = 20.29°和θ = 90°的纳米管拉伸过程中均有Ti5C-O3C键的断裂，抗拉强度随温度升高表现为先增大后减小。

(3)相结构的不同对抗拉强度有明显的影响。随着温度的上升，手性角θ = 36.49°和θ = 0°的TiO2纳米管中FCC和BCC与HCP的占比相差不大，而手性角分别为θ = 10.47°、θ = 20.29°和θ = 90°的纳米管中HCP比例比BCC和FCC的成分多。一般来说，HCP的滑移系少，外力更容易在某个滑移方向上形成较大分力，因此抗拉强度增大，这与结论(1)中不同手性角的纳米管的抗拉强度与温度的趋势相一致。