基于差别定价的混合回收渠道闭环供应链定价和协调

王海燕，蔡圣杰

（福州大学 经济与管理学院，福建 福州 350000）

1 引言

随着电子商务的发展，市场竞争加剧，微薄的产品利润使得经营的维持更具挑战，因此除了多方面的从正向销售获取利润外，为了进一步扩大自身利润来源，或者降低规模成本，许多制造商现在并不会采用单一回收策略，开辟混合多渠道回收将成为经营决策的重要考量。因此对于多回收渠道的研究，引起了供应链领域专家学者的关注。

鉴于上述环境背景，本文的文献研究主要从再制造的闭环供应链混合回收定价以及协调契约两个部分进行。当前研究大多集中在对于单主体制造商或者零售商逆向回收方面，取得了丰硕的成果，但在混合回收渠道上的研究却有限。Min Huang，等[1]构建了一个竞争性的零售商和第三方双渠道回收CLSC模型并对决策求解，得出双回收渠道选择始终更优的结论。Hong X，等[2]讨论了三种混合回收组合方式，并且通过与单主体回收相比，MR回收模式下能取得更有益的绩效情况。Jing Zhao，等[3]研究了回收渠道的竞争和回收努力问题的混合回收CLSC。

以上文献的研究大多集中于假设消费者对于产品价格认知程度是无区别的，同时大多数文献对于契约协调的讨论也局限于特定协调契约，比较少涉及到多种契约之间的比较。因此本文试图将异质性消费者认知和混合多回收主体相结合，利用三种不同协调契约，分别对供应链模型进行优化升级。

2 问题描述与基本假设

2.1 问题描述

本文构建的混合渠道回收闭环供应链模型，是在考虑市场消费者异质性需求的基础上，制造商和零售商进行差异化的博弈定价。制造商负责新产品和再制造品的加工及回收，并将为销售给零售商的两类产品设定不同的批发价格。零售商将此作为零售价格的基础直接面向市场消费者。在回收过程中，制造商和零售商混合进入市场进行回收，零售商以一定的价格将回收的产品转移给制造商。

2.2 基本假设

假设1 假设新旧两种产品在质量、功能等方面无差异，但消费者对其两种产品价格和认知程度存在差异性。

假设2 新产品和再制品互为替代关系，为刻画两者定价和需求量关系，构造新旧产品需求函数qn=θn-pn+upr，qr=θr-pr+upn；θn＞θr，其中0＜u＜1。

假设3 假设其中的节约成本要大于回收成本，即Δ=cm-cr＞0。

假设4 两者均面对同一市场进行回收，考虑混合回收渠道的竞争性使得模型更具参考性，参考公彦德[4]的回收函数和Park S Y[5]的需求函数构造竞争性的回收函数模型，制造商回收函数为Dm=j(bm-br)，零售商回收函数为：Dr=k+hbrj(bm-br)。

假设5 供应链系统中制造商处于支配地位，零售商实力较弱，扮演追随者角色。

为了易于讨论，本文符号说明如下：w1、w2为新产品与再制品批发价；pn、pr为新产品与再制品零售价；bm和brm为制造商的直接和间接回收价；br为零售商回收转移价；cm和cr为新产品与产制品成本；θn和θr为新产品与再制品市场容量；u为两种产品价格替代系数；k为基本回收量；h为零售商回收价敏感系数；j为回收竞争价格系数；Δ为再制造中节约的成本；θ为共享契约分享比例；φ为改进型契约分享比例，为了区别两类决策和三种协调下的最优决策，集中式供应链下求解结果用上标*表示，分散式下供应链求解结果用上标**表示，共享契约、改进共享契约以及两部定价契约下的求解结果分别用上标1、2、3表示；以大M、R分别表示制造商、零售商。

3 集中决策定价模型

集中决策情形下，可以将供应链系统视为“理想化”的组织，两者不存在竞争关系，双方共同决策以价格pn、pr进行两类产品销售，以价格br进行回收，构建利润函数：

对集中式下利润函数πc求关于pn、pr、br的海瑟矩阵知存在联合凹函数，求导联立得：

4 分散决策定价模型

在分散式决策情况下，作为“理性经济人”的双方均以实现自身利润最大化为目标，在产品销售和市场回收当中进行Stackelberg主从博弈。

对于制造商和零售商的利润函数构建模型为：

对于Stackelberg主从博弈，利用逆向求解法思想。首先将式（4）对pn、pr和br求一阶导得到其反应函数为：

将式（5）带入式（3）并对w1、w2、bm和brm求一阶导并联立方程组得：

将式（6）带入式（5）得表达式（7）如下：

将上述求解所得最优解代入到各自的利润函数，可得到供应链各主体以及总的最优利润分别为由于表达式过于复杂，将在算例部分进行讨论。

5 协调定价模型

由于存在“双重边际效应”，分散式情况下系统效率不能达到最优，为了优化结果，因此本节引入收益共享契约、改进契约和两部定价契约三种契约来实现对系统改进。

5.1 收益共享契约

本节引入收益共享契约进行决策优化。在契约下，制造商压低两类产品批发价格，以此给予零售商更多市场降价空间，后期零售商将所得收益根据协商比例部分转移给对方，以此达成共赢优化的局面。假设双方协商规定以1-θ和θ的比例对收益进行分配，得各自的利润函数为：

根据Stackelberg博弈中逆向归纳法，从式（8）中求得契约条件pn、pr、br的最优解：

在契约条件下，此时分散情况下为了达到集中情况下的系统最效率，需要满足:

从而求得共享契约下的最优决策（11），表达式为：

将上述最优结果代入到各自契约下的收益函数中，得到供应链各主体以及总的利润为同时也可求出共享系数θ的取值范围，具体比例可通过双方协调决定，因为上述表达式比较复杂，将在算例分析部分进行讨论。

5.2 改进收益共享-成本共担契约

本节在收益共享契约基础上进行改进，制造商在分享收益的同时也承担部分成本费用，对分散式情况下进行帕累托改进。与收益共享契约有所区别的是双方在进行收益共享的同时，也约定好以1-φ和φ比例进行回收成本共担，因此在该契约下构建利润函数：

由于计算方法与共享契约基本相同，此处不再进行论述，可以得到改进契约下最优决策：

将上述求解所得最优解代入到各自的利润函数，可得到供应链各主体以及系统的利润分别为同时也可求出系数θ取值范围，比例大小通过双方协商决定，因为以上表达式均较为复杂，将在算例分析部分进行讨论。

5.3 两部定价契约

本节将两部定价契约引入分散式决策当中，假设双方在混合回收模式下，制造商会尽量压低两类产品批发价，从而让出一部分的收益给零售商，而在结算时对零售商收取固定费用F，由此通过签订两部定价合约实现合作关系。此时利润模型如下：

同时满足

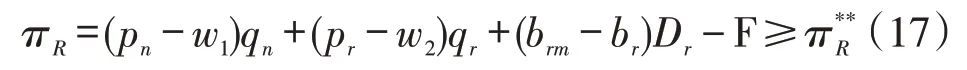
上述约束条件是指运用契约进行优化之后的零售商利润应不低于协调前的利润，这样契约才能发挥作用，协调达成一致，为了便于分析此处可假设取等计算。由于计算方法与分散决策情况类似，此处直接给出最优解：

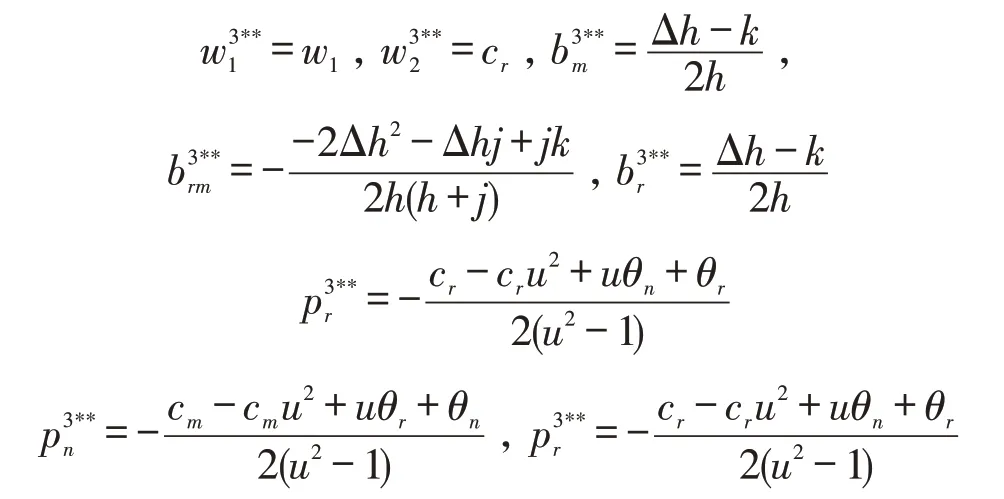
将上述求解所得最优解代入到各自契约下的利润函数，可得到供应链各主体以及总的利润分别为由于上述表达式过于复杂将在算例分析部分进行讨论。

6 算例分析

为了更清晰直观的论述和分析上述有关模型的推导，本节利用算例分析来进一步比较多主体混合回收供应链下集中和分散决策的差异性，同时也对三种协调方式的结果进行比较，以此得出最有效的系统优化方案。本文取定的参数数值如下：θn=200，θr=100，u=0.5，k=10，h=1.5，j=2，cm=30，cr=10，将以上取值代入θ表达式可以得收益分享比例范围为θ∈[0.252 872,0.5]，同理得φ∈[0.257 14,0.497]。为便于讨论，假定φ=θ=0.4。

6.1 集中与分散决策的对比

由表1可以看出最优决策方面，集中决策情况下新产品零售价pn和再制品零售价pr均低于分散情况，集中情况下的系统回收价br高于分散情况。最优收益方面，集中情况下的系统总收益大大高于分散情况。这说明，在混合回收模式下，各自追求自身收益最大化的制造商和零售商双方在制定决策时仍然存在“双重边际性”，导致系统整体的绩效受到损失，因此可以运用协调契约进行优化提升。

表1 集中与分散下的最优决策比较

6.2 三种协调下的比较

本节讨论运用三种不同的供应链协调契约对该模型进行优化提升，为了方便讨论和图表分析，以下将对三种不同契约推导讨论的顺序依次标记为契约一、二和三。其中供应链的效率表示为当前状态下的利润与集中情况下利润的一个比值，比值越高说明系统绩效与集中情况越接近，效果越优，其中供应链效率用符号λ表示。具体情况见表2。

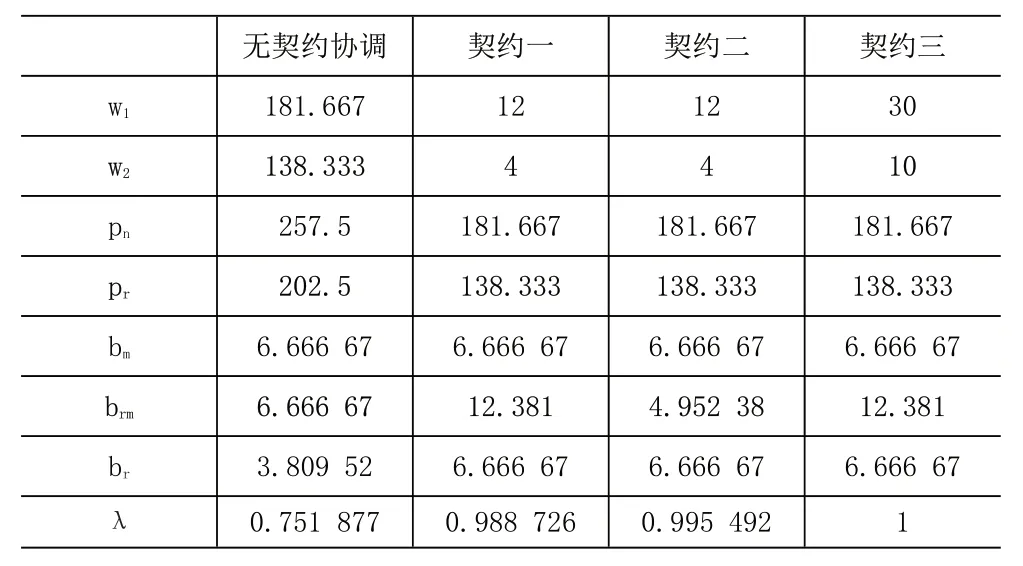
表2 四种情况下最优决策以及系统效率的比较

由表2可知三种契约调整后新旧产品的批发价格、零售价格均远低于未利用契约优化前的情况，主要是因为双方通过契约协商一致后，制造商牺牲一定的批发阶段所获取的利润给予零售商优惠，以此换取更优的结果。在价格机制作用下销售量大幅度上升，极大地优化了系统的效率。逆向回收方面，经过契约协调后的回收双方的直接回收价均大于未协调前情况，也扩大了回收量，降低了单位制造成本，改善了供应链效率。尤其是两部契约下系统效率为100%，实现了“帕累托最优”状态。

6.3 分散决策下的决策和利润关于u和j的变化

由图1可以看出，随着回收竞争价格系数逐渐增大，零售商的直接回收价也呈现缓慢上升趋势，而制造商的回收价与回收竞争价格系数无关。这说明面对相同的回收市场，随着逆向回收领域竞争程度加剧，处于追随者的零售商为了增加回收领域的市场竞争力，只能通过提高回收价格来争夺市场份额，以此保证自身的收益。进一步地，零售商回收价提高，而主导方制造商的回收决策没有改变，因此在零售商虽然收益得到一定的保障，但是与原来相比会有减少，同时伴随零售商回收价提高，回收量会扩大，因此间接减少了制造商再制造的规模成本，所以总体来看，制造商的获益大于零售商的损失，所以系统利润仍然上升。

图1 分散决策下回收价与回收竞争价格系数关系

产品替代系数的提高，说明市场消费者对于再制品的认可程度上升，环保意识加强，因此在产品选择方面，对于再制品的选择会持乐于接受的态度。因此由图2可以看出，产品替代率的提高，会导致批发转移价上升，从而带动零售价的提高。又因为再制品的热销，说明一方面产品的市场需求量较大，消费热情较高，可以通过提高新产品批发价来获得更大的利润，另一方面通过提高新产品价格来让再制品更有竞争力，从而推动再制品的热销。但是总体而言系统总利润提高。

图2 分散决策下新旧产品批发、零售价与产品替代价格系数关系

7 结论

本文构建MR混合回收的闭环供应链模型，考虑了市场消费者对产品认知度的差异，引入差别定价机制，分别求解了集中、分散两种情况下最优解和绩效，并且引入三种不同的协调契约来对原模型进行“帕累托改进”，得出以下结论：（1）混合回收情况下，供应链仍不可避免出现“双重边际性”。（2）三种协调契约中，两部定价法能够实现“帕累托最优”。（3）回收竞争价格系数仅影响零售商回收价，对于制造商利润和系统总利润有促进作用，但会减少零售商利润。（4）产品替代率对于供应链各主体的利润以及系统利润有促进作用。