基于多通道奇异谱的GNSS坐标序列粗差探测与数据插值

蔡晓军，杨建华

(长安大学 地质工程与测绘学院，陕西 西安 710054)

近20年来，随着高精度全球导航卫星观测网的发展，GPS已成为主要的大地测量技术之一，许多国家都建立了大量的GNSS连续运行观测站。这些连续的GPS时间序列有多方面的应用，例如，用于固体地球形变监测，估计GPS站点的坐标和速度等。在这些应用中，当对GPS站点的动态特性进行研究时，往往需要均匀采样的GPS时间序列，这主要是因为时间序列中间隙的存在可能会在功率谱分析结果中产生假峰，这将会影响数据分析的准确性[1]。由于各种不可预测的因素，如GPS接收器故障或观测条件不好，GPS时间序列中不可避免的存在数据缺失和粗差，另外对原始时间序列中粗差的剔除，也会造成数据的缺失，当缺失数据的分布和缺失长度存在偶然性的时候，对GPS时间序列特性分析变得非常困难。在这种情况下，鲁棒粗差探测和缺失数据插值对其具有重要意义。

目前，处理含有缺失数据的时间序列主要方法是在进行时间序列分析之前，对缺失数据进行插值。前人已经研究了多种插值方法，如临近线性插值、三次样条插值以及正交多项式插值等。选择合适的插值方法取决于缺失数据的长度和时间序列数据的特性，通常GNSS时间序列中存在不同长度缺失数据的多个数据缺口，这意味着需要研究时间序列数据缺口的特征，并选择合适的插值方法，都需要对时间序列数据缺失量的大小和类型进行初步研究[2]。因此，可能需要研究适合每个缺口的最佳内插方法，也可以针对不同长度的数据缺口应用多种内插方法来得到精确的内插结果，这就需要研究更为复杂的数据预处理程序。

奇异谱分析(Singular Spectrum Analysis，SSA)是一种强大的时间序列分析技术，Kondrashov和Ghil等首次提出并将其应用于分析不均匀采样数据，利用海面温度测量数据对模型进行测试。奇异谱分析可用于从含有噪声的采样数据时间序列重建可靠模型，而不需要任何数据的先验信息。Wang等采用SSA-M方法和SSA-IQR对GPS时间序列数据实现数据内插和粗差探测，取得较好的插值精度[2]。对于粗差探测，目前大多基于“3σ”准则进行粗差探测与剔除[3]。明锋等利用L1范数与IQR统计量组合算法探测GNSS坐标序列中的粗差，结果表明该方法是一种更具鲁棒的粗差探测方法，能够较好地探测出时间序列中的粗差，但是已存在一定程度的“误判”或“漏判”[4]。

本文采用MSSA-IQR粗差探测和MSSA缺失数据插值方法，基于传统的奇异谱分析方法，改变了求解自协方差矩阵的方法，并通过交叉验证确定模型的最佳参数。根据最佳参数建立的模型完成粗差探测及缺失数据的插值，与SSA方法不同的是，MSSA方法可以考虑多个信号之间的相关性，因此，多通道奇异谱分析获得多个信号的优质时域统计成分，最终建立既能考虑不同信号之间相关性又可降低测量噪声影响[5]。并利用模拟数据和实测GPS时间序列评估多通道奇异谱分析(MSSA)插值效果和四分位距(MSSA-IQR)粗差错探测方法，模拟数据和实测GPS数据插值结果都表明本文方法的有效性。

1 MSSA方法原理介绍

奇异谱分析是一种数据驱动的技术，通过对经验协方差矩阵进行对角化来实现，可以从含噪时间序列中提取有效信息，建立不完整数据的可靠模型，而无需事先了解时间序列的先验信息。SSA是为单变量时间序列而设计的，只能处理单个测量信号，无法考虑不同测量信号之间的相关性，但可以扩展到空间维度，即多通道奇异谱分析(MSSA)。MSSA的主要优点是能够从多变量时间序列中提取常见的季节信号、趋势项及噪声。

奇异谱分析可将时间序列分解为多个可解释的独立分量，如非线性趋势项和周期振荡分量[6]，其分析过程包括分解和重构两个步骤。MSSA作为SSA的推广，也包括分解和重构两个步骤。假设有L个时间序列且其长度为N，M为滑动滞后窗口。

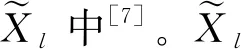
(1)

每个时间序列的轨迹矩阵的维数是R×M，其中R=N-M+1，多通道轨迹矩阵D可以定义为:

(2)

(3)

滞后协方差矩阵的维数为(L·M)×(L·M)，其中的每个元素都由式(4)计算。

(4)

奇异值分解过程，按式(5)对滞后协方差矩阵的对角化计算特征向量Ek(也称为经验正交函数EOF)和特征值λk。

Λ=ET·C·E.

(5)

式中：Λ是包含特征值λk的对角阵；E是包含特征向量Ek的矩阵。

将特征值和特征向量(λk,Ek)按照降序排列，利用得到的特征向量，计算单通道时间序列的k次主成分(RCs)，主分量表示原时间序列在特征向量上的投影[9]。

(6)

MSSA算法的最后一步是重构过程，利用之前计算的主成分和经验正交函数来计算重构(RCs)。在t通道时，第k个重构分量(RCs)由式(7)定义

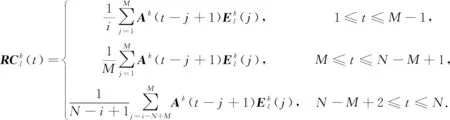
(7)

如果累加所有的RCs，将不会丢失任何信息。根据MSSA算法理论，前几个主要RCs代表趋势和振荡分量，其余RCs代表信号X中的噪声。如果选择合适数量的RCs进行重构，MSSA方法将是一种特殊类型的滤波，由于本文研究的是GPS时间序列，所以选择的RCs与年、半年周期信号相关。因此，只需要将前几个主要的RCs通过叠加来重建MSSA模型。

(8)

式中：p是主要RC的数量；l为向量个数。

2 粗差探测方法

对于GNSS时间序列的周期振荡变化，主要表现为周年或半周年的周期震荡，并以常振幅、常相位的谐波模型来描述[10]，式(9)是GPS站点运动的传统谐波模型，假设其残差序列服从正态分布，通常基于残差序列vi，采用3σ准则进行粗差探测与剔除。

y(ti)=a+bti+csin (2πPti)+dcos (2πPti)+

esin(4πPti)+fcos(4πPti)+

(9)

式(9)通常采用最小二乘估计模型参数。但是这种方法有一定的局限性：①GNSS基准站坐标时间序列中不仅含有白噪声，同时也有闪烁噪声和随机漫步噪声等有色噪声的影响，若只考虑白噪声的影响，会使估计的参数存在一定程度的偏差[11]；②传统模型假设站点的运动特性只包含线性趋势、半年度和年度振荡分量。实际上，在不同年份间，各区域气候变化存在差异，因此振荡分量的振幅可能不是恒定的。在这种情况下，式(9)可能无法精确反映GPS基准站的实际运动特征[12]；③式(9)是将各分量时间序列单独进行分析，未考虑站点3个分量之间的相关性。所以本文采用多通道奇异谱分析模型来提取GPS基准站坐标时间序列信号，该模型可以利用3个分量之间的相关性，且需要时间序列的先验信息，能够更加精确地模拟GNSS基准站的实际运动特征，从而获取较为准确的用于粗差探测的残差时间序列。

IQR粗差探测是GNSS坐标时间序列中常用的鲁棒粗差探测方法，Nikolaidis首次提出并运用该方法进行粗差探测。IQR标准探测粗差具有抵抗有色噪声的优势，使其在结合MSSA算法进行粗差识别时更具有效性。MSSA-IQR方法的具体步骤如下：首先利用交叉验证方法确定模型的最佳参数M和P，用M和P重构原始时间序列，获得残差序列，然后利用IQR准则进行粗差探测与剔除，并将剔除的数据标记为数据缺失。

2.1 交叉验证方法确定最优参数M和P

给出参数M和P的初始值，将原始时间序列y(t)中的数据分为训练数据和验证参考数据。验证数据从原始时间序列中随机抽取，在交叉验证过程中将其当作缺失数据进行插值，训练数据中缺失数据处用0填充，进行多通道奇异谱分析，计算验证部分中模型导出值与参考值(即样本值)的残差的均方根(RMSE)[13]。使得RMS最小的M和P值被认为是最优参数，并且将其用于重建MSSA模型。交叉验证方法确定最优参数M和P的算法流程如图1所示。

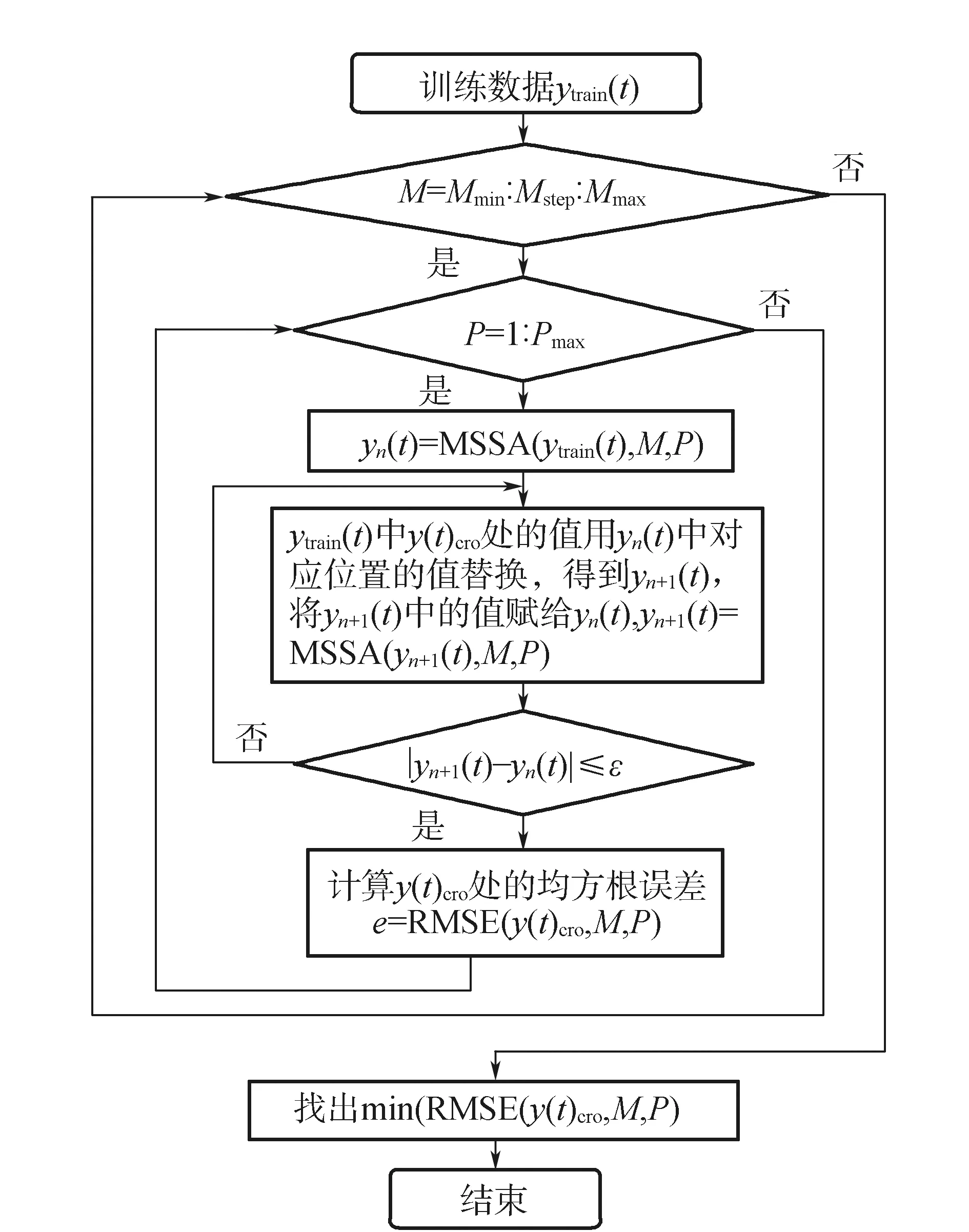
图1 确定最优参数M和P的算法流程图

M的最优值是提取模式的统计显著性和想要提取最大振荡周期之间的折衷，如果要提取GPS时间序列中存在的年度信号显然要求M大于365 d。从图1算法流程可以看出，该算法包含3层循环，如果不考虑数据的自身特性，选择从全局域搜索最佳参数，势必会影响计算效率。通常情况SSA能较好地识别出M/5-M的振荡周期[14-15]，文献[7]提出，2年或3年的滞后窗口比较适合于提取年和半年周期分量，如果需要考虑长期变化，应该采用更大的M值。在大地测量领域，采用3年滞后时间窗口从GRACE时间序列中提取长期趋势和季节变化。对于GNSS时间序列，感兴趣的是年度和半年度周期信号，2～3年大小的滞后窗口应该是比较适当的[16]。所以本文在进行模型最佳参数计算时，根据GNSS时间序列自身特点和MSSA算法的特性，以及上述文献的先验启发，适当选取迭代初值来提高计算效率。

2.2 四分位距粗差探测

将MSSA模型获取的残差序列按降序排序，该残差序列有3个四分位数，分别为上四分位数Q1、中位数Q2和下四分位数Q3。其中Q1表示在该数值之下的数据占全部数据的25%，Q2表示在该数值之下的数据占全部数据的50%，Q3表示在该数值之下的数据占全部数据的75%[11]，四分位距为

IQR=Q3-Q1.

(10)

对任一历元残差序列，分别计算四分位距和中位数，选择合适的阈值u，遍历坐标时间序列中的所有数据点，将粗差定义为：

|vi-median(v)|>u*IQR.

(11)

其中:vi是残差序列;median(v)是残差序列的中值。

当探测GNSS坐标时间序列粗差时，取u=3，根据式(11)判断原则从原始坐标时间序列中删除粗差。

3 MSSA缺失数据插值方法

MSSA迭代插值算法流程主要有以下两个步骤：

步骤一：交叉验证确定最优参数M和P。

这一步与粗差探测中最优参数M和P的确定方法类似，所不同的是将原时间序列y(t)中的数据分为训练数据、验证参考数据和待插值的缺失数据；验证数据和缺失数据处用0填补，按照图1的算法流程确定最优参数Mopt和Popt。

图2是本文计算的部分M和P的曲线图，从图中可以看出RMSE和(M，P)的关系，RMSE对重构阶数P的变化比较敏感，总体来看每条曲线都有一个极小值，图2是为了清晰的展示RMSE和(M，P)的变化规律，所以M的取值比较稀疏，实际计算过程中可选择更小的步长来寻求最佳参数。

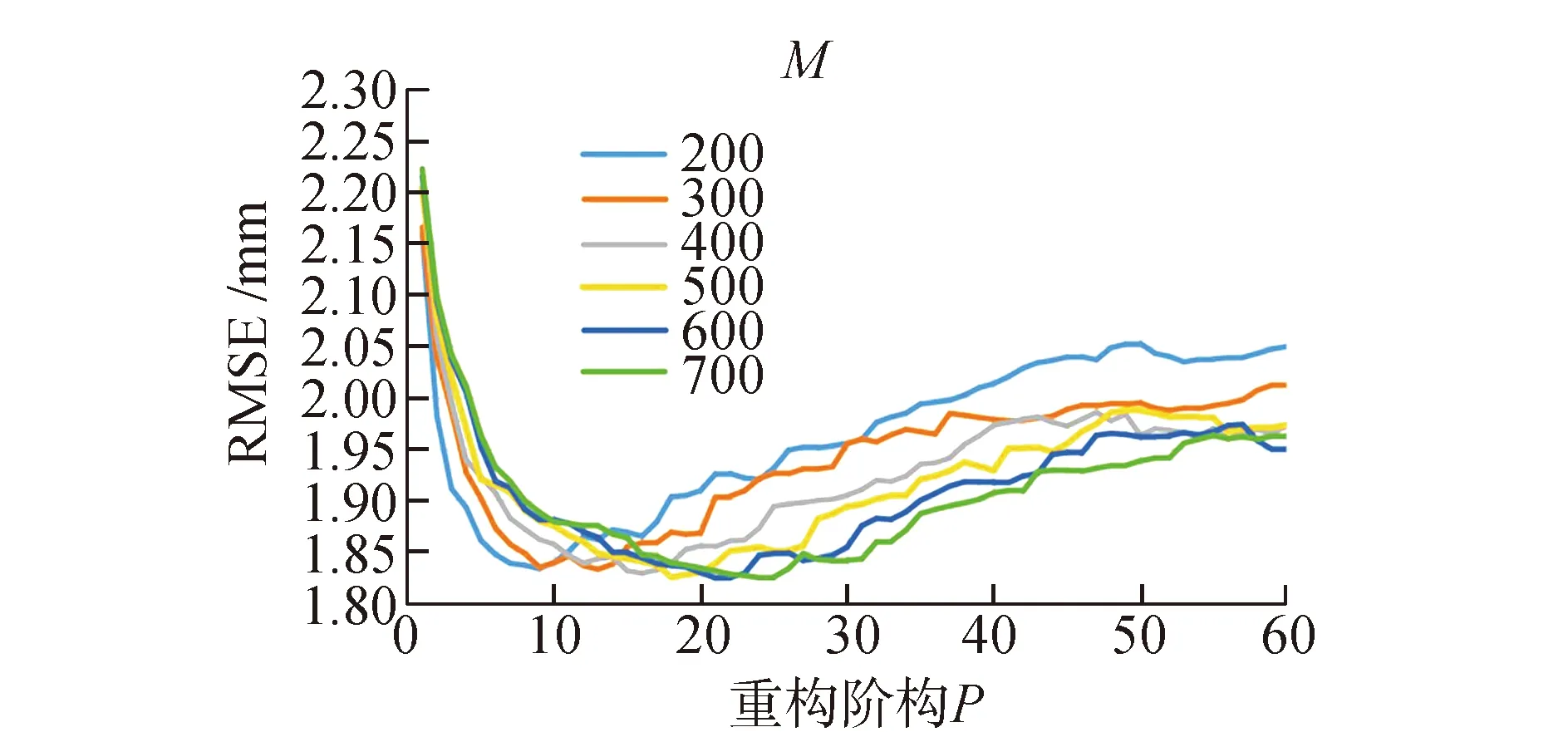
图2 LHAZ站N方向迭代结果

步骤二：MSSA插值缺失数据：

1)将剔除粗差后的原始时间序列分为训练数据和需要插值的缺失数据，缺失数据处用0填补；

2)对时间序列yn(t)进行嵌入维数为Mopt的多通道奇异谱分析，取前Popt个主要成分得到重构时间序列yrc，yn(t)中缺失数据处的值用yrc中对应位置的值替换，得到yn+1(t)；

3)计算yn+1(t)在缺失数据处的插值，重复该过程直到满足式(12)的收敛条件。

|yn+1(t)-yn(t)|≤ε.

(12)

4 模拟数据及实测GNSS时间序列分析

4.1 模拟数据分析结果

根据GNSS坐标时间序列的特点，构造包含趋势项、周期项和振幅变化因子的模拟序列，并加入有色噪声及粗差，用式(13)构造模拟数据序列。

(13)

式中：a，b，c，d，e，f分别取-1，2，1，1.2，1.2，0.8；T为200。

由式(14)向模拟时间序列数据中添加振幅变化因子信号。

u(ti)=e0.5sin(ti).

(14)

GPS时间序列的噪声通常不只含有白噪声，还有有色噪声，为了更真实的模拟GPS时间序列，生成有色噪声。

(15)

其中：w(ti)是均值为零、标准差为1的白噪声；f1和f2分别取0.2和0.2。

对模拟数据用MSSA-IQR粗差检测和MSSA插值评估算法性能。本文将生成长度为1024的模拟时间序列数据y，加入16个粗差和6段数据间隙，总共缺失170个数据，数据缺失率为16.602%。记录粗差个数和数据间隙长度及数据，图3(a)为原始含噪序列，图3(b)为加入粗差和缺失数据时段的序列。

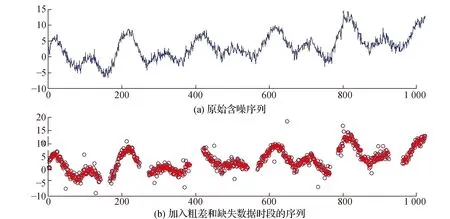
图3 含噪信号与加入粗差和缺失数据的信号

图4(a)为剔除粗差的序列，图4(b)为迭代插值的MSSA重构序列，可以看出，所有加入的粗差都被正确地探测出来，MSSA模型得出缺失样本的重构值有较高的精度。图5为重构数值残差序列，模拟噪声为零均值单位方差，MSSA模型在缺失数据序列重构的残差均值为-0.015 5，标准偏差为0.979 9。

表1中列出了模拟数据各缺失数据区间的插值结果精度，从表中可以看出，大多数缺失时段的插值均方根误差与模拟噪声的标准差接近(略好于模拟精度)，其中第1缺失时段的均方根误差最大，为1.095 1，精度稍低于其他时段，其他时间的插值点的RMSE基本接近或优于模拟数据序列中加入的标准差精度，所以在不需要任何关于时间序列的先验信息的情况下，MSSA插值也能达到较高的精度。

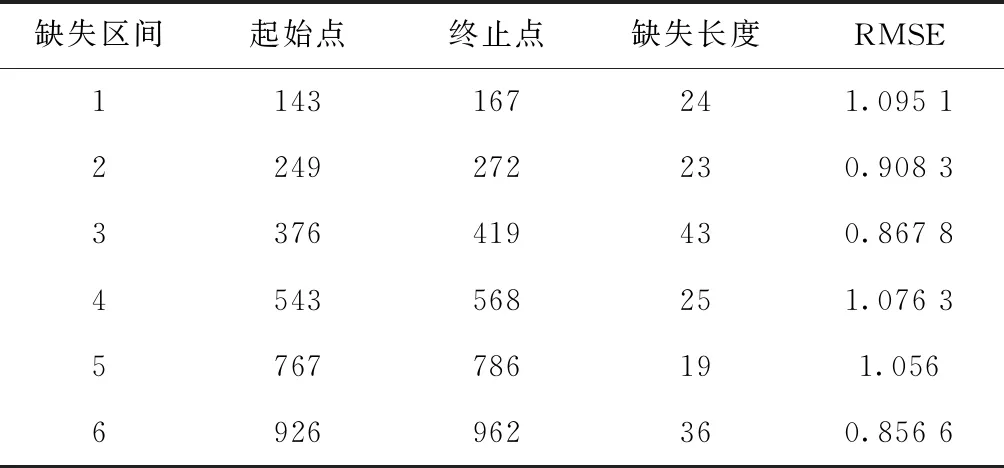
表1 精度统计

图4 粗差探测及插值结果

图5 残差序列

4.2 实测数据分析结果

本文GNSS基准站坐标时间序列数据来源于SOPAC(Scrips Orbit and Permanent Array Center, SOPAC) (http://sopac-ftp.ucsd.edu/pub/timeseries/measures/) 提供IGS站在ITRF2008框架下的单日解原始时间序列，选择中国地区的部分IGS站2001—2015年共计15年的时间序列作为实测数据进行处理，中国区域IGS站坐标时间序列概况如表2所示。

表2 中国区域IGS站坐标时间序列概况

由于各基准站的插值方法基本一致，本文选择以LHAZ站为例，进行实例数据粗差探测与插值效果分析。截取LHAZ站的时间序列数据时间跨度为2001.0014—2015.9986，总长度为5 478 d，实际观测历元数为5 137 d，缺失历元数为341 d，数据缺失率为6.223%，数据连续缺失最多为29 d。为了验证本文方法有效性，与模拟数据方法相似，在原数据序列中人为加入6个缺失数据时段，如表3所示，6个时段的缺失数据共计561个历元，LHAZ站最终时间序列总的缺失数据为902个历元，数据缺失率为16.466%，模拟缺失时段的数据如图6所示，红色数据点为缺失时段数据点。

图7为多通道奇异谱分析得到的数据插值结果与原始数据序列的比对，横轴为2001-01-01—2015-12-31的时间跨度，蓝色点是用于重建MSSA模型的样本数据点，绿色点是人为加入的缺失时段数据点，红色曲线为基于样本数据点重构的MSSA模型。现将绿色点作为验证参考点来评估MSSA模型插值结果的可靠性。图8为MSSA模型值与原始序列的残差，红色点表示缺失时段的参考值与MSSA重构插值模型的差值。

图6 实际GNSS时间序列模拟缺失时段

图7 LHAZ站MSSA粗差探测与插值结果

图8 LHAZ站残差序列

表3列出了LHAZ站各缺失时段MSSA模型插值结果和原始序列之间的均方根误差。从表中可以看出，MSSA模型结果与原始序列残差的RMSE值在水平方向除第2缺失区间的E方向为3.4 mm，其他均优于3 mm；在垂直方向上均小于7 mm。包含最大缺失数据的第3缺失区间的插值精度在水平方向优于其他时段，这表明插值精度不仅取决于缺失数据的长度，还取决于时间序列的动态特性。从LHAZ站时间序列的噪声水平和位移范围来看，上述插值精度可以被认为是好的。

为了进一步验证本文方法的可靠性，通过小波多分辨率分析迭代插值，获取缺失数据时段的插值结果。小波基选择db8小波，分解层数为6层，进行小波软阈值去噪重构原始信号，模拟数据缺失时段与MSSA方法所用数据相同，小波多分辨率分解重构在各缺失区间的插值结果的RMSE值如表3所示。从表中可以看出，两种方法除第6缺失区间的RMSE比较接近，但小波分析方法的RMSE值略大于MSSA方法，其余各方向小波分析方法的RMSE值均大于MSSA方法的RMSE值。说明MSSA模型的插值精度整体要优于小波分解重构方法，且U方向尤为明显。

表3 LHAZ站时间序列各缺失段MSSA插值精度统计

表2给出了7个台站2001—2015年共计15年的时间序列的详细统计信息，以及站点3个方向的运用MSSA-IQR方法进行粗差探测的结果，下面以拉萨站为例，对比SOPAC提供的IGS站的Clean时间序列数据与本文方法剔除粗差的时间序列的结果，如图9—图11所示，从图中可以看出，SOPAC提供的“Clean”时间序列仍然含有一定量的粗差，利用本文方法更好的剔除了原始时间序列中的粗差。

图9 LHAZ站原始时间序列

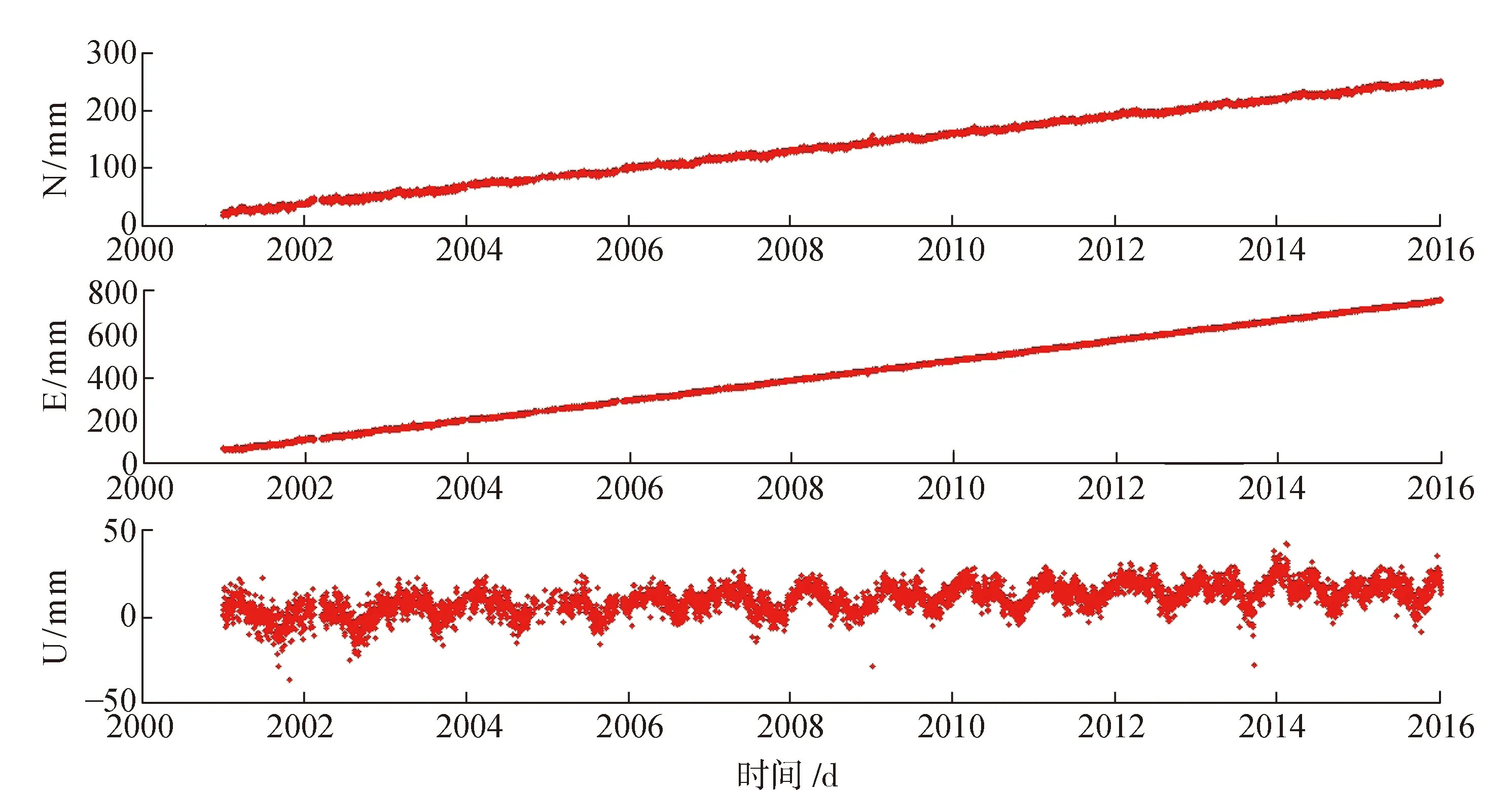
图10 LHAZ站SOPAC提供的“Clean”时间序列

图11 本文方法剔除粗差后LHAZ站时间序列

5 结 论

本文介绍了时间序列分析的MSSA理论方法，并用模拟数据和中国地区的部分IGS站2001—2015年的实际GPS单日解坐标时间序列来检验该算法在粗差检测和缺失数据插值方面的性能。模拟数据结果表明，当缺失数据也占整个时间序列的16.6%，MSSA对于缺失数据的插值也能达到较好的精度；从模拟数据结果显示MSSA-IQR能成功探测出序列中所有的粗差。实测GNSS时间序列结果表明，在不同长度的间隙和最大间隔为215个历元， 共计缺失16.466%的情况下，MSSA模型在水平方向上的插值精度大多优于3 mm，垂直方向上均小于7 mm。粗差探测方面，MSSA-IQR能够较准确的探测出序列中的粗差，可以看出，在不需要时间序列的先验信息的情况下，MSSA可以用于重构具有缺失数据的时间序列的可靠模型。