一种少自由度并联机构误差特性分析方法
曾达幸 樊明洲 张庆武 王娟娟 杨彦东 侯雨雷
燕山大学机械工程学院, 秦皇岛, 066004
0 引言
少自由度并联机构不仅具有并联机构刚度高、承载能力强和结构紧凑等特点,还具有控制方便和造价低等优点[1],广泛应用于航空、医疗等行业。作为少自由度并联机构的重要性能指标,输出精度直接影响机构的工作性能和应用场合[2]。少自由度并联机构的几何精度可以通过精度设计和运动学标定加以改善[3],而在设计阶段对少自由度并联机构进行系统的误差特性分析是消减误差、提高精度的有效途径。
许多学者对少自由度并联机构的静态误差进行了分析[4]。SUN等[5]基于闭环矢量法,将几何误差源分为补偿误差和非补偿误差两种;洪振宇等[6]根据自由度性质,将影响末端可控和不可控误差的几何误差源进行区分。而对于几何误差,常见的误差特性分析方法有D-H参数法[7]、空间矢量法[8]、环路增量法[9]等。
虽然上述方法解决了一般少自由度并联机构的误差特性分析问题,但思路均是以各项误差为整体进行误差建模,不仅建模过程较为复杂,而且无法简明快捷地分析某特定误差源对并联机构输出位姿的影响,针对性与灵活性较差。为降低少自由度并联机构的误差分析难度,提高误差分析方法的简便性与实用性,本文基于虚拟误差和并联机构影响系数原理,结合螺旋理论,提出一种无需建模即可分析少自由度并联机构误差特性的分析方法——自由度法,并进行实例分析,得到机构误差特性,同时以矢量法建立误差模型来验证所得误差特性,进而在此基础上进行样机的设计加工和试验测试。
1 基于自由度思想的误差分析
1.1 自由度与误差描述
由螺旋理论的知识可知,并联机构运动螺旋系是其所有分支运动螺旋系的交集[10]即并联机构所能实现的运动是其所有分支所能实现运动的交集,则少自由度并联机构动平台能够实现的运动自由度为可控自由度[11],否则为不可控自由度。
由于几何误差源的引入,机构的运动情况可能会发生变化,甚至机构的自由度也将改变,而几何误差源作为多维向量,并非所有维度分量都对机构输出精度有影响。基于虚拟误差原理,将各类几何误差(杆长误差、轴线误差、安装误差、运动副间隙等)拆分为X、Y、Z向位移误差与X、Y、Z向转角误差共6类虚拟误差,以单一虚拟误差源进行误差分析[12],同时根据机构的自由度性质,将6类虚拟误差分为不可控自由度误差和可控自由度误差两类进行分析;基于并联机构影响系数原理,虚设单自由度运动副作为该分支自由度性质的误差源[13],再应用螺旋理论,从自由度角度分析各分支所引入误差对机构的影响规律,形成适用于少自由度并联机构的自由度法。
如图1所示,在少自由度并联机构的分支w中,设g1为驱动副,gi(i≠1)为被动副,gi+1为虚设的单自由度运动副(以下简称运动副gi+1)。

图1 含误差源的少自由度并联机构简图Fig.1 Diagram of lower-mobility parallel mechanism with errors
保持分支w驱动副与动平台的输入输出关系不变,应用螺旋理论分析机构螺旋系及分支螺旋系,得到各分支运动自由度以及分支w中被动副gi与运动副gi+1运动螺旋系间的线性关系,得到6类虚拟误差对动平台的影响结果,进而综合出各类几何误差源对机构输出的影响情况。
1.2 不可控自由度误差的影响分析
当运动副gi+1为分支w的不可控自由度误差源时分两种情况进行分析。
(1)运动副gi+1的自由度性质为被分支w所包含且其他分支不全包含。
若等式$i+1=k2$2+k3$3+…+ki$i有解(其中$i表示该分支第i个运动副的运动螺旋),即$i+1可以被$2~$i线性表示,运动副gi+1的运动可以被本分支被动副gi的运动所补偿,则该误差不影响动平台输出精度。
若等式$i+1=k2$2+k3$3+…+ki$i无解,即$i+1无法被$2~$i线性表示,运动副gi+1的运动无法被本分支被动副gi的运动所补偿,同时受到不含该自由度分支对动平台的约束,该误差无法反映到动平台上,则该机构的装配和运动将被影响。
以3SPS/S(S为球面副、P为移动副)机构(图2)为例,该机构不可控自由度为沿X、Y、Z轴3个方向的移动。当分支1引入Z向移动副gi+1作为本分支的Z向位移误差源时,其自由度性质为被分支1所包含且其他分支不全包含(分支4未包含),且$i+1=k2$2+k3$3+…+k7$7有解,则运动副gi+1的运动可以被本分支被动副$2~$7的运动所补偿,该误差不会影响动平台的输出精度。
(2)当运动副gi+1的自由度性质为不被分支w所包含,即$i+1=k2$2+k3$3+…+ki$i无解时,运动副gi+1的运动无法被本分支被动副gi的运动所补偿。
若其他分支不全包含该自由度,则受其中不含该自由度分支对动平台的约束,该误差无法反映到动平台上,该机构的装配和运动将被影响。
若其他分支均存在该自由度,则当分支w由于所引入的误差产生该自由度运动时,其他分支无法约束,该误差反映到动平台,影响其输出精度。
同时,若误差源自由度性质为移动,则不会对动平台其他运动产生影响;若该自由度性质为转动,则会对动平台其他运动产生影响,即对该转动所伴随的两个方向的移动输出产生影响。
同样以3SPS/S机构为例,当分支4引入沿Z向的位移误差(如杆长误差)时,由于该分支自身不包含而其他3个SPS分支均包含沿Z向的移动自由度,故该位移误差只影响动平台沿Z向的位移精度。
综上,分析不可控自由度误差对机构运动影响的步骤如图3所示,可得到3种影响结果:误差被本分支补偿(不影响动平台的输出精度)、误差影响动平台的输出精度、误差使机构产生装配问题和运动问题(如机构自由度发生变化)。
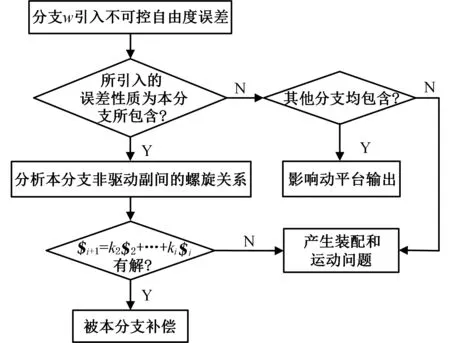
图3 不可控自由度误差的影响流程图Fig.3 Flow diagram of error of uncontrollable degree of freedom
1.3 可控自由度误差的影响分析
少自由度并联机构的耦合性使机构的某些可控自由度被多个分支控制,假设引入的运动副gi+1为分支w的可控自由度误差源。
(1)当运动副gi+1所对应的可控自由度由分支w独立控制或由分支w与其他分支共同控制时,该误差将影响动平台的输出精度。
(2)运动副gi+1所对应的可控自由度仅由其他分支控制时:若$i+1=k2$2+k3$3+…+ki$i有解,则该误差不会影响动平台的输出,而是被本分支被动副gi的运动所补偿;若$i+1=k2$2+k3$3+…+ki$i无解,则该误差会反映到动平台上,影响动平台的输出精度。
综上,分析可控自由度误差对机构运动影响的步骤如图4所示,可得到2种影响结果:误差被本分支补偿、误差影响动平台的输出精度。

图4 可控自由度误差的影响流程图Fig.4 Flow diagram of error of controllable degree of freedom
几何误差作为多维向量,它的各个维度分量对机构的输出精度影响并不完全相同,通过将其拆分虚拟误差,再由图3与图4的步骤进行分析,可清晰辨识出各几何误差的各维分量对机构输出精度的影响,对机构的加工及装配有更细致完善的指导意见。
2 机构自由度法误差分析
根据上述分析步骤,以3-CUR机构为例进行误差分析。该机构为三移动自由度并联机构[14],其可控自由度为沿X、Y、Z轴3个方向的移动,不可控自由度为绕X、Y、Z轴3个方向的转动。建立以3-CUR并联机构动平台中心为原点的机构静坐标系OXYZ,如图5所示,其中X轴与轴2平行,Y轴与轴3平行,$11为分支1驱动副的运动螺旋,$12~$15为被动副运动螺旋。

图5 3-CUR机构简图及运动螺旋Fig.5 Diagram and motion screw of the 3-CUR mechanism
2.1 3-CUR机构不可控自由度误差的影响分析
以运动副gi+1作为不可控自由度误差源。分支1的运动螺旋系为
(1)
式中,a、b、c、d、e、f、g均为任意常数。
若运动副gi+1是分支1引入的绕X轴的转角误差源,则分支1包含而分支3不包含绕X向的转动自由度,且$i+1=(1 0 0; 0hi)=k2$12+k3$13+…+k5$15有解,该误差不影响动平台输出。
同理可得,如果分支1引入绕Z轴的转角误差,该误差不影响动平台的输出。
若分支1引入绕Y轴的转角误差,由于分支1不包含而其他分支均包含绕Y向的转动自由度,且$i+1=(0 1 0;l0m)=k2$12+k3$13+…+k5$15无解,则该误差会影响动平台的输出。同时,由于该自由度性质为转动,还将影响动平台沿X轴和沿Z轴的位移精度。
2.2 3-CUR机构可控自由度误差的影响分析
当分支1引入本分支所控制的X向移动自由度误差时,该误差会影响动平台的X向位移精度。
若分支1引入沿Z轴的位移误差,显然$i+1=(1 0 0; 0 0n) =k2$12+k3$13+…+k5$15有解,则该误差不影响动平台的输出。
同理可得,如果分支1引入的为沿Y轴的位移误差,则该误差不影响动平台的输出。
综合可得,为提高3-CUR机构动平台的某向位移精度,仅需根据分析结果,有针对性地减小相应分支的某些误差源即可,其对应关系如表1所示,可避免盲目地提高机构的整体加工精度,有效降低加工成本。
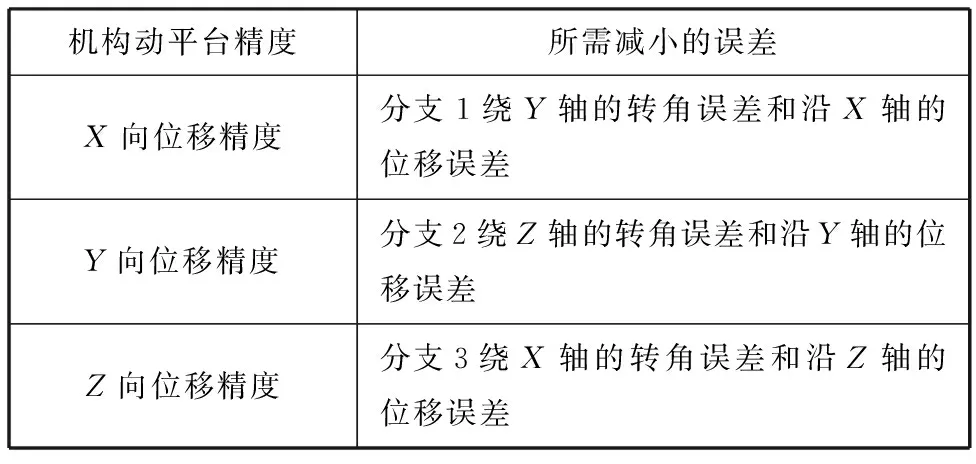
表1 分支误差与机构动平台精度的关系
由表1可知,影响机构输出精度的本质原因是6类虚拟误差,而将其组合即为各类几何误差源。以提高动平台X向位移精度为例,则只需减小分支1绕Y轴的转角误差和沿X轴的位移误差共2类虚拟误差,结合分支1存在的几何误差,如杆长误差、安装误差、轴线偏差等,则只需减小2类虚拟误差的对应项或组合项即可,即杆1的杆长误差、圆柱副绕Y向的轴线误差和圆柱副沿X向、Z向的安装误差。
3 机构矢量法误差分析及仿真
利用矢量法建立3-CUR机构的误差模型,进而分析分支误差对动平台输出的影响,并与第2节分析结果比较,以验证自由度法的正确性。
3.1 3-CUR机构误差模型的建立
如图6所示,建立3-CUR机构动坐标系oxyz和其分支1静坐标系o1x1y1z1。图中,a1为圆柱副安装位置中心点A1在坐标系{o1}中的位置,δa1为其位置偏差矢量。e1为圆柱副的理论轴线方向,其角度偏差值为δα1和δβ1,R1b为对向量e1进行修正的位姿转换矩阵,h1为圆柱副的移动距离。l11为杆1的理论长度,δl11为杆1理论和实际长度的偏差值,e2为杆1的理论方向向量,其角度偏差值为δθ1,R1c为对向量e2的修正位姿转换矩阵。杆2的理论长度为l12,δl12为其杆长误差,w1为杆2在机构静坐标系OXYZ下的方向向量,其角度偏差值为δw1。P为动平台中心点的理论位置,δP为其位置偏差矢量。d1为杆2与动平台铰接的中心点D1在分支1动坐标系下的位置,δd1为其偏差值。

图6 分支1矢量简图Fig.6 Vector diagram of branch 1
建立分支1的矢量闭环方程:
R1a1+h1R1R1be1+l11R1R1bR1ce2+l12w1=
R1P+R1R1Od1
(2)
式中,R1为分支1静坐标系相对于机构静坐标系的转换矩阵;R1O为分支1动坐标系相对于分支1静坐标系的转换矩阵。
假设所有误差源均为微小变量,对式(2)进行微分运算可得
δa1+h1δR1be1+δl11R1bR1ce2+l11δR1bR1ce2+
l11R1bδR1ce2+δl12w1+l12δw1=δP+R1Oδd1
(3)
令δu1=[δα1δβ10]T,δv1=[0 0 δθ1]T,有δR1b=δu1×R1b,δR1c=δv1×R1c,消去δw1得
令
F1=[δa1δu1δl11δv1δl12δd1]T
可得
(4)
同理可得分支2和分支3的矢量闭环方程:
(5)
(6)
式(4)~式(6)联立得
δP=J·δp
(7)
式(7)即为3-CUR并联机构的误差映射模型。
3.2 3-CUR机构误差影响分析仿真
首先设定仿真所需的机构参数,取3-CUR并联机构水平最大运动直径为120 mm,设定机构杆1长度l11=80 mm,杆2长度l12=188 mm,杆2与动平台铰接的中心点距离动平台中心d1=45 mm,3个圆柱副各轴线间的距离为216 mm。同时,在3-CUR并联机构的工作空间内,选取一个不失一般性的工作平面作为机构MATLAB仿真运动的工作空间,所选工作空间为
(8)
式中,γ1、γ2、γ3分别为分支1、分支2、分支3驱动副的驱动角度。
3.2.1 机构不可控自由度误差源的仿真分析
在给定工作空间内,当分支1引入圆柱副轴线角度误差时,即X向转角误差δα1=0.1°、Y向转角误差δβ1=0.1°,尽管动平台绕X、Z方向的转角误差和沿Y向的位移误差为零,但该轴线误差使动平台产生了绕Y轴的转角误差,同时还产生了沿X轴和Z轴方向的位移误差,见图7~图9。
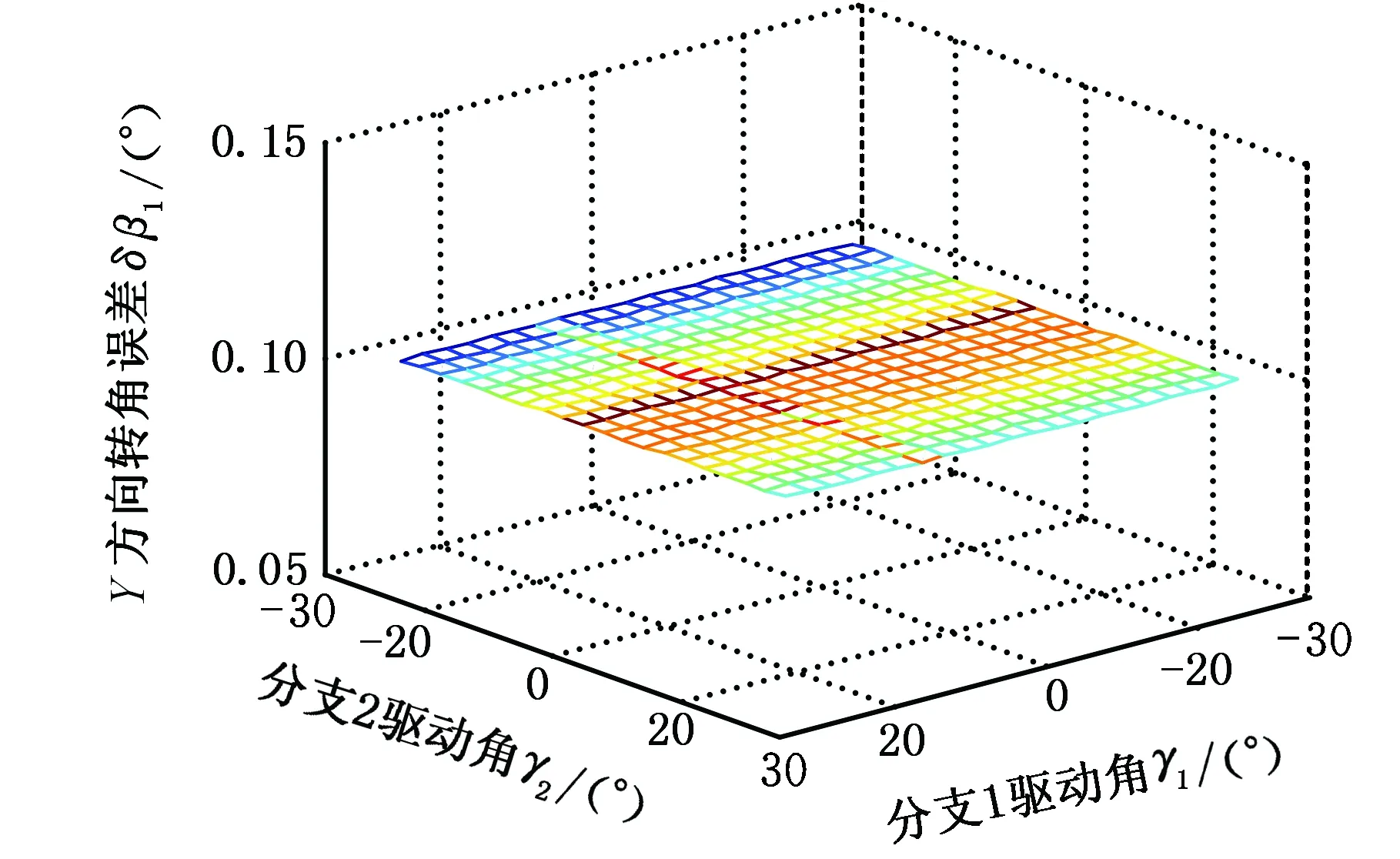
图7 轴线偏差对动平台Y向转角精度的影响Fig.7 Rotation accuracy of the moving platform along Y-direction under different axis-offset
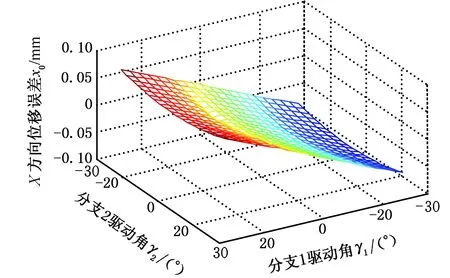
图8 轴线偏差对动平台X向位移精度的影响Fig.8 Displacement accuracy of the moving platform along X-direction under different axis-offset
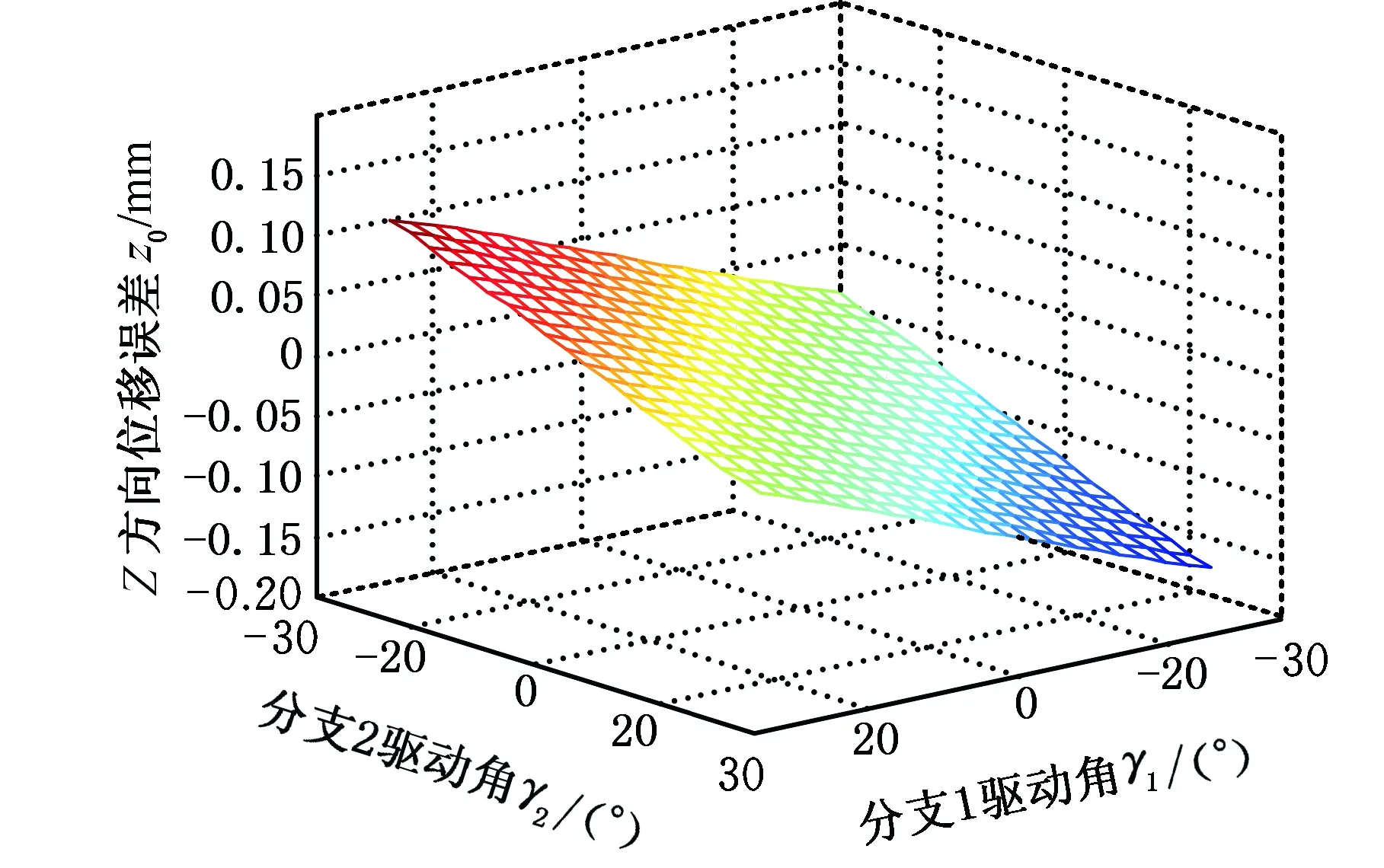
图9 轴线偏差对动平台Z向位移精度的影响Fig.9 Displacement accuracy of the moving platform along Z-direction under different axis-offset
在图8、图9中,动平台产生了沿X轴和Z轴方向的位移误差。这是由于当动平台绕某一坐标轴转动时,另外两个坐标轴产生随动,即动平台产生绕Y轴的转角误差时,会使动平台产生沿X轴和Z轴方向的随动误差,即图7所示的Y向转角误差引起图8所示的X向位移误差与图9所示的Z向位移误差。
而当使Y向转角误差δβ1=0°时,经仿真发现,动平台各向输出误差均为零,说明是分支1中Y向转角误差影响了动平台输出精度。
当分支1引入圆柱副驱动误差时,即Z向转角误差δθ1=0.1°,由仿真分析可得,动平台各向输出误差均为零。
以上仿真结果与2.1节得到的结论相同。
3.2.2 机构可控自由度误差源的仿真分析
假定分支1引入的圆柱副安装位置误差为δa1=[0.2 0.2 0.2]T,分别对机构动平台各自由度产生的误差进行仿真分析,得到动平台绕X、Y、Z轴3个方向转角和沿X、Y、Z轴3个方向位移误差变化情况。
由图10可知,在给定工作空间内,该圆柱副安装误差影响动平台X向的位移精度。通过仿真发现,该误差并不影响动平台其他5个自由度的运动精度。
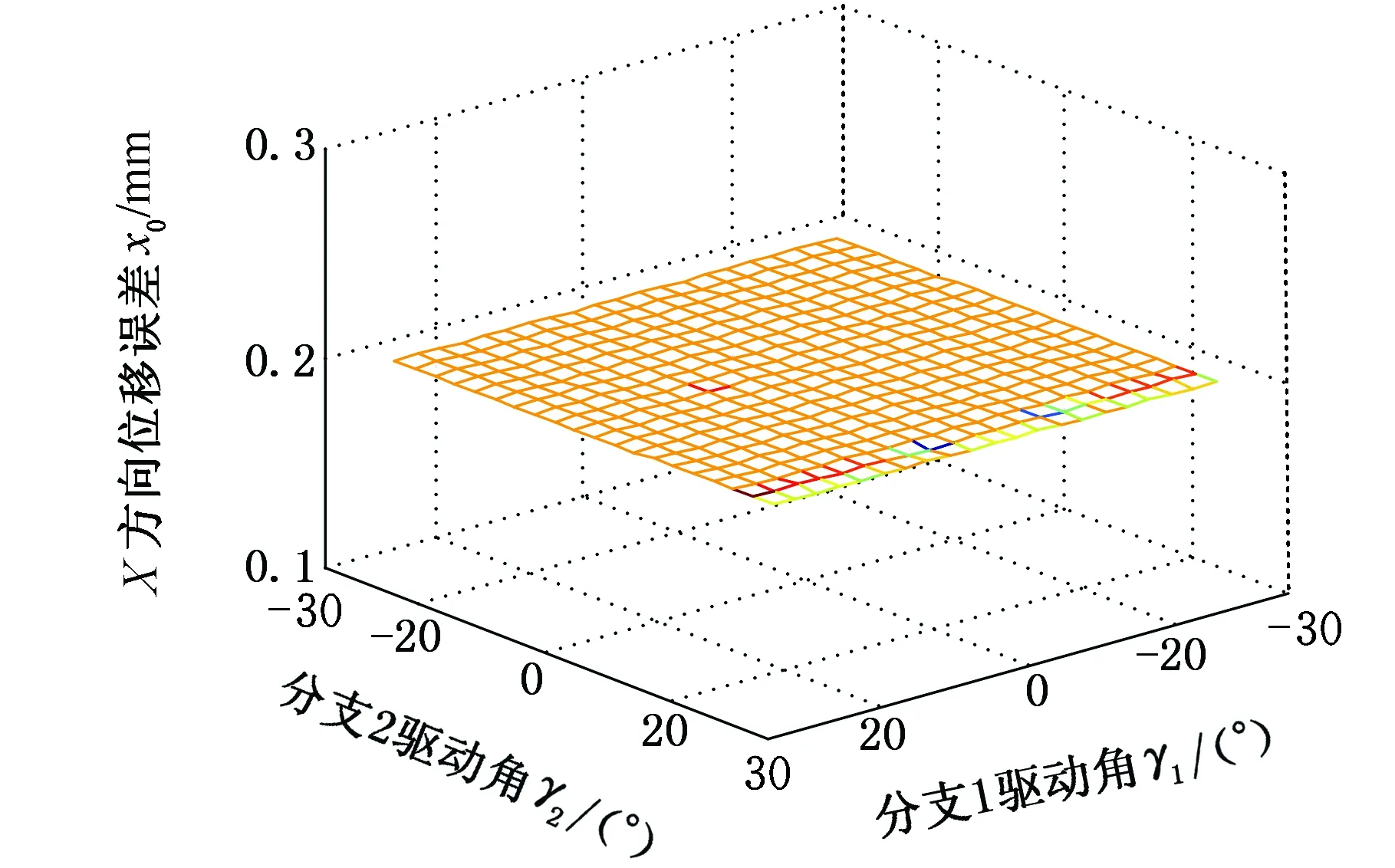
图10 安装误差对动平台X向位移精度的影响Fig.10 Displacement accuracy of the moving platform along X-direction under different installation error
当引入的安装位置误差为δa2=[0.2 0.2 0.2]T时,仿真分析发现,动平台各向输出误差均为零,说明在分支1的3个位移误差中,仅X向的位移误差影响了动平台的X向位移精度。
圆柱副的安装位置误差为X、Y、Z轴3个方向的位移误差,而杆件的杆长误差同样是沿此3个方向的位移误差,仿真分析结果相似,在此不予赘述。
以上仿真结果与2.2节得到的结论相同。
综上所述,经过误差建模和仿真分析得到的分析结果与第2节通过自由度法分析得到的误差规律一致,验证了自由度法的正确性。
4 样机制作与试验
3-CUR机构为机械本体,根据第3节中的机构尺寸设计制作3D打印机样机。由于3D打印机是按规划路径进行逐层打印,平面运动是其最主要运动形式,同时为避免层与层之间黏结性等因素对机构误差特性检验结果的干扰,选择打印圆筒试件,检测其OXY平面的轮廓线误差,验证3-CUR并联机构的误差特性。
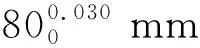
所制作的样机和控制柜如图11所示。

图11 3-CUR并联式3D打印机Fig.11 3D parallel printer of 3-CUR
所打印圆筒试件外轮廓半径理论值为24 mm,在试件外轮廓取X向、Y向轮廓线测量点各5个,如图12所示。测量方法参照文献[15]轴承套圈沟心距检测技术,通过Marsurf XC 20轮廓仪在测量点处沿圆筒试件外轮廓划一段弧线,得到实际轮廓线,进而拟合获得测量点外径测量值,如图13所示。

图12 圆筒试件检测点图Fig.12 Detection point map of the cylinder specimen

图13 检测试验及轮廓拟合图Fig.13 Detection testing and contour fitting
试件X向、Y向轮廓线点外径测量值及相对误差分别如表2、表3所示。
由表2、表3可知,该圆筒外径轮廓线实际测量值与理论值沿X向的相对误差平均值为0.52%,Y向的相对误差平均值为1.01%,可见样机的X向位移精度高于Y向位移精度,与预期结论相同,再次验证了自由度法的正确性。

表2 X向轮廓点测量值及相对误差

表3 Y向轮廓点测量值及相对误差
5 结论
(1)提出了一种无需进行误差建模的误差特性分析新方法——自由度法。该方法将机构误差分为可控自由度误差和不可控自由度误差,通过虚设运动副,应用螺旋理论可灵活分析某特定误差各维分量对机构输出精度的影响,可用以指导机构的具体加工和装配。
(2)根据所提出的自由度法得到3-CUR并联机构的误差特性,矢量法分析和样机试验均验证了所得误差特性的正确性,证明了所提方法可准确且详尽地分析机构误差特性并提高机构的输出精度,对并联机构的精度研究和成本控制具有借鉴意义。

