应用扰动广义微分求积法的复合材料层合板剪切屈曲分析与优化

孙士平 张 冰 胡 政

南昌航空大学航空制造工程学院，南昌，330063

0 引言

航空结构中复合材料层合板作为组成薄壁结构的板壳类构件承受着复杂载荷工况，其抗屈曲稳定性能倍受重视，精确预测其屈曲性能成为高品质结构设计的必要前提。研究者采用各种数值方法开展了复合材料层合板的屈曲性能分析，对轴压载荷屈曲问题进行了深入研究，取得了显著成果，但对剪切屈曲问题研究不多[1-6]。近期有TARJAN等[7]采用Ritz法计算了均布、线性变化轴压及剪切载荷作用下正交各向异性复合材料层合长板的屈曲性能；YANG等[8]结合配点法推导出四边固支正交各向异性方板剪切屈曲问题的一般解析解，简化了计算过程；SELYUGIN等[9]基于有限元法分析了单/双轴剪切载荷工况正交各向异性长板的剪切屈曲性能及弯扭耦合对剪切屈曲性能的影响；JUNG等[10]提出改进8-ANS壳单元研究了剪切载荷和铺层顺序对复合材料层合壳屈曲行为的影响；刘庆辉等[11-12]和CHEN等[13]则分别采用Ritz法、Galerkin法分析了剪切、剪切与面内线性变化载荷组合工况下，带扭转约束正交各向异性长板的屈曲问题，计算结果与有限元数值解相吻合。这些剪切屈曲研究主要以正交各向异性板为对象，研究层合板尺寸、弯扭耦合对剪切屈曲性能的影响规律，较少关注各向异性对称复合材料层合板的剪切屈曲分析及铺层顺序优化。

不同数值方法求解复合材料层合板屈曲问题的计算效率存在较大差异，应用智能搜索算法开展复合材料层合板屈曲优化特别是含耦合项而无封闭解的各向异性复合材料层合板屈曲优化，需要耗费大量的屈曲响应分析次数，高效的数值方法会显著减少优化时间。广义微分求积法[14](generalized differential quadrature,GDQ)是从微分求积法[15](DQ)发展而来的一种更稳定高效的数值方法，已应用于许多力学问题求解。KADKHODAYAN等[16]采用GDQ法分析了均质矩形板的弹/塑性屈曲问题；李威等[17]采用GDQ法分析了受切向力作用的梁的稳定性问题；DARVIZEH等[18]通过均布轴压作用复合材料层合板屈曲问题的计算比较证明，GDQ法能比Ritz法更高效精确地求解复合材料层合板屈曲问题；MAAREFDOUST等[19]采用GDQ法分析了中厚斜型均质板的剪切屈曲问题。采用GDQ法开展各向异性复合材料层合板的剪切屈曲分析与优化研究尚未见报道。

本文采用GDQ法开展对称复合材料层合板的剪切屈曲分析与铺层优化。针对GDQ法求解层合板屈曲问题存在计算精度差、不稳定收敛现象，提出权重系数扰动策略来改进GDQ法的计算收敛性，实现扰动GDQ法对层合板剪切屈曲的稳定有效计算。在此基础上，结合直接搜索模拟退火算法[20]开展复合材料层合板的铺层顺序优化，比较边界条件、长宽比、铺层数和铺层形式对剪切屈曲性能的影响，研究轴压与剪切载荷组合工况下，不同长宽比和载荷比时层合板屈曲性能的变化规律。

1 复合材料层合板描述

1.1 基本方程

(a)层合板载荷边界 (b)层合板铺层结构图1 对称层合板示意图Fig.1 A schematic of symmetrical composite laminate

承受剪切和均匀轴压载荷作用的对称复合材料层合板如图1所示，长a、宽b、厚h，总铺层数为2L。层合板第l层铺层的纤维角度为θl，第l层铺层下表面到中面的距离为zl。

基于经典层板理论的对称复合材料层合板屈曲微分方程为

(1)

其中，w即w(x,y,t)为中面位移函数；t为时间；Nx和Ny分别为层合板在x和y方向承受的轴向载荷;Nxy为层合板在xy平面内承受的剪切载荷；Dij(i,j=1, 2, 6)为层合板刚度矩阵元素, 其计算公式为

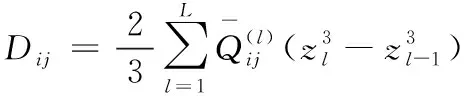
(2)

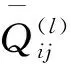
层合板的边界条件常用S(simply supported，简支)、C(clamped，固支)以及F(free，自由)4位字母组合表示，如边界条件SCSC中第1和第3位字母S分别表示x=0和x=1边为简支边界，第2和第4位字母C分别表示y=0和y=1边为固支边界。以层合板x=0边为例，固支边界为

(3)

简支边界为

(4)

1.2 控制方程的GDQ求解

GDQ法是一种求解常(偏)微分方程的数值计算方法。若一维函数f(x)在区间[0, 1]上连续可微，则其n阶导数可用定义域内任意N点的函数值线性加权组合表达：

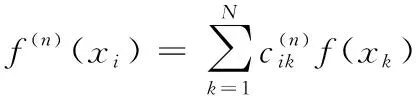
(5)

i=1,2,…,Nn=1,2,…,N-1

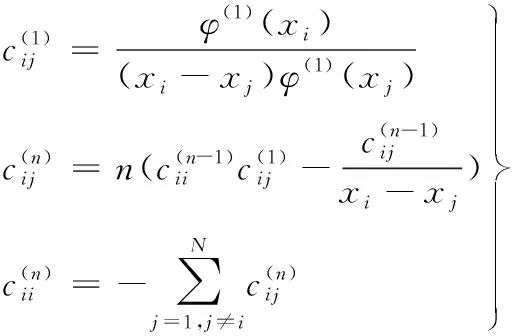
(6)

i,j=1,2,…,Ni≠jn=1,2,…,N-1

对于二维函数g(x,y)，其导数可按下式计算：

(7)

i=1,2,…,Nj=1,2,…,Ms,q≥0

s+q=1,2,…,N+M-2

令层合板长宽比λ=a/b，取位移函数w(x,y,t)=W(x,y)eiωt，并设X=x/a、Y=y/b，将式(1)变换处理为

(8)

将式(7)代入式(8)得

(9)

将式(7)代入式(3)和式(4)并进行归一化处理，得到以X=0边为例的边界表达式，固支边界：

(10)

简支边界：

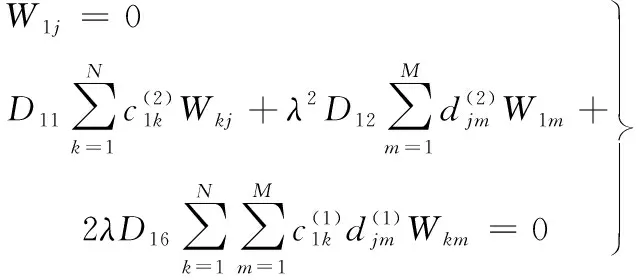
(11)

记格栅点位移向量W=(Wb,Wd)T，其中下标b表示边界上及与其相邻的(4N+4M-16)个格栅点，下标d表示余下的(N-4)×(M-4)个内部格栅点。利用式(10)、式(11)分别置换式(9)的第1、2、N×(M-1)、N×M方程实现边界条件的施加，得到矩阵表达形式：

(12)

消除变量Wb，式(12)整理可得特征方程：

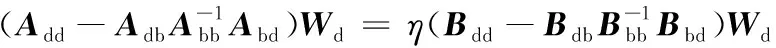
(13)

其中，Add和Bdd为(N-4)×(M-4)阶方阵；Abb为4N+4(M-4) 阶方阵；Adb和Abd分别为(N×M-4N-4M+16)×(4N+4M-16)和(4N+4M-16)×(N×M-4N-4M+16)阶矩阵；η为屈曲载荷系数。求解特征方程(式(13))可得到最小特征值所对应的临界屈曲载荷系数ηcr，将其归一化处理为量纲一临界屈曲载荷系数k*：

(14)

D0=E2h3/[12(1-ν12ν21)]

式中，E2为铺层在方向2的弹性模量；ν为泊松比。

2 扰动GDQ法

基于MATLAB平台编程实现GDQ方法的计算，离散格栅点按以下Chebyshew多项式确定位置：

(15)

栅格点划分如图2所示，其特点是临近边界处的栅格点较密，而远离边界处的栅格点少，既有利于边界条件的实施，也能保证在栅格点较少的情况下得到较精确的计算结果。

2.1 GDQ法的收敛性改进

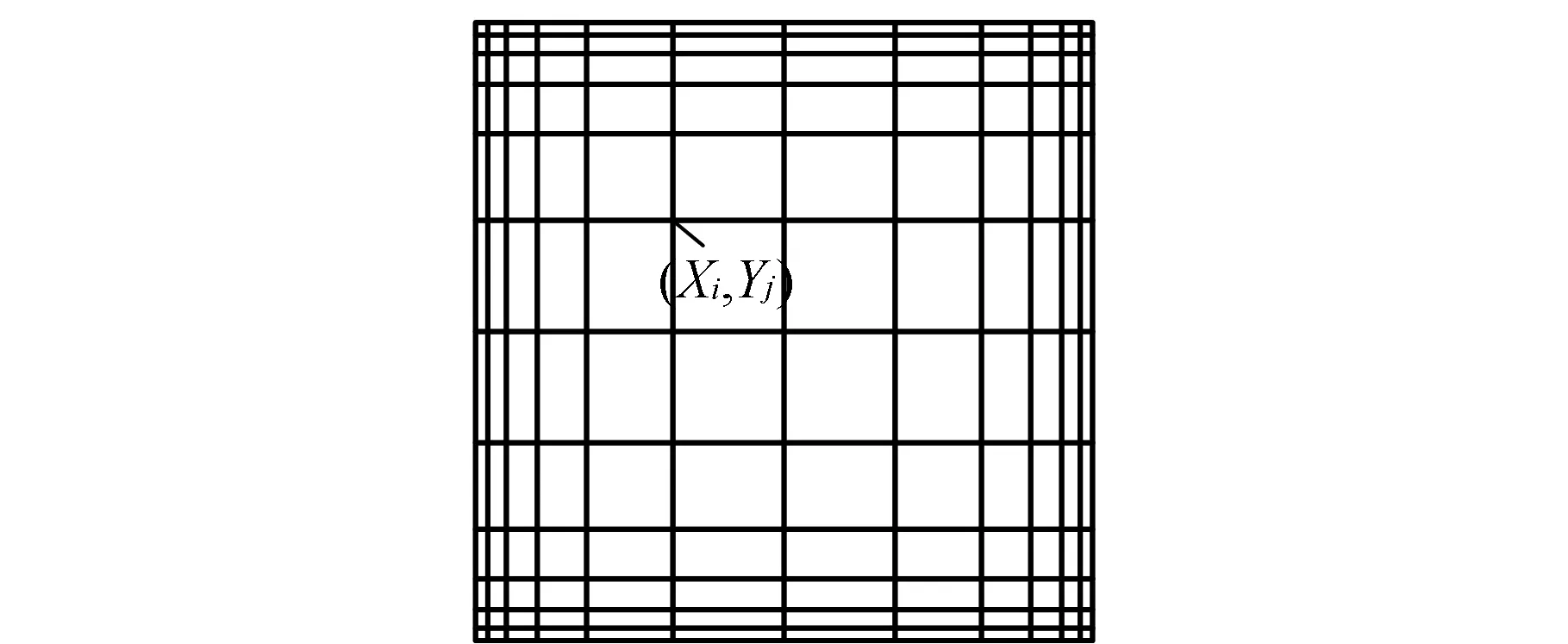
图2 归一化设计域栅格点划分示意图Fig.2 Normalized design domain grid point division diagram

表1 复合材料性能参数

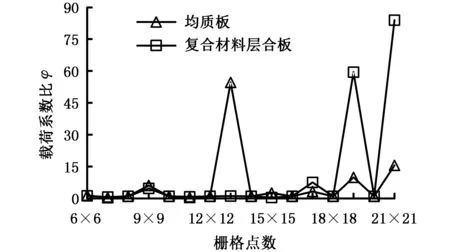
图3 基于GDQ法的矩形板φ曲线Fig.3 Rectangular plate φ curve based on GDQ method

由图3可知，随着栅格点数的增加，无论复合材料层合板还是均质板，GDQ法计算获得的剪切屈曲对比指标φ均未稳定趋于1，都存在较大波动。φ的波动反映了GDQ法求解剪切屈曲问题存在精度差、计算振荡不收敛问题。要利用GDQ法进行剪切屈曲问题求解就必需采取有效措施改进GDQ法的计算稳定性和精度。

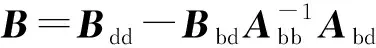
为此，提出权重系数扰动策略，对GDQ的n阶导数权重系数矩阵的主对角线元素进行扰动：

(16)

采用扰动策略的矩形板屈曲性能计算结果如图4所示，可以看到随着栅格点数的增加，无论复合材料层合板还是均质板，扰动后的GDQ法(简称扰动GDQ法)计算获得的φ稳定趋于1，与图3相比，仅用较少的栅格点数(如10×10)就能获得稳定收敛的计算结果，说明扰动GDQ法求解层合板屈曲问题的计算效率和稳定性相比于GDQ法得到了有效改进。

图4 基于扰动GDQ法的矩形板φ曲线Fig.4 Rectangular plate φ curve based on perturbed GDQ method

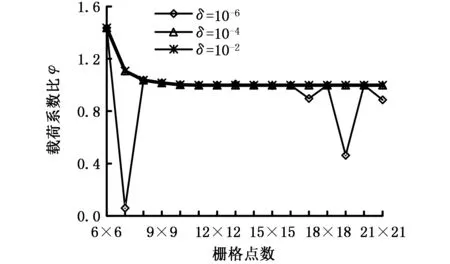
图5 扰动量δ对计算收敛的影响(λ=2)Fig.5 Influence of disturbance δ on computational convergence(λ=2)

2.2 扰动GDQ法的计算验证

采用扰动GDQ法分别计算均质板和复合材料层合板的屈曲性能来验证计算结果的可靠性，计算中栅格点数取15×15。

考虑SSSS和CCCC边界，不同λ时承受剪切力Nxy=-1N作用的均质矩形板临界屈曲载荷系数k*计算结果如表2所示。材料弹性模量E=200 GPa，泊松比ν=0.3。可以看出，扰动GDQ法计算结果与文献[21]Ritz法的计算结果基本一致。

考虑剪切与均布轴压载荷组合作用，λ=2时SSSS边界斜交铺设复合材料层合板[(±θ)2]s的临界屈曲载荷系数k*受铺层角θ变化的影响。剪切力Nxy=-1N，组合工况1为Nx∶Ny∶Nxy=1∶0∶1；组合工况2为Nx∶Ny∶Nxy=1∶1∶1。铺层材料性能如表1所示，分别采用扰动GDQ法和FEM进行计算获得的结果如图6所示。由图6可知，不同组合工况下扰动GDQ法计算结果与FEM结果的最大相对差异仅1.29%，吻合度较好。另外，给定θ时工况1的k*要明显大于工况2的k*，虽然两种工况均在θ=0°时取得最小k*，但分别在50°和70°附近获得最大k*且k*值差异高达2.3倍；两种工况下通过变化θ均能有效提高k*，相对于对应工况的最小k*，提高幅度高达300%和500%，说明铺层角度优化能显著提高复合材料层合板的抗剪切屈曲能力。

表2 均质矩形板k*的计算结果对比

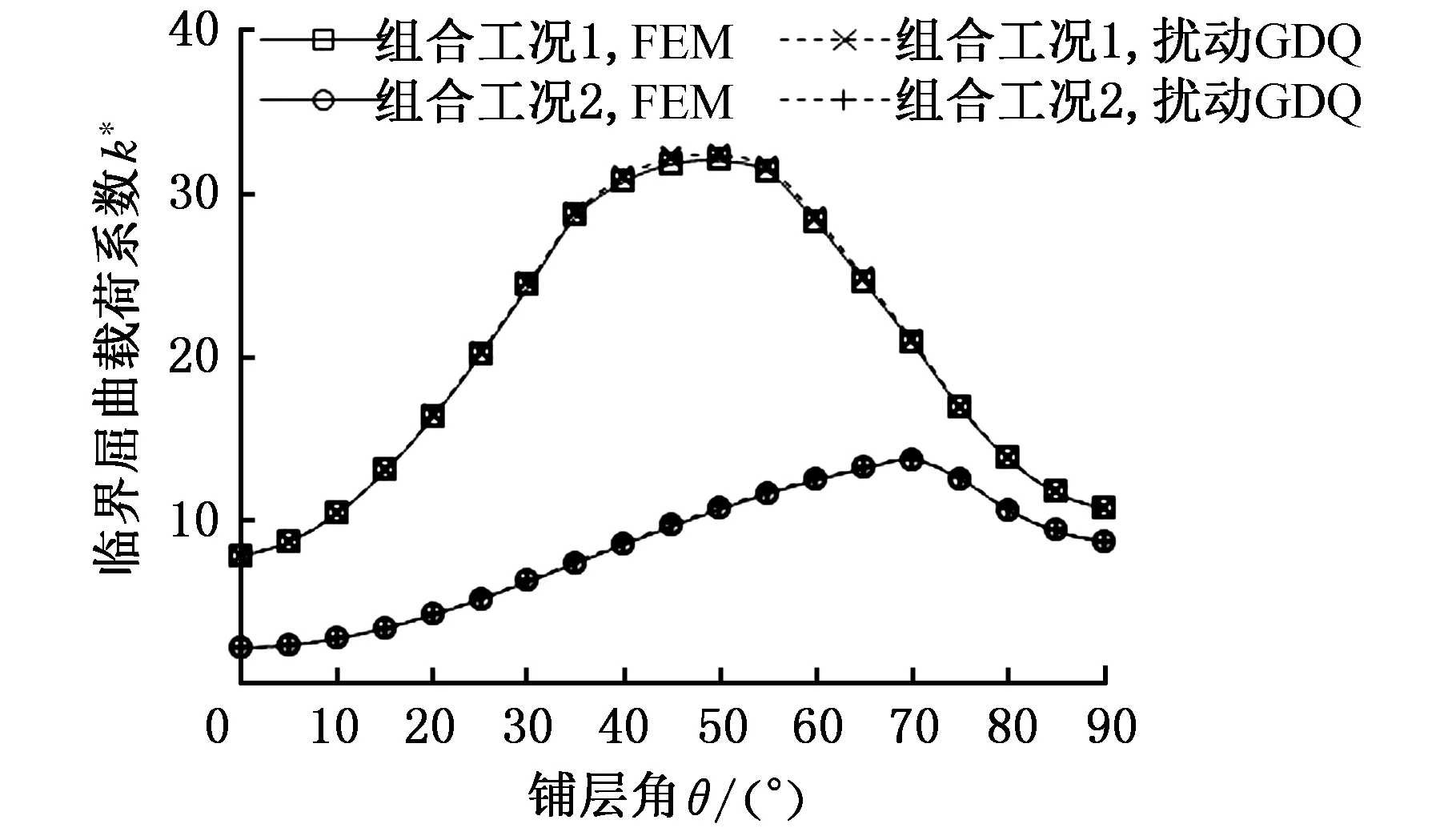
图6 复合材料层合板k*不同方法计算结果比较Fig.6 Comparison of calculation results of composite laminate k* using different methods

考虑单位长度正剪切Nxy=1N、负剪切Nxy=-1N载荷作用工况，λ=2的复合材料层合板[(±θ)2]s在CCCC、SSSS、CSCS、SCSC 4种边界时，k*随θ变化曲线如图7所示。

图7a显示，负剪切工况时k*随θ的变化为单调凸变化，不同边界下k*均在θ=0°最小而在接近60°区域最大；而图7b中，正剪切工况下k*随θ的变化为非凸变化，不同边界下k*均在θ=5°附近最小而在接近55°区域最大，此时θ变化对k*值的影响小于负剪切工况时的影响；另外，图7中两种剪切载荷下，SCSC和CSCS边界的k*值均位于CCCC和SSSS的k*值之间，且在θ从0°趋于90°的过程中，SCSC的k*逼近CCCC的k*，而CSCS的k*逼近SSSS的k*。由此可见，铺层角θ对剪切屈曲性能影响明显，边界条件变化不会改变铺层角对剪切屈曲的影响规律，但正剪切载荷会使层合板屈曲性能的铺层顺序优化求解复杂化。

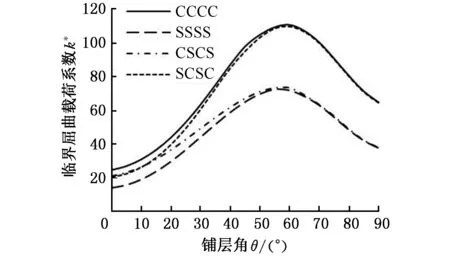
(a)Nxy=-1N

(b)Nxy=1N图7 λ=2时不同边界下铺层角θ对k*的影响Fig.7 Influence of lay angle θ on k* at different boundary when λ=2

通过上述算例的计算数据比较分析，说明采用扰动策略的扰动GDQ法能有效进行矩形板的剪切屈曲问题分析，获得的计算结果准确可靠。

3 复合材料层合板的屈曲优化

总层数为2L的对称复合材料层合板[θ1/θ2/…/θL-1/θL]s，铺层材料参数如表1所示，板长a=500 mm，t0=0.125 mm。以铺层角θl(l=1, 2,…,L)为设计变量，最大化层合板k*的优化模型：

(17)

式(17)为多极值离散优化问题，本文采用自适应直接搜索模拟退火算法求解，离散变量θl的增量取Δθ=1°，每个问题进行40次优化统计计算结果。

3.1 剪切载荷工况

基于式(17)进行单位长度剪切力Nxy=-1N作用复合材料层合板[(±θ)2]s的优化，获得λ为0.5～3时，SSSS、SCSC、CCCC 3种边界下的优化结果，如图8所示。图8显示，随着λ的增大，3种边界下k*均呈单调递减，且降速随λ增大而逐渐减小；其中SCSC边界下k*随λ增大，从接近SSSS的k*而逐渐趋于接近CCCC的k*，说明对于复合材料层合长板，长边的边界约束显著影响屈曲性能，而短边的边界约束对屈曲性能影响较小，可以忽略。同时，当λ从0.5增大到3，3种边界对应最优角度从略大于30°逐渐趋于60°，除SSSS为单调递增外，SCSC在λ<1时最优角度增大较快，在λ=1达到54°后随λ增大而平缓增长。另外，因边界条件和结构的对称性，SSSS和CCCC边界下λ与1/λ的层合板最优铺层角互为补角。

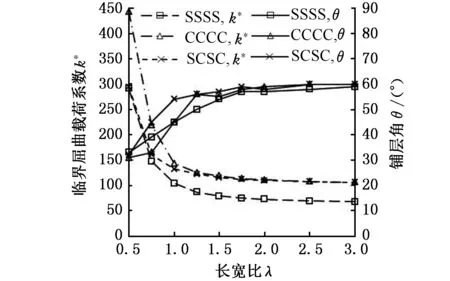
图8 3种边界下的优化结果比较Fig.8 Comparison of optimization results for 3 boundaries

考虑任意铺设对称复合材料层合板[θ1/θ2/θ3/θ4]s在SSSS、SCSC、CCCC边界和不同λ时的优化结果如表3所示。表3数据显示，不同λ时，3种边界的优化铺层均具有相同或相近的角度值，并随λ从0.25增大到3，最优铺层角从近30°递增趋于60°，而k*先快速下降后趋于平缓减小，与图8的规律相同；另外，表3中SSSS边界优化铺层顺序与文献[22]优化结果基本相同，差异在于文献[22]取增量Δθ=0.1°而更精确。进一步优化λ=2时，SSSS边界铺层顺序为[θ1/θ2/…/θL-1/θL]s的2L层对称复合材料层合板，获得最优铺层顺序近似为[(57)L]s，对应k*=93.20。以上结果说明，剪切载荷作用的对称复合材料层合板铺层顺序优化中，铺设形式与铺层数的影响较小，可简化为单变量优化问题来提高优化效率；层合板长宽比对剪切屈曲的影响随长宽比增大而减小，当长宽比大于2后，优化铺层角接近60°。计算结论与复合材料结构设计手册[23]的相关论述一致，说明扰动GDQ法求解剪切屈曲是有效可行的。

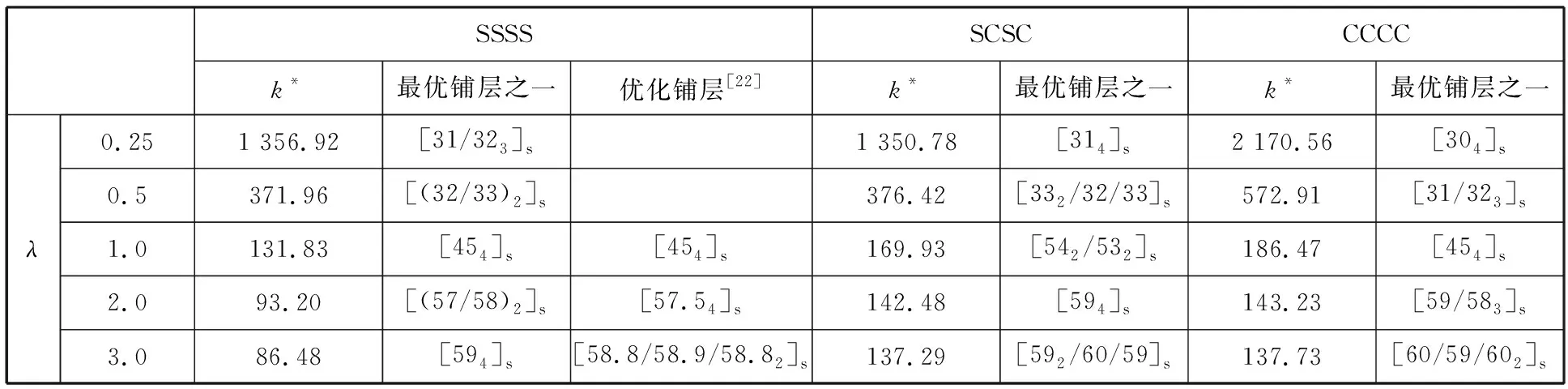
表3 剪切载荷作用对称复合材料层合板屈曲优化结果

3.2 剪切与轴压载荷组合工况

考虑复合材料层合板[θ1/θ2/θ3/θ4]s承受剪切与轴压载荷组合工况，分X向轴压组合工况(Nx∶Ny∶Nxy=1∶0∶1)和双轴压组合工况(Nx∶Ny∶Nxy=1∶1∶1)，其中Nxy=-1N。在SSSS、SCSC、CCCC 3种边界下优化获得不同λ时的k*和铺层顺序，如表4、表5所示。表4和表5数据显示，不同边界和载荷工况下，随着λ从0.25增大到1，k*均先快速减小，在λ>1后k*趋于平缓减小，但双轴压组合工况的k*要小于X向轴压组合工况，仅为对应值的0.4～0.8，说明更复杂载荷会弱化层合板的抗屈曲能力。从最优铺层看，组合工况的优化铺层比剪切载荷工况更复杂，仅X向轴压组合工况λ<1时各边界的优化铺层角为正值且相近，而两种组合工况在SSSS和CCCC边界获得的最优铺层角有正有负但绝对值相近；另外，双轴压组合工况CCCC边界λ=1时最优铺层中21°铺层角的出现显得较为特殊。

假如剪切载荷与轴压载荷具有如下比例关系Nxy=βNx(β≥0)，Nx=-1 N，变化载荷比β，优化获得λ=2时两种组合工况下SSSS边界复合材料层合板的屈曲优化结果如表6所示。可以看到，两种工况下，优化铺层随β增大而趋于剪切载荷工况优化结果；在β≥0.3时，k*随β增大而减小且在β≥1处快速下降后降速趋缓，而当β<0.3时，k*表现为非单调变化，存在一个最佳的k*。因此可以在轴压载荷工况中适当匹配剪切载荷来改善层合板的抗屈曲能力。进一步优化不同λ时X向轴压组合工况SSSS边界复合材料层合板，获得k*随β变化曲线如图9所示。图9显示，复合材料层合板的抗屈曲能力整体上随着剪切载荷的增大而降低，除λ=0.5外，仅当β∈(0,0.5)时,k*存在一定的非单调波动；而λ≥2后,λ对k*的影响小到可以忽略。

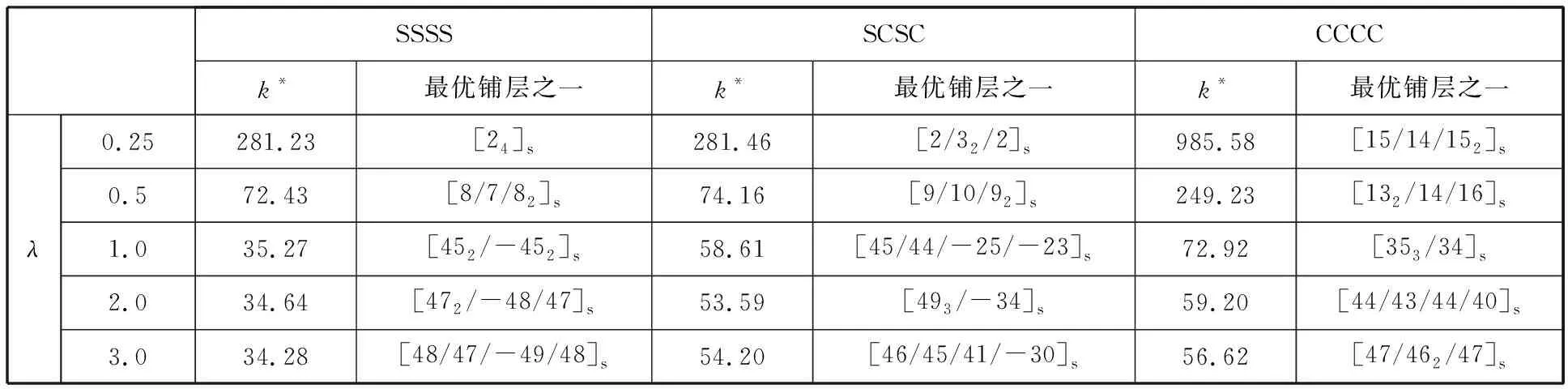
表4 X向轴压组合工况复合材料层合板屈曲优化结果(Nx∶Ny∶Nxy=1∶0∶1)

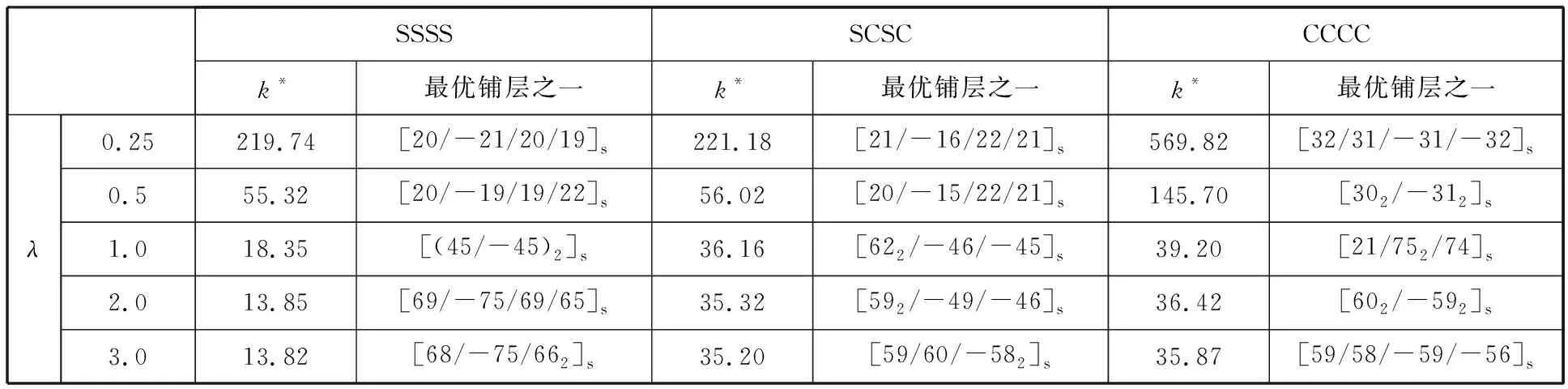
表5 双轴压组合工况复合材料层合板屈曲优化结果(Nx∶Ny∶Nxy=1∶1∶1)

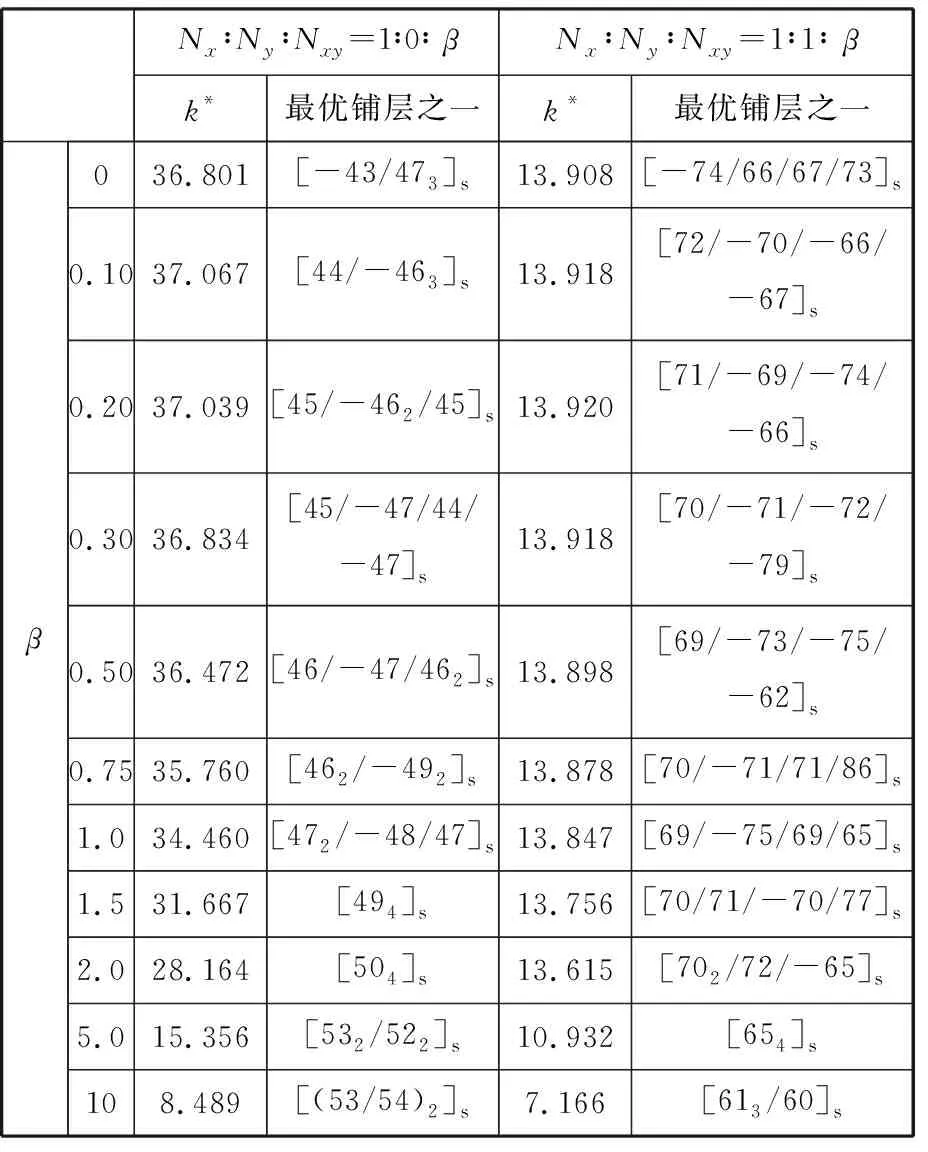
表6 λ=2时SSSS边界复合材料层合板屈曲优化结果

图9 X向轴压组合工况SSSS边界层合板k*随β变化曲线Fig.9 Variation curve of laminate k*with β under SSSS boundary and X axial compression combined loading

4 结论

(1)GDQ法求解复合材料层合板剪切屈曲问题的振荡不收敛的现象源于GDQ载荷矩阵的奇异性，本文提出的权重系数扰动策略能有效改善载荷矩阵的奇异性，实现了扰动GDQ法对层合板剪切屈曲问题的稳定快速求解。

(2)剪切载荷作用时，层合板铺层角对屈曲性能的影响在负剪切载荷时为非凸变化，而在正剪切载荷时为凸变化；层合板铺层数、铺设方式和边界条件对优化铺层角的影响较小，可简化为单变量优化问题；而随着层合板长宽比增大，剪切屈曲性能逐渐减弱，优化铺层角趋于60°。

(3)剪切与轴压载荷组合作用时，除较小的剪切载荷有助于改善层合板屈曲性能外，层合板屈曲性能随剪切载荷增大而减小，优化铺层趋于剪切载荷优化结果，而当层合板长宽比大于2后，剪切载荷对屈曲性能的影响可以忽略。