高速铁路48 m跨度超高性能混凝土简支梁设计及抗弯性能试验研究

刘 琛

(1.中铁第一勘察设计院集团有限公司，陕西 西安 710043;2.轨道交通工程信息化国家重点实验室(中铁一院)，陕西 西安 710043)

根据我国既有铁路和高速铁路常用跨度桥梁建设和运营实践，并通过反复的研究论证,确定我国高速铁路桥梁以等跨布置的预应力混凝土简支箱梁结构为主，主型简支箱梁跨度为32 m，建造方法主要采用沿线设置梁场预制、运梁车运输和架桥机建设[1]。杨宜谦等[2]针对高速铁路32 m简支箱梁的刚度、基频、车桥动力特性等开展相关研究。牛斌[3]对高速铁路40 m 简支箱梁设计参数、足尺试验、运架设备、经济性等开展了理论研究和试验研究。高速铁路32 m整孔箱梁质量一般在850 t左右，郑济高速铁路试制40 m整孔箱梁质量约 1 000 t。简支梁向更大跨度发展，梁质量将显著增加，工程经济性及整孔运架设备能力限制的难题难以解决。

超高性能混凝土(Ultra-high Performance Concrete，UHPC)是一种具有高强度力学性能的混凝土(又称活性粉末混凝土或RPC)。文献[4-6]进行了一系列的UHPC材料和结构的理论研究和试验研究。包括UHPC轴拉性能试验研究、高强钢筋活性粉末混凝土梁抗弯性能试验研究、大跨度活性粉末混凝土简支梁截面形式研究、UHPC薄板屈曲试验研究等。

本文提出48 m UHPC胶拼简支梁主要计算方法并进行理论计算分析，结合1∶2缩尺模型梁抗弯性能试验测试结果，验证其计算方法的合理性，最终提出此类结构的合理设计方法和受力规律，实现利用UHPC力学性能优势，将48 m简支箱梁梁质量控制在850 t以内，为整孔运架简支梁向更大跨度发展提供理论和试验依据。

1 设计参数及计算方法

1.1 UHPC材料设计参数

理论计算及模型梁制作时采用的配合比[7]见表1。预应力UHPC结构浇筑完成后均应进行高温蒸养，试验模型梁采用(40±5)℃恒温养护24 h，箱梁脱模后(70±5)℃蒸汽养护48 h，结构首次加载龄期不小于30 d。UHPC材料力学性能参数主要包括抗压强度、抗拉强度、抗折强度、弹性模量、泊松比、受压和受拉应力-应变关系曲线等。模型梁试验实测UHPC力学参数为:立方体强度fck=120 MPa；轴心抗压强度fc=88 MPa，轴心抗拉强度fct=6 MPa，弹性模量E=44 GPa；重度为26 kN/m3。

表1 UHPC 基体配合比 (kg·m-3)

1.2 桥梁设计参数

速度350 km/h；有砟轨道；线间距5 m，箱梁顶宽12.6 m、梁高4 m；二期恒载180 kN/m；双线ZK活载；冲击系数、离心力、摇摆力制动力按TB 10621—2014《高速铁路设计规范》取值；预应力钢束采用 1 860 MPa 级钢绞线，金属波纹管成孔。

1.3 主要计算方法

48 m UHPC简支箱梁纵向按全预应力结构设计，除按TB 10092—2017《铁路桥涵混凝土结构设计规范》执行外，还应遵循：①对于加载龄期大于4 d的UHPC，高温蒸养48 h后，徐变终极值为0.5[8]，收缩应变终极值为500×10-6。②计入箱梁有效宽度折减系数，跨中及1/4跨为0.97，梁端为0.81。③各种工况下结构稳定安全系数不小于5。④节段拼装接缝面抗弯强度折减系数0.95。⑤接缝正截面抗剪强度依据美国GuideSpecificationsforDesignandConstrmctionofSegmentalConcreteBridges计算。⑥抗裂计算时，UHPC胶接拼装箱梁抗拉极限强度塑性修正系数为0.5。

2 截面形式研究

由于UHPC结构需采用高温蒸养工艺，施工方案设计时宜采用工厂预制，并结合高速铁路桥梁制梁场的布设，对32 m梁制梁场既有蒸养环境的合理改造而避免制梁场建设中过多的经济投入。因此，48 m UHPC简支梁纵向分3段预制，跨中梁段长度16 m，梁端梁段长度16.75 m，见图1。

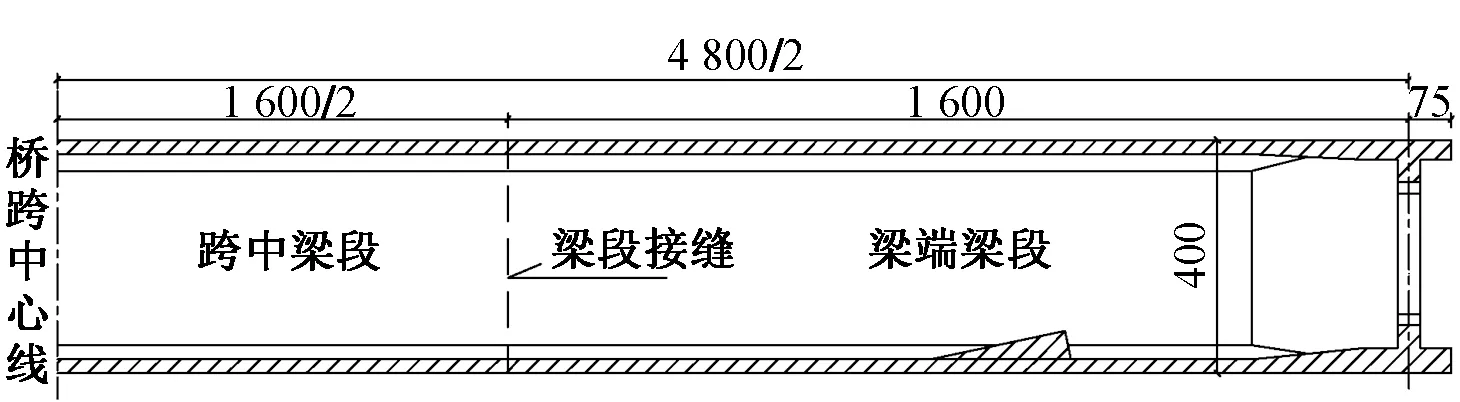
图1 48 m UHPC梁纵向分段示意(单位：cm)

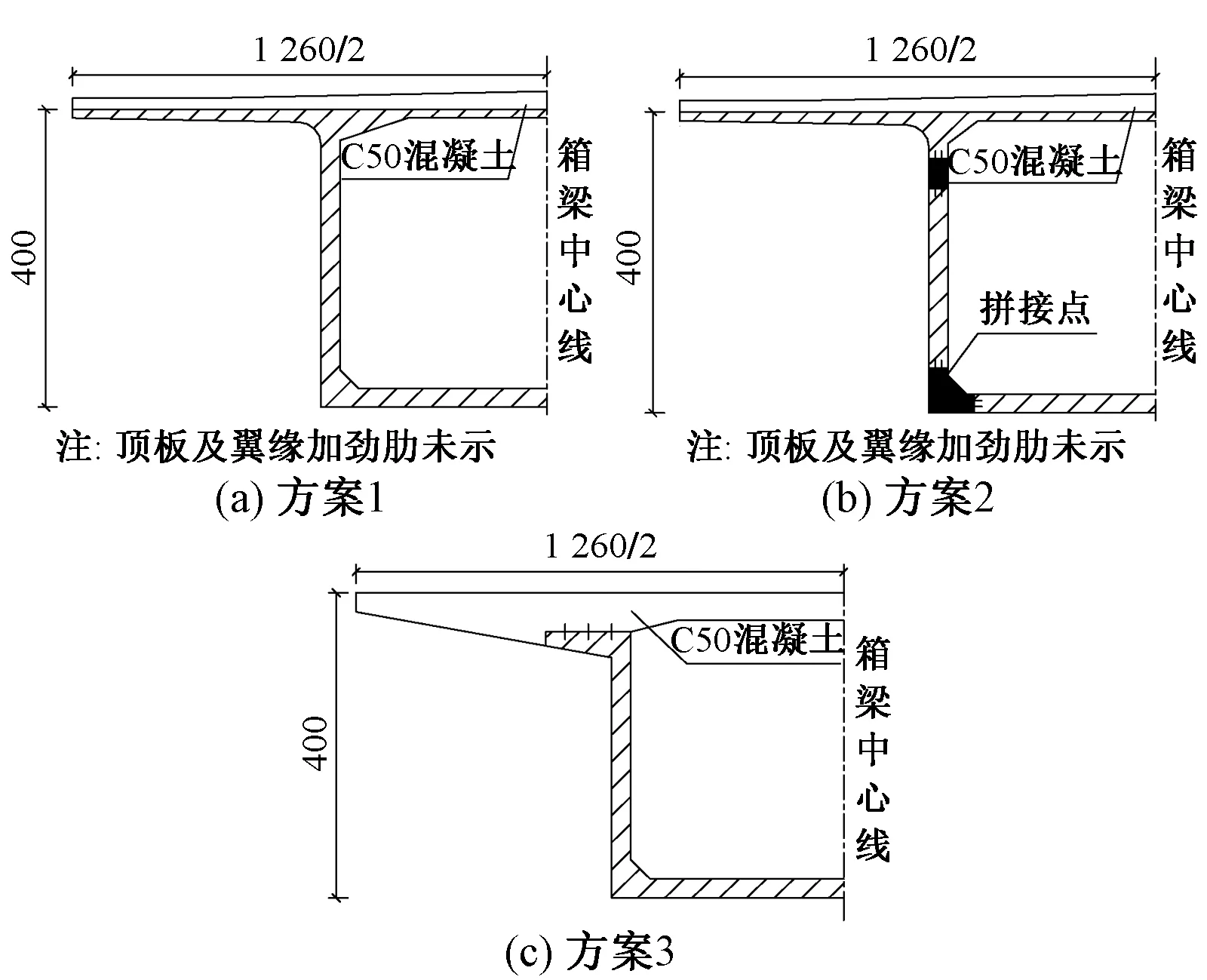
图2 各方案箱梁截面示意(单位：cm)

本次研究48 m UHPC简支箱梁截面形式共3种[9]，如图2所示。图中，方案1为单箱单室UHPC薄壁截面，方案2为单箱单室UHPC拼接板截面，方案3为UHPC与普通混凝土桥面板组合截面。

3个方案结构刚度均能满足要求，方案2刚度最大。方案3组合截面为二次受力结构,U梁应力水平较高，能够发挥材料优势，受力更为合理。施工方案优缺点及经济性比较见表2。可知，尽管方案3受力更为合理，但整孔梁质量达 1 150 t，无法使用高速铁路900 t架桥机进行架设，考虑到运架装备技术能力限制，本次推荐方案1。

表2 各方案施工及经济性综合比较

施工步骤为：梁段预制蒸养→梁段存放→台座上预拼装→接缝面涂环氧胶→张拉顶底板精轧螺纹钢→永久钢束张拉成孔→架桥机架设→现浇C50桥面板→施工桥面设施→成桥。

3 理论分析

3.1 静力计算

48 m UHPC简支梁梁高4.0 m，顶宽12.6 m，底宽6.0 m，顶板厚0.12 m，腹板及底板厚0.25 m。箱梁顶板设置0.15～0.24 m厚C50混凝土桥面板。每孔梁分3个梁段设2处胶接缝。顶板为满足薄板翘曲失稳及架桥机过孔和架梁问题，间距1.5 m左右设置1道横向加劲肋。UHPC梁质量830 t，现浇C50桥面板质量290 t。底板和腹板共布置26束17-7φ5钢束，梁体构造及钢束布置见图3，静力计算主要结果见表3。可知，各项计算值满足TB 10621—2014的要求。

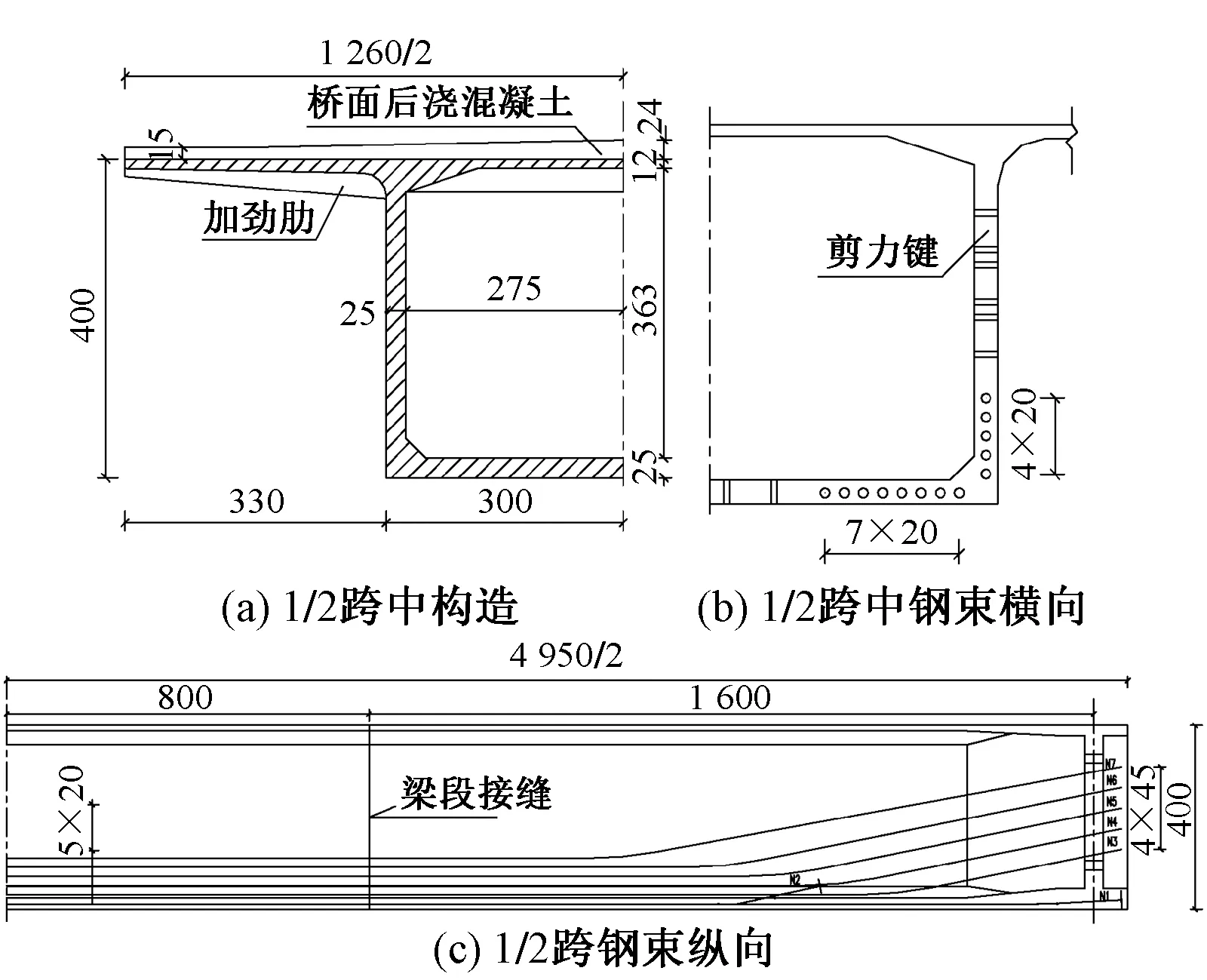
图3 梁体构造及钢束布置示意(单位：cm)

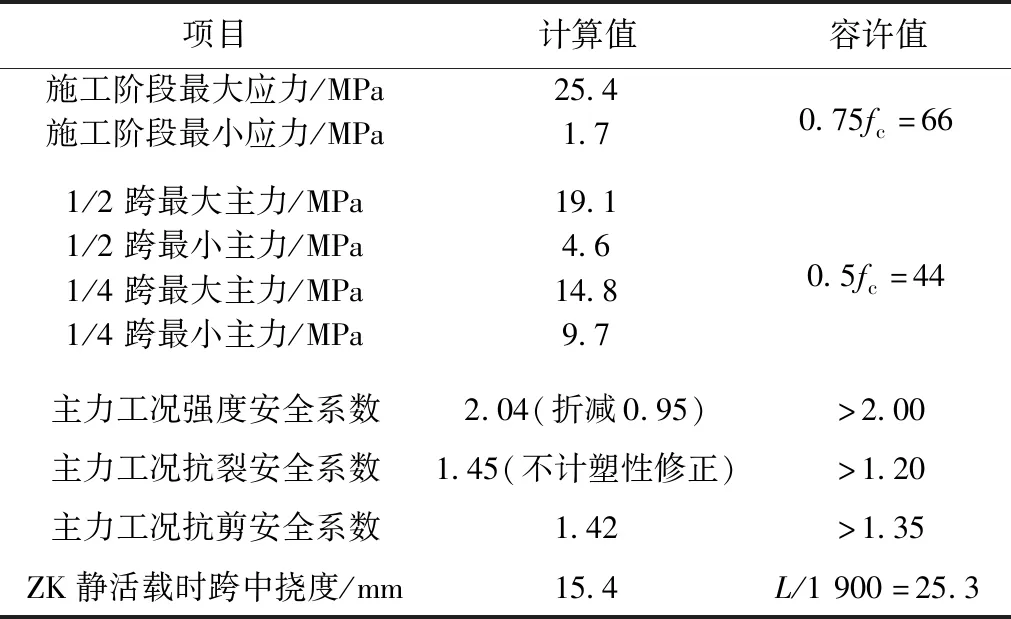
表3 静力计算结果

注：L为跨度。

3.2 动力特性计算

根据规范要求,48 m 简支箱梁竖向自振频率不应小于23.58L-0.592=1.875 Hz。由动力特性计算结果可知，一阶为横向扭转，二阶为竖向弯曲(如图4所示)，对应自振频率2.480 Hz，满足动力特性要求。

图4 动力特性计算(二阶竖向弯曲)

3.3 稳定性计算

箱梁顶板承受较大压应力且厚度较小，为避免薄板结构失稳破坏先于材料强度破坏，对钢束张拉阶段、运架梁阶段、运营阶段进行稳定性分析。施工阶段UHPC梁自重为常量，预应力钢束荷载为变量；成桥后自重及钢束荷载为常量，架桥机及运梁车荷载为变量；运营阶段恒载为常量，活载、温度力等为变量。各阶段屈曲模态见表4。可知，施工阶段稳定安全系数18.5，运营阶段稳定安全系数10.5，均满足规范要求。

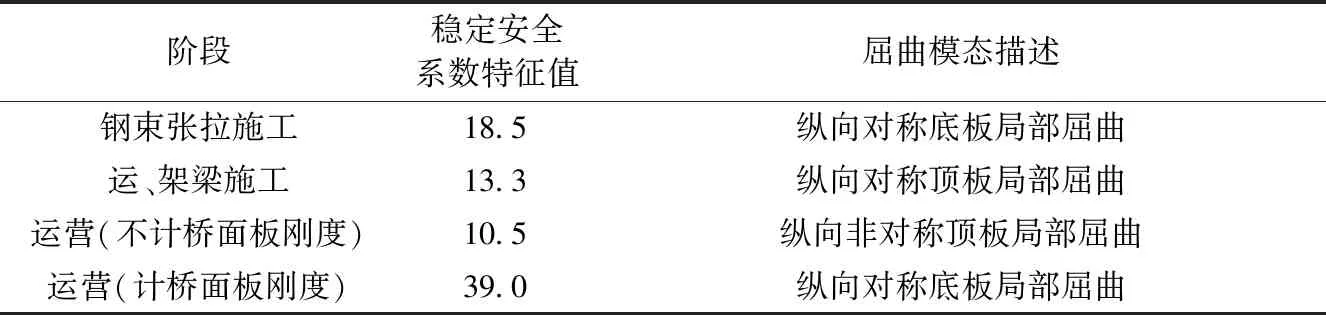
表4 施工阶段及运营阶段屈曲分析

3.4 横向计算

横向计算时考虑加劲肋的影响，施工阶段计算截面为UHPC箱形截面，运营阶段计算计入C50混凝土桥面板对结构受力的影响。横向计算工况共分为：①自重+运梁车;②恒载+双线ZK活载;③恒载+双线ZK活载+日照升温;④恒载+双线ZK活载+寒潮降温。控制截面应力检算结果见表5。可知，工况①顶板跨中下缘超出6 MPa的允许值，需通过布置一定数量的钢筋满足受力要求。

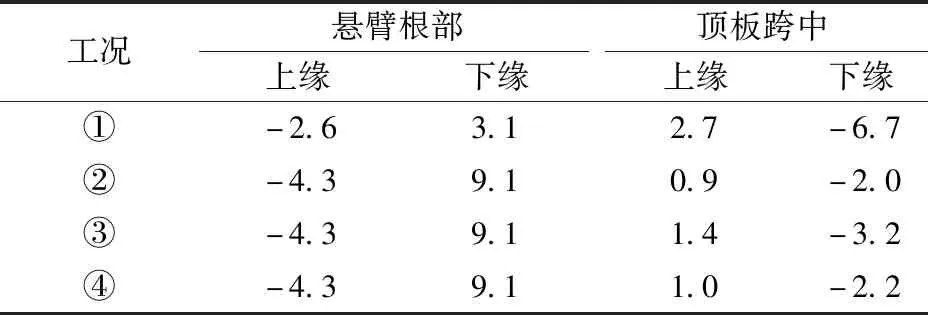
表5 控制截面应力检算结果(拉为负，不计钢筋影响)MPa

4 缩尺试验研究

4.1 模型梁设计

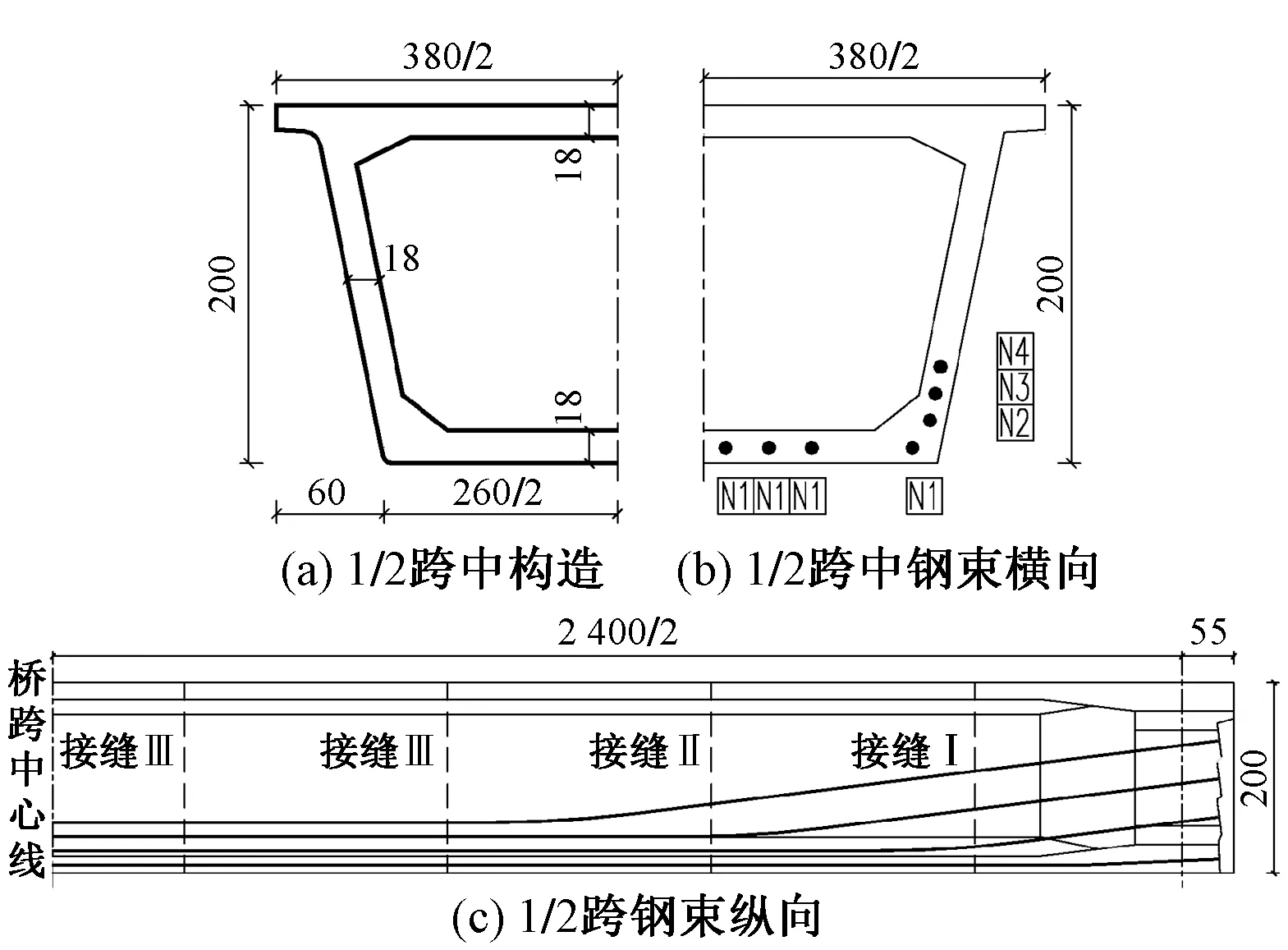
图5 48 m UHPC梁1∶2缩尺模型梁构造及钢束示意(单位：cm)

对整孔运架48 m UHPC简支梁开展薄壁箱梁模型试验，验证设计参数和计算方法的合理性。模型梁为1孔24 m单箱单室箱梁并按照1∶2缩尺设计、制作和测试。48 m UHPC梁1∶2缩尺后跨度24 m，梁高2 m，取消悬臂板后顶板宽度3.8 m，顶底板及腹板厚度按波纹管构造控制为0.18 m,底板和腹板共布置14束7-7φ5钢束，分为9个预制梁段，采用胶拼施工。模型梁构造及钢束布置见图5，48 m UHPC简支梁与模型梁设计荷载对比见表6，主要计算结果见表7。可知，各项计算值满足TB 10621—2014的要求。

表6 48 m UHPC工程梁与模型梁设计荷载 (kN·m-1)

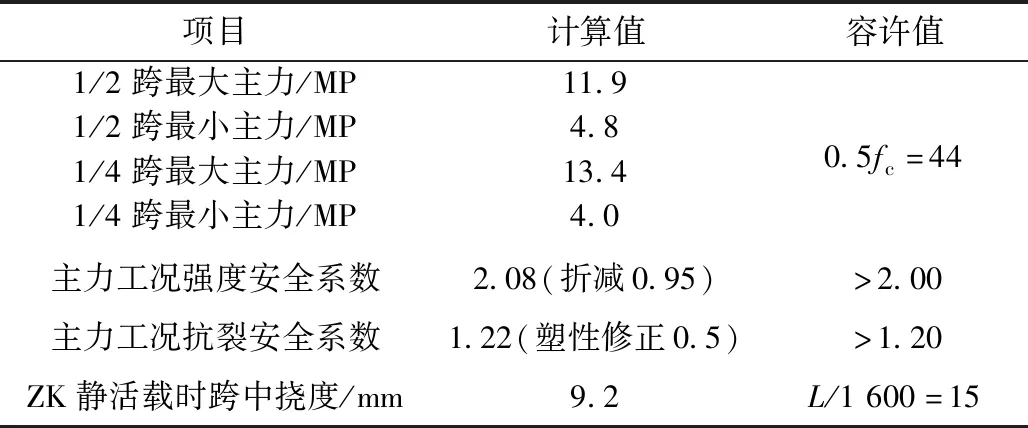
表7 主要计算结果

注：L为跨度。

4.2 试验方案

加载方案采用纵向5点加载[10]，反力架纵向间距4 m，横向采用2点加载，加载点作用于箱梁腹板中心处顶板，跨中截面布置20个纵向振弦式应变传感器测点采集数据，见图6。测试内容包括预应力张拉测试、动力特性、荷载挠度曲线、不同荷载下应力应变规律、裂缝的分布、发展规律等。静载试验最大加载至971 kN，对应单点加载值为 1 039 kN，等效跨中加载弯矩 37 386 kN·m。

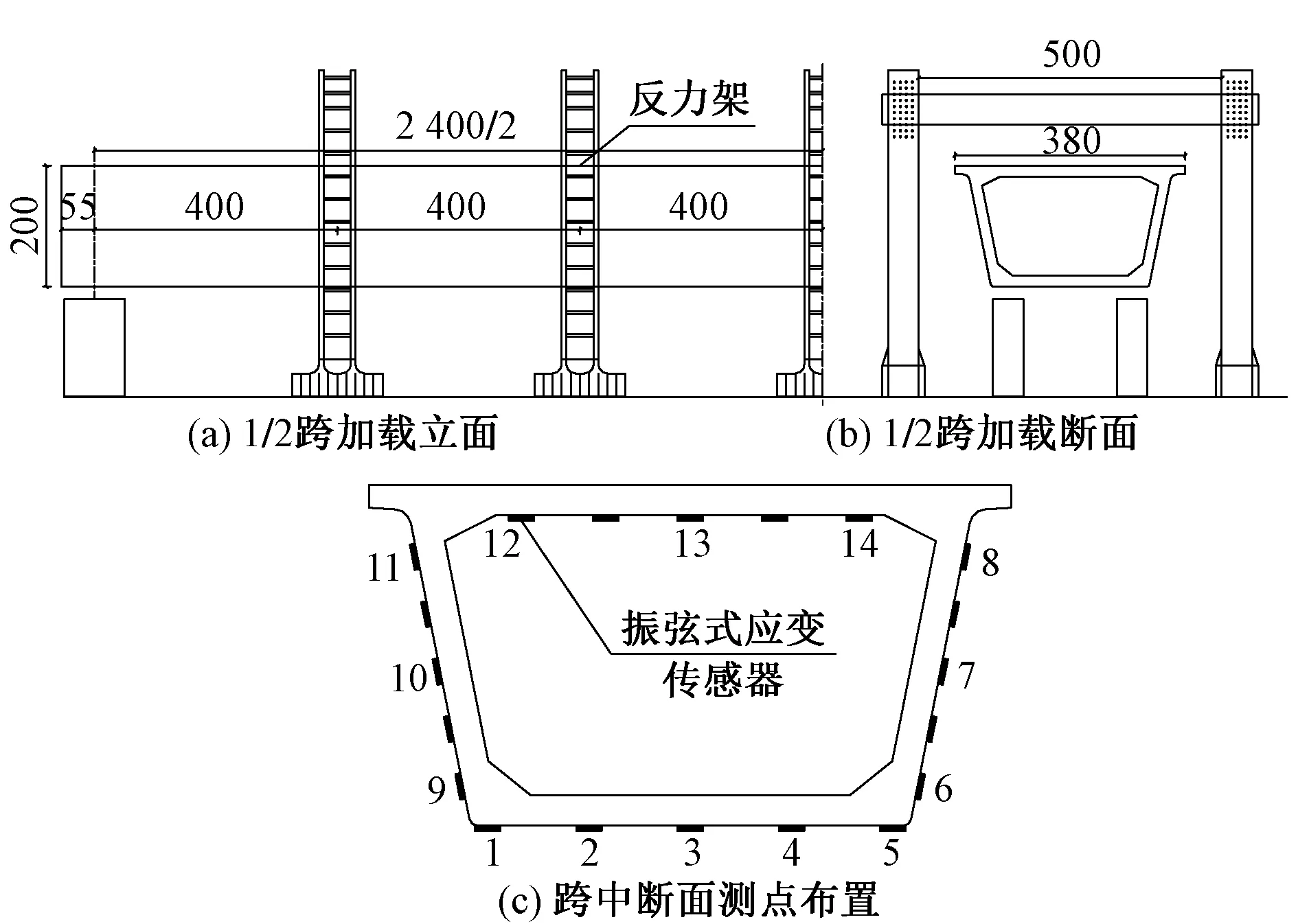
图6 模型梁静载试验加载示意(单位：cm)

4.3 试验现象及结果分析

破坏荷载2次加载过程中，试验加载值与UHPC模型梁的变形及与应变关系见图7。可知：①加载至574 kN，挠度变化平稳，卸载后挠度变形基本恢复至初始状态，随后加载挠度变化加快。②第1次加载至574 kN，跨中截面中性轴在 1 100 mm 左右，跨中底板UHPC应变与加载值呈线性关系，测试位置处于弹性状态；加载至618 kN之后，跨中胶缝开裂，中性轴开始移向受压区；加载至971 kN，腹板实测中性轴最高为 1 445 mm；第2次加载由于跨中底板和南侧腹板裂缝逐渐开展，中性轴变化与第1次不同。③加载至640 kN，跨中节段两端的胶缝先开裂；加载至751 kN，距离跨中1.5倍节段长度胶缝开裂，其他胶缝未开裂，梁体未发现可见裂缝；加载至832 kN以后，南侧底板逐渐出现混凝土裂缝，跨中偏西的部分混凝土测点(4,5,6)应变急剧增大。④加载过程中，跨中顶板应变随着加载值变化平稳，加载至971 kN，平均应变507×10-6，模型梁压区混凝土受力安全。

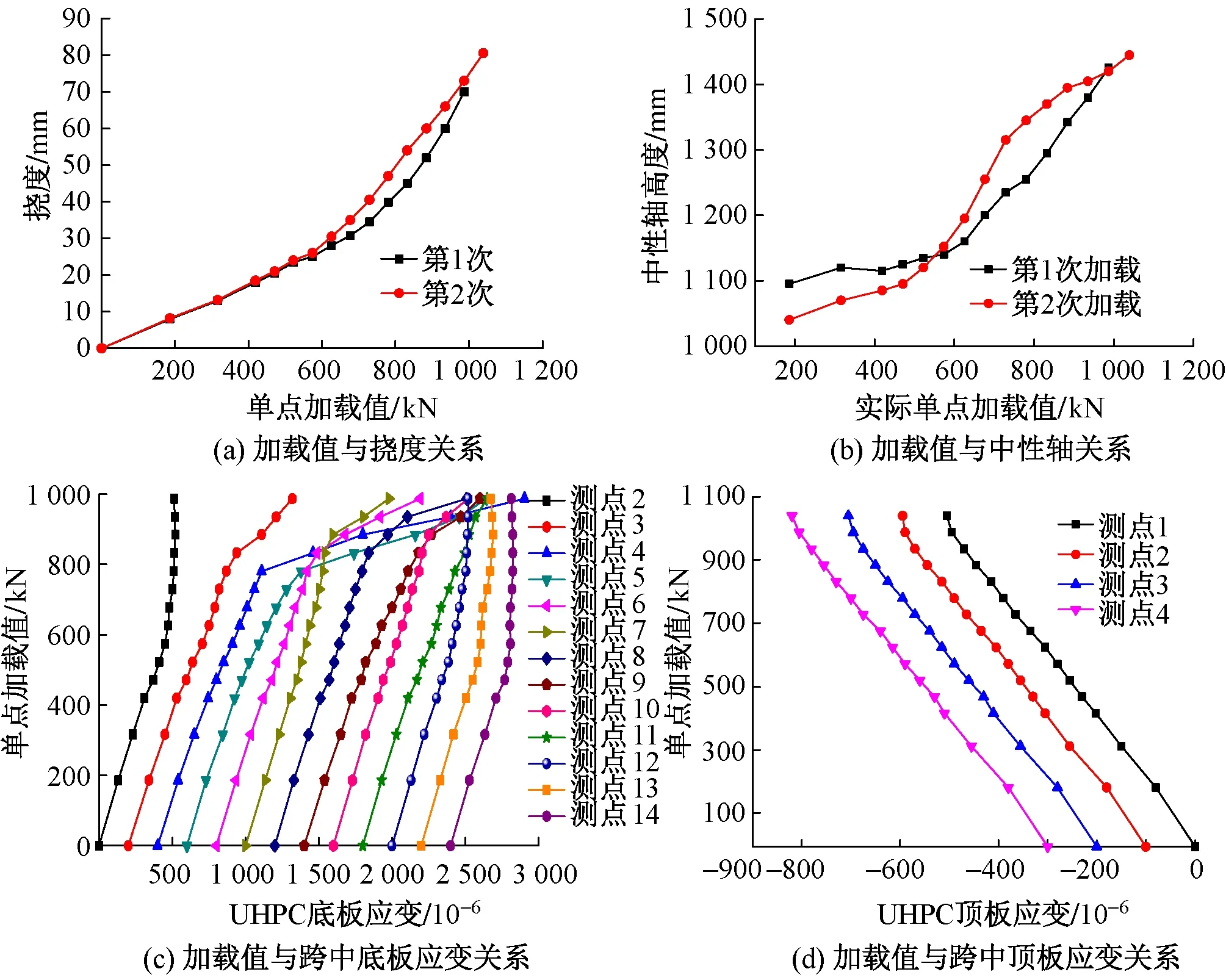
图7 试验加载值与变形、应变关系

24 m UHPC模型梁主要理论、试验结果见表8。可知，使用实测结构变形、应力状态等与理论计算结果基本相符。

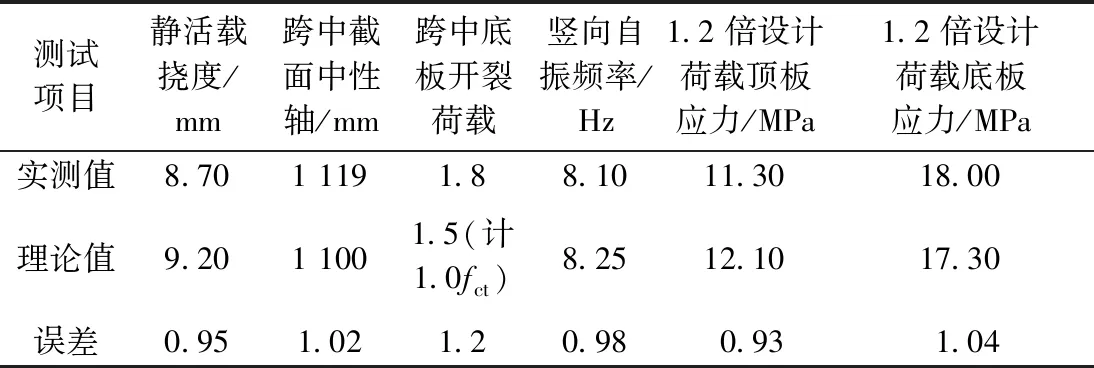
表8 24 m UHPC模型梁主要理论、试验结果

UHPC 24 m跨预应力模型箱梁设计、施工、试验满足各项要求，开裂前模型梁处于弹性工作状态，且试验实测结构变形和应力状态等参数与理论计算基本相符。抗裂安全系数实测值与理论值偏差较大,达1.2倍。

环氧树脂接缝拼装梁抗裂系数计算公式为

(1)

(2)

式中：Kf为抗裂安全系数；σc为扣除预应力损失后的预压应力；γ为混凝土塑性修正系数；σ为外荷载在截面受拉边缘产生的拉应力；S0为换算截面重心轴以下的面积对重心轴的面积矩；W0为对所检算的拉应力边缘的换算截面抵抗矩。

根据式(2)计算UHPC塑性修正系数γ理论值为1.3,此时按式(1)计算抗裂安全系数为1.55。对于本试验梁实测抗裂安全系数1.80，推算塑性修正系数γ为1.5。影响抗裂系数差异较大的原因为UHPC的塑性修正系数取值。

5 结论

1)高速铁路48 m UHPC箱梁通过理论分析各项技术指标满足规范要求，整孔梁质量控制在830 t可实现整孔运架。运架装备改造理论可行，后期还应开展运架装备研究。

2)提出高速铁路UHPC节段预制、胶接拼装简支箱梁主要的设计参数和计算方法，并制作24 m跨度的UHPC箱梁开展抗弯性能试验研究。

3)UHPC模型梁抗弯性能试验表明：开裂荷载前模型梁为弹性工作状态，理论计算与试验结果吻合较好。开裂荷载至破坏荷载加载，挠度变化加快，加载至破坏荷载，顶板平均压应力22.3 MPa，模型梁仍受力安全。

4)UHPC箱梁抗裂系数理论值小于实测值，结构偏于安全。一般抗裂计算可参考本试验梁的UHPC塑性修正系数1.5或根据具体试验结果调整。