关联的无证书环签名方案*

刘纯璐 ，游 林

（1.杭州电子科技大学 通信工程学院，浙江 杭州 310018；2.杭州电子科技大学 网络空间安全学院，浙江 杭州 310018）

0 引 言

2001年，环签名由Rivest等人[1]首次提出，允许签名者在保持匿名的情况下代表所有环成员对消息进行签名。签名者任意选取n个成员公钥，结合自己的私钥就可以生成一个首尾闭合的环状签名，起到保护签名者隐私的作用。它在需要长期保存信息的一些特殊应用中非常实用，但却为违法犯罪分子的不良行为提供了庇护。为此，针对具有关联性、可追踪性等特殊性质的环签名研究为更多的实际应用场景提供了可能。2003年，Al-Riyami等人[2]首次提出无证书公钥密码体制。用户从自己的基本信息中提取公钥，随机选择秘密值与密钥生成中心（Key Generation Center，KGC）为用户生成的部分密钥结合生成相应的私钥。从而有效地简化了传统公钥密码体制的证书管理问题，也避免了基于身份的公钥密码体制[3]的密钥托管问题。

2014年，Liu等人[4]提出了一个具有无条件匿名性的关联的环签名方案，该方案在环签名的基础上添加关联参数，由此可以判断任意两个签名是否由同一个签名者签发。2017年，Zhang等人[5]将环签名与无证书公钥密码学相结合，提出了具有三个双线性对运算的无证书环签名方案。2018年，Gu等人[6]在标准模型中提出了一个可追踪的无证书环签名方案。本文提出了一个新的关联的无证书环签名方案，在保证高效率的同时实现了安全模型下的可证明安全。

1 关联的无证书环签名方案

关联的无证书环签名方案的合法参与者包括KGC、n个签名者、签名验证者和关联验证者，由系统初始化、部分密钥生成、秘密值生成、私钥生成、公钥生成、签名生成、签名验证和关联验证8个函数组成。其中，图1描述了方案的密钥生成过程以及图2描述了方案的模型流程图。

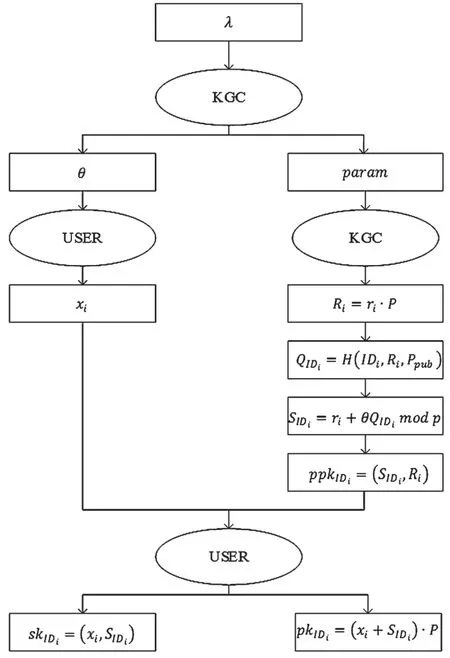
图1 密钥生成过程

图2 关联的无证书环签名方案模型

（1）系统初始化：输入安全参数λ，KGC选取素数阶为p的循环加法群G，P是G的生成元。随机选择主密钥计算系统主公钥并且将和作为三个系统哈希函数。最后，将系统公共参数集合公开，并且秘密保存系统主密钥θ。

（2）部分密钥生成：输入用户身份IDi、θ和param，KGC随机选择ri∈Zp*，计算Ri=riP，Qi=H(IDi,Ri,Ppub)和Si=ri+θQimodp。然后，KGC将用户的部分私钥ppki=(Si,Ri)通过安全渠道发送给用户。通过检验Ri+QiPpub=SiP等式是否成立，用户可以验证部分密钥的正确性。

（3）秘密值生成：输入param和IDi，用户随机选取为秘密值。

（4）私钥生成：用户生成私钥ski=(xi,Si)。

（6）签名生成：该函数由身份为IDπ的签名者运行，输入参数集合(event,n,PK,skπ,m)。其中，参数分别表示事件event、环的大小n、公钥集合PK=(pk1,pk2,…,pkn)、签名者私钥skπ以及消息m。签名者私钥为skπ=(xπ,Sπ)，计算如下：

1）计算e=H´(event)，t=xπe；

2）取rx,ry,c1,…,cπ-1,cπ+1,…,cn∈R Zp*，并计算：

3）为了得到cπ的值，计算c1+…+cnmodp=H´(PK||event||t||m||K||K´)；

（7）签名验证：输入参数集合(event,n,PK,δ)，计算验证等式是否成立。若成立，则输出“TURE”，否则，则输出“FALSE”。

（8）关联验证：输入 (event1,n1,PK1,m1,δ1)和(event2,n2,PK2,m2,δ2)，分别对其检验签名的有效性。若δ1=(t1,·)和δ2=(t2,·)都为有效签名，且t1=t2，则两个签名“关联”，否则，“不关联”。

2 安全性证明

我们将基于椭圆曲线离散对数困难问题，在随机预言模型中证明关联的无证书环签名方案针对第Ⅰ类型敌手AⅠ和第Ⅱ类型敌手AⅡ都具有不可伪造性的安全特性。

定理2.1：基于离散对数问题是困难的假设前提下，在随机预言机模型中关联的无证书环签名针对第Ⅰ类型敌手AⅠ具有不可伪造性。

证明：假设AⅠ具有不可忽略的优势ε1来攻破我们提出的方案。我们要证明多项式时间函数挑战者B能够利用AⅠ来解决离散对数问题，即根据已知随机实例(P,xP)来确定x的值。

在系统初始化阶段，B输入一个安全的参数λ，输出主密钥θ和系统公共参数集合param。B将param=(G,p,H,H´,H´,P,Ppub)发送给AⅠ，另外秘密保存θ。

（1）H´哈希值查询：对于H´哈希值的查询，挑战者B随机选择计算并返回αP的值。

（2）H、H´哈希值查询：对于未分配的哈希值查询，B随机选择并返回。

（3）部分密钥查询：当AⅠ查询身份为IDi用户的部分密钥，其中被查询用户的身份IDi不是目标身份IDⅠ。B首先随机选取正整数计算得Ri=siP-hiPpub。然后，B返回部分密钥ppki=(Ri,si)给AⅠ。

（4）秘密值查询：当AⅠ查询用户的秘密值，B将随机选取并返回给AⅠ。

（5）公钥查询：当AⅠ查询身份为IDi用户的公钥，其中被查询用户的身份IDi不是目标身份IDⅠ。B首先进行秘密值查询和部分密钥查询，然后计算得pki=(xi+Si)P。

（6）公钥替代查询：当AⅠ对用户的公钥pki进行公钥替代查询，B可以实现将pki´替代原公钥pki。

（7）环签名查询：当AⅠ对输入的参数集合(event,n,PK,skπ,m)进行环签名查询，B将进行以下过程：

1）如果H´(event)未赋值，首先对事件event运行哈希查询H´，计算得到e=H´(event)=αP，并计算得t=xπe。

3）B输出签名

如果AⅠ为身份为IDⅠ的目标用户以不可忽略的概率优势ε1成功输出环签名这说明B至少能以1/qH×(1-1/qH)qn×ε1的优势解决椭圆曲线离散对数问题，其中qH代表对哈希查询H进行的最大查询次数，qn代表对部分密钥查询的最大查询次数。然而，这与椭圆曲线离散对数问题困难假设相矛盾，即AⅠ无法为目标用户以不可忽略的概率优势ε1成功输出

定理2.2：基于离散对数问题是困难的假设前提下，在随机预言机模型中关联的无证书环签名对第Ⅱ类型敌手AⅡ具有不可伪造性。

证明：假设AⅡ具有不可忽略的优势ε2来攻破关联的无证书环签名方案。我们要证明多项式时间函数B能够利用AⅡ来解决离散对数问题，即根据已知随机实例(P,xP)来确定x的值。

在系统初始化阶段，输入一个安全的参数λ，输出系统主密钥θ和系统公共参数集合param。然后，B将param=(G,p,H,H´,H´,P,Ppub)和θ通过安全信道都发送给AⅡ。

在这整个过程中，哈希查询、公钥查询、环签名查询的细节与上述定理2.1的证明过程相同。但是，AⅡ具有主私钥θ，可以自主计算出部分私钥ppki。如果AⅠ为身份为IDⅠ的目标用户以不可忽略的概率优势ε2成功输出环签名δ*={t*,x~*,y~*,c1*,…,cn*}。这说明B至少能以 1/qH×(1-1/qH)qm×ε2的优势解决椭圆曲线离散对数问题，其中qH代表对哈希查询H进行的最大查询次数，qm代表对秘密值的最大查询次数。然而，这与椭圆曲线离散对数问题困难假设相矛盾。

3 性能分析

我们从运算代价和性能将本方案与同类型签名方案进行对比，比较结果如表1所示。为方便起见，我们将E表示指数运算，M表示多次幂指数运算，其运算代价约E的1.3倍，P表示双线性对运算，TE表示椭圆曲线上的标量乘法运算，以及TPO表示基于配对的标量乘法运算。

表1 签名方案性能比较

由上表可知，同类型签名方案的运算代价主要集中在证书管理以及签名和验证运算过程中。在Liu等人[4]提出关联的环签名方案中，证书管理的开销会随着环成员的增加而呈线性增长。Gu等人[6]提出可追踪的无证书环签名方案需要大量的双线性计算，而双线性对计算会造成很大的运算代价。相较于其他两个方案，我们的方案在整个签名运算过程中克服了证书管理问题，减少对可信第三方的依赖程度，并且降低了双线性对计算100%的运算量。

4 结 语

本文在无证书环签名算法的基础上添加关联参数，在随机预言机模型中提出了一个具有高安全性和低运算量的关联的无证书环签名方案。在椭圆曲线离散对数问题是困难的假设前提下，我们针对该方案在选择消息攻击下的两种典型攻击进行了验证，结果表明该方案具有不可伪造性。在整个运算过程中，主要的运算量集中于证书管理和双线性对计算。与同类型的签名方案相比，我们提出方案克服了证书管理问题，并且降低了双线性对计算100%的运算量，运算效率有显著的提升，在电子选举、数字货币等网络环境中得到着更好地应用。