聚类回归分析在降雨量统计数据中的应用

昌 霞 刘赛娥

（云南国土资源职业学院 昆明 650000）

1 引言

聚类分析是将物理或者抽象对象的集合分成相似的对象类的过程［1］。回归分析根据研究对象和目的，确定哪个是自变量（解释变量），哪个是因变量（被解释变量）研究变量之间的依存关系，通过建立回归模型和控制自变量来进行估计和预测［2］。比如说，从相关分析中我们可以得知某些变量密切相关，但是那几个是最重要的，相互影响程度如何，则需要通过聚类回归分析方法来确定［1］。在降雨量统计数据中，我们主要得到的是“时间”和“雨量”密切相关，地理位置、人为因素、气温等因素也对降雨量有着一定影响，本文就昆明市西山区28个监控点数年来降雨量统计数据来做分析。

2 研究区域概况

昆明市西山区地形地貌特殊，区境内山恋起伏、山高谷深、岸悬流急、溪流切割强烈，共有14个小流域，其间分布着多个山洪危险区及数量众多的滑坡灾害点。根据西山区实测降水资料显示，每年的雨季5月至10月降水量即占全年降水量的80%以上，再加上各小流域多为山区性特小流域，面积小、河长短、河道比降大，洪水均由暴雨造成，具有陡涨陡落的山区河流的洪水特性，因此遇到较大降水，极易引发山洪、泥石流等山洪灾害。在统计数据中，样本点的分布显得尤为重要，本文就昆明市西山区近年来降雨统计数据进行采样、清洗及分析。

3 聚类回归分析方法

定量分析是依据统计数据，建立数学模型，并用数学模型计算出分析对象的各项指标及其数值的一种方法［2］。它既保留重视观察实验、收集经验资料的特点，又保留重视逻辑思维演绎推理的特点，应用假说使得观察实验方法和数学演绎形式结合起来［3］。正因为这样，定量分析往往比较强调实物的客观性及可观察性，强调现象之间与各变量之间的相互关系和因果联系［2］。

3.1 聚类分析

聚类是找出数据库中的一组数据对象的共同特点并按照分类模式将其划分为不同的类，其目的是通过分类模型，将数据库中的数据项映射到摸个给定的类别中［4］。可以应用到涉及到应用分类、趋势预测中，针对数据的相似性和差异性将一组数据分为几个类别。属于同一类别的数据间的相似性很大，但不同类别之间数据的相似性很小，跨类的数据关联性很低。

系统聚类方法中比较典型的是Ward方法。Ward即离差平方和法。它主要体现在同类离差平方和较小，类间偏差平方和较大。

3.2 回归分析

“回归”（regression）是由英国著名生物学家兼统计学家高尔顿（Francis Galton）在研究人类遗传问题时提出来的［5］。回归分析反映了数据库中数据的属性值的特性，通过函数表达数据映射的关系来发现属性值之间的依赖关系［6］。它可以应用到对数据序列的预测及相关关系的研究中去。设因变量y与自变量x1，x2，……，xk之间有关系式：

通过取样得到n组观测数据：

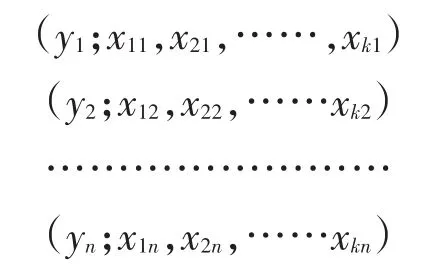
其中xij是自变量xi的第j个观测值，yj是因变量y的第j个值，代入上式得到模型的数据结构式：

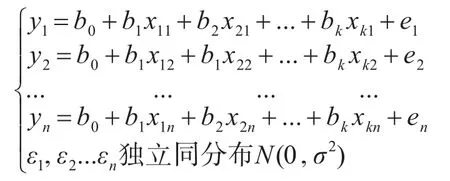
上述方程式为k元正态线性回归模型，其中b0，b1，…，bk及σ2是未知待估的参数［7］。

4 数据分析

4.1 多元回归模型的拟合

从相关分析角度来说，研究一个变量与多个变量的线性相关称为复相关分析（analysis ofmultiple correlation）［5］。复相关中的变量没有因变量与自变量之分，但是在实际应用中，复相关分析经常与多元线性回归分析联系在一起，因此，复相关分析一般指因变量y与 k个自变量x1、x2、…、xk的线性相关［8］。

多元线性回归模型也需要符合多元回归的高斯假设条件［8］。本文采用最小二乘法来估计回归系数 b0，b1，…，bk。

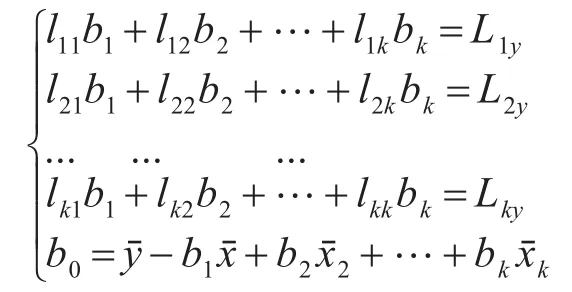
方程组有解，便可得b0，b1，…，bk的最小二乘估计。

计算所有已知站点间的距离，利用微积分知识使用SPSS工具来求解上式方程组，省略去随机项即可得到多元线性回归方程：Y=0.008+1.061x1+0.087x2+0.157x3-0.365x4-0.105x5-0.017x6。通过异常值检验进行残差分析，实验点的标准化残差都落在（-2，2）区间以内。

4.2 W ard法聚类

Ward'smethod是凝聚法分层聚类中一种度量cluster之间距离的方法。按照这个方法，任意两个cluster之间的距离就是这两个cluster合并后新cluster的 ESS［9］。

Ward方法并类时总是能使得并类的类内离差平方和增量最小［10］。对应的公式为

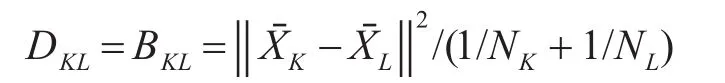
递推公式为

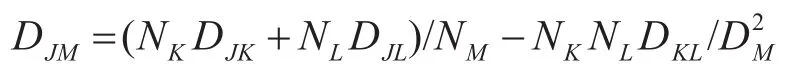
图1给出采用Ward法聚类得到的各站点的降雨量信息树状图。可以看到站点降雨量差异性分布。

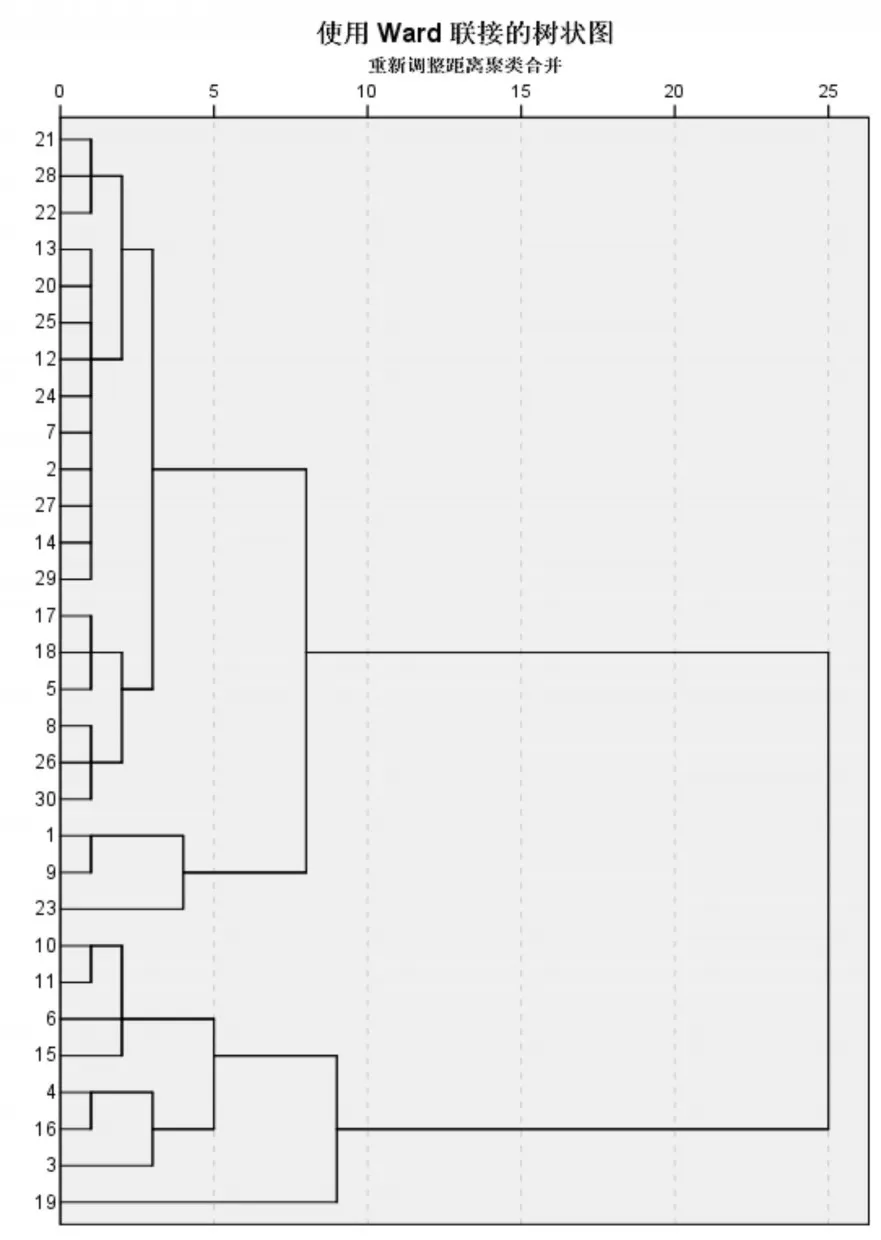
图1 Ward法聚类树状图

4.3 K-mean聚类

K-mean聚类是用户指定类别数的大样本资料的逐步聚类分析［10］。所谓逐步聚类分析就是先把被聚对象进行初始分类，然后逐步调整，得到最终K个分类［10］。该方法需要事先设定分类的个数，并不适合没有先验知识的条件下的数据聚类［11］。另外，K-mean法对离群点较为敏感，即采样点离散度越高，聚拢性越弱；数据分布容易被扭曲［11］。

本文将数据导入SPSS中，根据系统聚类法的经验将K选择为5。迭代次数和系统聚类一样选择25次。表1是K-mean的迭代历史记录，可以看出由于聚类中心内没有改动或改动较小而达到收敛［12］。表2是随机选取5个站点的数据来验证其有效性。每个聚类样品数表。下面输出和解释K-mean聚类结果。

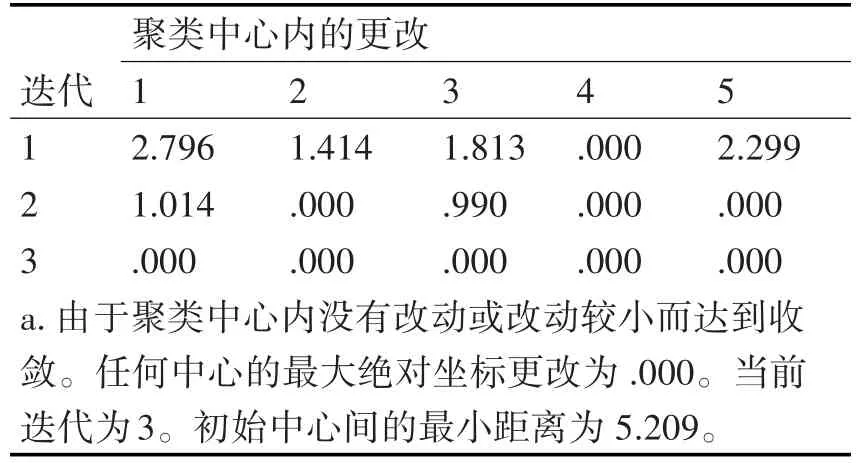
表1 迭代历史记录

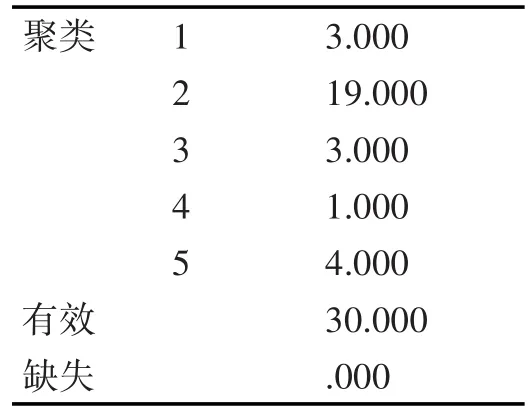
表2 聚类样品数

表3是K-mean聚类的各个类的具体成员，距离代表的是样品与设定参考值的残差比。最后看到分类结果与Ward法有所相似，但是组内距离较大，实际效果不如Ward法。分类特征也不够明显，无法凸显各个站点降雨量差异性的特点［12］。但是我们可以看到海口、石码哨与其他站点的降雨量信息和其他站点有些不同，在其他方法中也显现出来。

表3 聚类成员

5 结语

本文通过对西山区28个监控点来实现回归分析和聚类分析。回归分析得到一个拟合度良好多元线性回归方程，并进行了残差分析。聚类分析通过比较系统聚类方法——Ward法聚类和K-mean方法的不同。在处理该批数据的这两种方法中，以Ward法更为理想。Ward法所做的聚类得到组间距离最大，组内距离最小［13］。中部雨量站集中在第一聚类中，南部雨量站集中在第二聚类中，北部雨量站集中在第三聚类中。可以看出，得到的聚类结果有明显的地理位置聚拢性，十分符合实际情况，即地理位置较近的地方，降雨量差异性较小。