基于固态发酵温度的曲线特征提取算法及应用*
陈 树 张继中
(江南大学物联网工程学院 无锡 214122)
1 引言
白酒发酵过程中的温度影响酵母菌的生长繁殖进而影响白酒的产量[1~2],入窖水分含量、入窖酸度和入窖淀粉浓度也会影响白酒的产量[3~5]。为了提高白酒的出酒率,本文用支持向量机对这些影响因素进行分类。每个窖池一个周期的温度数据有一千多个,而相应的入窖水分、入窖酸度、入窖淀粉的数据均只有一个,这样会导致入窖水分、入窖酸度和入窖淀粉的权重太小甚至可以忽略,所以本文要对发酵过程中的温度数据进行降维处理,发酵过程中的温度随时间呈曲线形式变化,可以提取发酵温度曲线的曲线特征来代替发酵温度数据。
目前关于曲线特征提取的研究有很多。有的采用链码描述曲线:赵宇等提出了一种夹角链码方法,用有向等长的线段代替曲线,得到一序列相邻线段形成的夹角,结果表明匹配效果好[6];张永梅等提出了改进的变长夹角链码方法,表述了弯曲程度较大的拐角,用直线替代了变化幅度较小的曲线[7];余博等提出了描述曲线拐角点的Freeman链码描述方法[8]。有的基于傅里叶变换描述曲线:祁友杰等提出了辨别非闭合曲线的傅里叶描述方法,解决了传统傅里叶算法应用于非闭合曲线的结果偏差问题,有着更好的匹配性能[9];聂雪华等提出了选用傅里叶描述子提取平面连杆曲线的特征,实验表明该方法精度高,节约了数据的存储空间[10]。有的建立趋势集合描述曲线:李翔等提出了一种新的特征提取算法,考虑到轨迹变化趋势,对趋势集合进行判别,有效排除了干扰,优化了匹配效率和准确率[11]。
上述算法都对曲线进行了特征提取,很好地描述了曲线。为了将发酵温度曲线的全局特征提取出来,精确地描述发酵温度曲线,本文引用相对高度的定义,借鉴其中的思想,提出了一种曲线特征提取算法,将每个窖池一个周期的发酵温度曲线特征提取出来,在二叉树的根节点中存放相应的相对高度,用相对高度组成的特征信息描述温度曲线,然后将曲线特征加入窖水分、入窖酸度、入窖淀粉组成新的特征,用支持向量机对新的特征分类,分类正确率更高。根据分类情况,优化下一轮入窖的前置条件,更精确地控制配料比例,使其达到更好的发酵状态。
2 本文的曲线特征提取算法
本文引用了文献[12]中相对高度的定义,如图1(a)所示,且是曲线上的点离线段 AB的最大距离,则曲线 AB的相对高度为。

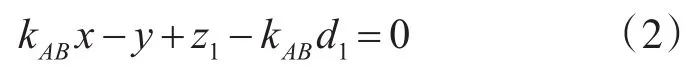
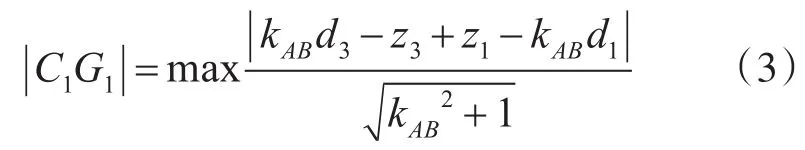
曲线相对高度的大小说明了曲线弯曲程度的高低,相对高度越大,曲线弯曲程度越高,反之,曲线弯曲程度越低。
发酵温度曲线都是开曲线,且不存在平移、旋转等变化情况。本文曲线特征提取的算法步骤如下:
2)由1)知,点G1将曲线 AB分成曲线 AG1和BG1,对于曲线AG1,算出发酵温度曲线的两点A和G1的距离以及曲线AG1上离直线AG1最远的点 G21(如图1(b)所示),得出曲线 AG1的相对高度h2,将h2放在二叉树第二层左子树的根节点上。对于曲线BG1,算出发酵温度曲线的两点B和G1的距离以及曲线BG1上离直线BG1最远的点 G22(如图1(b)所示),得出曲线 BG1的相对高度h3,将h3放在二叉树第二层右子树的根节点上。
3)由步骤2)的分析,以此类推,曲线 AB会被G分成多个曲线,通过计算得到多个相对高度,对每个曲线段均从左到右遍历,将对应的相对高度从左到右依次放在二叉树根节点的下面子节点上,直至相对高度h<ε(ε为足够小的正数)。

图1 曲线特征提取过程
由曲线特征提取算法步骤可得到各曲线段对应的相对高度,图1(b)中曲线 AB 、AG1、BG1、AG21、G1G21、G1G22和 BG22对应的相对高度分别为 h1、h2、h3、h4、h5、h6和 h7,将各曲线的相对高度存放在对应的二叉树根节点上,即二叉树前三层的根节点,如图2所示。

图2 二叉树前三层的根节点
3 支持向量机
本文采用径向基核函数(Radial Basis Function,RBF),RBF核函数为

核函数将向量x从输入空间Rn按照一定的规则映射到某个特征空间Γ的变换K,则SVM的最优判别函数为

4 实验结果及分析
4.1 曲线特征提取结果及分析
真实数据为某酒厂白酒的发酵温度数据,每个样本有1440个数据,发酵过程中的温度是利用物联网无线测温技术在发酵过程中间隔1h测出的。在固态发酵的温度数据采集过程中,操作人员的失误操作、环境干扰和设备故障等会导致采集数据中含有小部分的野值。由于野值提供的信息不具有参考价值,反而会降低算法的性能,因此必须有效的剔除野值。高斯拟合对发酵温度数据的拟合效果非常好,可以用高斯拟合的方法消除野值,另外后面要对温度曲线进行特征提取,在误差允许的范围内,高斯拟合可以将随时间变化的温度点拟合成连续的曲线。
本文将发酵时间由小时转换为天数并用高斯拟合法对温度数据进行预处理,列举了白酒发酵过程的八个温度曲线图,横坐标单位是天(d),纵坐标是温度(℃),如图3(a)~(k)所示,然后对图3中的曲线图进行特征提取,选取了二叉树的前三层根节点,共七个特征,如表1所示。
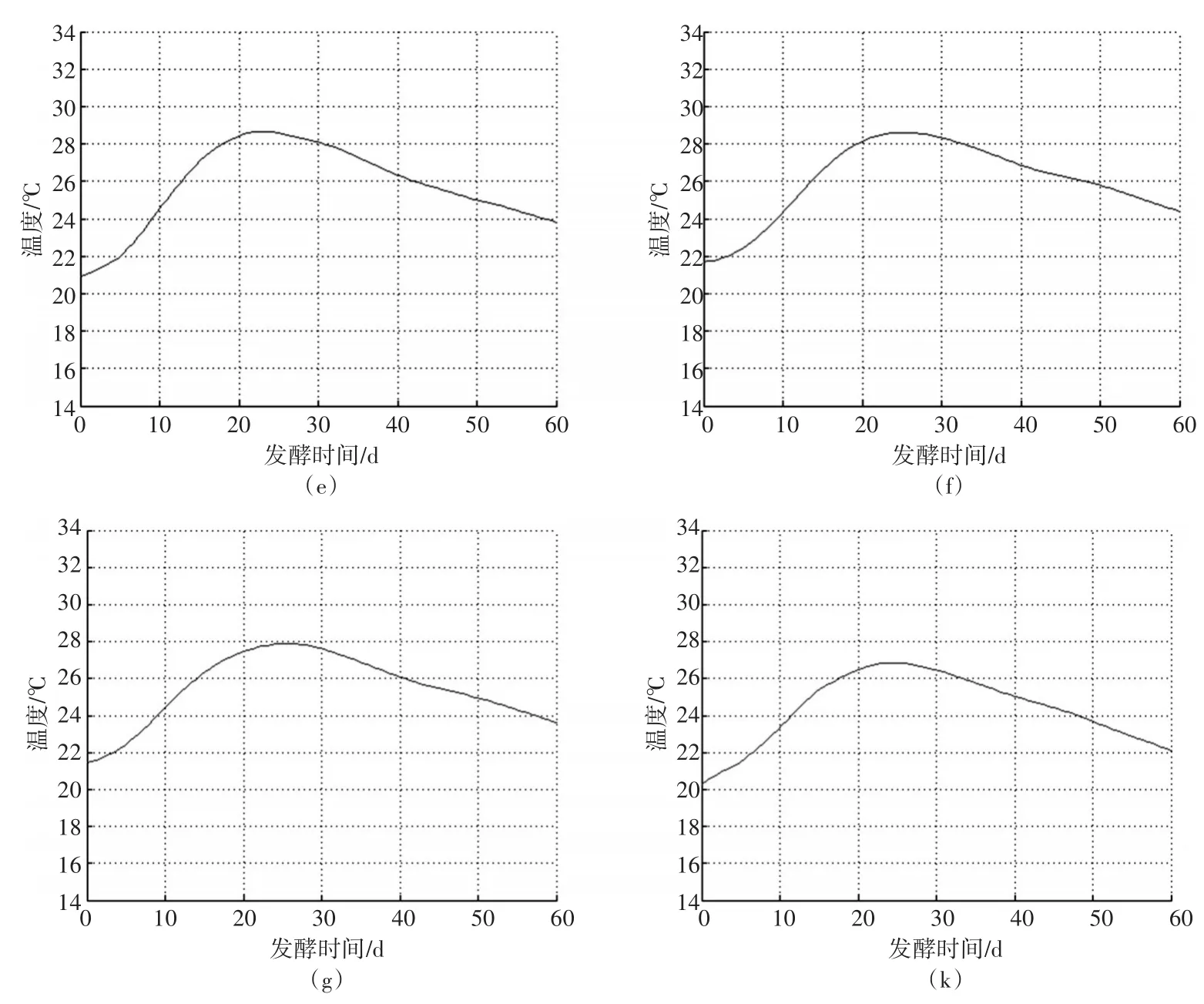
图3 白酒发酵过程的温度曲线图
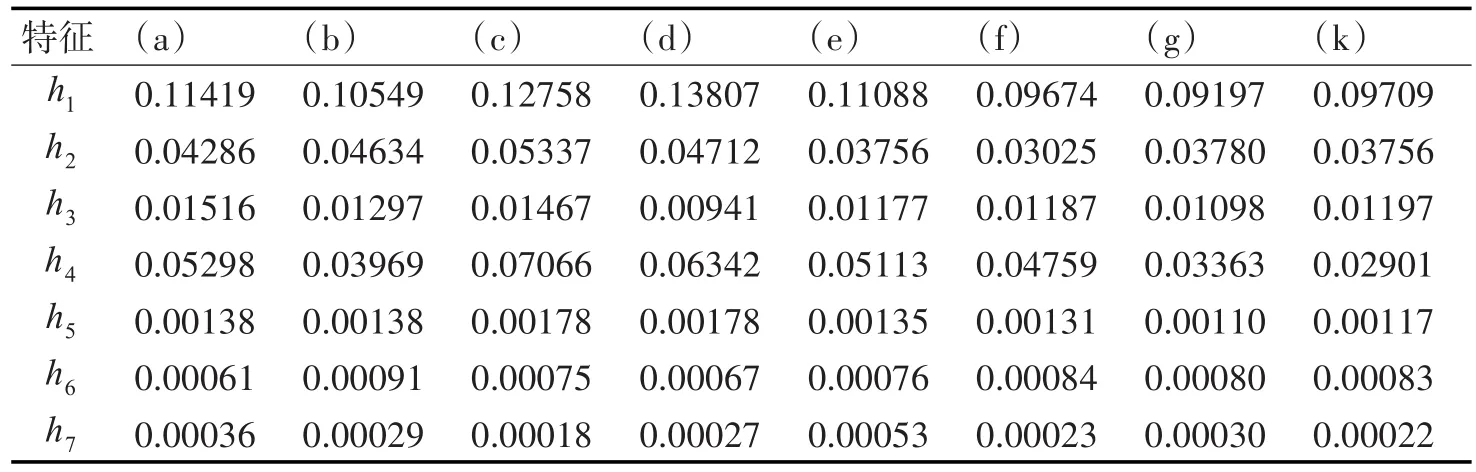
表1 图3中曲线对应的特征
由图3可以看出特征(a)和(b)、(c)和(d)、(e)和(f)、(g)和(k)的曲线图形状相似,但提取的特征依然可以准确地描述它们,由表1可知,它们在二叉树根节点上的相对高度大都不同,相似曲线的某些相对高度相近(如(e)和(f)、(g)和(k)),即使在某个根节点上相对高度相同(如(a)和(b)、(c)和(d)),但在其它根节点上则完全不同,一组特征只对应一个曲线,所以并不影响对两个相似曲线的描述,反而用特征表明了两个曲线是相似的,说明了曲线特征提取的准确性。又由表1可知,(a)~(k)相应的二叉树根节点下面的子节点存放的相对高度越来越小,这是因为曲线被多次划分,形成的曲线段越来越多,曲线段的弯曲程度也就越来越低,它们的相对高度就会更加趋近于零。
4.2 支持向量机分类结果及分析
实验所用配置:计算机配置为四核,内存(RAM)为4.00GB,CPU为1.5GHz,操作系统为Windows7 64位,算法用Matlab R2014a仿真。
本文用支持向量机对不同数目的样本集进行实验,支持向量机对高斯拟合法预处理后的温度数据分类,记为M1,支持向量机对提取出的温度曲线特征分类,记为M2,支持向量机对温度曲线特征、入窖水分、入窖酸度和入窖淀粉分类,记为M3,本次实验设置支持向量机参数为C=2,σ=1,训练样本数和测试样本数的比例均为1∶1,实验结果如表2所示。
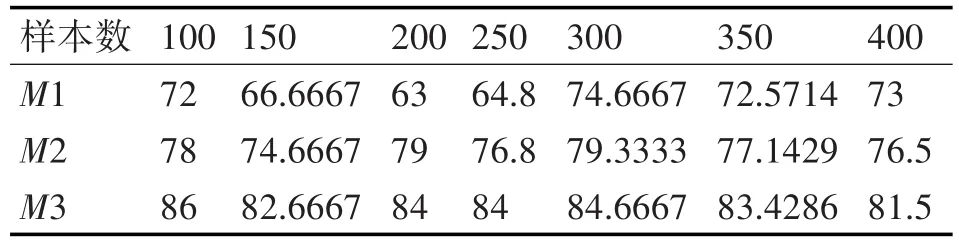
表2 三种方法在不同样本数上的分类正确率 %
由表2可知,对于不同样本数,M2的分类正确率均优于M1,在实际生产中,操作人员的经验是观察温度曲线的走势而不是用温度数据来判断产量高低,这里提取了发酵温度曲线的特征,用少量且唯一的特征描述了曲线的走势,分类准确率更好表明了特征提取的有效性,也说明了生产应用中操作人员的判断方式是正确的。M3的分类正确率均优于M2,这是因为M3的特征中加上了入窖水分、入窖酸度和入窖淀粉,充分考虑了影响白酒产量的因素,分类时用到的特征信息更全面。对于表2中的样本集,M3比M1平均提高了14.2225%,M3比M2平均提高了6.4027%。
5 结语
在白酒发酵过程中,发酵温度、入窖水分、入窖酸度和入窖淀粉是影响白酒出酒率的重要因素,对这些因素的研究是提高白酒出酒率的关键。本文采用支持向量机进行分类,由于温度数据维数过高导致入窖水分、入窖酸度和入窖淀粉的权重过低,本文引用相对高度的定义,借鉴其中的思想,提出了一种曲线特征提取算法,精确地提取温度曲线的特征,用相对高度刻画曲线的形状并存放在二叉树的根节点上,然后用支持向量机对曲线特征、入窖水分、入窖酸度和入窖淀粉进行分类(M3),与用支持向量机对温度数据分类(M1)和对提取的温度曲线特征分类(M2)相比,M3的分类效果明显好于M1和M2,分类准确率比M1和M2更高。根据发酵温度变化、入窖配料和分类结果,准备下一轮的入窖配料,从而进一步提高白酒的产量。

