三分量磁传感器的水平姿态校正方法∗

朱兴乐

（91336部队 秦皇岛 066000）

1 引言

三分量磁通门传感器在舰艇磁性检测及磁防护领域中有着广泛的应用［1～2］，因其操作简便，测量信息特征完整，常作为测量磁场的标准测量器件。三分量磁传感器内部以三个两两相互垂直的螺线管作为测量单元，构成了正交测量坐标系并可获得标准的三分量磁场信息。三分量磁传感器出厂时进行测试封装，即传感器内部三轴相互正交，内部敏感测量元件具有相同的标度系数且无零位偏移，在具体使用前首先调节传感器底座三个管脚以进行基座校准，保证传感器底盘水平且朝向满足要求［3～5］。由于工艺及人为调节的原因，传感器内部三轴会产生位移，进行水平调节仅保证了底座的水平，却并不能保证传感器内部三轴坐标系水平，从而导致磁测量值不能如实地反映外部磁场变化，将此因磁传感器内部不水平引起的误差称为水平误差。在移动式舰艇磁性检测站及水下磁传感器网络中，磁传感器一般采用万向平衡机构依靠重力自动调节水平，然而磁传感器内部测量元件的重心与几何中心并不完全一致，当传感器一旦放置后其不水平角度固定且难以调节，因此有必要在使用前补偿传感器的水平误差，以保证磁场测量的准确性。

针对三分量磁传感器的测量误差校正，一般对其本身固有误差研究较多，例如文献［6～7］对磁传感器的非正交误差提出了补偿方法，并采用最小二乘、共轭次梯度等算法进行校正，获得了良好的校正效果；文献［8～9］通过椭球拟合原理建立测量模型，对磁传感器的正交、零位、标度等磁传感器本身含有的误差进行了研究，可同时将三种误差一同校正。上述方法主要针对磁传感器的固有测量误差，而对其不水平放置时的姿态误差研究较少，文献［10］对水平误差进行了研究，采用共轭次梯度方法求解出磁传感器的水平误差系数。本文在此基础上对水平姿态误差模型进行了进一步研究，重新构造水平误差校正模型，并采用优化算法求解出磁传感器的校正矩阵系数，仿真证明了此方法的正确性，并在实验中对其进行验证，可将三分量磁传感器的测量误差有效补偿，提高了测量的精确度，改善了磁传感器的测量性能。

2 水平校正数学模型

设定三分量磁传感器测量前已进行固有误差校正，即测量时无非正交、标度及零位误差［11］，在此前提下磁传感器不水平问题可通过姿态变换进行解释。首先建立磁传感器的非水平测量模型，以磁传感器中心点为原点，理想正交坐标系表示为oxyz，对其进行姿态旋转可得到磁传感器的非水平坐标系，具体步骤及示意图如图1所示。

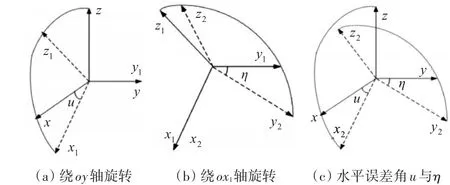
图1 水平误差角定义

1）正交水平坐标系为oxyz，以oy为轴旋转成坐标系ox1y1z1，ox1与ox成u角，如图1（a）所示。

2）在坐标系ox1y1z1内以ox1为轴旋转成坐标系ox2y2z2，oy2与 oy1成η角，如图1（b）所示。

3）ox2y2z2为磁传感器坐标系，其中ox2在 oxz平面内，oy在oy2z2平面内，u与η称之为水平误差角。

在正交水平坐标系下磁测量值为B，则在步骤1）中坐标系ox1y1z1测量值为B1，两者关系可表达为

经步骤2）中变换在坐标系ox2y2z2下测量值为B2，B2为三分量磁传感器非水平状态下的磁场测量值，推导可知B1与B2关系为

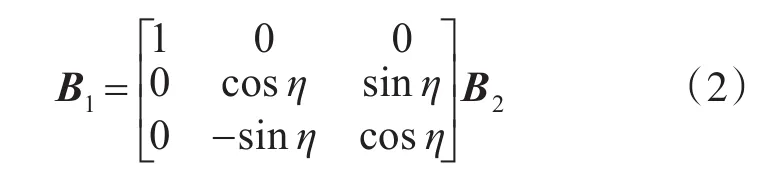
对上式进行矩阵变换，可得非水平测量值B2与理想正交测量值B间的表达式：

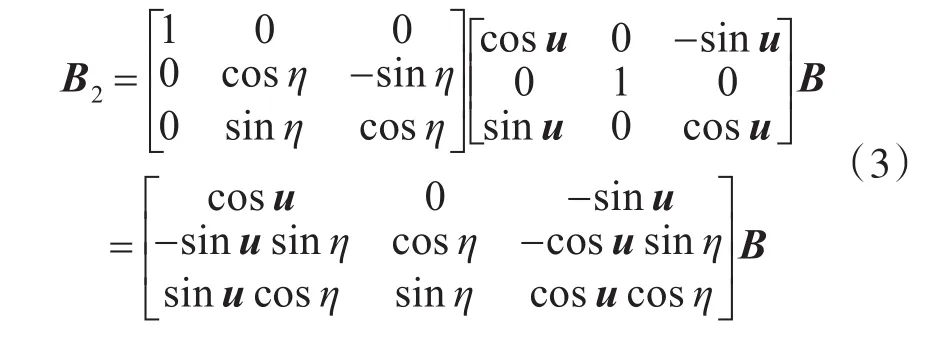
上式的简化形式表达为B2=HB，H称为水平误差校正矩阵。对矩阵H分析可知H为正交矩阵（HHT=E），其模值与水平误差角u与η不相关，当u与η变化时，H模值始终为1，说明磁传感器的非水平状态只改变了磁场总量在三分量上的分布，总强度未发生改变，即磁传感器无软磁及硬磁偏移，这也从侧面说明此情况下磁传感器无固有测量误差。当三分量磁传感器处于理想水平状态时，以垂直方向（Z轴）旋转，其磁场测量值的Z分量应保持不变，X与Y分量应随转动角度呈正余弦关系变化，其水平方向上的总量应稳定不变，因此在对磁传感器进行水平校正时，可将此特性作为求解约束条件，以求解出水平姿态角，进而获得准确的磁场测量值。

磁传感器在倾斜姿态下含有不水平误差，转动磁传感器所在位置的旋转托盘并进行测量，共获得n个三分量测量数据Bm，Bm与水平误差角u、η角的函数关系为

根据上式建立磁传感器的校正模型，采用优化算法进行误差校正后得到校正值Bc，由上述分析可知磁传感器校正值的Z分量应为一致，由此可建校正模型的目标函数：

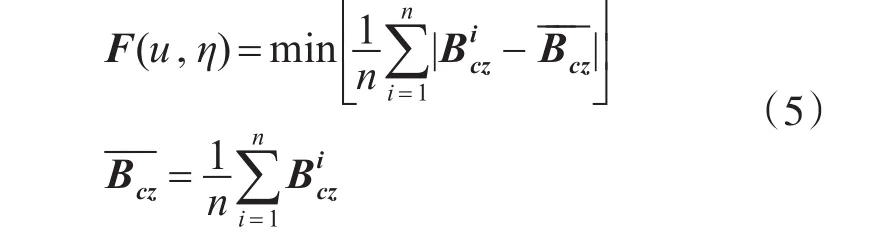
其中Bicz为校正后磁场测量数据Z分量的第i个数值，为校正数据的总体平均值，上式表明当校正后磁测量数据Z分量整体一致或变化幅度趋近于0时，可获得较准确的水平误差角数值，并由此对误差进行较好的补偿。

3 求解方法

针对磁传感器的误差校正，可采用最小二乘、牛顿优化、椭球拟合校正等方法进行求解，鉴于微分进化算法（Differential Evolution algorithm，DE）在求解速度及收敛性上的优越性，采用DE算法对磁传感器的水平误差角进行求解，其主要具体步骤如下［13］：

1）初始化。设定种群中个体数量为N，第i个个体向量为Xi=［xi1，xi2］，其中个体中元素为水平误差角，即xi1代表u，xi2代表η，所在搜索空间范围［xmin，xmax］，则初始化公式为

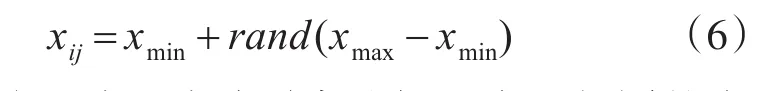
2）变异。随机从种群中选择三个不相同的个体，将其中两个进行差分加权后，通过下式与第三个个体求和以获得变异个体［10］：

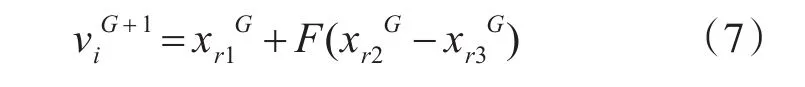
G代表迭代次数；F为缩放因子，F∈［0，2］，用于控制差分矢量对变异个体的影响。

3）交叉。交叉操作采用二项分布得到新的试验个体uiG+1：

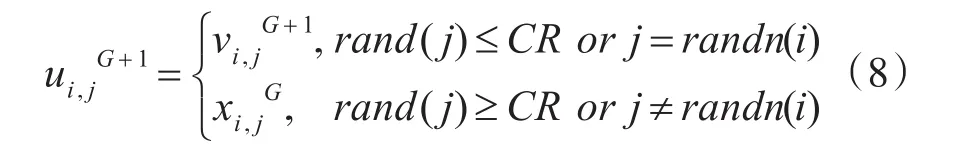
CR为交叉概率，CR越大有利于局部搜索，CR越小有利于种群多样性。rand（j）为0～1间均匀分布的随机数，randn（i）为1～D 中随机整数。

4）选择。DE采用贪婪搜索原理，将uiG+1与xiG进行竞争，当uiG+1的适应度值大于xiG时才被选为子代，否则将采用xiG作为子代。

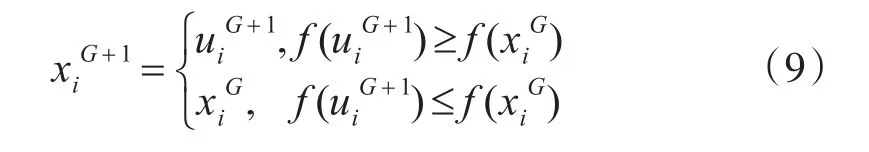
4 实验结果及分析

4.1 仿真及分析

为表明磁传感器不水平对磁测量数据的影响，对此状态下的磁场测量数据进行了仿真。设定地磁总强度为50000nT，磁偏角D=50°，磁倾角I=35°，则可获得理想条件下正交磁传感器的测量值。设定非水平磁传感器的水平误差角分别为u=3°，η=5°，以Z方向为轴等角度均匀转动磁传感器所在水平底盘，共获得40组测量数据。采用误差圆的方法对理想正交及非水平状态下的测量数据进行对比，其原理是若磁传感器绝对水平，则其测量值在X-Y平面应为标准圆，非水平将导致标准圆发生倾斜形变，以此直观显示磁传感器不水平对磁测量的作用，同时计算两种情形下磁测量数据间的差值ΔB，其结果如图2所示。

图2 对比结果

上述结果显示磁传感器非水平对磁测量产生了较大影响，图2（a）中误差圆距标准圆产生较大偏移，磁测量值在三分量上的偏差达到上千纳特，因此有必要对磁传感器的非水平误差进行补偿。采用DE算法对此条件下的磁测量数据进行校正，其中算法中初始参数设定如下：

1）种群中个体数量N=50，每个个体中含有两个元素，分别代表u与η，两者的搜索空间均为［-20°，20°］。

2）缩放因子F=0.5，交叉概率CR=0.9，迭代次数G=100。

由式（4）建立适应度函数，根据适应度值大小选择最优个体。迭代计算水平误差角，具体结果如图3所示。

上述结果显示水平校正后求解的水平误差角与设定值一致，且磁测量数据校正值的Z分量Bcz为稳定值，说明此方法正确有效，磁传感器的水平误差已有效补偿。

4.2 实验验证

对实际中磁传感器的不水平问题进行验证。在地磁场背景下将磁传感器安放于可水平旋转的底座上，调整不水平角度并以20°等角度旋转底座，共测得30组测量数据Bm。采用上述方法对其进行校正，其结果如图4及表1所示。

图3 求解结果

图4 求解结果

由上述结果可知，经多次迭代求解后目标函数值降到最低，水平误差角度得出最优值，求解结果为u=0.31279，η=-0.09315，将其代入式（2）对测量数据进行反推，可得水平校正后磁测量值Bc，对比校正前后磁测量值的Z分量，MSE为测量数据均方差，具体结果如表1所示。

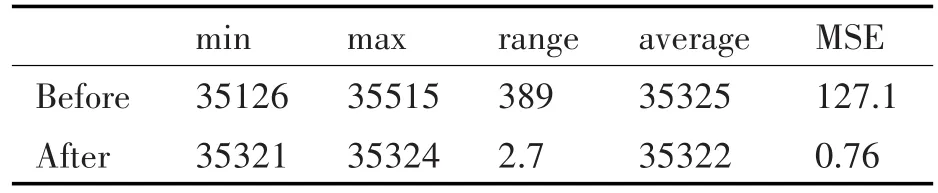
表1 求解结果

由表1可知经过水平误差校正后Bcz波动幅度由校正前近400nT降到小于5nT，说明将磁传感器坐标系不水平引起的测量误差有效消除，获得了较准确的磁测量数据。

5 结语

三分量磁通门传感器的水平测量误差是在磁场测量中的重要问题。在磁传感器无固有测量误差的前提下进行了水平误差的研究，构建了磁传感器的不水平测量模型，采用优化算法进行了水平误差角度的求解，实验表明该方法将磁传感器的误差降到10nT以下，对磁传感器的水平误差进行了有效补偿，提高了测量的准确度，解决了三分量磁传感器的不水平测量问题。