基于长短记忆网络的舰船航迹预测方法∗

杨金鸿 皇甫立 熊 璋 许 松 王新远

（1.中国船舶工业系统工程研究院 北京 100094）（2.北京航空航天大学 北京 100191）

1 引言

舰船航迹预测在舰船航行跟踪、防止撞击、事故预警、调度分配、航行决策支持、海洋交通管制等各方面发挥着重要作用［1］。目前针对舰船航迹预测的方法主要包括：基于数学方程的方法、基于灰色系统的方法和基于马尔科夫的方法［2］。传统基于数学方程的航迹预测主要采用卡尔曼滤波［3］、粒子滤波等方法［4］，这些方法通过建立运动学［5～6］或动力学［7］数学方程刻画舰船运动过程。在理想的环境下，这些数学方程能够精准地计算舰船运动航迹。然而，众所周知，海洋环境复杂多变，海风、海况、水流等诸多环境因素对舰船运动影响较大。并且诸多干扰因素之间相互影响、互相干扰，进一步加剧了舰船运动的复杂性。传统的数学方程难以考虑海风、海况、水流等诸多环境因素的影响。基于灰色系统的方法通过分析系统因素间的关联关系，建立相应的微分方程模型，从而预测事物未来发展趋势的状况［8］。目前使用最广泛的灰色预测模型是关于数列预测的单变量、一阶微分GM（1，1）模型。GM（1，1）模型的基本假设是：将系统原始时间序列按时间维度进行累加，累加后的时间序列呈现的规律可用一阶线性微分方程的解来逼近。经理论研究，由一阶线性微分方程逼近拟合的原始时间序列呈指数变化规律。因此，当原始时间序列隐含着指数变化规律时，灰色模型GM（1，1）的预测是非常有效的。基于马尔科夫链的预测方法将航迹预测问题转化为状态转移问题，根据历史数据求解状态转移概率矩阵，依据当前状态预测下一时刻的状态。

随着人工智能技术的迅速发展，智能技术成为解决不确定问题的重要途径，在解决诸多实际问题中发挥着重要作用［9］。在基于神经网络的航迹预测方面，徐婷婷提出基于BP神经网络的舰船航迹实时预测方法［10］，该方法建立输入层、隐藏层和输出层三层神经网络结构，以航向、航速为输入，预测下一个时间周期的经度差、纬度差。然而BP神经网络的方法仅仅利用当前时刻的航向、航速预测下一时刻的偏移量，而无法利用任何短期历史信息。

近年来提出的深度学习方法是一种具备多层感知的深度网络模型，具有强大的非线性处理能力和良好的“记忆”性质［11］。长短记忆网络作为一种经典的深度学习算法，能够较好地刻画时间序列系统内部发展规律，预测时间序列系统发展趋势［12］。目前LSTM已广泛应用于语音识别、翻译、时间序列预测等领域。舰船航迹具有明显的平滑性，下一时刻的位置状态由历史时刻的位置滑行而来。可见，利用舰船历史时刻位置预测下一时刻的位置状态，将有利于提高航迹预测的精度。在复杂的海洋环境中，在一定时间内海况信息是类似的，下一时刻的船舶运动状态不仅与当前时刻有关，而且与历史时刻也有关。LSTM是一种时间序列预测方法，与基于BP神经的预测方法相比，基于LSTM的方法能够预测更长的周期。文献［11］提出基于循环神经网的轨迹预测方法，对用户出行的轨迹地点进行预测。但是该方法主要针对商厦、学校、地铁站、公司、加油站等离散的轨迹位置状态进行预测。舰船航迹分布于连续时间空间中，具有明显的时空连续性，如何对时空连续航迹进行预测需要进一步研究。本文首先提出连续位置向量化方法，构建长短记忆网络模型，提出基于滑动窗口的LSTM航迹预测算法，利用历史航迹数据训练LSTM模型，采用滑动窗口的方法预测未来时间周期数据。实验仿真三种典型的舰船机动场景，结果验证了本文所提方法的有效性。

2 基于长短记忆网络的舰船航迹预测算法

2.1 LSTM航迹预测模型

LSTM作为一种经典的循环神经网络，将上一个时间周期的输出作为下一个时间周期的输入，如图1所示为按时间展开的循环神经网络模型。LSTM单元主要由输入门、输出门、遗忘门和输入节点等组成，LSTM的记忆细胞结构如图2所示。

图1 LSTM网络概略图

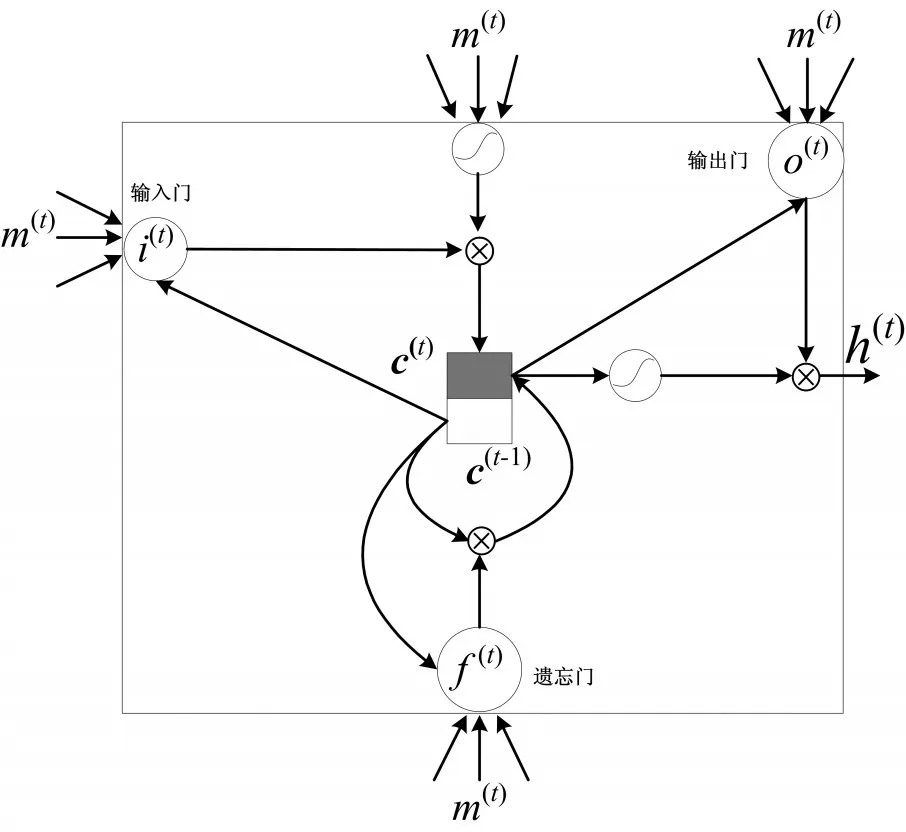
图2 长短期记忆神经网络记忆细胞结构

其中c为记忆单元，i为输入门，o为输出门，f为遗忘门，o为记忆单元输出，t表示时间周期。假设输入向量m(t)=(θ(t)，v(t))表示第t个时间周期的输入向量的集合，h（t）表示第t个时间周期的隐藏层状态，i（t）表示第 t个时间周期的输入门的输出状态，f（t）表示第t个时间周期遗忘门的输出状态，o（t）表示第t个时间周期输出门的输出状态，c（t）表示第 t个时间周期记忆门的输出状态，那么其定义可分别表示为

其中，σ是sigmoid函数。b表示偏置量。W表示权重向量，利用权值矩阵的下标表示矩阵具体含义，例如Whi代表的就是隐藏层与输入门的权值矩阵。在此基础上，可通过式（1）～（5）计算并更新LSTM单元在每一时刻的状态。

在复杂的海洋环境中，不同时刻船舶运动状态之间存在复杂的非线性关系，利用神经网络拟合历史时刻运动状态与下一时刻船舶运动状态之间的关系。在基于LSTM模型的预测中，将船舶航行的历史运动状态输入模型中，预测下一个时间周期船舶运动状态。已知探测到舰船在1至T时刻的运动状态信息，根据时间上的有序形式组成的运动状态序列集合称为M（Motion Elements）。

定义1（运动状态序列集）对船舶的运动状态建模，利用每个时间舰船航行方向和速度组成运动状态序列：

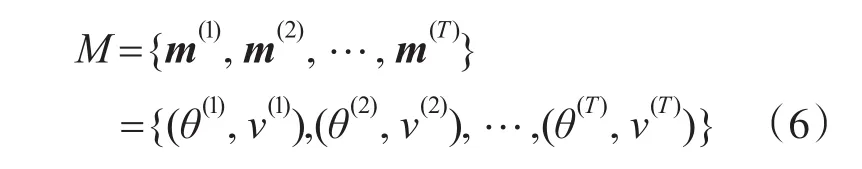
其中 θ(t)（1≤t≤T ，0≤θ(t)≤2π）表示船舶在t时刻的航向与Y轴的夹角，v(t)表示舰船在t时刻的航行速度，称M为运动状态序列集。

每个神经元由两个输入端、两个输出端组成；m(t)=(θ(t)，v(t))是模型的输入，o(t)=((t)，(t))为模型的输出。连续的航迹预测分为若干离散时间周期，为了预测多个时间周期的运动航迹，定义每个时间周期的船位差序列集如下：

定义2（船位差序列集）对舰船的船位差进行建模，利用X与Y两个方向上的矢量表示船位差：

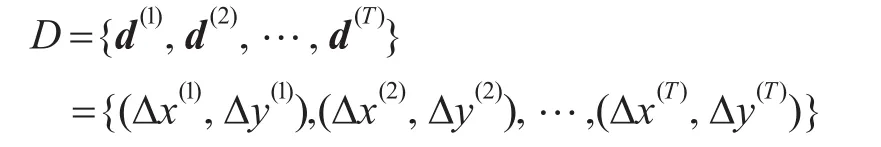
其中Δx(t)（1≤t≤T）表示舰船在时间周期t时刻的在X轴的船位差的投影，Δy(t)（1≤t≤T）表示舰船在时间周期t时刻的在Y轴的船位差的投影。Δx和Δy分别表示舰船运动的横坐标船位差和纵坐标船位差。根据模型的输出o（t）计算每个时间周期的船位差如下：

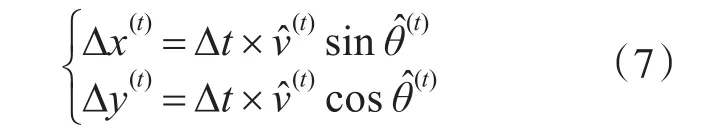
根据船位差序列预测t时刻船舶的位置如下：

2.2 基于滑动窗口的LSTM航迹预测模型

为了对更长的时间周期进行预测，提出基于滑动窗口的LSTM预测模型。假设可以得到的实时观测运动状态序列个数为T，选取长度为N的滑窗。以滑窗的长度限制输入训练序列的长度，避免迭代过程中学习时间过长。为了进行中长期预测，可以采用迭代法对滑窗中的样本进行更新。假设需要预测l步航迹，则通过每次迭代，对第i（i=1，2，3，…，l）步的预测值替换滑窗中最旧的数据，每替换一次便让LSTM网络进行一次新的学习，更新网络结构，以新的网络结构进行下一步的预测。滑窗样本替换方法如图3所示。

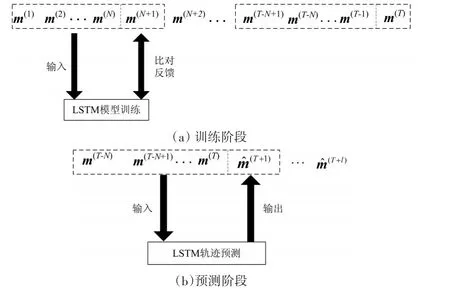
图3 基于滑动窗口的LSTM模型

在训练阶段：将探测到的历史数据进行分组，每组N+1个数据，前N个数据作为输入数据，预测第N+1个数据值，与第N+1个数据的真实值做对比误差，迭代调整网络参数，如图3（a）。

在预测阶段：利用探测到的第T-N至T个数据预测未来第T+1时刻的数据，再由T-N+1至T+1个数据预测第T+2个数据，直至预测未来l个数据，如图 3（b）。

3 仿真验证

为了验证本文所提方法的有效性，选取三种典型的航行应用场景，分别是左满舵、右满舵和S型航线航行。本实验将前70%时间周期作为训练样本，预测后30%时间周期的航迹。通过与真实航迹对比，分析LSTM方法和灰色系统模型GM（1，1）的预测效果。

定义3（预测均方误差）对于预测轨迹点与实际轨迹点的几何空间误差采用式（5）所示的均方根误差RMSE来计算：

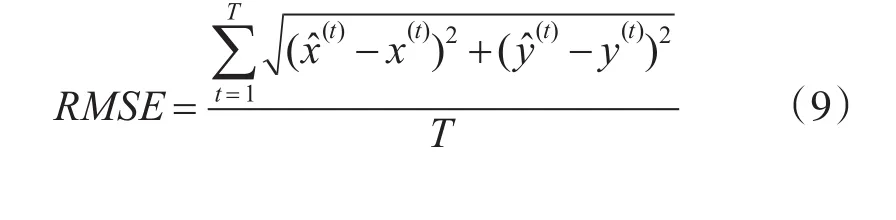
其中，（ x(t)，y(t)）表示实际轨迹点的位置，（(t)，(t)）表示预测轨迹点的位置信息，T表示预测轨迹点的时间周期数量。

如图4所示为真实航迹以及灰色系统和LSTM的航迹预测结果。结果表明，与灰色系统预测方法相比，LSTM预测结果更接近于真实航迹。图5所示为每个时间周期灰色系统和LSTM预测位置的距离误差，总体结果表明LSTM的预测误差明显低于灰色系统方法。图6所示为灰色系统和LSTM预测的均方误差，对比分析结果表明LSTM的预测精度优于灰色系统方法，原因是LSTM具有较强的记忆能力，能够记忆历史时刻航迹位置，推断航迹变化趋势，具有较好的预测能力。长短期记忆神经网络采用一个特定的记忆细胞存储信息，对于存在依赖关系的历史信息有着非常重要的作用。通过引入输入门、输出门和遗忘门，LSTM有效提高了面对具有长时依赖性时序数据的学习、分析能力，所以LSTM对于处理变长序列的效果是非常好的。

图4 航迹预测结果对比

图5 预测距离误差

图6 均方误差对比

4 结语

采用LSTM来解决舰船的轨迹预测问题。研究结果表明，针对舰船不同的航行场景，提出的方法在预测精度方面均高于灰色系统预测方法。可见依靠LSTM解决舰船的轨迹预测具有很好的应用前景。下一步考虑将舰船运动方程融入到LSTM模型中，进一步提高LSTM的舰船航迹预测精度。