基于混合车型的灵活型接驳公交路径协同优化研究

邵文，贾顺平，曹文娟

(北京交通大学交通运输学院，北京 100044)

目前，我国城市公共交通系统以轨道交通为骨干，常规公交为主体，由于二者“定点”与“定线”的特性，乘客出行需要一定距离的绕行，无法满足非高峰时段居民出行需求。相比固定线路公交，灵活型接驳公交作为介于常规公交与出租车之间的新兴公交服务模式，具有更优的机动性、便捷性和舒适性，可提高居民出行直达性，是完善城市交通资源优化配置的有效方法。该系统多适用于城市边缘地带、高科技园区、新型居民区等客流密度中等偏低的地区，是联系周边交通小区与主线公交的纽带，其调度方案和停靠站位置可根据乘客需求调整，能有效满足低出行密度区域多样化、个性化的居民出行需求。

国外关于灵活型接驳公交系统的研究要早于国内，有较为充分的理论成果并得以应用。Cole[1]提出的7种交通运营模式之一的Dial-a-Bus系统作为灵活型接驳公交系统的雏形，旨在解决低密度人口区域居民出行难的问题。Flussberg[2]提出了根据乘客出行需求在特定区域提供灵活型接驳服务的Merrill-Go-Round系统，并进行了实例应用研究。现有的针对灵活型接驳公交线路调度优化的研究多是关于可变线路式的服务系统(mobility allowance shuttle transit，MAST)，即车辆围绕一条由若干站点组成的基准线路运行，车辆可在两固定站点间允许的松弛时间内一定程度地偏离基准线路。针对MAST系统的线路设计、车辆调度等优化问题，Malucelli等[3]建立了离线优化模型，Quadrifoglio等[4-5]建立了混合整数规划模型，并提出插入式启发算法求解[6-7]，但均未充分考虑接驳公交与主线公交时刻表的协同优化。国内学者对于该系统的研究起步较晚，但也取得了一些研究成果。熊杰等[8]综合考虑路径出行时间和圈点线路约束，以路径需求潜力最大化为优化目标，建立地铁接驳线路的路径优化模型，并提出基于路段交叉变异的遗传算法求解模型。潘述亮等[9]兼顾出行者和运营者双方利益，就接驳系统线路规划和车辆协同问题，建立路径优化和协调调度整数规划模型，并设计了一种基于新型重模型的启发式算法进行求解。刘心雨等[10]研究了保障乘客在期望时间及可接受延误时间范围内到达换乘中心的前提下，基于乘客不同出行目的的接驳公交线路调度优化方案。目前，国内外关于灵活型接驳公交服务系统的研究多侧重于减少系统出行成本，而忽略了公交服务满意度这一关键因素。将公交服务满意度纳入系统优化目标将有助于提高公交服务水平，增强客流吸引力[11]。

本文考虑乘客满意度这一影响因素，将其转化为接驳公交与主线公交时刻表的协同优化，兼顾混合车型对灵活型公交接驳系统运营成本的影响，针对灵活型接驳公交的路径优化及协同调度问题展开研究。以单个换乘站点为研究对象，同一个固定换乘点作为接驳公交的起讫点，依据乘客预约出行需求和各需求点车辆到达时间动态优化接驳车辆的运行线路和调度方案，最终生成多条车辆行驶路径，即在给定预约需求和车队规模的前提下，以最大化乘客满意度和最小化企业运营成本为优化目标，建立基于混合车型的灵活型接驳公交路径协同优化模型，并使用遗传算法对该模型进行求解。

1 研究问题描述

本文所研究的灵活型接驳公交可定义为依托于互联网平台，运营方根据乘客预约的出行申请设计车辆行驶线路，完成招募乘客、预订座位、在线支付等一系列公交服务[12]。

为研究车辆路径优化问题，现进行详细描述：在服务区域内有1个固定换乘站点和n个需求点，换乘点内有mp辆不同类型容量为Qp的接驳车辆供其调配，输出结果为多条车辆行驶的有向路径。以车辆把乘客从需求点送达换乘站的过程为例，车辆一次接驳服务可定义为：车辆从换乘站点出发，基于乘客预约的确定性需求依次对需求响应站点服务后，最终返回原换乘站点，即完成“多对一”条件下的接驳车辆路径优化和调度方案设计。如图1所示，图中有3条接驳线路，线路1采用车型a服务，线路2和线路3均采用车型b服务。

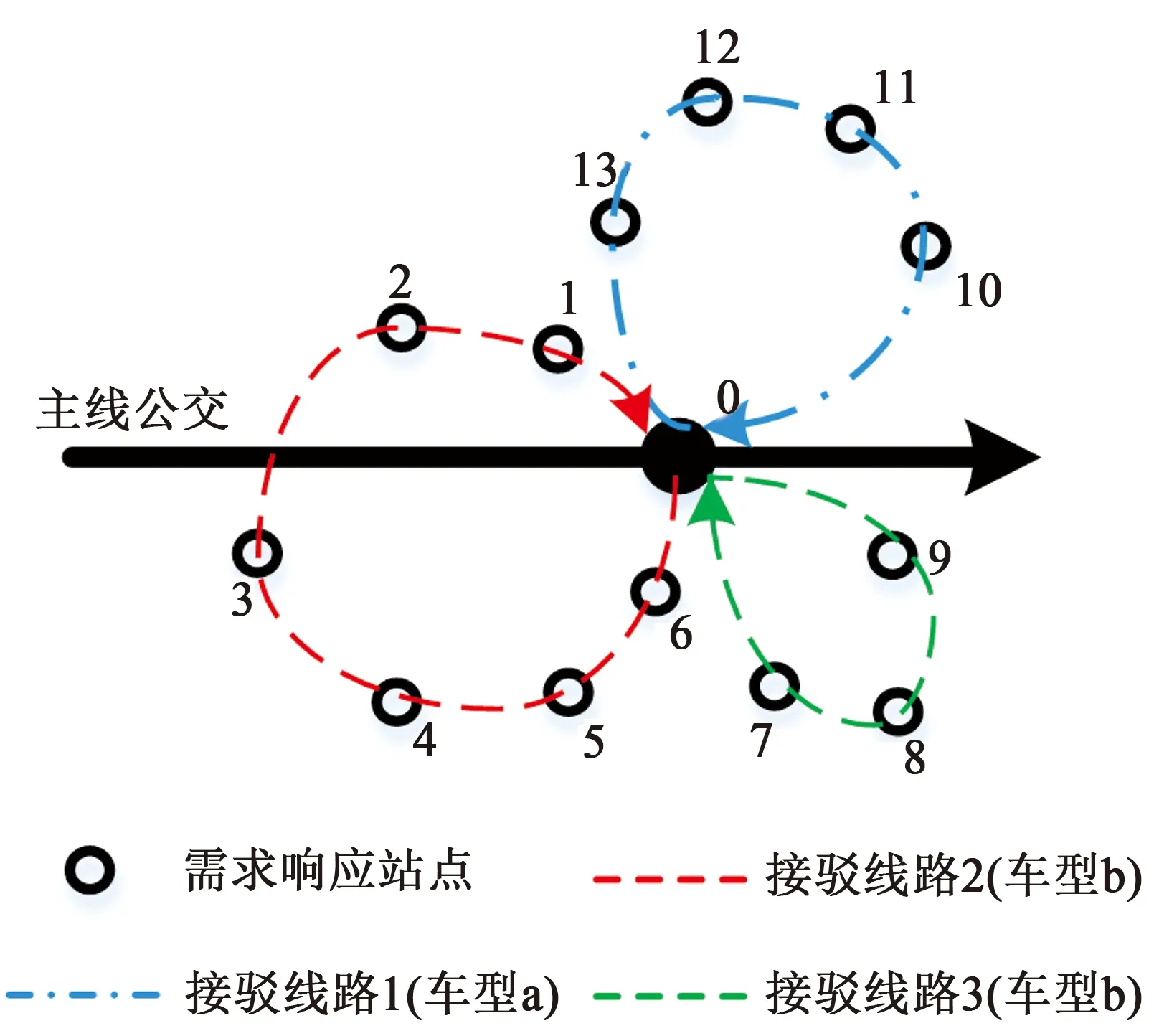
图1 基于混合车型的接驳车辆行驶路线示意图Fig.1 Schematic of the flexible shuttle transit routing based on various vehicle types

2 灵活型接驳公交路径协同优化模型

2.1 模型假设

定义编号0为换乘站，编号1,2,3,…,n为乘客需求点。在建模过程中，进行如下假设：

(1)服务区域内有1个换乘站点和n个需求响应站点，各站点位置已知；

(2)接驳车辆保持一定的速度在各站点间匀速行驶，忽略特殊交通状况和乘客上下车对车速的影响，不考虑延时和等待；

(3)换乘站点和各需求点间均互相通达，每两个站点间的行程时间固定且已知；

(4)换乘站所能提供接驳服务的车队规模已知；

(5)服务区域内不存在拒绝服务乘客的情况，所有有预约申请的乘客均被服务；

(6)乘客提交预约申请时，明确出行需求，包括需求点位置、出发时刻、期望和可容忍服务时间窗，只能将换乘点和需求点作为出行起讫点，起讫点不能均是需求点；

(7)接驳公交系统只服务于有预约申请的乘客，所有申请均在车辆出发前完成，行驶过程中不存在乘客需求变动的情况。

2.2 模型构建

模型中的主要参数和决策变量的含义如表1所示。

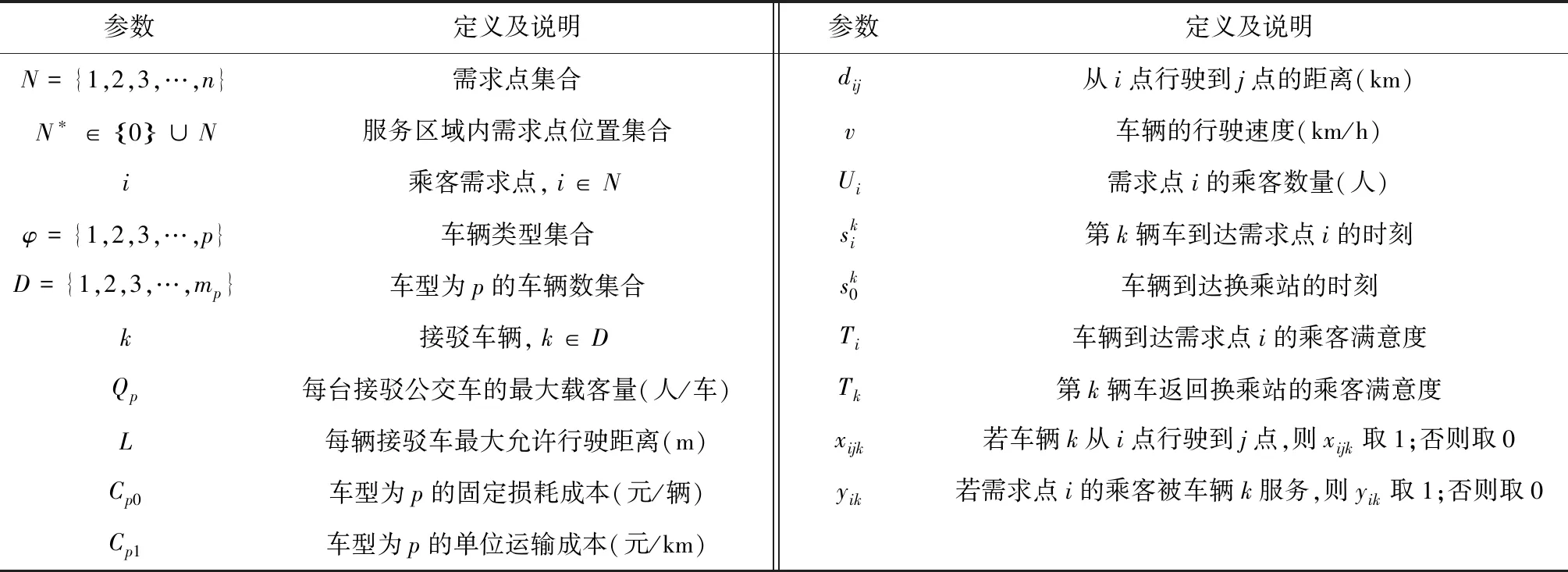
表1 模型参数

2.2.1 目标函数

灵活型接驳公交属于城市公共交通的类别，其运营一般需要兼顾乘客和企业双方利益，在保证乘客满意度水平的同时降低企业运营成本。基于此，本文将以企业运营成本最小和乘客满意度最大两部分作为目标函数建立模型。

(1)最小化企业运营成本

参考已有研究，公交企业运营成本主要包括车辆损耗成本和车辆油耗成本[13]。车辆损耗成本为每次启动车辆时所产生的折旧损耗费用，与发车次数相关；车辆油耗成本与车辆类型和行驶里程有关，不同类型车辆的油耗成本与行驶里程成正比例关系。

所以公交企业运营成本可表示为：

(1)

(2)最大化乘客满意度

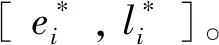
(2)

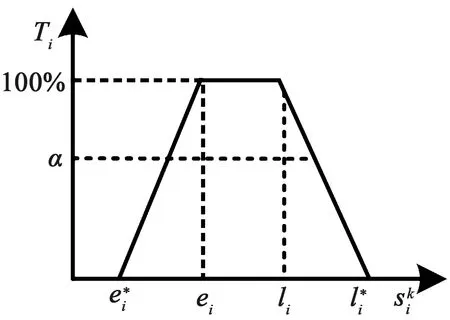
图2 软时间窗约束下乘客满意度函数图Fig.2 Passenger satisfaction function with soft time window constraints

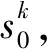
(3)

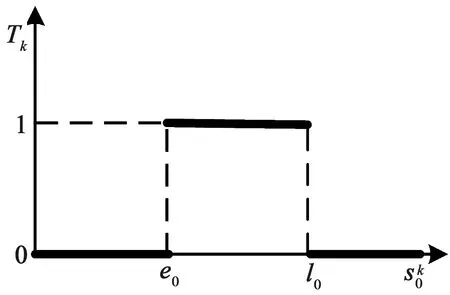
图3 硬时间窗约束下乘客满意度函数图Fig.3 Passenger satisfaction function with hard time window constraints

因此，乘客满意度函数可整理如公式4所示，乘客满意度最大的目标函数如公式5所示。

(4)

maxZ2=fsat。

(5)

2.2.2 模型综合表述

s.t.

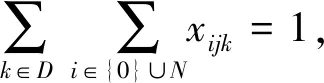
(6)

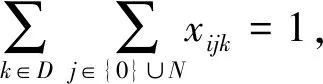
(7)

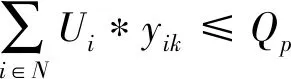
(8)

(9)

,∀k∈D，

(10)

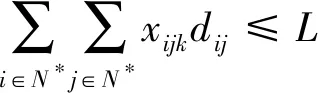
(11)

(12)

(13)

(14)

(15)

式(6)、(7)表示接驳车辆行驶过程中各需求点仅有1条行驶路径；式(8)表示车上乘客数不超过p车型的额定载客量；式(9)表示调度过程中所使用的各车型车辆数不可超出换乘站总配备车辆数；式(10)表示车辆从换乘站点出发，最终返回原换乘站完成接驳服务；式(11)表示一次接驳服务行程中，每辆车不得超过最大允许行驶距离；式(12)表示需求点i乘客满意度函数的软时间窗约束；式(13)表示第k辆车返回换乘站的乘客满意度函数的硬时间窗约束；式(14)、(15)表示接驳车辆到达需求点i的时间约束。

3 模型求解

本文研究的基于混合车型的灵活型接驳公交路径协同优化模型带有乘客满意度的时间窗约束，属于典型的带有时间窗约束的开放式车辆路径问题(vehicle routing problem，VRP)。车辆路径问题的求解方法可分为精确算法和启发式算法，精确算法包括分支定界法和列生成法等，启发式算法包括蚁群算法、模拟退火算法和遗传算法等。

蚁群算法是一种基于种群的进化算法，具有很强的发现较好解的能力和鲁棒性，易于与多种启发式算法结合，在解决一些小规模的旅行商问题(travelling salesman problem，TSP)时表现较好，但随着问题规模的增大，难以在可接受的循环次数内找到最优解。模拟退火算法能够以较大概率求得较优解，具有较强的鲁棒性、全局收敛性以及隐含并行性，通用性强，易于实现，但是该算法缺乏历史搜索信息，每次能保留一个解，对整个搜索空间的搜索能力不强。遗传算法提供了一种求解非线性、多模型、多目标等复杂系统优化问题的通用框架，具有较强的全局搜索能力和隐含并行搜索特性，按照一定概率的变迁规则来指导搜索方向，具有较强的自组织和自适应的能力，是一种实用、高效、鲁棒性强的优化技术。因此，本文利用遗传算法求解该路径优化模型。

3.1 染色体编码及种群初始化

本文采用自然数编码策略求解车辆调度模型，将染色体编码成长度为n+k+1的个体，1，2，3，…，n为各需求点的编号，n+1～n+k为k辆接驳公交的编号。由于需求点位置在车辆出发前已确定，对车辆进行编码，0代表不使用，1代表使用。个体向量的第1个分量代表第1辆车服务的第1个乘客，接着寻找满足时间窗和车容量约束的乘客加入到当前路径中，直至不满足约束条件时停止，最终得到该车辆的行驶路径。例如，若确定车辆1、4、7投入使用，基于车辆编码结果确定乘客编码，对于乘客1随机生成1～3的数字。若输出数字2，表示车辆4对乘客1进行服务。

本文采取随机排列策略生成初始种群，以保证种群多样性的最大化，将所有乘客的出行需求随机排列，形成初始个体向量并设置种群规模。

3.2 适应度函数

3.2.1 统一求解方向

该模型的优化目标包括最小化企业运营成本和最大化乘客满意度两部分，属于是多目标问题优化，由于目标函数求解方向不同，需要统一求解方向，将乘客满意度极大值转换为不满意度极小值进行求解。

minZ3=min(1-fsat)。

(16)

3.2.2 归一化处理

因企业运营成本和乘客满意度量纲不同，且乘客满意度取值范围为0～1，需对运营成本进行归一化处理，处理结果为：

G*=Gm/Gmax，

(17)

H*=Hm/Hmax，

(18)

其中，G*和H*分别表示未归一化后的车辆损耗成本和油耗成本，Gm和Hm分别表示个体cm中实际的损耗成本和油耗成本，Gmax和Hmax分别表示当前种群个体中的损耗成本和油耗成本的最大值。

3.2.3 多目标函数处理

为将多目标优化模型转变为单目标优化问题，可将目标函数变为求企业运营成本和平均乘客不满意度之和的最小值。本文依据运营成本和乘客满意度对系统的影响程度赋予不同的权重值，并且取两者之和的倒数，构造适应度函数如式(19)所示。个体适应度函数值越大，表明其适应度越强。

g(cm)=1/[w1G*+w2H*+w3(1-fsat)]。

(20)

3.2.4 遗传操作

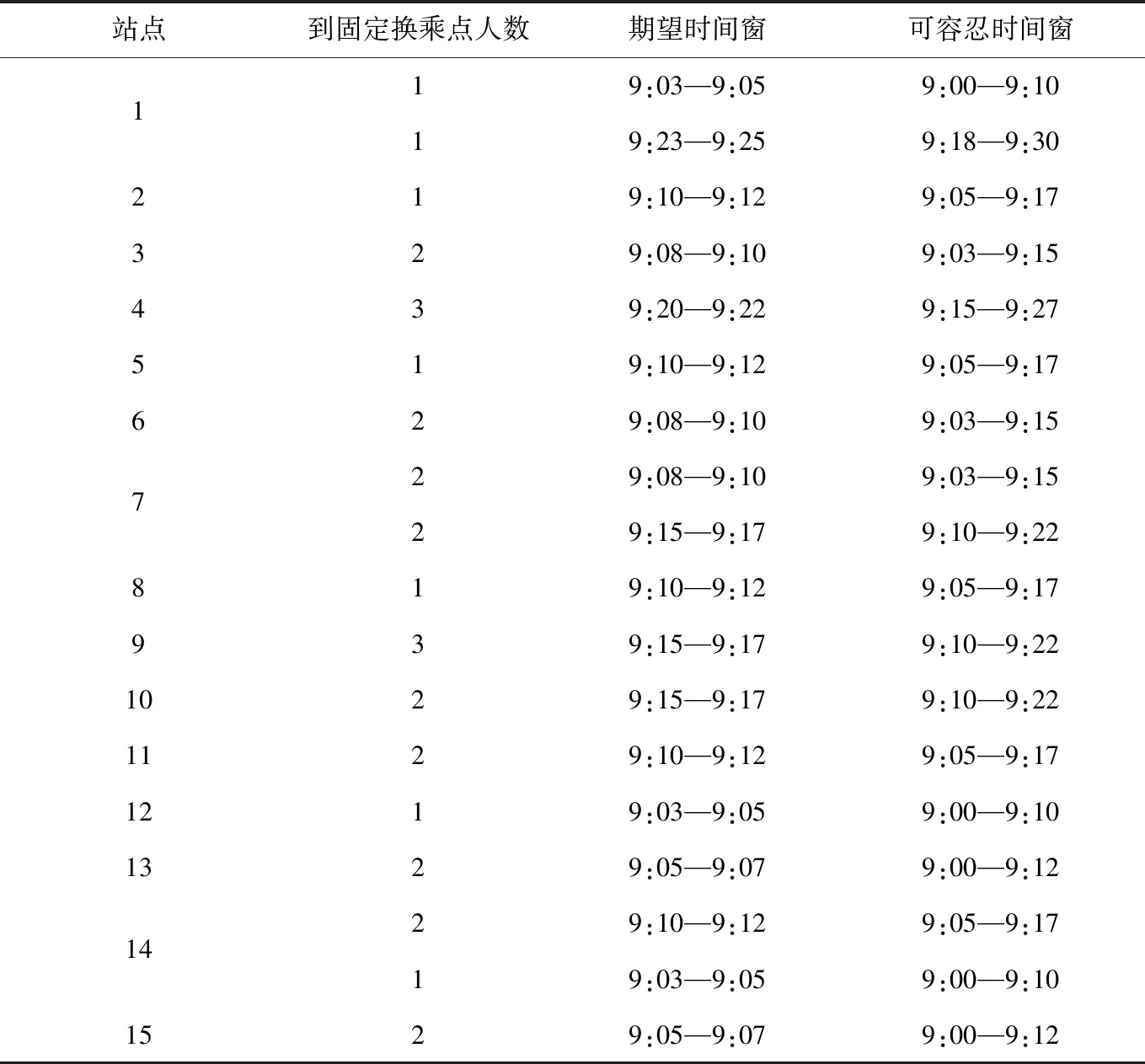
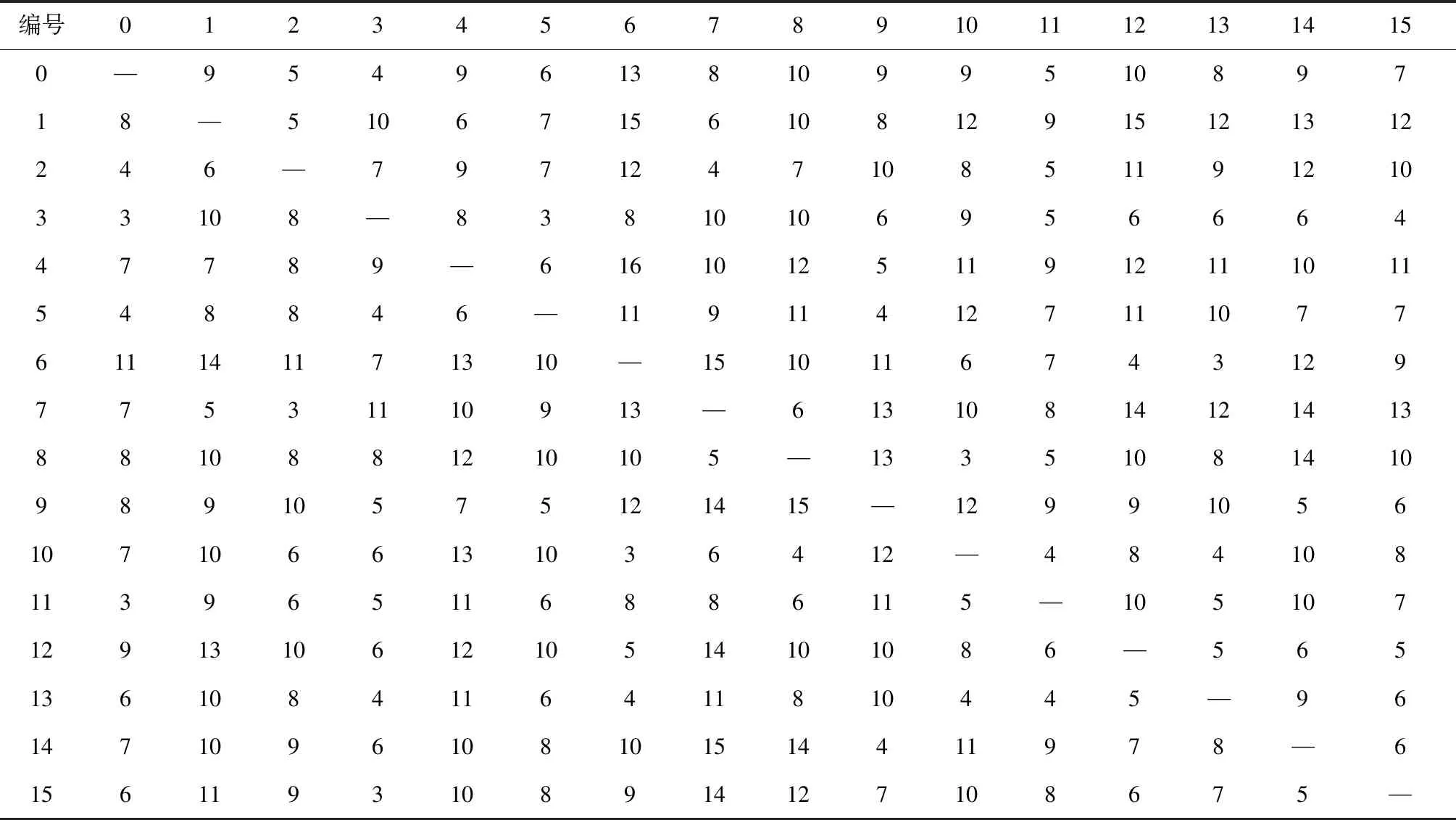
基因选择采用轮盘赌的方法，将各染色体适应度与所有染色体适应度和的比值作为该染色体的被选概率进行选择。假设各染色体的被选概率为Pi，Si为染色体i随机产生一个数，取值在0～1内。若Si

交叉操作采用多点交叉的方式，先随机确定多个交叉位置，然后交换相应的子串，从而产生新的个体。

变异操作采用单点变异法，即遍历种群中每个个体的编码位置，每次产生一个随机数τ。若τ小于变异概率，则对该位置进行变异操作；反之，则重新选择变异位置。

4 案例分析

为验证上述模型的有效性和可行性，构造一个小型网络进行案例分析，该模型所需的已知条件如表2～4所示。表2中给出了一些常变量的输入参数，车辆到达换乘站的时间窗约束范围为主线公交出发前2 min。表3 列出了服务区域内各需求站点的乘客预约信息。以需求点1的乘客预约信息为例进行解释，在需求点1共有2名乘客提出预约申请，他们的期望服务时间窗分别为9:03—9:05和9:23—9:25，可容忍服务时间窗分别为9:00—9:10和9:18—9:30。表4列出了服务区域内换乘站与需求点以及各需求点之间的出行时间矩阵，其中编号1～15为需求点，编号0为换乘站，各站点间的平均出行时间为在实际路网中的最短距离与车辆平均行驶速度的比值。

表2 案例中的常变量

表3 各需求点的预约信息统计表

表4 案例网络的旅行时间矩阵

运用建立的路径优化模型和设计的遗传算法，通过PYTHON软件编程对该案例进行求解，同时对比单纯使用8座车型和15座车型的输出结果进行分析，如表5所示。

表5 接驳公交行驶路线表

表5的结果表明，算例1使用了4辆车，包括3辆8座车和1辆15座车，算例2使用了5辆8座车，算例3使用了4辆15座车，其中算例1的最优适应度值最高为1.086 7。通过对比可发现，综合考虑企业运营成本最低和平均乘客满意度最高，同样的出行需求下，混合车型的路径规划结果更优，其供需匹配更为合理。采用混合车型路径优化方案与仅使用单一车型相比，其优势在于：在不超出车容量和线路长度的前提下，乘客出行需求少且距离换乘站远的需求点宜使用运营成本低的小型接驳车辆，乘客出行需求多且位置分布较集中的需求点宜使用可服务更多乘客的大容量接驳车辆，从而达到系统最优的效果。

4 结论

本文探讨了灵活型接驳公交的路径优化问题，重点考虑混合车型联合调度对接驳车辆路径优化的影响，以企业运营成本最小和乘客满意度最大为优化目标，兼顾路径规划和车辆协调调度，建立了基于混合车型的灵活型接驳公交路径协同优化模型，同时设计了遗传算法求解模型。算例结果表明，该模型适用于采用多车型的灵活型接驳公交系统，能在合理时间内求解出车辆调度方案和最优行驶路径，具有一定的实际运用价值。本文建立的模型适用于小规模的主线公交换乘点的接驳公交线路设计及调度方案优化，作为一类典型的NP-hard问题，当乘客需求数较大时，算法的运算效率有待提高，后续需要进一步设计算法，提高实时在线的计算速度。