四种均布荷载接触形式的路面力学响应对比分析

李 浩，许新权，刘 锋，龚侥斌

(1. 长安大学 公路学院，陕西 西安 710064； 2. 广东华路交通科技有限公司，广东 广州 510420；3. 广州大学 土木工程学院，广东 广州 510006)

0 引 言

长期以来，我国的沥青路面设计一直将汽车轮胎传给路面的荷载简化为双圆垂直均布荷载[1-2]。实际上，轮胎-路面交互作用十分复杂且与诸多因素有关，如车辆轴载、轮胎充气压力、轮胎结构及路表条件等。

大量研究已表明，简单的将轮胎接触面假设为圆形不符合实际情况，圆形接触面与路面实际受力状态有很大区别。胡小弟[3]认为轮胎作用路面接触形状更接近矩形，且随荷载的增加矩形形状越明显；孙立军[4]将不同车型、不同轴载、不同作用力分布形式简化为凸型、凹型非均布矩形块；谢水友[5]认为当垂直荷载较小时，轮胎接触形式呈椭圆形，当垂直荷载较大时近似呈矩形；彭卫兵[6]认为车辆轮胎与地面的实际接触形式由一个矩形和两个半圆形组成；姚占勇[7]运用三维有限元方法分析了轮压在圆形均匀分布、矩形均匀分布和矩形非均匀分布3种轮载作用形式下，半刚性路面结构的力学响应。

综上所述，现有研究均表明轮胎接触面形状随荷载等因素的变化而呈现不同的接触形式，并分别提出了更加符合实际受力特点的接触形式，却没有进行沥青路面不同接触形式下的力学响应对比分析。

因此，笔者以云罗高速试验路结构形式为基础，利用ANSYS建立三维有限元模型，对比分析静态均布荷载作用下矩形、正方形、圆形、椭圆形四种不同接触形式对沥青路面力学响应的影响，为轮胎荷载接地形式的简化、选取提供参考和依据。

1 均布荷载接触形式简化

按文献[8]中的荷载作用面积等效原则进行接触面简化。以双圆均布荷载为基础，将加载面进行了正方形、矩形、准椭圆形三种形式的简化，根据加载面简化原理得到简化后四种荷载接触面的尺寸，如表1和图1。表1最后一行为相对于双圆均布荷载的面积偏差，可见三种荷载简化形式的相对偏差都很小，满足精度要求。

图1 简化后的均布荷载接触面尺寸(单位：mm)Fig. 1 Size of contact surface of uniformly-distributed load after simplification

2 有限元模型

2.1 计算模型

2.1.1 模型尺寸

利用ANSYS建立三维有限元模型，约定X、Y、Z分别为行车方向、深度方向、横断面方向。模型尺寸为X×Y×Z=(16×7.5×16)m，路面结构尺寸X×Z=(10×12)m，Y方向尺寸依据路面各层实际厚度而定。计算采用SOLID45等参8节点单元。

2.1.2 边界条件

路面结构X和Z方向边界无约束，本节对路面结构三维有限元模型X和Z方向施加法向位移约束，即X方向施加X方向位移约束，Z方向施加Z方向位移约束。

2.1.3 网格尺寸

分别对四种荷载接地形式划分网格，各接地荷载图形如图2。

图2 各接地荷载网格图形Fig. 2 Graphics of each grounding load grid

2.2 结构及材料参数

采用文献[9]给定的云罗高速试验路结构型式，计算的路面结构及材料参数如表2。

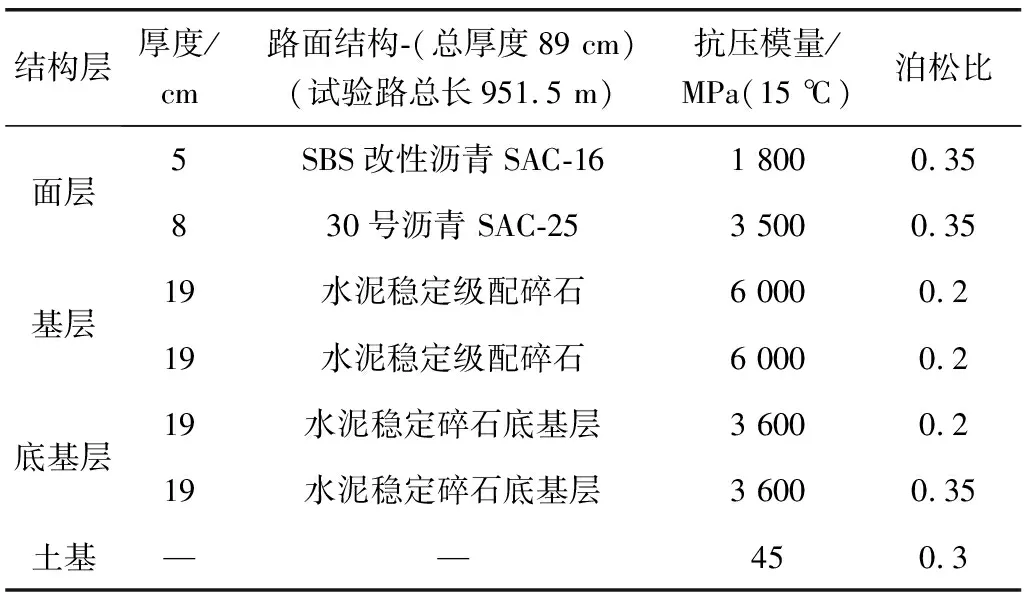
表2 路面结构型式及材料参数Table 2 Pavement structure types and material parameters

3 接触形式对路面力学指标影响

对采用ANSYS有限元对矩形、正方形、圆形、椭圆形四种均布荷载接触形式的沥青路面，进行力学响应对比计算和分析。定义相对偏差ω为：

(1)

表3～表8的相对偏差均按上式计算。

3.1 路表竖向位移对比

由ANSYS计算得到不同接触面形式在标准轴载作用下轮隙中心、单轮中心位移值，结果见表3。图3为不同荷载接触形式沿路面横向分布的路表竖向位移，横坐标0代表轮隙中心。

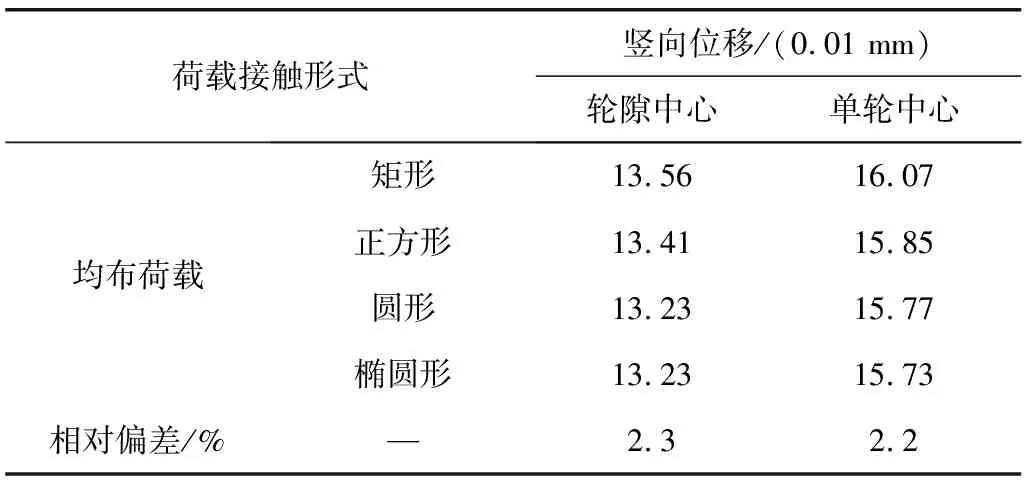
表3 不同荷载接触形式的竖向位移Table 3 Vertical displacement with different load contact types

由表3可见，轮隙中心位移：矩形>方形>圆形=椭圆；单轮中心位移：矩形>方形>圆形>椭圆。轮隙中心位移和单轮中心位移的相对偏差分别为2.3%、2.2%。

可见，在相同的接地压力作用下，矩形接触形式的轮隙中心位移、单轮中心位移均最大，方形次之，椭圆形均最小。

由图3可得，在与接触面邻近的路表两侧区域，矩形接触面竖向位移最大，正方形、椭圆形及圆形接触面较为接近。

图3 不同荷载接触形式沿路面横向分布的路表竖向位移Fig. 3 Vertical displacement of the pavement surface with differentload contact types along the transverse distribution of pavement

表4为不同荷载接触形式下，单圆荷载中心正下方随深度方向的竖向位移值。图4为竖向位移值随深度的分布。

表4 荷载中心正下方不同深度的竖向位移Table 4 Vertical displacement of different depths under load center

由表4和图4可得，单圆荷载中心正下方(面层和基层内部)不同深度的竖向位移：矩形>方形>圆形≈椭圆，竖向位移随深度增加而逐渐减小，变化规律大体一致；根据相对偏差ω计算公式，计算不同深度处竖向位移相对偏差均在3%以内，见表4。

图4 荷载中心正下方不同深度的竖向位移分布Fig. 4 Vertical displacement distribution of different depths under loadcenter

综上所述，在标准轴载作用下，相同深度和点位处的竖向位移：矩形>方形>圆形>椭圆。

3.2 面层剪应力响应对比

ANSYS计算得到的沥青层最大剪应力，结果见表5。不同接触形式的下面层剪应力均大于上面层,两者的比值在1.08～1.13之间。上、下面层最大剪应力均为：矩形>方形>圆形>椭圆，上、下面层最大剪应力的相对偏差分别为19%、14%。

表5 沥青层最大剪应力Table 5 Maximum shear stress of asphalt layer

3.3 路面各结构层层底拉应力响应对比

ANSYS计算得到的各结构层层底水平拉应力的最大值，结果见表6。

沥青层底均为压应力，最大压应力大小为：圆形>方形>矩形>椭圆形；基层底均为拉应力，基层底拉应力大小为：圆形>方形>椭圆>矩形；底基层底均为拉应力，底基层底拉应力大小为：矩形>方形>圆形>椭圆。

由各层层底横向、纵向应力的相对偏差可知，在不同接触面形式作用下，不同层位的应力响应表现不同，面层底、基层底、底基层底应力的相对偏差分别为7.9%、1.6%、15.2%。

表6 路面各结构层层底最大拉应力Table 6 The maximum tensile stress of each layer of pavement structure

3.4 路面各结构层层底拉应变响应对比

ANSYS计算得到的各结构层层底水平拉应变的最大值，结果见表7。

下面层底最大拉应变：椭圆>方形>圆形>矩形；基层底最大拉应变：矩形>方形>圆形>椭圆；底基层底最大拉应变：方形=圆形>椭圆>矩形。

由各层层底横向、纵向应变的相对偏差可知，在不同接触面形式作用下，不同层位的应变响应表现不同，面层底、基层底、底基层底应力的相对偏差分别为109%、5%、7%。

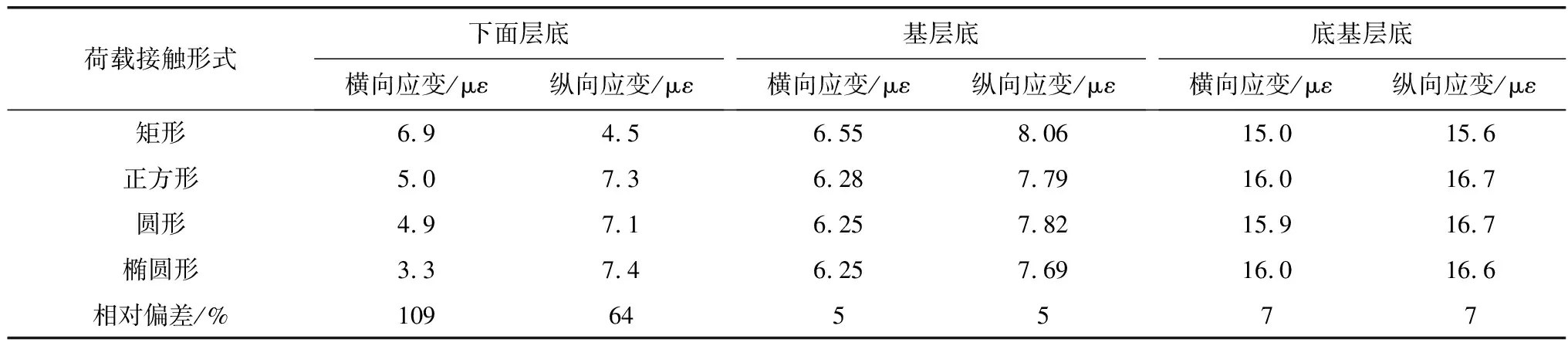
表7 路面各结构层层底最大拉应变Table 7 The maximum tensile strain of each layer of pavement structure

3.5 土基顶面压应变响应对比

ANSYS计算得到的土基顶面压应变，结果见表8。

由表8可知，土基顶面压应变大小顺序为：矩形>方形>圆形>椭圆，其相对偏差为13.4%。

表8 不同荷载接触形式的土基顶面压应变Table 8 Compressive strain on top surface of soil base with differentload contact types

4 荷载形式对路面结构设计的影响

第3节分析表明，在相同标准荷载作用下，相同层位、相同点位，力学指标的计算结果存在一定的差异。在进行沥青路面设计时，如采用不同的荷载接触形式，对于相同的路面材料，得到的疲劳寿命也会有差异。

因此，参照JTG D50—2017《公路沥青路面设计规范》[10]，对比云罗试验路在四种不同荷载接触形式下疲劳寿命差异。

2017版设计规范取消了路表弯沉这一设计指标，因此，通过路表弯沉计算得到的疲劳寿命仍然参照2006版设计规范中的计算公式，根据沥青层底拉应变、基层底拉应力、土基顶面压应变计算得到的疲劳寿命则参照2017版规范计算。此外，沥青层底应力均为压应力，不受拉应力，表明沥青层底不会产生疲劳开裂，因此，该指标不参与计算。

本次研究重点在于对比不同荷载接触形式之间疲劳寿命的相对差异，故而对疲劳寿命的具体数值不展开计算。仅以2017版设计规范中的双圆均布荷载下各指标计算的疲劳寿命为标准值，计算其他三种荷载接触形式相对于圆形荷载的比值。计算采用式(2)：

(2)

式(2)中，La为根据其它荷载接触形式的力学指标计算得到的疲劳寿命，Lb为相同力学指标下、采用双圆均布荷载计算得到的疲劳寿命；Si为相对比值，i分为矩形荷载、方形荷载和椭圆形荷载。

计算得到的S矩形、S正方形、S椭圆形如表9。

表9 Si计算结果Table 9 Si calculation results %

表9中计算结果有正有负，负数表示对应荷载形式力学指标的疲劳寿命计算值，小于双圆均布荷载计算值，反之亦然。

可见，① 除了沥青层底拉应变计算的疲劳寿命大于圆形荷载外，矩形荷载其它三个指标计算的疲劳寿命均小于圆形荷载，且相差较大，可见矩形荷载作用的影响深度贯穿整个结构层；② 方形荷载的四个指标计算得到的疲劳寿命均小于圆形荷载，但相差不大，表明按照方形荷载设计沥青路面较规范更安全，影响深度较小；③ 椭圆形荷载的四个指标计算得到的疲劳寿命均大于圆形荷载，但相差不大，表明按照椭圆形荷载设计沥青路面不如规范安全性高，影响深度也不大。

5 结 论

1)矩形荷载作用下的竖向位移、剪应力、底基层底拉应力最大，沥青层底拉应变最小，且与圆形荷载各指标计算的疲劳寿命相差较大，影响深度贯穿整个结构层。在进行沥青路面结构设计时，不建议采用矩形荷载简化形式。

2)方形、椭圆形荷载作用下，各指标的响应同圆形荷载相差不大，影响深度均不大，但采用方形荷载设计沥青路面较规范更安全，采用椭圆形荷载设计沥青路面不如规范安全性高。考虑到有限元计算中划分网格的方便，可采用方形荷载简化形式。

3)各种简化形式与圆形荷载计算结果的相对偏差有大有小，选用过程中，应根据需要和实际情况灵活选择。