均匀混响背景下抗多目标干扰恒虚警检测器设计
殷超然, 闫林杰, 郝程鹏, 孙梦茹
均匀混响背景下抗多目标干扰恒虚警检测器设计
殷超然1,2, 闫林杰1,2, 郝程鹏1, 孙梦茹1,2
(1. 中国科学院声学研究所, 北京, 100190; 2. 中国科学院大学 电子电气与通信工程学院, 北京, 100049)
为提高恒虚警(CFAR)方法的抗多目标干扰能力, 文中提出一种能够对抗多目标干扰的新型UMCASO-CFAR检测器。该检测器的特点是分别对前后沿滑窗数据使用无偏最小方差估计(UMVE)方法和单元平均(CA)方法得到2个局部估计, 然后采用最小选择(SO)处理取二者中较小的一个作为均匀混响背景功率水平估计。在Swerling II型目标假设下, 推导出均匀混响背景下UMCASO-CFAR检测器虚警概率和检测概率的解析表达式, 证明其具有CFAR性能。进一步通过解析方法、蒙特卡洛仿真和实测数据处理三方面研究了该方法在均匀混响背景和多目标环境下的性能, 结果表明相较于现有方法, UMCASO-CFAR具有更好的抗多目标干扰的性能, 而且在均匀混响背景下具有非常小的CFAR检测损失。
恒虚警; 检测器; 无偏最小方差估计; 单元平均; 最小选择; 多目标; 抗干扰; 均匀混响
0 引言
海洋环境是主动声呐的主要工作环境, 其空间较狭窄, 且海水具有很强的不均匀性, 声呐发出的声波经过水声信道会发生散射, 而所有的散射声波相互叠加会形成极强的混响。混响的非平稳性给主动声呐的自动检测带来很大困难。早期声呐检测方法采用固定检测门限, 当背景混响功率水平发生微小上升时, 虚警概率就会产生极大的波动, 有时会上升3个数量级之多[1]。因此, 急需一种能够摆脱混响功率水平波动影响、使虚警概率保持恒定的方法。恒虚警(constant false alarm rate, CFAR)检测技术就是解决上述问题的有效手段, 其基本思想是根据检测单元附近的参考单元估计背景混响的平均功率, 从而得到自适应检测阈值, 达到使虚警概率保持恒定的目的。
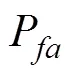
1995年, Nagle等[12]提出了无偏最小方差估计(unbiased minimum-variance estimation, UMVE)方法, 这种方法在删除掉干扰目标后, 对剩余的样本采用加权平均来得到背景功率水平估计, 有效减少了CFAR损失。文献[13]和[14]即是基于UMVE方法的2种CFAR检测器。为进一步减小计算量, 曲超等[15]提出一种改进的UMVE方法, 称为MUMCA-CFAR检测器, 其前后沿滑窗分别利用UMVE和CA方法形成2个局部估计, 然后取2个局部估计的均值作为背景功率水平估计。研究结果表明, 该方法在干扰数目较多或前后沿滑窗中均存在干扰情况下的抗干扰能力会急剧下降。
为解决MUMCA-CFAR检测器存在的不足, 文中提出一种新的CFAR检测器, 仍采用UMVE和CA方法得到2个局部估计, 与MUMCA-CFAR不同的是, 采用选小处理来得到混响的功率水平估计, 简称为UMCASO-CFAR检测器。选小处理的引入将使UMCASO-CFAR检测器具有优异的对抗多目标抗干扰的能力。
1 UMCASO-CFAR数学模型
文中研究对象是主动声呐的CFAR检测问题, 考虑一个以混响为主的背景环境, 且假设接收的混响服从白色高斯分布, 经过平方律检波器后, 其输出服从负指数分布; 各参考单元统计独立同分布, 目标类型是Swerling II型[16]。根据以上假设, 有目标时检测单元的概率密度函数(probability density function, PDF)为
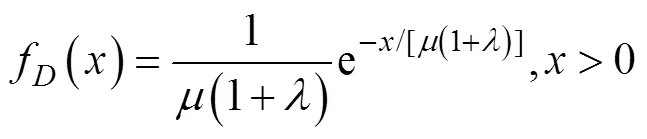
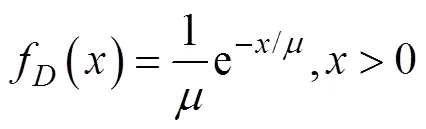
其累积分布函数(cumulative distribution function, CDF)为
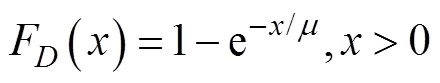
下面先介绍UMVE算法, 进一步给出UMCASO-CFAR检测器的数学模型。
1.1 UMVE方法
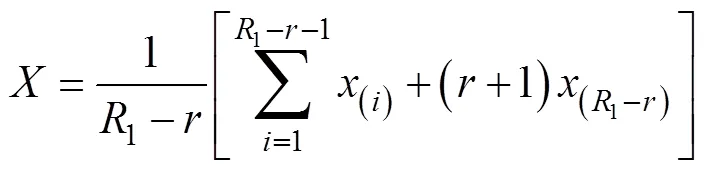

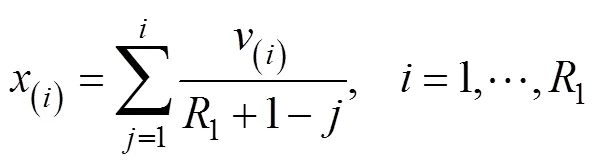
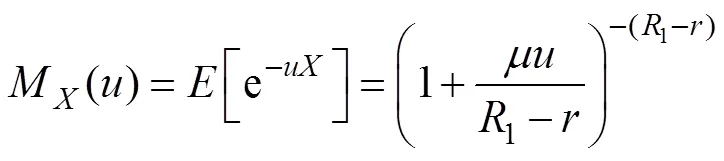

相应的CDF为

1.2 UMCASO-CFAR检测器模型


图1 UMCASO-CFAR检测器模型框图
UMCASO-CFAR检测器具体工作流程如下:
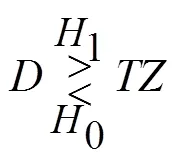
2 均匀混响背景下虚警概率和检测概率
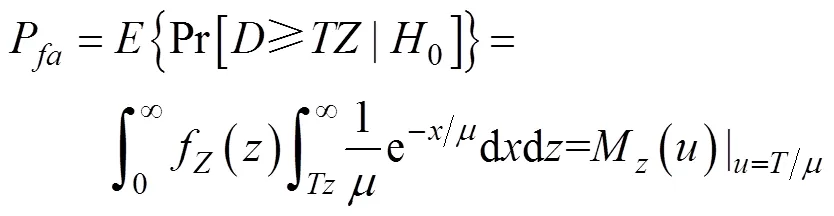

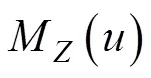

其PDF和CDF分别为
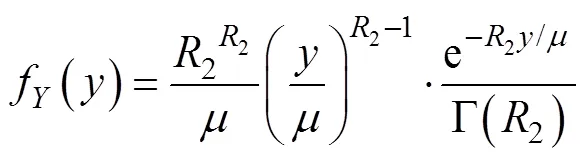
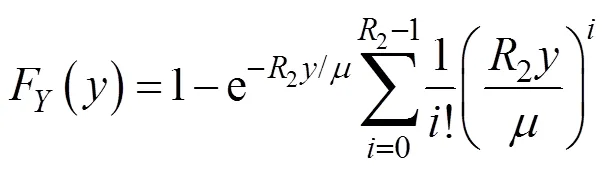
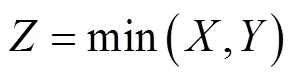
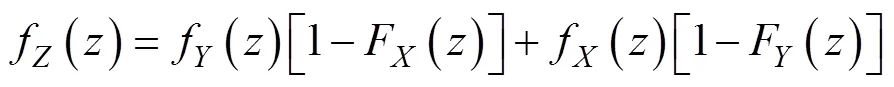
其矩母函数为

经过推导可得
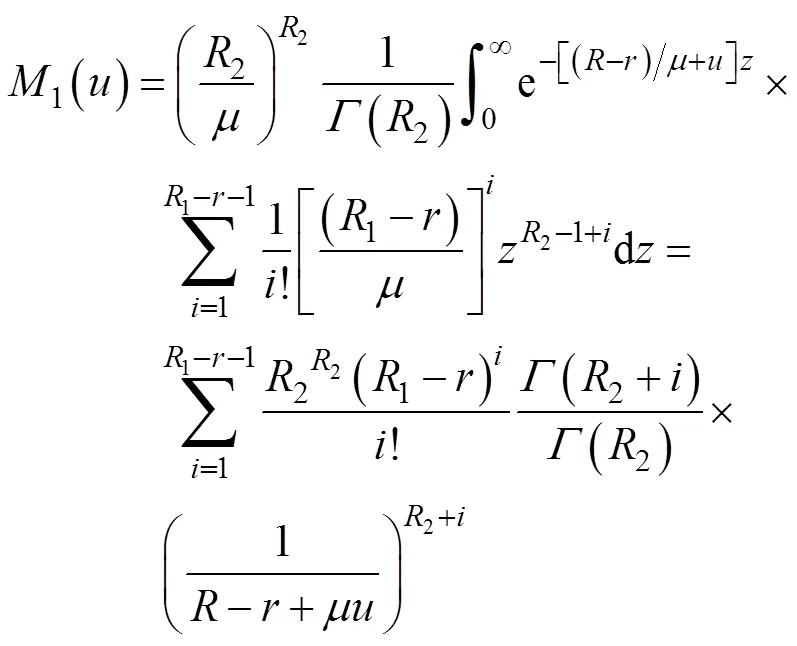
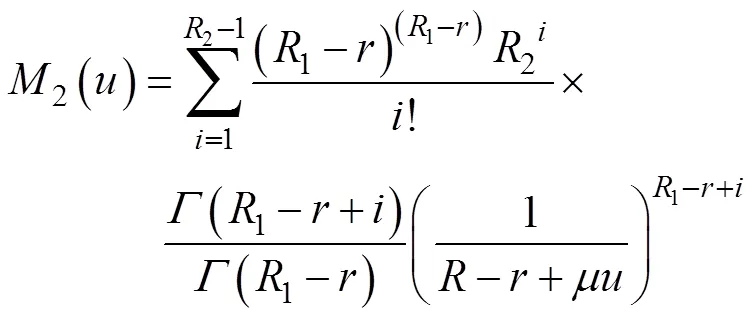
将式(18)~(20)带入式(11)可得UMCASO- CFAR的虚警概率为


根据式(12), 均匀混响背景下UMCASO- CFAR的检测概率为
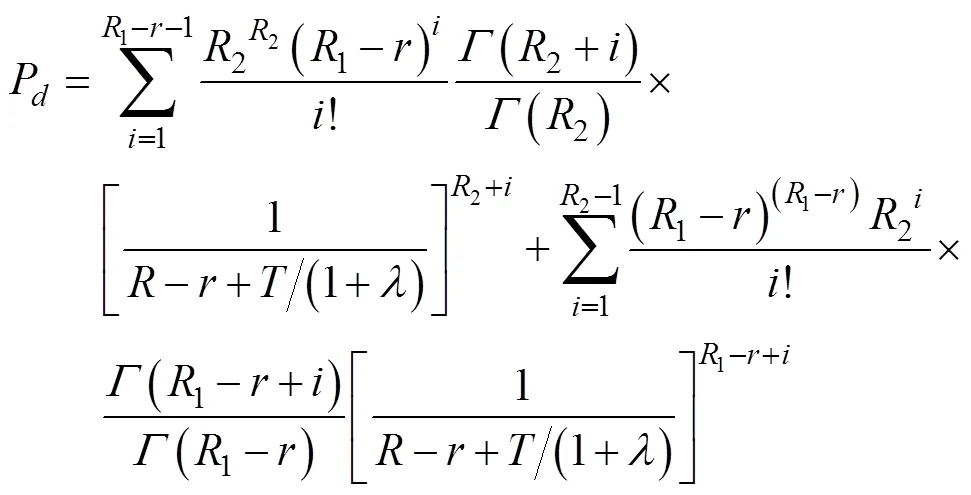
3 UMCASO-CFAR检测性能
分别采用解析方法、蒙特卡洛仿真方法和实测数据对UMCASO-CFAR的检测性能进行分析。均匀混响背景下的检测性能是通过式(22)计算得到, 而对于多目标环境, 由于无法得到检测概率的闭式解, 可通过蒙特卡洛仿真得到, 最后采用实测数据做进一步验证。
为体现UMCASO-CFAR的优越性, 分析中还增加了与MOSCA-CFAR和MUMCA-CFAR 2种现有检测器的对比。其中MOSCA-CFAR由文献[9]提出, 它是对前后沿参考滑窗分别使用OS和CA方法得到2个局部估计, 然后取二者的均值(mean)作为背景功率水平估计。
3.1 均匀混响背景

图2给出的是3种检测器在均匀混响背景下检测性能的仿真结果。从图中可以看出, 3种检测器在均匀背景中的检测性能非常相近, 其中MUMCA-CFAR和MOSCA-CFAR之间差距极小, 很难分辨, UMCASO-CFAR与二者相比附加检测损失小于0.1 dB。

图2 均匀混响背景下3种检测器检测性能
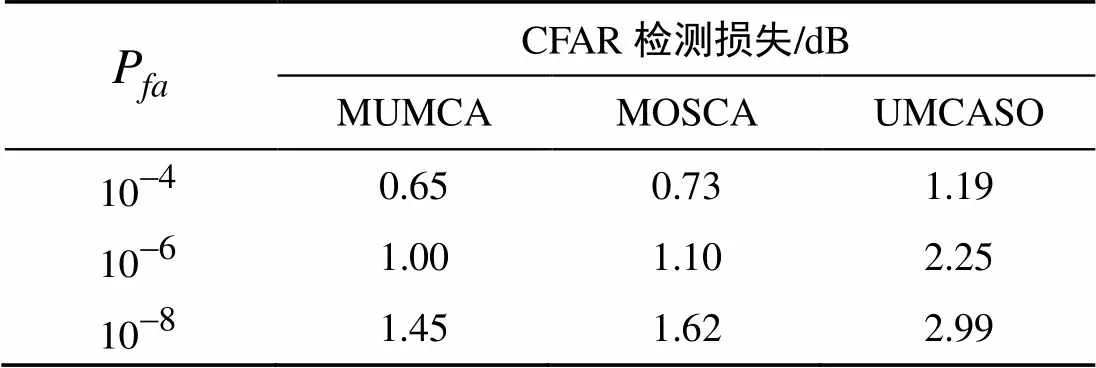
表1 均匀混响背景下3种检测器CFAR检测损失
3.2 多目标环境
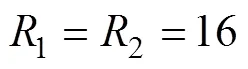
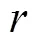
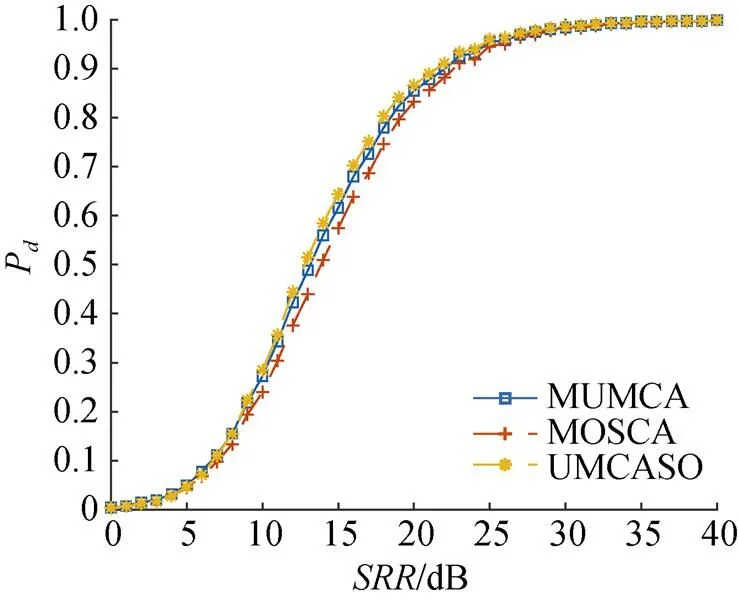
图3 IL=4, IR=0时3种检测器检测性能
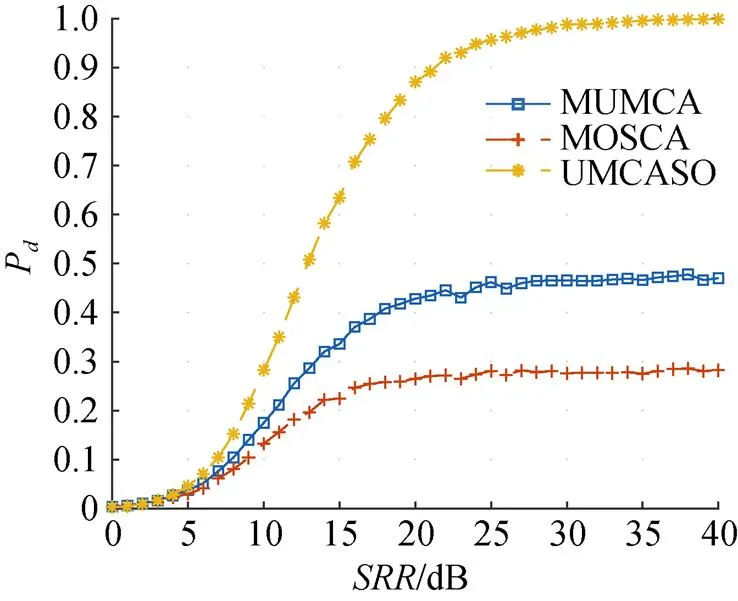
图4 IL=6, IR=0时3种检测器检测性能
另一方面, 虽然MUMCA-CFAR检测器加入了停止移位寄存器, 使进入后沿滑窗的干扰目标数大大下降, 但是干扰目标仍存在一定的概率进入后沿滑窗。图5就是考虑后沿滑窗也存在干扰目标(=4,=4)时UMCASO-CFAR、 MUMCA- CFAR和MOSCA-CFAR的检测性能。由图5可以看出, 由于后沿滑窗使用CA方法, MUMCA- CFAR没有抗干扰的能力, 故当干扰目标进入后沿滑窗后其检测性能大幅下降, 但是加入了取小逻辑的UMCASO-CFAR在此时的检测性能依然稳健。值得注意的是,=40 dB时, MUMCA- CFAR和MOSCA-CFAR能达到的检测概率仍不足0.3。

图5 IL=4, IR=4时3种检测器检测性能

表2 多目标环境下3种检测器CFAR检测损失
3.3 实测数据
利用实测数据对UMCASO-CFAR的检测性能进行验证。该数据是某均匀线列阵声呐所采集的混响数据, 阵元个数为7个, 探测海域平均深度80 m, 探测深度35 m, 声呐平台运动速度10 m/s。每个通道采样数据长度为25001。
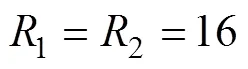
实测数据处理结果见图6~图7。其中图6给出了均匀混响背景下的性能曲线, 可以看出此时UMCASO-CFAR检测器相较于另外2种检测器性能十分接近, 仅有一个很小的附加损失。
图7(a)是前沿滑窗添加4个干扰的情况, 图7(b)是前沿滑窗添加6个干扰的情况。可以看出, 图7(a)中UMCASO-CFAR与MUMCA-CFAR几乎相同, 均优于MOSCA-CFAR, 图7(b)中UMCASO-CFAR明显最优, 在高SRR下, MUMCA和MOSCA已不能正常工作。图7(c)是在前后沿滑窗中均添加4个干扰时实测数据得到的结果, 同样令=。可以看出, 当前后沿滑窗均添加干扰时, 高信混比下MUMCA和MOSCA已无法正常工作, 而UMCASO-CFAR检测器性能可以保持正常。
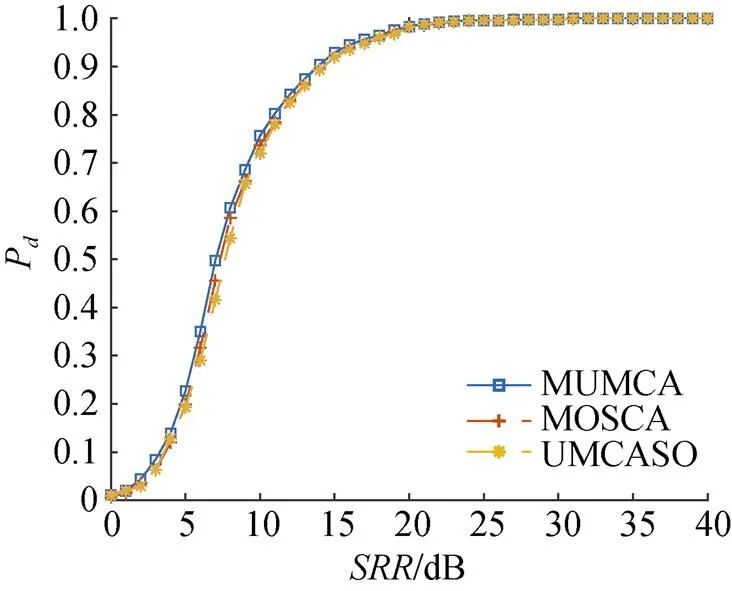
图6 均匀混响背景下3种检测器实测数据结果

图7 3种检测器实测数据结果
图6~图7的结果均与3.1节和3.2节中的仿真结果一致。进一步证明了仿真结果的有效性, 尤其是UMCASO-CFAR检测器具有很强的抗干扰能力。
4 结束语

[1] 何友, 关键, 孟祥伟, 等. 雷达目标检测与恒虚警处理[M]. 第2版. 北京: 清华大学出版社, 2011.
[2] Finn H M, Johnson R S. Adaptive Detection Mode with Threshold Control as a Function Spatially Sampled Clutter-Level Estimates[J]. RCA Review, 1968, 29: 414-464.
[3] Trunk G V. Range Resolution of Targets Using Automatic Detectors[J]. IEEE Trans. on AES, 1978, 14(5): 750-755.
[4] Hansen V G. Constant False Alarm Rate Processing in Search Radars[C]//IEEE International Radar Conference. London: IEEE, 1973: 325-332.
[5] 郝程鹏, 司昌龙, 原建平, 等. 一种新的基于CM和CA的恒虚警检测器[J]. 弹箭与制导学报, 2007, 27(2): 309-312.Hao Cheng-peng, Si Chang-long, Yuan Jian-ping, et al. A Novel CFAR Detector Based on Censored Mean and Cell Averaging[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(2): 309-312.
[6] 吉书龙, 皇甫堪, 周良桂, 等. 一种新的雷达恒虚警(CFAR)处理器[J]. 国防科技大学学报, 1990, 12(4): 116- 121.Ji Shu-long, Huang-fu Kan, Zhou Liang-gui, et al. A New Radar Constant-False-Alarm-Rate(CFAR) Processor[J]. Journal of National University of Defense Technology, 1990, 12(4): 116-121.
[7] Rohling H. Radar CFAR Thresholding in Clutter and Multiple Target Situations[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, 19(4): 608-621.
[8] Rohling H. Ordered Statistic CFAR Technique—an Overview[J]. 雷达科学与技术, 2012, 10(2): 117-123.
[9] 何友, Rohling H. 两种具有自动筛选技术的广义有序统计恒虚警检测器及其在多目标环境下的性能[J]. 电子科学学刊, 1994, 16(6): 582-590.He You, Rohling H. Performance of Two Generalized Order Statistics CFAR Detectors with Automatic Censoring Technique in Multiple Target Situations[J]. Journal of Electronics, 1994, 16(6): 582-590.
[10] He Y. Performance of Some Generalized Modified Order Statistics CFAR Detector with Automatic Censoring in Multiple Target Situations[J]. IEE Proceedings-Radar, Sonar and Navigation, 1994, 141(4): 205-212.
[11] 何友, 关键, Rohling H. 一种基于排序和平均的新恒虚警检测器[J]. 现代雷达, 1995, 17(4): 33-36.He You, Guan Jian, Rohling H. A New CFAR Detector Based on Ordered Statistics and Averaging[J]. Modern Radar, 1995, 17(4): 33-36.
[12] Nagle D T, Saniie J. Performance Analysis of Linearly Combined Order Statistic CFAR Detectors[J]. IEEE Trans. on AES, 1995, 32(2): 522-533.
[13] 郝程鹏, 侯朝焕. 基于UMVE算法的恒虚警检测器[J].现代雷达, 2007, 29(7): 38-40. Hao Cheng-peng, Hou Chao-huan. CFAR Detector Based on Unbiased Minimum-variance Estimation Algorithm[J]. Modern Radar, 2007, 29(7): 38-40.
[14] 郝程鹏, 侯朝焕. 一种新的基于UMVE和OS的恒虚警检测算法[J]. 电子与信息学报, 2007, 29(6): 1380-1383.Hao Cheng-peng, Hou Chao-huan. A Noval CFAR Algorithm Based on Unbiased Minimum-Variance Estimation and Ordered Statistics Estimation[J]. Journal of Ele- ctronics & Information Technology, 2007, 29(6): 1380- 1383.
[15] 曲超, 郝程鹏, 杨树元. 一种新的基于UMVE和CA的恒虚警检测器[J]. 计算机仿真, 2008, 25(9): 321-323.Qu Chao, Hao Cheng-peng, Yang Shu-yuan. A Novel CFAR Detector Based on Unbiased Minimum-Variance Estimation and Cell Averaging[J]. Computer Simulation, 2008, 25(9): 321-323.
[16] Swerling P. Probability of Detection for Fluctuating Targets [J]. IRE Trans. on IT, 1960, 6(2): 269-308.
Design of a Multi-Target Interference Resistant Constant False Alarm Rate Detector for Homogeneous Reverberation Background
YIN Chao-ran1,2, YAN Lin-jie1,2, HAO Cheng-peng1, SUN Meng-ru1,2
(1. Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China; 2. School of Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China)
To improve the ability of constant false alarm rate(CFAR) method against interference of multiple targets, a new CFAR detector is designed. The unbiased minimum-variance estimation(UMVE) method and the cell average(CA) method are applied to the data of left and right reference windows to obtain two local estimates, and then the smaller of(SO) two is taken as the power level estimate of homogeneous reverberation background. Under the assumption of Swerling II target, the closed-form formulas of the UMCASO-CFAR detector’s false alarm probability and detection probability in homogeneous reverberation background are derived,CFAR property of the detector is proved. Further, the performances of the detector in both homogeneous background and multi-target environment are discussed by means of analytical method, Monte Carlo simulation and measured data processing. The results show that compared with the existing methods, the UMCASO-CFAR detector has higher capability to resist multi-target interference, and ensures a very small CFAR detection loss in homogeneous reverberation background.
constant false alarm rate(CFAR); detector; unbiased minimum-variance estimation(UMVE); cell-ave- rage(CA); small of(SO); multi-target; interference resistant; homogeneous reverberation
TJ630.34; TN911.7
A
2096-3920(2019)04-0434-08
10.11993/j.issn.2096-3920.2019.04.011
殷超然, 闫林杰, 郝程鹏, 等. 均匀混响背景下抗多目标干扰恒虚警检测器设计[J]. 水下无人系统学报, 2019, 27 (4): 434-441.
2018-11-19;
2019-05-18.
国家自然科学基金项目资助(61571434).
殷超然(1996-), 男, 在读博士, 主要研究方向为信号与信息处理.
(责任编辑: 陈 曦)

