w－算子的盖包

张晓磊

(成都航空职业技术学院基础教学部，四川成都610100)

1 预备知识

本文中，R是交换结合环，M+表示M的特征模HomZ(M，Q/Z)．一个模类F称为预盖类，如果对任意R－模M，存在一个同态f:F(M)→M，其中F(M)∈F，使得对任意F∈F，g:F→M都有如下交换图．此外，如果使分解f=fοh成立的h只有同构，则称F为盖类．对偶的，可以定义预包类和包类．自从结合环上的任意模都有内射包被证明后，模类的盖包问题在代数研究中受到广泛关注．在试图解决内射包的对偶问题中，Bass［1］证明了每个模有投射盖当且仅当基环是完全环．

1979 年，Salce［2］发现盖包问题可以用余挠对来解决．一对模类(F，C)称为余挠对，如果 F┴=C并且，其中

余挠对(F，C)称为完全的，如果F是盖类并且C是包类;称为遗传的，如果F关于满态射的核封闭．Eklof等［3］证明了任意由集合余生成的余挠对都是完备的．用这种方法，Bican等［4］证明了平坦余挠对是完全的，从而完全解决了著名的平坦盖猜想:任意结合环上，每个模都有平坦盖．

纯正合列与余挠对密切相关，一个R－模正合列0→N→M→L→0称为纯正合列，如果对任意R－模 A，0→AN→AM→AL→0是正合的．此定义当且仅当对任意有限表现R－模B，0→HomR(B，N)→HomR(B，M)→HomR(B，L)→0 正合;当且仅当正合列0→L+→M+→N+→0可列．此时，称N是M的纯子模，L是M的纯商模．

Holm等［5］的定理3．4总结了纯性与完全余挠对的关系得到了如下结果．

定理1．1 设F是R－模类，F包含基环R，关于扩张、直和、纯子模和纯商模封闭，则(F，F┴)是完全的余挠对，因此F是盖类．

同样，Enochs 等［6］的引理 5．3．12、推论 6．2．2 和推论5．2．7给出了一种验证给定模类是预包类与包类的方法．

引理1．2 设 M和 N是 R－模，则存在只与Card(N)和Card(R)有关的基数κα，使得对任意同态f:N→M，存在一个M的纯子模S使得f(N)∈S和 Card(S)≤κα．

定理1．3 设模类F在直积下封闭，R－模M满足Card(M)=κβ，如果存在无穷基数κα使得如果F∈F和S∈F，其中，Card(S)≤κβ，则存在 F 的子模G满足G∈F且Card(G)≤κα，则M必有F－预包．

定理1．4 设模类F关于直和项和反向极限封闭，如果R－模M有F－预包，则M有F－包．

关于广义的平坦模的盖包问题研究，已经有许多人做了大量的工作，例如相对平坦模类、强平坦模类与Gorenstein平坦模类的盖包问题研究，详细内容可以参考文献［7－10］．随着星型算子的快速发展，1997年，Wang等［11］引进了整环上 w－模的概念．Wang［12］定义了整环上的 w－平坦模的概念．2011年，Yin等［13］将这些工作推广到一般交换环上．2016年，Kim等［14］定义了一般交换环上的w－平坦模．

在本文中，记由所有w－模构成的模类为W，所有w－平坦模构成的模类为Fw，并研究了w－模类和w－平坦模类的余挠与盖包问题．本文第二节解决w－模的盖包存在性问题并给出如下结果．

定理1．5 若交换环R所有的GV－理想都是有限表现的，则(W，W┴)是遗传完全余挠理论，因此W是盖类．

定理1．6 对于任意交换环R，所有w－模构成的模类W是包类．

此外，发现对于GV－无挠模，其同调意义下的w－包与经典意义下的w－包络(文献［14］的定义6．2．1)一致．本文第3节解决w－平坦模的盖包问题，得到如下定理．

定理 1．7 对任意交换环R，(Fw，Fw┴)是遗传完全余挠理论，从而Fw是盖类．

定理1．8 Fw是预包类当且仅当Fw关于直积封闭．

2 w－模的盖包性质

本节给出了w－模的概念和基本性质，并对这个模类的余挠理论与盖包理论进行研究．

定义2．1 1)交换环R的有限生成理想J称为GV－理想，若自然映射:R→J*=HomR(J，R)是同构，R的所有GV－理想构成的集合记为GV(R)．

2)设M是一个R－模，定义Torgv(M)={x∈M|Jx=0，存在 J∈GV(R)}．

3)如果Torgv(M)=M，则称M为GV－挠模;如果Torgv(M)=0，则称M为GV－无挠模．

定义2．2 1)一个GV－无挠模称为w－模，如果对任意 J∈GV(R)，Ext1(R/J，M)=0．所有的 w－模构成的模类记为W．

2)若理想I是w－模，则称I为w－理想．如果m是一个极大的w－理想，则记m∈w－Max(R)．

3)设M是一个GV－无挠模，定义Mw={x∈Ei∈IMi是w－模当且仅当对任意i，Mi是w－模;

3)由文献［15］，w－模类在直向极限与逆向极限下封闭，由此，平坦模是w－模;

4)所有的极大w－理想是素理想，M是GV－挠模当且仅当对任意m∈w－Max(R)，都有Mm=0．

根据文献［6］的引理 5．3．12、推论 6．2．2 和推论5．2．7，纯性对于模类的盖包研究有着非常重要的意义．对于w－模，首先有下面2个引理．

引理2．4 对于任意交换环，w－模的纯子模还是w－模．

证明 设0→N→M→L→0是R－模纯正合列，M是一个w－模，则N是一个GV－无挠模．考虑长正合列

0→ Hom(R/J，N) → Hom(R/J，M) →Hom(R/J，L) → Ext1(R/J，N) → Ext1(R/J，M)，由于N是M的纯子模，R/J是有限表现模，所以自然态射 Hom(R/J，M)→Hom(R/J，L)为满态射．由于M是w－模，所以 Ext1(R/J，M)=0，因此由上述正合列得Ext1(R/J，N)=0，所以N是w－模．

引理2．5 若交换环R所有的GV－理想都是有限表现的，则w－模的纯商模还是w－模．

证明 设0→N→M→L→0是R模纯正合列，即0→L+→M+→N+→0为可裂正合列，所以M+L+N+．如果 M 是 w－模，则

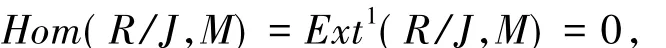
因此

如果J是有限表现理想，则

所以

从而

即L是w－模．

定理2．6 若交换环R所有的GV－理想都是(M)|Jx∈M存在J∈GV(R)}，并称之为M的w－包络．

注2．3 本文用到如下事实:

1)一个模M是w－模当且仅当对任意J∈GV(R)，HomR(R/J，M)=Ext1R(R/J，M)=0;

2)R 是 w － 模，则∏i∈IMi是w－ 模当且仅当有限表现的，则(W，W┴)是遗传完全余挠理论，因此W是盖类．

证明 对于完全余挠理论，只须验证定理1．1的条件．根据注 2．3，R 是 w－模，w－模关于直和和扩张封闭．由引理 2．4，w－模的纯子模还是 w－模，由引理2．5，由于交换环R，所有的GV－理想都是有限表现的，所以w－模的纯商模还是w－模．对于遗传余挠理论，假设0→N→M→L→0，其中M与L是w－模，则由文献［14］定理6．17得 N 是 w－模．

定理2．7 对于任意交换环R，所有w－模构成的模类W是包类．

证明 设M是R－模，基数Card(M)=κβ．对任意F∈W，S∈F，由引理1．2，存在只与 S和 R有关的基数κα和F的纯子模G满足S∈G和Card(G)≤κα．由引理 2．4，G∈W．由引理 1．3，M 有 W－预包．由定理2．3的情况3)，W在反向极限下封闭．因此，由定理1．4，模类W是包类．

设M是一个R模，则在同构意义下，存在唯一的W－包，下面给出其构造．首先考虑GV－无挠情形．

证明 设W是一个w－模，则

考虑正合列

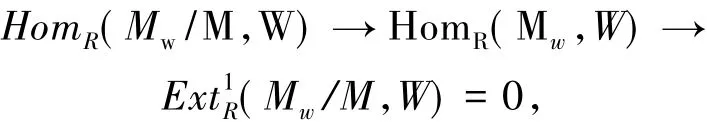
设模同态 g:Mw→Mw满足=gο．由于 Mw∈E(M)，=gο是M的本质扩张，所以g是单射．于是 Im gMw，Im g也是w－模．又因Mw是包含M的最小的w－模，所以Im g=Mw，故而g是满射．因此g为同构．

由引理2．8可得，对于GV－无挠模，其同调意义下W－包与传统意义下的w－包络(文献［14］的定义6．2．1)是一致的．下面考虑一般情形．

证明 设T=Torgv(M)考虑正合列0→T→M→M/T→0 和 0→M/T→(M/T)w→L→0．对任意 w－模W，用函子HomR(－，W)作用到上面2个正合列，得到长正合列

与

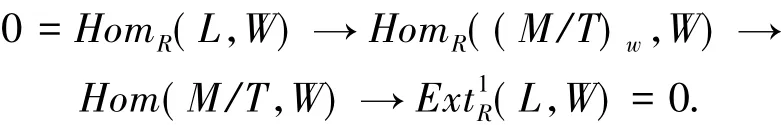
所以，HomR((M/T)w，W)→HomR(M，W)→0，即是预包．

设 g:(M/T)w→(M/T)w满足=gο，即 hοf=gοhοf．由于 f是满同态，所以 h=gοh．所以由引理 2．8得g为同构．

3 w－平坦模的盖包性质

本节给出了w－平坦模的概念和基本性质，并对这个模类的余挠理论与盖包理论进行研究．

定义 3．1 1)一个R－模同态f:A→B称为w－单射(w－满射，w－同构)，如果对任意 m∈w－Max(R)，都有fm:Am→Bm是单射(满射，同构);

2)一个模同态序列A→B→C称为w－正合列，如果对任意m∈w－Max(R)，Am→Bm→Cm是正合列;

3)R－模M称为w－平坦模，如果对任意w－单射f:A→B，1f:MA→MB还是 w－单射．记 w－平坦模类为Fw．

引理3．2 设R是交换环，则下面各条等价:1)M是w－平坦模;

3)M是w－局部平坦的，即对任意m∈w－Max(R)，Mm是平坦Rm模;4)对于任意R－模N，TorR1(M，N)是GV－挠模;5)对于任意R－模N，TorRn(M，N)是GV－挠模．证明 参见文献［14］的定理 6．7．3．

定理3．3 1)平坦模是w－平坦模，特别的R是w－平坦模;

2)w－平坦模关于扩张，满态射的核封闭;3)w－平坦模关于直和封闭．

证明 1)由w－平坦模的定义直接可得．

2)设0→N→M→L→0为R模正合列，则对任意m∈w－Max(R)，存在长正合列如果N、M是w－平坦模，则

所以M是w－平坦模．如果M、L是w－平坦模，则

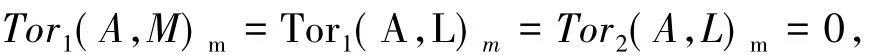
所以N是w－平坦模．

3)设 Fi是 w－平坦模，则对任意 m∈w－Max(R)和 R－模 A，

定理3．4 w－平坦模的纯子模和纯商模都是w－平坦模．

证明 设f:A→B是w－单射，则对任意极大w－理想m，可设短正合列0→Am→Bm→Cm→0也是纯正合列，故有如下行列均正合的交换图，由蛇形引理，自然同态MAm→MBm和LAm→LBm都是单射，所以M、L都是w－平坦模．

定理 3．5 对任意交换环R，(Fw，Fw┴)是遗传完全余挠理论，从而Fw是盖类．

证明 对于完全余挠理论，只须验证定理1．1的条件．根据引理3．3，R 是 w－平坦模，w－平坦模关于直和和扩张封闭．由引理3．4，w－平坦模的纯子模与纯商模是w－平坦模．对于遗传余挠理论，假设0→N→M→L→0，其中M与L是w－平坦模，则由引理3．3的情况2)得，N是w－平坦模．

定理3．6 Fw是预包类当且仅当Fw关于直积封闭．

证明 设M是一个R－模，Card(M)≤κβ，由引理1．2，存在无穷基数 κα使得若 F是 w－平坦模，S是F的子模满足Card(S)≤κβ，则存在F的纯子模G 满足 Card(G)≤κα，所以根据引理 3．4，G 是一个w－平坦模．因此，由定理 1．3，如果 Fw关于直积封闭，M有一个w－平坦预包．