钢桁架人行桥行人风环境及抗风性能研究

陈以荣， 曹 张， 刘志文， 张运权， 谢普仁

(1.上海市政工程设计研究总院(集团)有限公司，上海 200092; 2. 湖南大学 风工程与桥梁工程湖南省重点实验室，长沙 410082； 3. 长沙市芙蓉区城市建设投资有限公司，长沙 410005)

城市人行桥在满足功能的前提下对美观十分关注，其结构外形一般比较新颖美观，当跨度较大时尚需考虑风致振动与人致振动问题[1]。目前关于人行桥风致振动的研究多侧重于悬索桥、斜拉桥等桥型。许福友等[2]以主跨为105 m宿迁黄河公园景观桥为依托，对人行悬索桥涡振性能、颤振和抖振等问题进行了试验研究，对抖振分析中峰值因子的合理取值进行了探讨。白桦等[3]分别以日本九重梦人行悬索桥和国内某人行悬索桥为工程依托，对人行悬索桥抗风性能改善的气动控制措施进行了研究。Taylor等[4]对英国北部一条公路上的人行桥动力特性及气弹稳定性采用离散涡方法进行了研究，通过调整栏杆平板角度、数量等提升桥梁断面颤振稳定性，以满足桥梁颤振稳定性要求。Pirner[5]针对跨径为252 m的一座人行悬索桥进行了气弹模型试验研究，结果表明该桥在15～17.5 m/s风速范围内存在涡激共振现象，并在栏杆处设置阻尼器以控制涡振，试验未观测到颤振失稳现象。Cammelli等[6]以英国一座跨径为115 m的人行桥为对象进行了风洞试验研究，试验发现该桥存在明显的涡振—驰振耦合现象，导致该桥在设计风速范围内存在较大的风致振动响应，最后建议增加主梁刚度、质量、阻尼等以减小桥梁结构风致振动响应。

行人舒适度是城市人行桥重点关注的内容，人致振动与行人风环境都会影响人行桥的行人舒适度。以往研究主要关注桥梁结构人致振动对行人舒适性的影响，而关于风环境对行人舒适度的影响关注较少。Ingólfsson等[7]综述了易由人群荷载产生的侧向振动对行人舒适度的影响，重点对行人行为机制与原理以及行人与桥梁结构振动耦合效应进行了探讨；陈政清等[8]则从人行桥的人致振动基本理论以及动力设计方法出发，对人行桥减振设计方法及原理作出了系统总结，为解决振动带来的行人行走舒适性问题提供了支撑。在建筑领域行人风环境已被广泛采用为评估城市行人舒适度的主要指标。Stathopoulos[9]采用典型建筑群模型对行人风环境进行了风洞试验与数值模拟研究，提出了评价城市行人风环境的方法，指出城市行人风环境主要受到建筑附近风速值的影响，温度和相对湿度也是影响行人风环境的重要因素。Blocken等[10]对行人风环境研究方法进行了综述，指出尽管LDA(Laser-Doppler Anemometry)和PIV(Particle-Image Velocimetry)方法具有更高的精度，但从计算效率和成本的角度考虑建议采用边界层风洞试验与CFD(Computational Fluid Dynamics)数值模拟进行行人风环境研究。Metje等[11]认为行人舒适性具有较强主观性，采取问卷调查形式得到了英国伯明翰地区不同年龄、不同性别以及来自不同国家的行人在不同气候条件下关于舒适度的反馈。研究表明：温度和风速是影响行人舒适性的主要因素。

综上所述，人行桥结构的抗风性能与行人风环境是人行桥需要重点关注的问题。本文以一座曲线钢桁架人行桥为工程依托，采用CFD数值模拟和风洞试验相结合的方法对该桥行人风环境和结构抗风性能进行研究。

1 工程简介

在建的长沙市浏阳河人行桥是一座主跨为120 m的钢桁架曲线城市人行桥，其跨径布置为49.54 m+120 m+54.46 m=224 m，桥轴线平面曲线半径为R=200 m。该桥效果图如图1所示。该桥分两层，上层桥面布置为人行道和景观带，下层布置为非机动车道和景观文化墙，主桁断面高度为7.5 m，外侧桁高为9.2 m，桁高沿桥轴线方向渐变，主梁断面如图2所示。桥位基本风速V10=25.6 m/s，地表粗糙类别为B类，地表粗糙度系数α=0.16。对应主梁高度处的设计基准风速为Vwd=28.2 m/s，成桥状态的颤振检验风速[Vcr]=45.8 m/s。

图1 人行桥效果图Fig.1 Effect drawing of the pedestrian bridge

图2 主梁标准断面图(mm)Fig.2 Standard cross section of the main girder (mm)

考虑到该桥主跨跨径达120 m，且主梁断面内侧矮外侧高、主梁桁架外侧弦杆之间设置了文化墙，这些因素均有可能对主梁断面的气动性能产生不利影响，故在初步设计阶段采用CFD数值模拟对该桥抗风性能进行研究，以进一步认识不对称桁架主梁断面气动性能以及桥面行人风环境情况。

2 桁架断面桥面风环境与气动力数值模拟

2.1 计算域及边界条件

采用大型流体力学软件ANSYS Fluent对主梁断面流场和气动力系数进行数值模拟。根据经验桁架主梁标准断面取桁架主梁节段节间中央截面，图3所示为主梁标准断面CFD计算示意图。图4所示为主梁标准断面计算域及边界条件示意图。计算域入口边界距断面中心位置为5B(B为断面宽度)，计算域出口距断面中心位置为15B，上、下两侧边界距断面中心为5B，钢桁架计算断面的阻塞率为3.48%，满足阻塞率小于5%的要求。边界条件确定如下：计算域左侧边界为速度入口边界(Velocity-inlet)，来流风速为V∞=10 m/s，计算域右侧边界为压力出口边界(Pressure-out)，计算域上、下侧边界为对称边界(Symmetry)，主梁断面表面设置为无滑移固定壁面边界条件(Wall)。

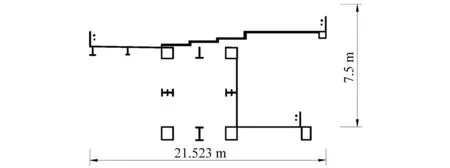
图3 主梁标准断面图Fig.3 Standard section of the main girder

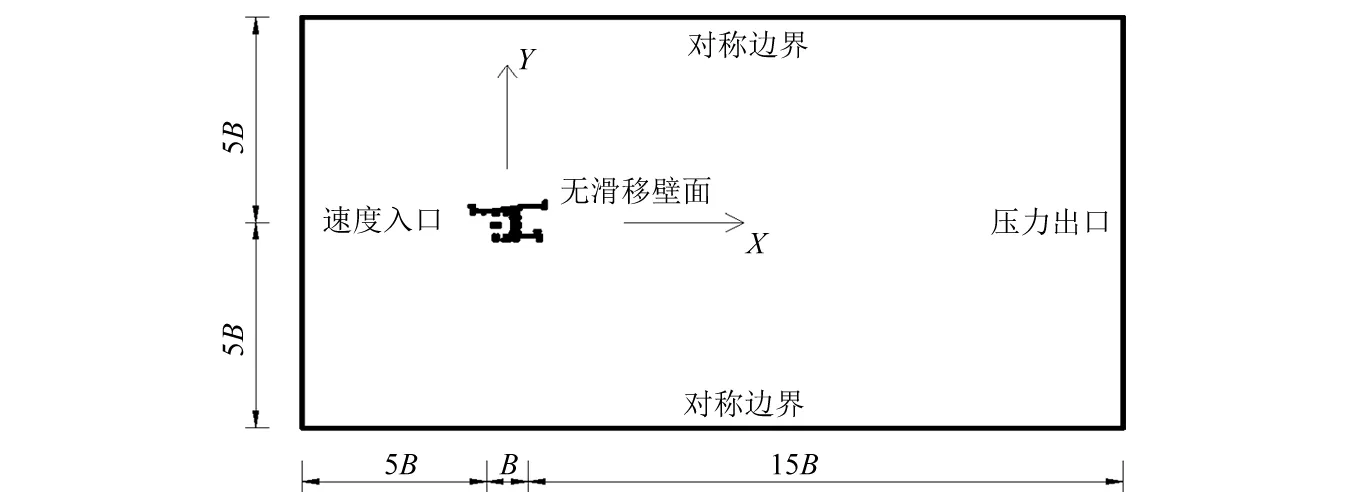
图4 计算域及边界条件Fig.4 Computational domain and boundary conditions

2.2 湍流模型

实际运动流体包含了不同尺度的旋涡，如何模拟实际流体中的湍流是计算流体动力学的重要问题之一。实际流体的湍流模拟主要有三大类方法，即雷诺时均方程(Reynolds Averaged Navier Stokes, RANS)、大涡模拟(Large Eddy Simulation, LES)和直接数值模拟(Direct Numerical Simulation, DNS)。综合考虑计算精度与效率，确定采用RANS中的剪切应力输送模型SSTk-ω湍流模型进行流场模拟，对应的输送方程为

(1)

考虑到本主梁断面形状较为复杂，采用分块化划分方法进行计算域网格划分。图5所示为主梁标准断面网格图，计算域网格总数为226 391。数值模拟求解参数设置见表1。

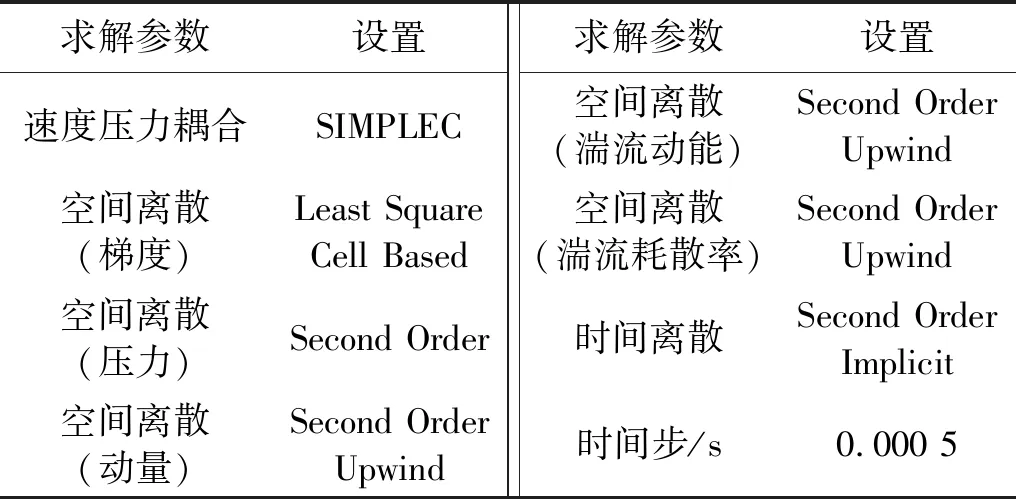
表1 数值模拟求解参数设置

图5 主梁断面附近网格示意图Fig.5 Schematic diagram of the main girder section

2.3 桥面行人风环境模拟结果

桥面行人高度处风速对桥面行人风舒性具有重要影响，采用桥面行人高度处风速与来流风速之比并结合当地气温影响对桥面行人风环境进行评估，桥面行人高度处监测点风速比Ri定义为[12]

Ri=Vi/V0

(3)

式中：Ri为i点处的风速比；Vi为i点人行高度处的平均风速,m/s；V0为来流初始风速,m/s。

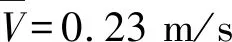
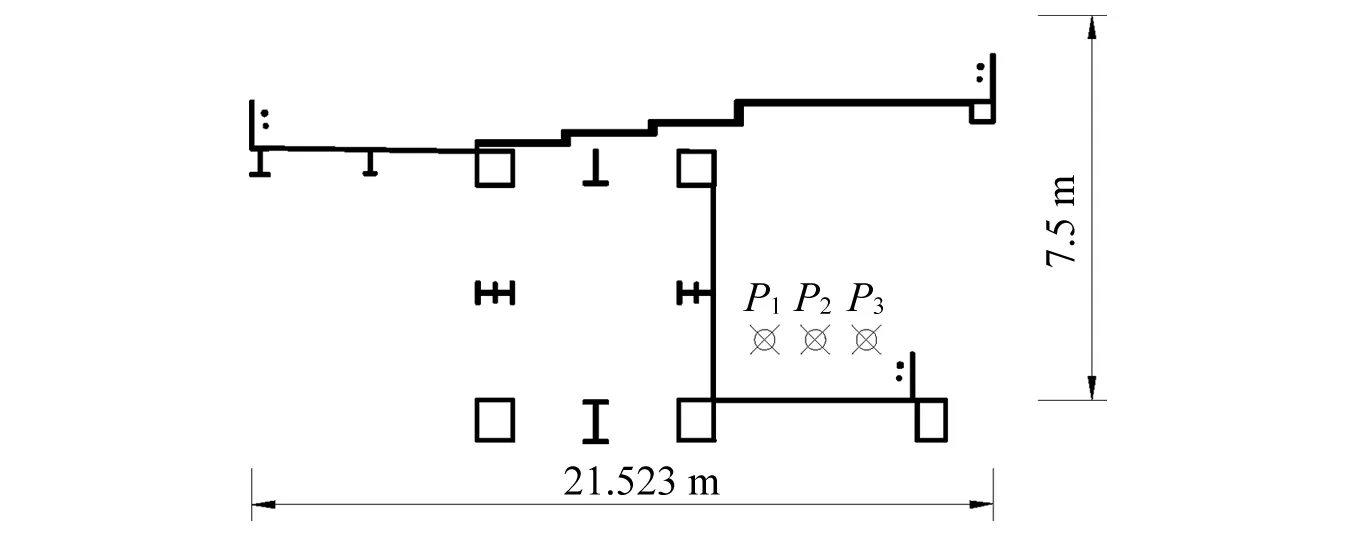
图6 主梁原设计方案风速监测点示意图Fig.6 Wind speed monitoring points of the original main girder

图7 主梁原设计方案各监测点风速时程曲线Fig.7 Wind speed time history curve of monitoring points of the original main girder

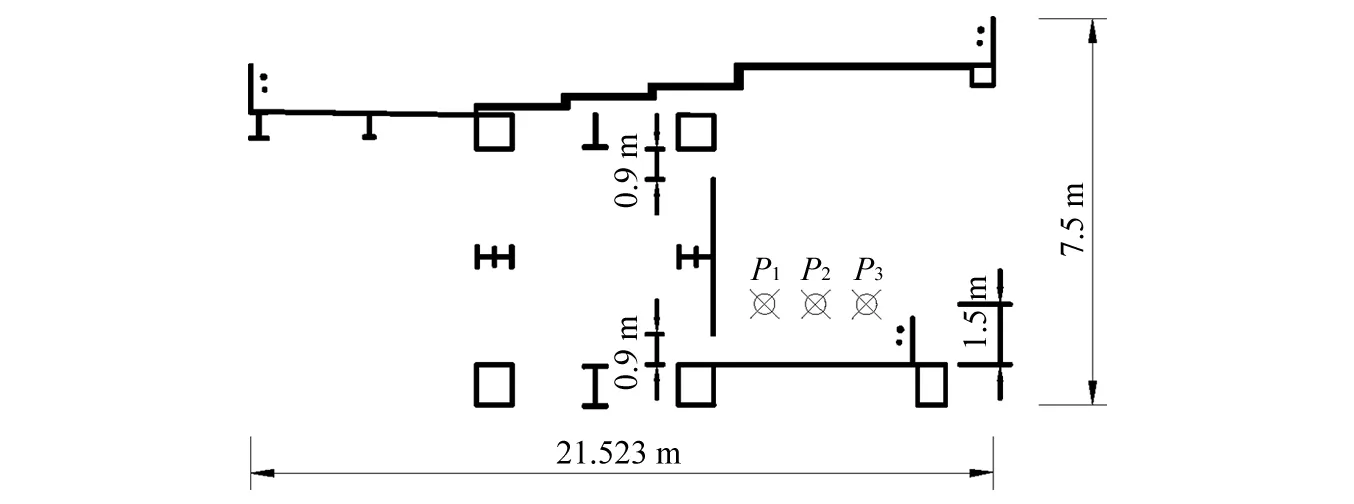
图8 主梁优化断面及风速监测点示意图Fig.8 Wind speed monitoring points of the optimized main girder

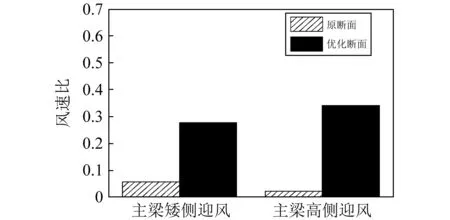
图9 原断面及优化断面风速比结果Fig.9 Wind speed ratio results of the original and optimized main girder separately

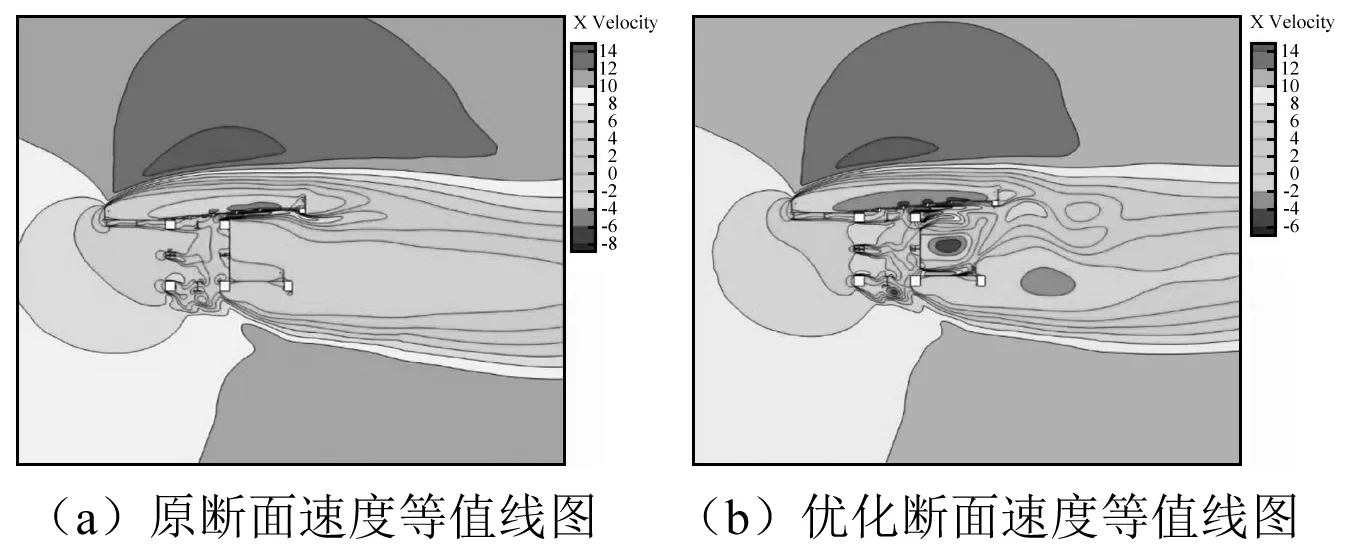
图10 原断面和优化断面主梁附近风速等值线图Fig.10 Wind velocity contours near the original and optimized main girder separately

2.4 气动力系数模拟

主梁断面水平力系数CH、竖向力系数CV以及竖向力矩系数CM定义为

(4)

式中:FH,FV,M分别为横向气动力、竖向气动力以及气动俯仰扭矩；ρ为空气密度；V∞为来流风速；D为主梁断面高度；B为主梁断面宽度；L为节段模型长度[13]。

在0°攻角条件下对主梁断面原设计方案和优化方案分别进行三分力系数CFD数值模拟。图11所示为0°攻角下主梁断面原设计方案和优化方案对应的三分力系数计算结果。由图11可知，主梁原断面优化前后三分力系数总体相差不大。图12所示为主梁断面优化后风分别从左右两侧吹时对应的三分力系数随攻角变化曲线。由图12可知，风从主梁断面不同侧吹时，主梁断面三分力系数相差较大，特别是竖向力系数。

图11 风攻角为0°时主梁断面优化前后三分力系数对比Fig.11 Comparison of force coefficients of the original and optimized main girder separately at 0° wind attack angle

图12 风从不同侧吹时优化后主梁断面三分力系数随攻角变化Fig.12 Force coefficients of the optimized main girder vs. wind attack angles for wind blow from different sides

3 桁架断面人行桥抗风性能风洞试验

3.1 主梁断面涡振性能试验

主桥结构成桥状态动力特性有限元分析结果汇总见表2。由表2可知，主梁断面一阶对称竖弯、一阶对称扭转频率与等效质量分别为0.880 9 Hz，1.813 4 Hz和40.35 t/m，2 750.33 t·m2/m。综合考虑，确定主梁节段模型几何缩尺比为λL=1∶ 50，模型长度L=1.611 m，宽度B=0.441 m，高度为D=0.210 m，模型长宽比L/B=3.65。主梁节段模型试验参数如表3所示。主梁节段模型涡振性能试验照片如图13所示。

表2 主桥结构成桥状态结构动力特性分析结果汇总

表3 主桥结构主梁节段模型试验参数

图13 主梁节段模型风洞试验照片Fig.13 Wind tunnel test photoes of the main girder section model

根据《公路桥梁抗风设计规范：JTG/T D60-01—2004 7.2.6条规定》，该桥涡激共振响应允许根方差值应满足下述规定[14]：竖弯

(5)

扭转

(6)

式中：B为桥面宽度；fb为竖弯振动频率；ft为扭转振动频率。

由式(5)、式(6)计算可得，竖弯涡振允许值[σha]=0.032 m，扭转涡振允许值[σθa]=0.083°。图14所示为高侧迎风时主梁断面竖向和扭转涡激振动响应曲线。由图14可知，当阻尼比较小时(ξv=0.13,ξα=0.28)，风攻角为α=0°,α=±3°时均出现了明显的竖向共振现象，对应实桥锁定区风速分别为Vd=30～40 m/s(0°),Vd=30～36 m/s(+3°)和Vd=30～42 m/s(-3°)，考虑到本桥为了控制人致共振而计划安装TMD(Tuned Mass Damper)阻尼器，故适当将阻尼比增加到(ξv=0.43,ξα=0.33)，对应风攻角为α=0°,α=±3°时竖向和扭转涡激共振得到明显抑制，仅α=-3°在风速为Vd=32～40 m/s时出现了较为明显的竖向涡激共振现象，考虑到该风速已超过本桥设计风速，可不予考虑。

图15所示为矮侧迎风时主梁断面竖向和扭转涡激振动响应曲线。由图15可知，主梁内弧侧迎风状态，风攻角为α=0°时，在实桥风速区间Vd=25～30.7 m/s内主梁发生了明显的竖向涡激共振现象，锁定区最大竖向振动响应根方差为σb=0.012 8<[σha]=0.032 m，满足规范要求；风攻角为α=±3°时，在风速区间Vd=28.3～36.8 m/s内发生了明显的竖向涡激共振，锁定区最大振动响应根方差为σh=0.036 m>[σha]=0.032 m，超过规范允许值，但该锁定区风速区间已超过主梁设计基准风速Vd=28.2 m/s，满足规范要求。主梁内弧侧迎风状态，在各风攻角范围下均未出现明显的扭转涡激共振现象。综上可知，主梁内弧侧迎风状态主梁涡激共振性能满足规范要求。

图16所示为断面矮侧迎风与高侧迎风不同攻角、阻尼比均为ξv=0.43,ξα=0.33时涡振响应根方差比较。由图16(a)可知：0°攻角时，矮侧迎风竖向涡振极值为0.012 8 m；+3°攻角时，矮侧迎风竖向涡振极值为0.035 9 m；-3°攻角时，高侧迎风竖向涡振极值为0.067 6 m。由图16(b)可知：-3°攻角时，高侧迎风扭转涡振极值为0.031 6°，其余攻角下涡振不明显。

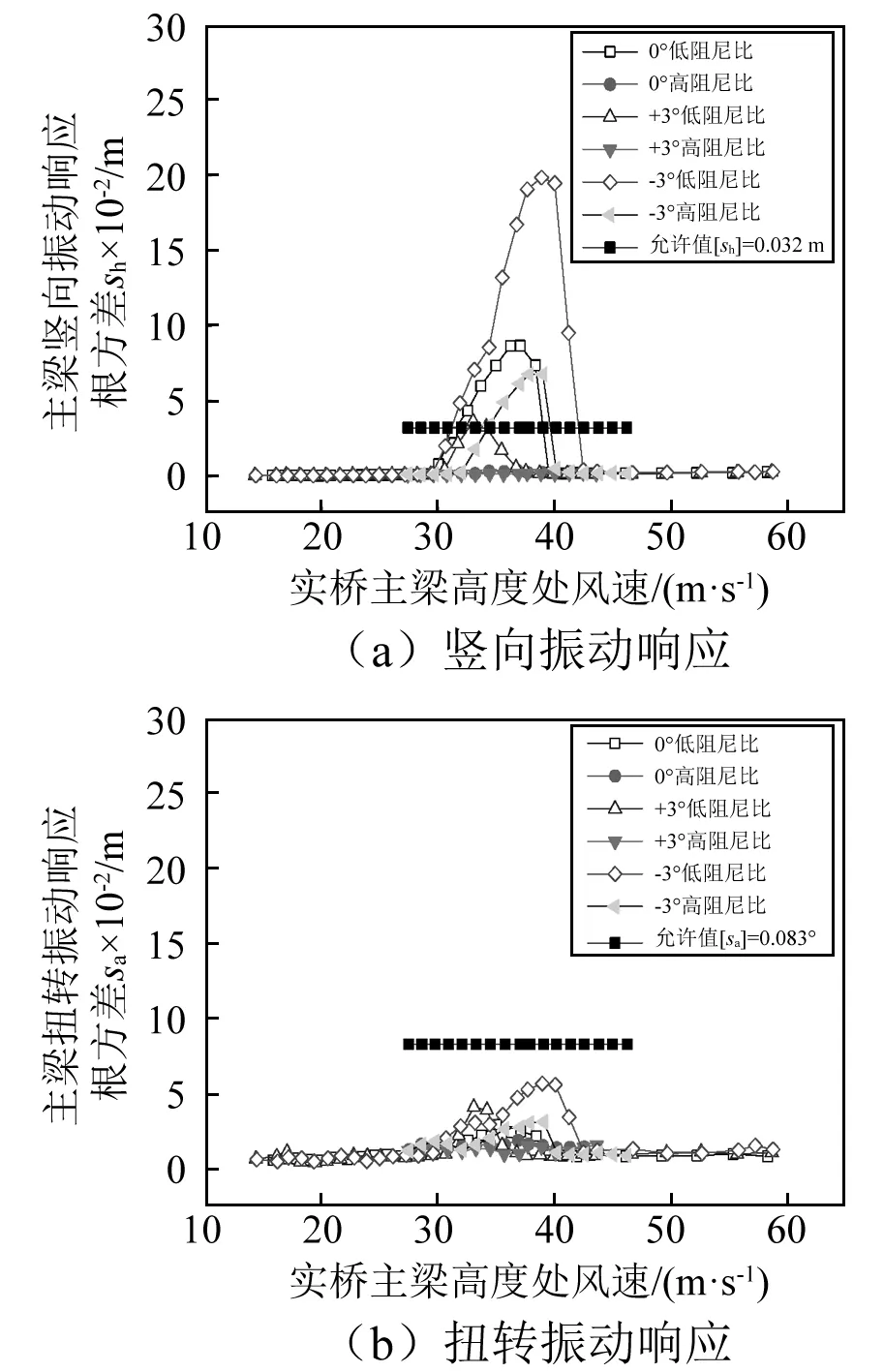
图14 高侧迎风时主梁振动响应根方差随风速变化曲线Fig.14 Wind-induced responses of the main girder under wind blow from high side

图15 矮侧迎风时主梁振动响应根方差随风速变化曲线Fig.15 Wind-induced responses of the main girder under wind blow from low side

图16 高侧迎风与矮侧迎风的振动响应对比图Fig.16 Contrast diagram of main girder vibration under wind blow from high side and low side

3.2 主梁断面颤振性能试验

采用直接试验法对主梁断面矮侧迎风和高侧迎风两种状态进行了颤振稳定性试验，试验参数见表3。试验风攻角为-3°，0°，+3°。试验测试风速进行至V=10 m/s，均未观察到颤振现象。具体试验结果见表4，由表4可知，主梁断面矮侧迎风和主梁断面高侧迎风两种状态均满足颤振稳定性要求。

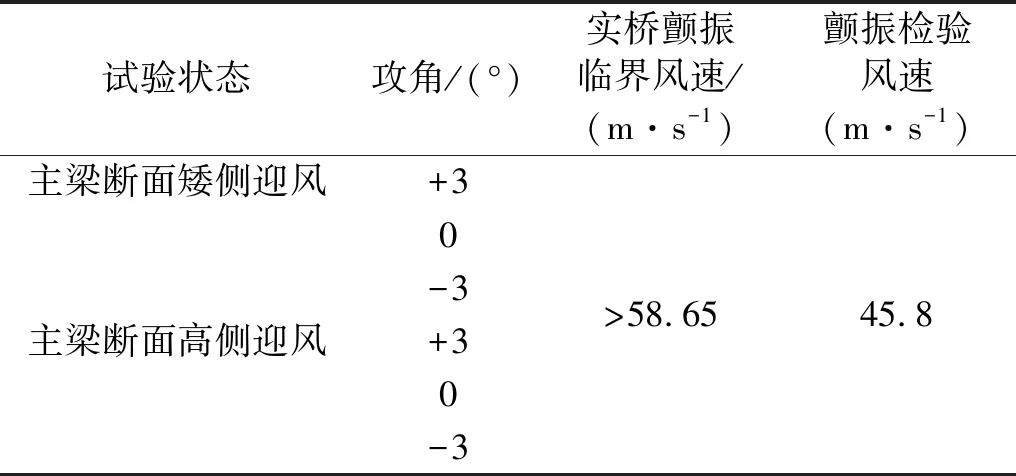
表4 主梁节段模型颤振性能试验结果

3.3 主梁断面测力试验结果

主梁测力试验模型几何参数与测振试验一致，试验来流风速为V∞=10 m/s，图17为三分力系数试验照片。图18所示为主梁断面高侧、矮侧迎风状态对应的主梁断面三分力系数随攻角变化曲线，图中三分力系数定义见式(4)。由图18可知，风分别从主梁断面矮侧和高侧吹时，主梁断面三分力系数存在明显的差异，其中竖向力系数差异较大；主梁断面三分力系数CFD计算结果与试验结果总体较为吻合。

图17 三分力系数试验照片Fig.17 Test photo of aerodynamic coefficients

图18 主梁断面优化后的三分力系数试验与数值模拟结果Fig.18 Experimental and numerical results of static coefficients of the optimized main girder

4 结 论

采用CFD数值模拟和风洞试验相结合的方法对某钢桁架曲线人行桥的桥面风环境和抗风性能进行了研究，得到如下主要研究结论：

(1)桁架内文化墙对钢桁架下侧桥面行人风环境影响较大，适当增加文化墙与上下弦杆之间间隙可有效改善钢桁架下侧桥面行人风环境。

(2)对于设置了纵向文化墙等挡风附属设施的不对称桁架人行桥，主梁断面矮侧迎风与高侧迎风状态均产生了涡激共振现象。且高侧迎风时涡激共振现象更为显著，而适当增大桥梁结构阻尼可有效抑制。

(3)不对称钢桁架曲线人行桥矮侧、高侧迎风时三分力系数存在明显的差异。0°攻角下，矮侧迎风时水平力系数CH=1.444,竖向力系数CV=0.880 4，竖向力矩系数CM=0.221；高侧迎风时水平力系数CH=1.515，竖向力系数CV=0.055 8，竖向力矩系数CM=0.032 6。