基于SPH-FEM耦合法的射流冲击型动量定律实验装置误差特性分析

杨 嵩， 朱先勇， 王 辉， 于 萍

(吉林大学 机械科学与工程学院，长春 130025)

射流冲击是自然界中广泛存在的一种自然现象，波浪对礁石及船体的冲击等都可以理解为射流冲击[1]。射流冲击同时也具备广泛的工程应用背景，从19世纪首次应用于矿物开采到如今广泛应用于航空、建筑、化工、机械加工、医药等领域，如利用液体射流冲击进行表面清洗、金属切割、岩石破碎等[2]；射流冲击在给工业界带来便利的同时也引发出一系列的问题，如液滴冲击高速旋转的涡轮叶片引发叶片表面磨损及损伤，雨滴对高速飞行器表面蒙皮产生的破坏[3]。因此有必要将射流冲击尤其是水射流冲击的研究引入到流体力学的日常教学中。动量定律是流体力学基本定律，作为射流冲击现象的基本原理，有广泛而深刻的理论及实践应用意义[4]。利用水射流冲击固体方法对动量定律进行验证也是流体力学实验教学中常基本方法。

水射流冲击固体是一个涉及水锤力、冲击力(滞止压力)、材料变形、损伤等诸多因素的非线性动力学过程，具有大变形、高应变率、瞬态过程难于观察和检测等特点[5]。国内外学者分别对水射流冲击过程和动量定律实验装置进行了理论和应用研究。Field从理论、实验和应用三个方面对液体冲击引发的侵蚀损伤进行了研究，Obara等利用高速相机对高速水射流冲击PMMA(Polymethyl Methacrylate)样件过程中射流冲击波的形成、界面反射及PMMA的损伤进行了研究，重庆大学煤矿灾害动力学与控制国家重点实验室对使用脉冲水射流破岩问题进行了深入的研究[5-6]；廖华林等[7-9]对高压射流冲击岩石过程中涉及的流-固耦合作用、岩石破碎机理及在石油工程中的应用进行了研究。国内对动量定律实验的研究多从动量方程本身入手，通过理论计算及实测等方法讨论动量系数等对测量精度的影响并提出解决方法，如丁彤[10]对影响动量定律实验精度的参数进行了灵敏度分析，提出解决办法并开发了验证样机；刘银庆等[11]对动量定律验证仪测量部分进行改进，有效减小了紊流、弹簧异常波动对精度的影响；胡卫红等[12]和陈国玉[13]分别设计了一种新式动量定律验证仪。

作为以射流冲击现象为基础的动量定律实验装置，射流冲击的引入有助于提升动量定律实验装置工作特性分析的可信度、准确性，也便于在日常的动量实验教学中更好的向学生阐明射流冲击原理、过程及实验误差产生的原因。

综上，本文将以吉林大学实验教学所用射流冲击型动量定律实验装置为研究对象，本装置为平板射流冲击式，射流冲击到平板上，通过测定平板所承受的冲击力来验证动量定律。本文拟采用SPH-FEM(Smoothing Particle Hydrodynamics, SPH )耦合算法模拟射流冲击平板过程，分析平板、传感器结构在射流冲击载荷作用下的响应特性，结合分析结果展开误差讨论。

1 射流冲击型动量定律实验装置结构

射流冲击型动量定律实验装置由如下部分组成：①水箱；②动力装置(泵-电机模块)；③流量计量装置；④射流发生器；⑤圆形平板；⑥底座；⑦检测装置(传感器和数显表)，具体如图1(a)所示。射流冲击过程所涉及的结构如图1(b)所示，其中包含圆形平板、电阻式应变传感器、底座及若干连接件；圆形平板通过中心孔与传感器固连，传感器通过螺栓与底座固连，底座通过粘胶与实验装置基体固连。圆形平板和传感器是核心组件，圆形平板用于改变射流动量形成射流冲击力，传感器用于传递、测量射流冲击力的大小。

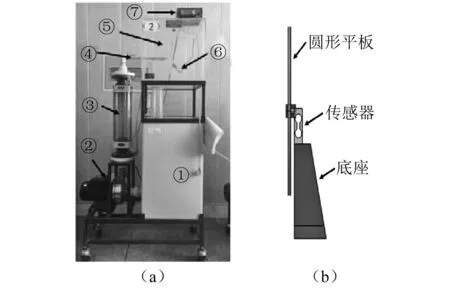
图1 射流冲击测试装置结构图Fig.1 The structure graph of jet impact test apparatus

2 SPH-FEM耦合算法

水射流冲击固体结构的过程是一个典型的流-固耦合问题，其中涉及流体的大变形，如果采用传统的拉格朗日法计算水射流冲击，容易出现网格畸形等错误从而导致计算困难甚至终止[14]。本文采用SPH-FEM耦合算法对水射流冲击过程进行模拟，此算法由SPH算法和FEM算法两部分组成，水射流用SPH算法模拟，固体结构采用FEM方法模拟，充分考虑水射流与被冲击结构之间的作用关系。SPH算法是一种无网格方法，在处理材料大变形、不连续介质动力学问题上优势明显，广泛应用于大变形冲击动力学问题的求解，但SPH算法在求解材料小变形问题的求解精度及计算效率均逊于传统有限单元法。因此可以将SPH算法与FEM(Finite Element Method)算法结合，充分利用两种算法的优势，求解大变形、冲击、小变形等共存耦合问题[15]。

2.1 SPH计算理论

SPH的全称为光滑粒子流体动力学方法，SPH方法是一种无网格、纯拉格朗日方法，其最初被应用于天体物理领域并取得成功。1994年Monaghan首次将SPH方法应用于自由表面流动模拟，随后SPH方法被广泛的应用于水力学、冲击碰撞、自由表面流动等相关的学科研究中[16-19]。

SPH算法的基本逻辑是用一系列任意分布的粒子来代替连续介质流体，通过粒子集合和插值核函数来估算N-S方程的空间函数及其导数实现基本方程→计算公式的转化，将原来同时含有时间和空间导数的偏微分方程转化成只含有时间导数的方程。SPH方法的基础是核函数，通过对核函数的积分场函数近似，其表达式如式(1)所示，在此基础上应用粒子对核近似方程进行再近似，通过应用局部区域内相邻粒子对应的值来叠加和取代函数及其导数积分形式，称为粒子近似，如式(2)。从而实现流体力学方程的粒子近似过程[20-21]。

(1)

(2)

式中：f为场函数；Ω为计算区域；x为坐标向量;h为光滑长度；W为核函数；ρ为密度；m为质量。

将SPH法应用于N-S方程，具体如下：质量守恒方程(式(3))，动量守恒方程(式(4))，能量守恒方程(式(5))。

(3)

(4)

(5)

SPH算法处理液-固冲击问题的优点在于对流项直接通过粒子的运动来模拟，完全消除了自由界面上的数值发散问题，保证了自由界面追踪的清晰准确；无网格特性同时避免了网格扭曲及重构带来的问题。

2.2 SPH-FEM耦合处理

SPH与FEM的耦合是通过接触罚函数的方法将质点的力作用于有限元单元表面。接触类型为点-面接触，SPH粒子为从节点，FEM单元为接触主面，在每个时间步内均需要检查SPH粒子与有限单元表面的穿透状态，如果存在穿透则应用罚函数，如果无穿透则不进行任何处理。

3 计算模型描述

结合实验台使用实际，本文拟分析射流射速为17.7 m/s条件下的冲击过程；射流发生器产生直径为8 mm的水射流；射流冲击位置为平板中心，靶距为2 mm，忽略重力；冲击作用时间设定为30 ms。

实验装置的计算模型如图2所示。模型中各部分的材料、单元属性如表1所示。材料PMMA和STEEL的基本属性[22]如表2所示，射流(WATER)状态方程EOS选择US-UP，具体参数如表2所示。依据实验条件，经计算可知，射流冲击力小于20 N，结构所属材料PMMA和STEEL均处于弹性变形区，无塑性变形。

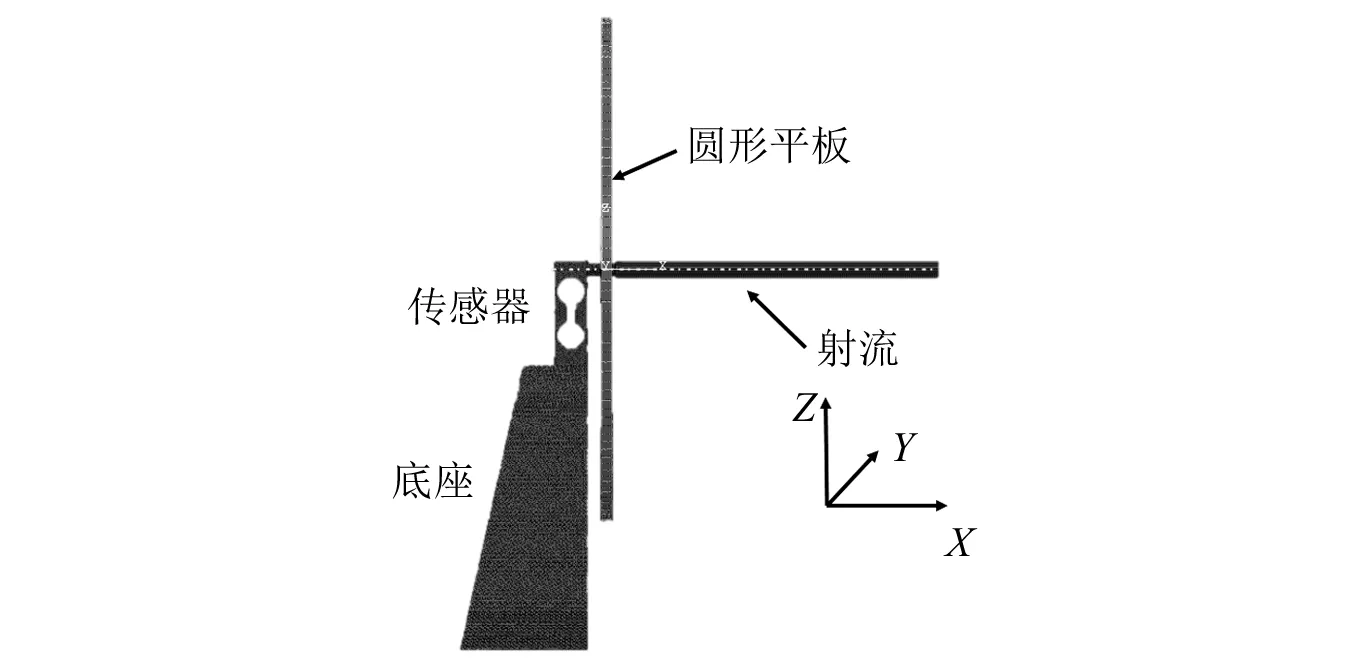
图2 射流冲击计算模型图Fig.2 The numerical simulation graph of jet impact model

编号名称材料单元类型单元尺寸/mm1底座PMMASOLID22传感器STEELSOLID13圆形平板PMMASOLID54射流WaterParticle1

表2 PMMA，STEEL，WATER材料属性Tab.2 The properties of material PMMA STEEL and WATER

4 结构位移响应特性分析

结构响应特性分析主要分析传感器及平板结构在射流冲击作用下的位移响应，目的在于还原射流冲击过程中平板及传感器的运动过程，为误差分析提供参考。

4.1 传感器位移响应特性

计算模型中可以将传感器结构简化为悬臂梁模型，悬臂梁自由端承载。为简化描述，结合传感器应变片粘贴位置，在传感器结构侧面取5个测量点A，B，C，D，E，利用测量点间接描述传感器结构的响应，A～E位于一条直线上，具体位置如图3所示。

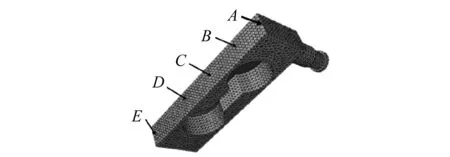
图3 传感器测量点位置分布图Fig.3 The distribution graph of observation points on sensor

A～E测量点在X，Y，Z方向的位移变化如图4～图6所示。由图4和图5可知，在X方向(射流冲击方向)和Y方向上，A～E点发生了移动且运动趋势保持一致。A点位移幅值SA最大，E点位移幅值SE最小，B，C，D点位移幅值介于A，E之间，这表明传感器在X，Y方向上受力并产生了弯曲变形；但传感器在X，Y方向的具体形变过程及变形幅度略有不同。

由图4可知，传感器在X方向受到射流冲击力作用产生移动和变形，A～E点的位移曲线经过振荡调整后在t=8 ms时趋于稳定，这表明传感器在X方向的位移和变形在经历振荡调整后于t=8 ms时趋于稳定，传感器在X方向的受力Fsx趋于稳定。

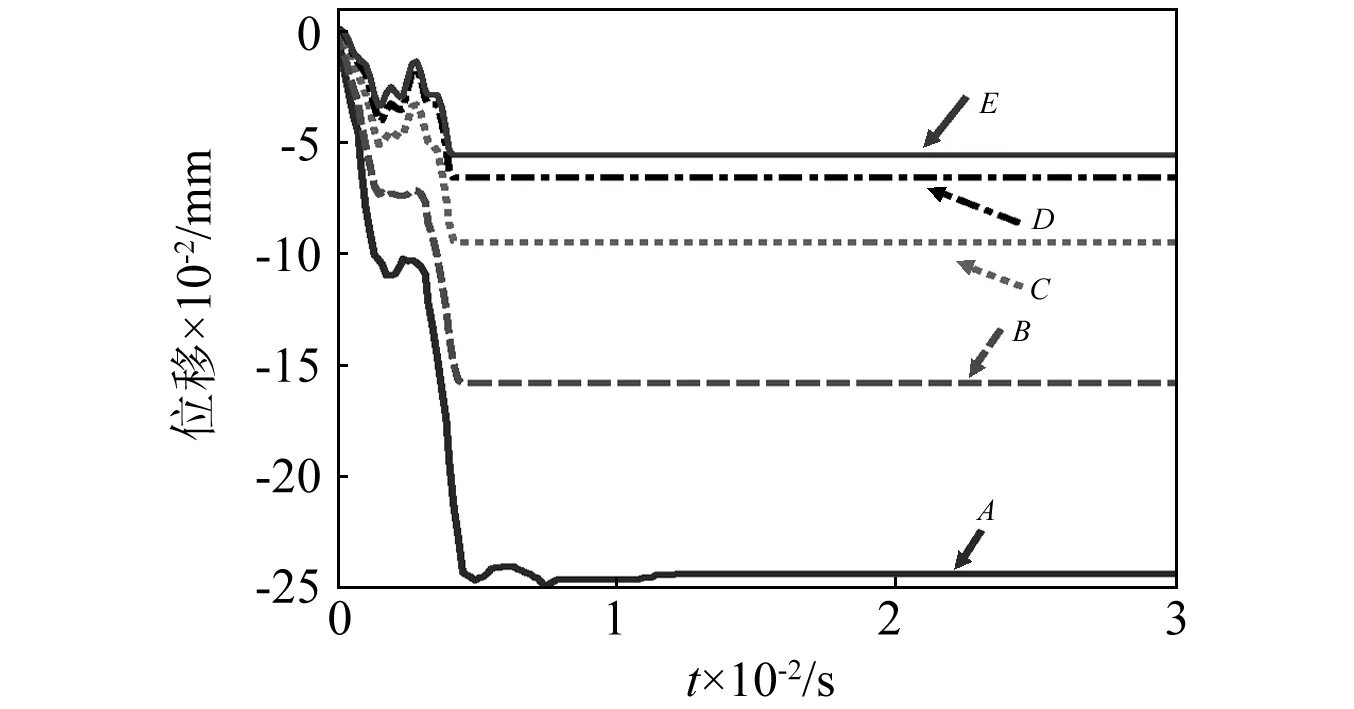
图4 传感器测量点在X方向位移变化图Fig.4 The displacement graph of sensor observation points with time on direction of X

由图5可知，传感器在Y方向受到外力作用产生移动和变形，A～E在Y方向的位移曲线持续振荡无稳定趋势，但呈一定周期性。这表明传感器在Y方向的位移和变形持续变化，传感器在Y方向受力Fsy非恒定且保持振荡。对比X，Y方向上A～E点的位移差值可知，X方向上A～E的位移差值大于Y方向上A～E的位移差值，即传感器在X方向的变形大于Y方向变形，这表明传感器在X方向所受外力Fsx大于Y方向所受外力Fsy。

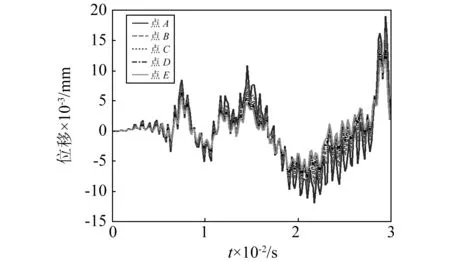
图5 传感器测量点在Y方向位移变化图Fig.5 The displacement graph of sensor observation points with time on direction of Y

由图6可知，A～E点在Z方向上发生运动，位移曲线持续振荡，A～E点Z方向的位移变化规律与X,Y方向略有不同，B,E两点的位移幅值最大、方向相反，C,D两点次之、方向相反，A点位移最小，造成此种情况的原因有如下两个：①传感器在X,Y方向的变形间接引起Z方向位移变化;②传感器受到了不规则的弯、扭作用,Z方向的位移变化值远小于其他两个方向。

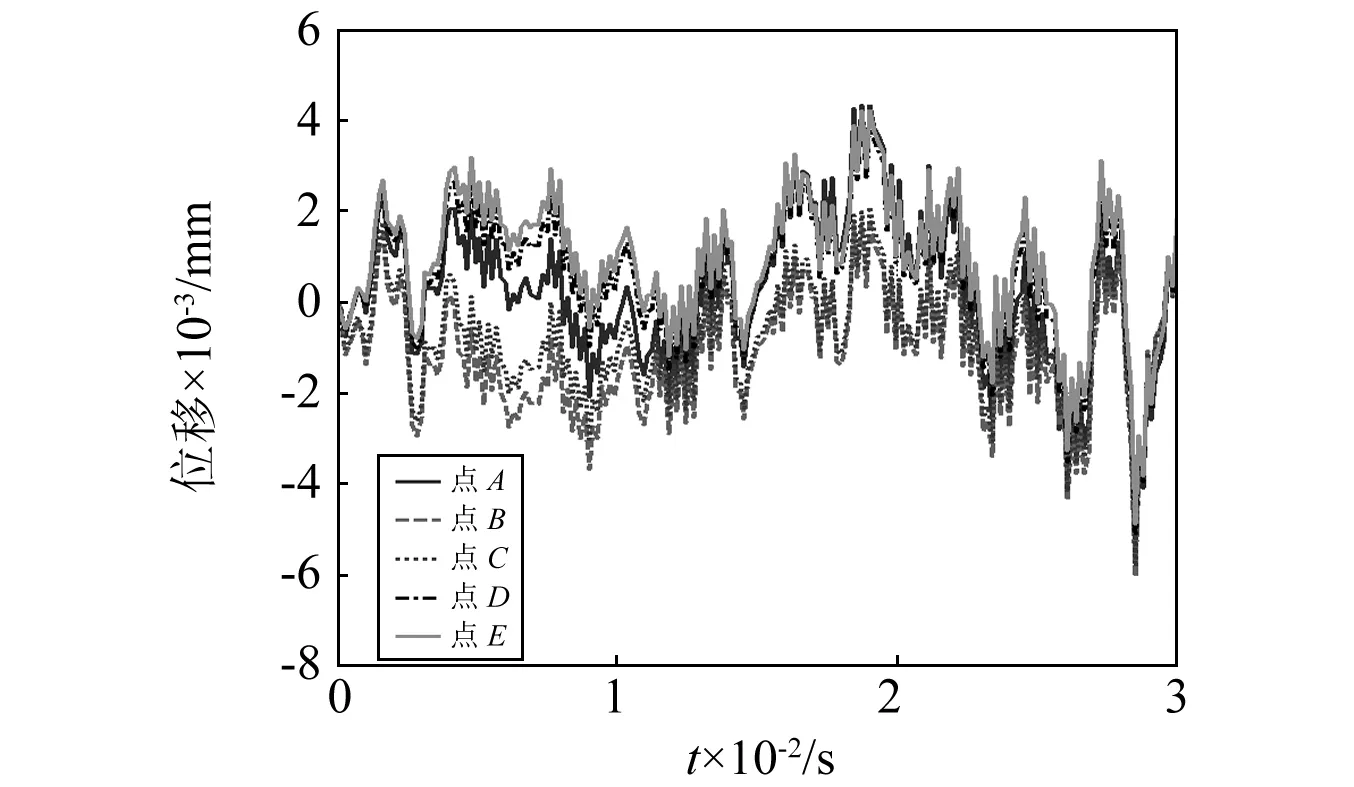
图6 传感器测量点在Z方向位移变化图Fig.6 The displacement graph of sensor observation points with time on direction of Z

通过对传感器位移响应特性的分析可知，在射流冲击力的作用下，传感器在射流方向(X方向)发生移动，经振荡调整后趋于稳定，传感器在Y，Z方向由于受到非恒定外力的作用而持续振动，Y方向的振动类似于弯曲，Z方向振动为不规则振动，Y方向的振荡幅度大于Z方向，Z方向的振荡频率大于Y方向。Y，Z两方向上的不规则振动会对冲击力的测量带来误差。

4.2 平板位移响应特性

计算模型中，平板在射流冲击作用下的位移响应云图如图7所示。在射流冲击瞬间，平板中心区域在冲击力的作用下沿射流冲击方向发生移动，由于惯性作用平板的位移分布同几何结构一致，呈同心圆形式，中心位置位移量最大，最外侧位移最小，径向位置相同区域的位移保持一致，此时平板发生凹变形，如图7(a)所示。随着冲击的持续，平板各点位移量均增加，但分布规律保持不变，仍为同心圆，位移分布关于Y，Z轴对称，平板发生凹变形，如图7(b)所示。

图7 平板位移变化图Fig.7 The displacement graph of plate with time

随着冲击的进一步作用，平板各点位移量继续增加，但分布规律发生了变化，由同心圆形式转化成仅沿Z轴对称，最大位移区域由平板的中心位置沿Z+方向逐渐上移直至顶端，位移分布由圆形变为带条状，以中心孔为界，Z-方向的位移小于等径向位置Z+方向的位移，这表明平板发生倾斜并产生弯曲变形，如图7(c)～图7(g)所示。t=10 ms以后，平板的位移趋于稳定但依旧存在小幅振荡波动，此时平板的位移分布规律与之前不同，最大位移区位于平板的中上段，呈带条状分布，平板下半部分的最小位移区与最大位移区关于中心孔呈对称分布，平板位移量的径向不一致表明平板发生较严重的不规则弯曲变形。

通过对射流冲击过程中平板位移响应特性进行分析可知，在射流冲击作用下，平板中心首先沿射流方向发生移动并带动其他区域运动，随着射流冲击的持续作用，平板的运动由沿射流方向的运动和不规则的摆动两部分组成， 沿射流方向的运动经振荡调整后趋于稳定，而不规则的摆动会持续存在。平板的不规则摆动作为一个附加载荷作用在与之相连接的传感器上，进而产生一个冲击力测量误差。

5 传感器应力特性分析

传感器应力特性主要分析传感器结构的应力响应特性，尤其是A～E测量点的应力响应特性。

当射流与圆形平板接触的瞬间，射流动量发生突变，形成一个类脉冲冲击力，平板中心部分沿射流方向发生移动，平板与传感器的接触，产生一个接触应力，在射流冲击力作用下，传感器发生弯曲产生弯曲应力，如图8(a)所示。随着射流冲击的持续，传感器弯曲变形增加，传感器内部弯曲应力增加，传感器中心的薄壁结构处为一个弯曲应力集中区，中心薄壁结构抗弯截面系数小是产生应力集中的主要原因，如图8(b)和图8(c)所示。

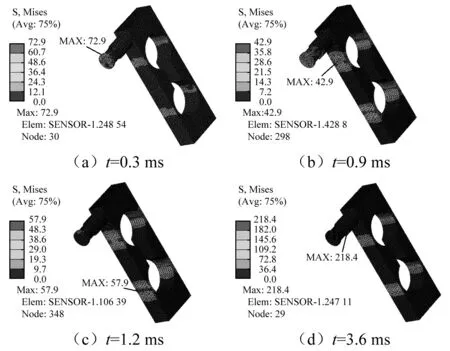
图8 冲击过程中传感器Mises应力分布图Fig.8 The Mises contour of sensor in impacting process with time

对比图8(a)和图8(d)可发现，传感器结构存在另外一个应力集中区域，即传感器与平板的连接处。由上文分析可知，在射流冲击作用下，平板存在不规则摆动，平板和传感器之间会产生接触应力，且最大接触应力点非固定。

传感器测量点A～E的Mises应力变化曲线如图9所示。由图9可知，A～E测量点的Mises应力持续振荡变化，Mises应力的变化趋势与位移变化趋势相对应；C点的Mises应力最大，因为C点位于抗弯截面系数较小的中心薄壁位置，A，B两点的Mises应力较小，因为A，B两点更靠近悬臂梁结构的自由端，D，E两点的Mises应力介于中间，因为D，E两点位于抗弯截面系数较大的固定端。

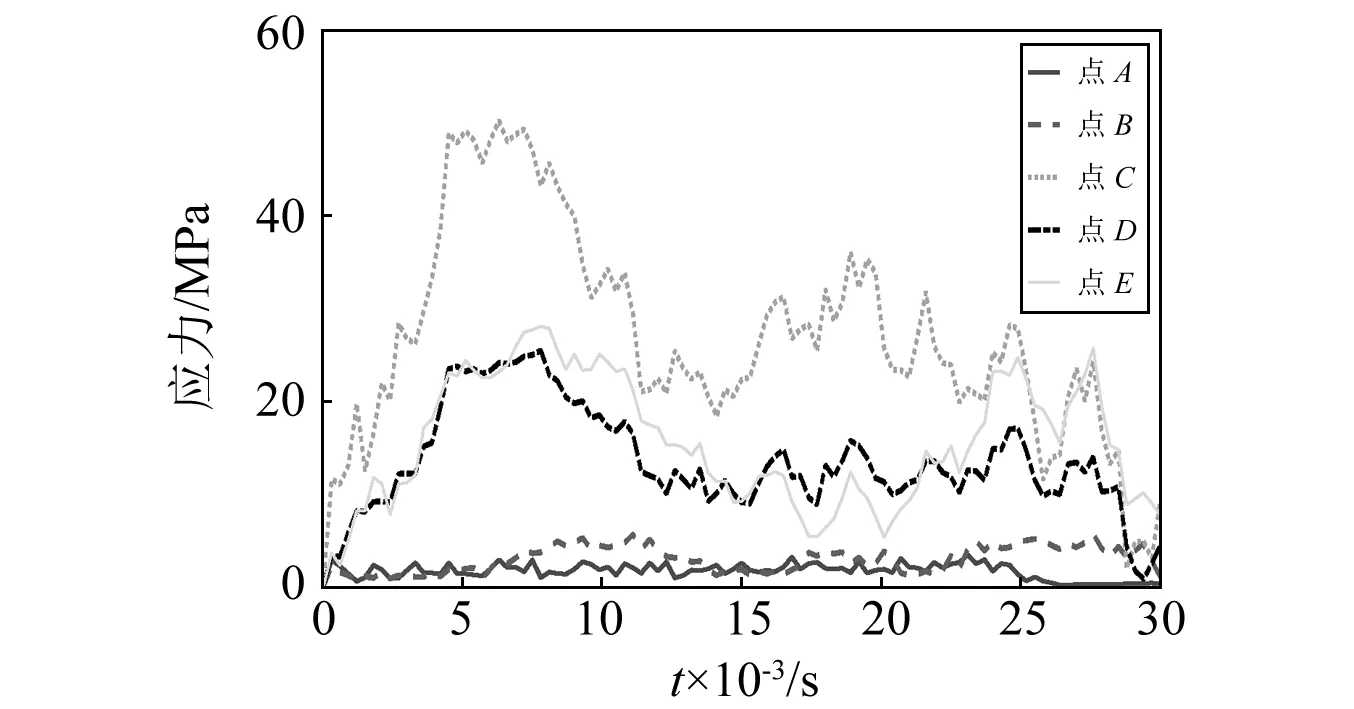
图9 传感器测量点Mises应力变化图Fig.9 The Mises stress graph of sensor observation points with time

选取测量点C为研究对象，对其σx,σy,σz,σxy,σxz,σyz变化情况进行研究，具体如图10所示。

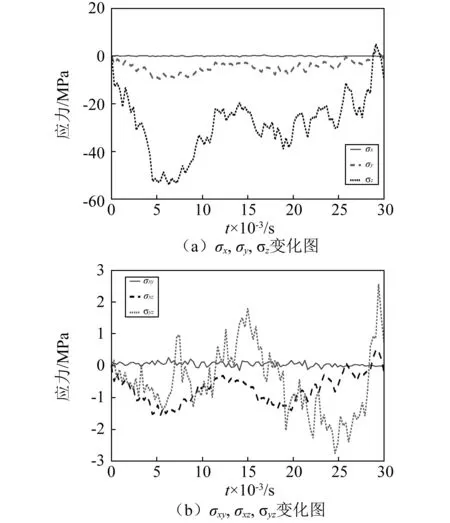
图10 传感器测量点C应力变化图Fig.10 The stress graph of sensor observation point C with time

由图10(a)和图10(b)可知，传感器C测量点同时存在拉/压应力和剪应力，即传感器同时承受弯曲和扭转作用，且弯曲和扭转作用是振荡变化的，这与上文位移响应分析结果相对应。

综上可知，射流冲击过程中，射流对平板和传感器的作用力为非恒定的振荡变化量；在此外力作用下，平板和传感器发生不规则的摆振运动。在射流冲击力作用下，传感器承受弯、扭联合作用，传感器内部同时存在弯曲和剪切两种应力。

6 传感器测量误差分析

由上文分析可知，射流冲击载荷作用下，平板和传感器会产生不规则振动。电阻式应变传感器作为测量元件，其不规则振动会导致传感器产生横向变形，依据应变传感器的横向效应理论，横向变形会引起测量误差[23]。由电阻式应变传感器的测量原理可知，传感器应变片的弹性变形量s与冲击力F存在映射关系，即F=f(s)，因此可通过传感器应变片的弹性形变量s来间接表征射流冲击力F。

结合传感器的布置形式及上文分析，利用A～E测量点相对位移来表示应变片的形变量。E点位于固定端，E点的相对位移为0，其他点的相对位移以E点为参考；Z方向的位移变化较小，此处不予考虑。传感器在X和Y方向相对位移及变形如图11～图13所示。

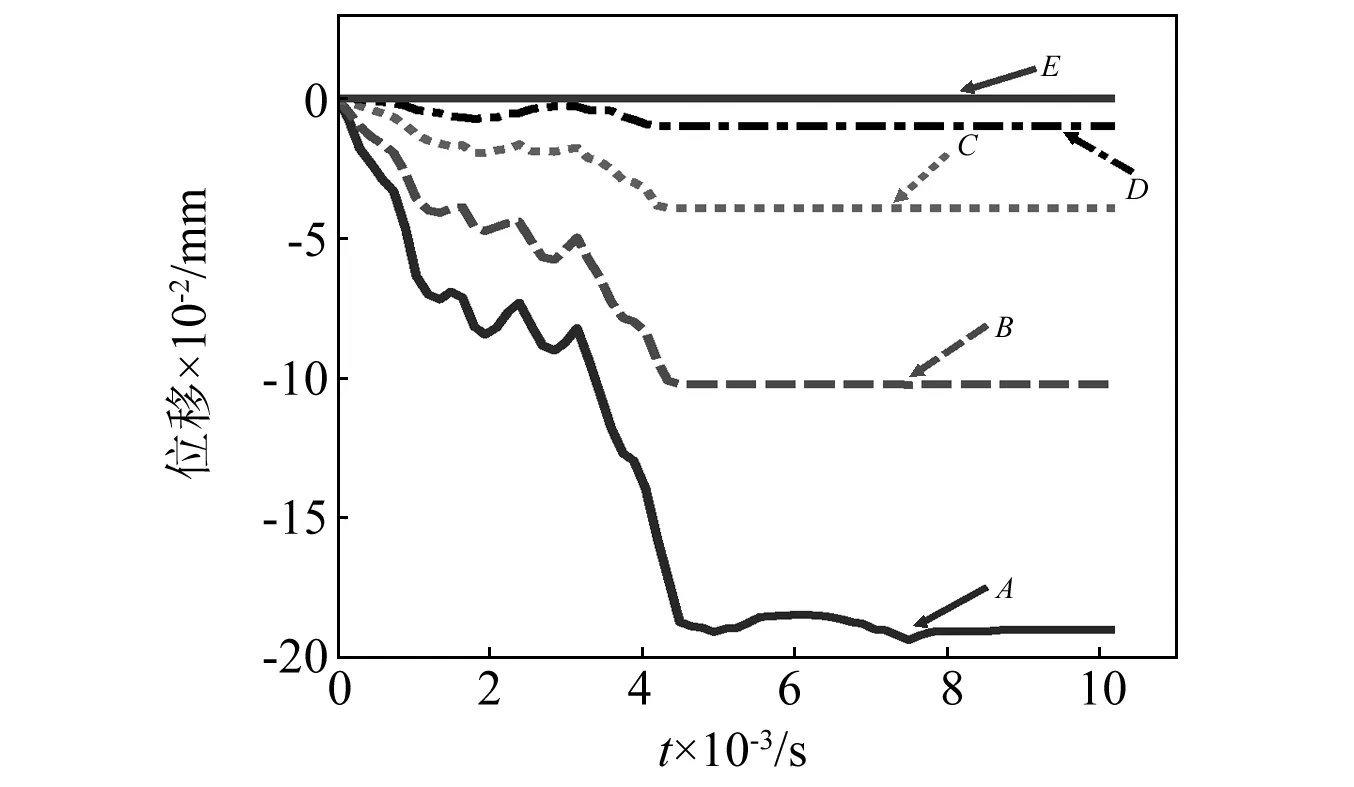
图11 传感器测量点X方向相对位移变化图Fig.11 The relative displacement graph of sensor observation points with time on direction of X

由图11可知，在射流冲击作用下，传感器在X方向产生运动经振荡调整后趋于稳定，A，B两测量点的相对位移变化曲线并不平滑，存在突变，此突变由圆形平板运动调整造成，由于A点更接近自由端，A的变化量更大。

由图12可知，传感器在射流冲击力的作用下，在Y方向进行往复振荡运动，A～E的振荡频率相同、振幅依次逐渐降低，振荡周期随冲击作用时长逐渐增加。

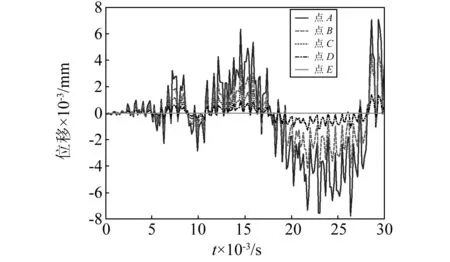
图12 传感器测量点Y方向相对位移变化图Fig.12 The relative displacement graph of sensor observation points with time on direction of Y

以A～E测点相对位移数据为基础对传感器主体部分在X，Y方向上随时间的变形进行3D拟合，如图13所示。

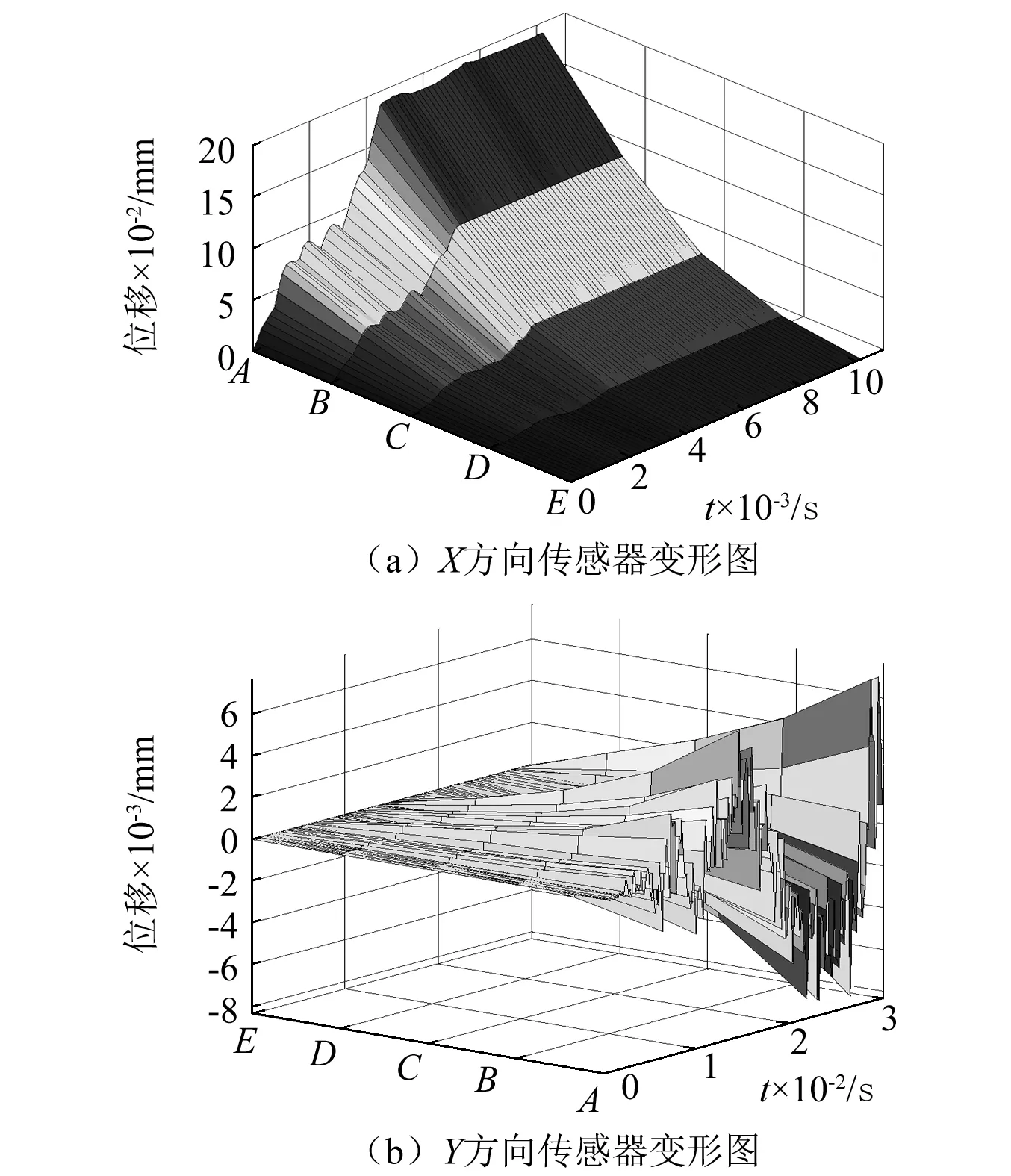
图13 传感器变形图Fig.13 The deformation graph of sensor with time

由以上分析可对射流冲击作用下传感器所测冲击力的数值做如下推测，即传感器所测定冲击力的值应该按照c(t)+Asin(wt+φ)规律进行变化。c(t)由传感器应变片在X方向的变形决定，经过振荡调整后为一个稳定值；Asin(wt+φ)主要由应变片在Y方向的变形决定，A，w，φ为变量，将A/c定义为位移响应比。若以测量点C的相对位移来表征传感器的测量误差变化，考虑应变传感器横向效应引发的测量误差。由电阻应变式传感器的测量原理可知，应变片在二向应变场下的响应为

(6)

式中：R为电阻值；Sx为纵向灵敏度；Sy为横向灵敏度；Sα为剪切灵敏度；εx为纵向应变；εy为横向应变；εα为剪切应变。

一般情况下剪切灵敏度较小，可以忽略。此时式(6)变为

(7)

式中：k=Sy/Sx为横向灵敏度系数，此处可假定εy=-μ1εx，μ1为传感器结构材料的泊松比。对式(7)进行变换可得

(8)

式中:Sg为厂家测定的灵敏度系数，对比式(7)和式(8)可得

Sg=Sx(1-μ1k)

(9)

综合式(7)～式(9)可得

(10)

经变换可得

(11)

如果传感器仅考虑应变片的灵敏度系数，则有

(12)

(13)

传感器横向效应所引发的误差为

(14)

若选取传感器测量点C在Y方向上相对E点的位移作为横向效应的边界值。此时可认为，测量过程中Y和X方向上的位移响应比的绝对值|A/c|与应变比εy/εx相等，即εy/εx∈[0%,7%]。传感器结构材料的泊松比为0.3，即μ1=0.3，对k取不同值，可估算出传感器的测量误差如表3所示。由表3可知，传感器横向效应所引发的测量误差与横向灵敏度系数k、应变比εy/εx有关，传感器的横向灵敏度系数可以认为是传感器的固有特性参数，此时传感器的测量误差是一个关于应变比εy/εx的一次函数，依据式(14)可知，εy/εx越大，传感器横向效应所引发的测量误差越大。

表3 传感器误差估算表Tab.3 Sensor estimated error

依据仿真参数对动量定律实验装置进行实测，测试数据如表4所示，实测冲击力的误差范围小于1%，与依据式(14)估算的误差(见表3)相近，此结果表明，文中所采用的测量误差估算方法针对此问题有效。造成估算误差与实测误差之间差异的原因如下：

① 传感器内部存在误差补偿；

② 温度、湿度等引起的传感器测量误差；

③C点的位移响应不能完全反应应变片的真实变化；

④ 实测过程中水泵流量脉动引发的射流速度变化；

⑤ 计算模型、材料属性等与真实系统之间的差异。

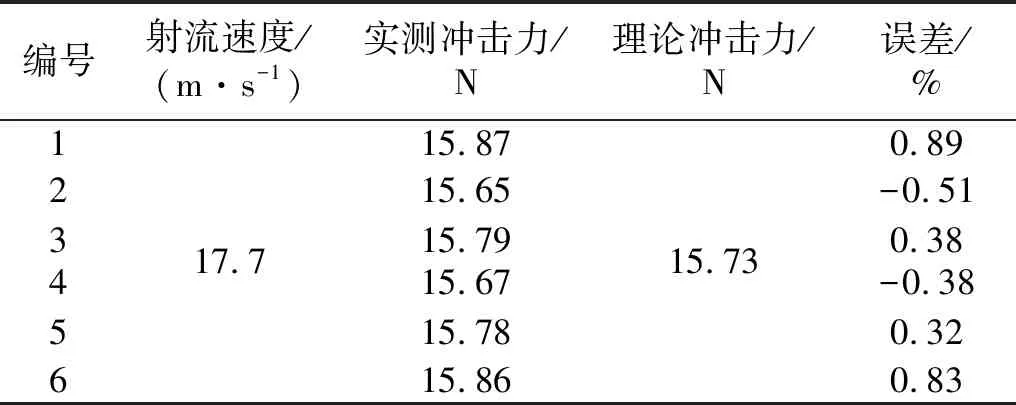
表4 实验误差表Tab.4 Experiment error

7 结 论

本文以射流冲击型动量定律实验装置为研究对象，采用SPH-FEM方法分析了射流冲击载荷作用下，圆形平板及传感器结构的位移响应特性和传感器的应力特性，以此为基础对传感器测量误差产生的原因及误差范围进行了分析、计算，并与实测实验结果进行对比，验证分析、计算方法的可靠性。综合以上分析获得如下结论：

(1)射流冲击型动量定律实验装置在工作过程中，圆形平板及传感器结构在非射流冲击方向上会发生持续不断的不规则振动，此不规则振动引发传感器产生测量误差。

(2)应变电阻的横向理论可用于应变传感器的测量误差估计。

(3)不规则振动引发的测量误差的大小与传感器位移响应比(应变比)呈线性函数关系，位移响应比越大，测量误差越大。

(4)射流冲击力的测量值由固定值和变化值两部分组成，固定值主要由传感器在射流冲击方向的变形决定，变化值由传感器在其他方向上振动引发的变形决定。

本文所采用的分析方法及所获得的结论已部分应用于本科生动量方程实验教学环节，为学生理解实验误差的产生原因提供帮助。