弹性地基上受压矩形纳米板的自由振动与屈曲特性
滕兆春, 刘 露, 衡亚洲
(1. 兰州理工大学 理学院,兰州 730050;2. 江苏兴达钢帘线股份有限公司, 江苏 兴化 225721)
随着纳米技术的发展,纳米器件因具有微小尺寸、超高频率、超低能耗以及优异的力学、化学、电子性能等重要特性,从而使微/纳米机电系统(Micro-Electro-Mechanical System/Nano-Electro-Mechanical System, MEMS/ NEMS)成为电子产品中的核心组件,分析微/纳米机电系统的力学行为是进行安全设计的前提。已有的实验结果表明,基于经典连续介质力学的弹性理论不能准确地预测微/纳米结构的力学行为,这是因为经典连续介质力学没有考虑微/纳米结构中的尺度效应。由Eringen[1]提出的非局部弹性理论弥补了这一缺陷,从而在研究物理和工程领域微/纳米尺度结构的各种问题中得到广泛应用。在已有基于Eringen非局部弹性理论的微/纳米结构研究工作中,Reddy[2]分别采用不同的梁理论(Euler-Bernoulli、Timoshenko、Reddy和Levinson梁理论)研究了非局部效应对梁的弯曲、屈曲和自由振动的影响。Murmu等[3]采用Timoshenko梁理论并运用微分求积法(Differential Quadrature Method, DQM)分析了嵌入弹性介质中的单壁碳纳米管的屈曲问题。刘灿昌等[4]研究了非局部效应对两端固定纳米梁的固有频率以及主谐波共振响应的影响。Nejad等[5]研究了双向功能梯度Euler-Bernoulli纳米梁的弯曲问题。Jandaghian等[6]给出了压电纳米梁自由振动的解析解。Norouzzadeh等[7]基于积分模型的非局部弹性理论用有限元法研究了纳米尺度Timoshenko梁的静态弯曲。张大鹏等[8]基于非局部黏弹性理论,针对非局部阻尼Euler梁在非局部黏弹性地基上的振动特性问题进行了研究。Moosavi等[9]采用剪切变形环理论研究了纳米环的振动问题。Behfar等[10]研究了纳米尺度下多层石墨烯嵌入弹性介质中的振动行为。Pradhan等[11]分别采用经典板理论(Classical Plate Theory, CLPT)和一阶剪切变形理论(First-Order Shear Deformation Theory, FSDT)分析了Winkler地基上四边简支纳米矩形板的固有频率特性,并给出了诸如石墨烯片纳米板自由振动的解析解。Satish等[12]基于非局部连续介质力学并采用两变量精细板理论研究了正交各向异性纳米板的热振动。Kumar等[13]应用非局部连续介质理论分析了嵌入在弹性介质中的石墨烯片的热振动。陈玲等[14]研究了单层石墨烯纳米板的横向自由振动响应,应用纳维解法得到四边简支纳米板振动固有频率的数值解,讨论了小尺寸效应、纳米板的三维尺寸和半波数对振动频率的影响。最近,Ansari等[15]分析了一阶剪切变形磁-电-热弹性纳米板尺寸依赖的屈曲和过屈曲问题,Despotovic[16]研究了体力作用下纳米板的稳定性和振动问题。
纳米板作为最基础的结构元件在MEMS/NEMS中具有重要功能,如用作谐振传感器、生物传感器、原子力显微镜等。同时由于功能和结构的需要,正交各向异性矩形纳米板也常见于MEMS/ NEMS中,深入分析其在面内荷载等多种载荷作用下的力学响应具有理论研究意义和工程实际应用价值。目前,Winkler-Pasternak弹性地基上面内受压正交各向异性矩形纳米板自由振动和屈曲的分析在国内外还鲜见有文献报道,因此本文研究Winkler-Pasternak弹性地基上面内受压正交各向异性矩形纳米板自由振动和屈曲问题。首先基于Eringen非局部弹性理论和经典薄板理论,利用Hamilton原理推导Winkler-Pasternak弹性地基上面内受压正交各向异性纳米板自由振动和屈曲的控制微分方程并进行无量纲化;其次采用微分变换法(Differential Transform Method, DTM)将问题的无量纲控制微分方程及其边界条件进行变换;再将问题退化后与已有文献进行比较后结果一致;最后求解并探讨了无量纲弹性地基系数、载荷参数、和纳米尺度对临界屈曲载荷的影响以及无量纲弹性地基系数、无量纲压力强度、载荷参数、长宽和纳米尺度对于矩形纳米板自振频率的影响。
1 控制微分方程及参数的无量纲化
考虑如图1所示的正交各向异性矩形板,将其放置在均匀Winkle-Pasternak弹性地基上并建立图示的笛卡尔直角坐标系。假定正交各向异性方向与x轴和y轴方向一致。板的尺寸为a×b×h且受到垂直于y轴截面上的面内分布力Ny=-N0(1-γx/a),其中N0为x=0处的压力强度,γ为载荷参数。这里用λ=a/b表示矩形板的长宽比,用kw,kp分别表示Winkler-Pasternak弹性地基的弹性刚度系数和剪切刚度系数,垂直于板面的位移分量为w。y=0和y=b处为简支边界(S),其余对边为简支(S)或夹紧(C)边界。下面在对纳米矩形板四个直边的边界条件表示中,均按x=0,y=b,x=a和y=0处的次序给出。
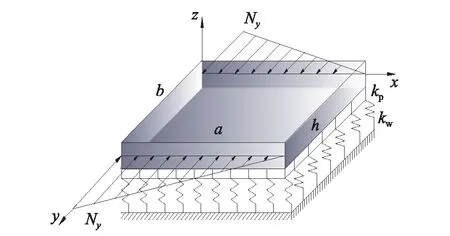
图1 Winkler-Pasternak弹性地基上面内受压正交各向异性矩形纳米板Fig.1 In-plane compressed orthotropic rectangular nanoplate resting on a Winkler-Pasternak foundation
为了导出正交各向异性矩形纳米板自由振动控制微分方程,运用Hamiltion原理表示为
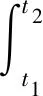
(1)
式中:t为时间;δ为变分符号;U,T和W分别为正交各向异性矩形板的应变能、动能和外力势能,各量可表示为
(2)
(3)
(4)
式中:σx,σy和τxy为三个应力分量;εx,εy和γxy为三个应变分量;ρ为质量密度。
正交各向异性矩形板中面应变和内力分量为[17]
(5)
(6)
将式(2)~式(6)代入式(1)可得Winkler-Pasternak弹性地基上面内受压正交各向异性矩形板的运动方程为
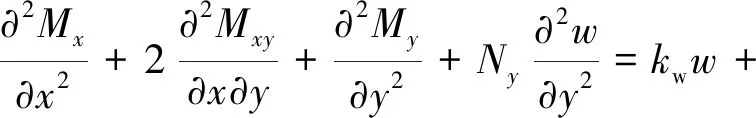
(7)

由Eringen非局部弹性理论,在一点x处的应力不仅取决于该点的应变,也取决于连续体中该点附近点的应变。因此,对于均匀的线弹性体V在x点的非局部应力张量σij可表示为
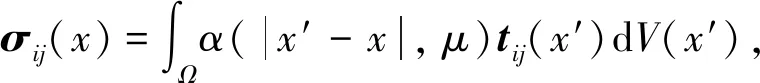
(8)
式中:σij(x)为x点的应力张量;tij(x′)为任意点x′与线性应变张量εkl(x′)对应的宏观(经典)应力张量;Cijkl为四阶弹性张量;α(|x′-x|,μ)为非局部模量的核函数;|x′-x|为欧氏距离;μ=e0a0/l为依赖于内部和外部特征长度的无量纲参数,称为纳米尺度,其中e0为一个非局部的材料常数,a0为内部特征长度;l为外部特征长度。
二维情形下的非局部应力可近似表示为一个二阶微分方程[18]

(9)
在二维形式的纳米板应力应变关系为
(10a)
(10b)

(10c)
式中:E1,E2,G12分别为正交各向异性材料的三个弹性模量;v12,v21为泊松比。
由式(5)、式(6)和式(10)可得正交各向异性矩形纳米板的弯矩和扭矩方程为
(11a)
(11b)
(11c)
式中:D11=E1h3/[12(1-v12v21)],D66=G12h3/12,D22=E2h3/[12(1-v12v21)],D12=v21D11=v12D22,为四个弯曲刚度。
式(11a)~式(11c)代入式(7)可得Winkler-Pasternak弹性地基上面内受压正交各向异性矩形纳米板的非局部运动方程为

(12)
正交各向异性矩形纳米板的边界条件在y=0和y=b处若只考虑为简支(S),板的横向位移函数可取为
(13)
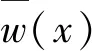
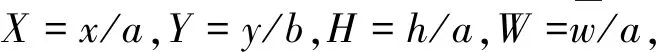
Ω2=[12ρ(1-v12v21)a2ω2]/E1H2,
N0*=[12N0(1-v12v21)]/aE1H3,
Kw=(1-v12v21)akw/E1,
Kp=(1-v12v21)kp/aE1
并由式(12)~式(13)可得Winkler-Pasternak弹性地基上面内受压正交各向异性矩形纳米板自由振动的控制微分方程为
(14)
其中,
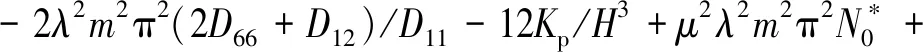
μ2Ω2-12μ2Kw/H3-24μ2λ2m2π2Kp/H3,
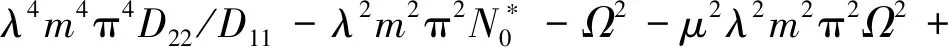
12μ2λ2m2π2Kw/H3+12λ2m2π2Kp/H3+
又由弹性稳定性理论可知,结构失稳时的振动具有无限大的振动周期,其固有频率为零[19],则式(14)中若取Ω=0,则可得到计算Winkler-Pasternak弹性地基上面内受压正交各向异性矩形纳米板各阶屈曲模态载荷的控制微分方程,其最小值即屈曲临界载荷。至于在X=0和X=1边界处,可为简支(S)边界条件或者夹紧(C)边界条件,其无量纲形式表述为
简支(S)
(15)
夹紧(C)
(16)
2 无量纲控制微分方程及其边界条件的DTM变换
弹性地基上面内受压正交各向异性矩形纳米板自由振动和屈曲的无量纲控制微分方程式(14)为变系数常微分方程,一般情况下较难求得其解析解,这里采用微分变换法(DTM)[20-23]进行求解。DTM是一种能有效将线性或非线性微分方程(组)变换成代数方程(组)求解的半解析方法,它基于Taylor级数展开来求解微分方程,使用充分可微的多项式形式作为精确解的近似。经DTM变换,可将原微分方程(组)和系统边界条件转化为由离散函数构成的代数方程(组),非常适合计算机编程进行求解。对于原函数f(x),根据函数的Taylor公式,经过DTM变换后的函数F[k]定义为
(17)
F[k]的逆变换为
(18)
或者
(19)
在实际应用中,函数f(x)只考虑级数的有限项,式(14)可重写为
(20)
式中:正整数r为Taylor级数的项数。通常情况下r的取值则取决于求解方程的收敛状况和需要的精度。
运用DTM对Winkler-Pasternak弹性地基上面内受压正交各向异性矩形纳米板自由振动和屈曲问题进行求解时,首先需要将其无量纲控制微分方程和边界条件经DTM转化为相应的由离散函数组成的代数方程。这里用F表示式(14)中W经DTM变换后的离散值,则式(14)由DTM可变换为
B1F[k+4]+B2F[k+2]+B3F[k+1]+
B4F[k]+B5F[k-1]=0
(21)
其中,
B2=[-2λ2m2π2(2D66+D12)/D11+μ2Ω2-12μ2Kw/H3+
24μ2λ2m2π2Kp/H3](k+1)(k+2),
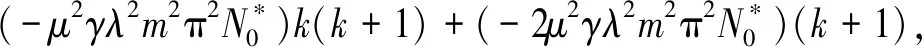

12μ2λ2m2π2Kw/H3,
边界条件变换为
在X=0处,简支(S)边界条件
F[0]=F[2]=0
(22)
夹紧(C)边界条件
F[0]=F[1]=0
(23)
在X=1处,简支(S)边界条件
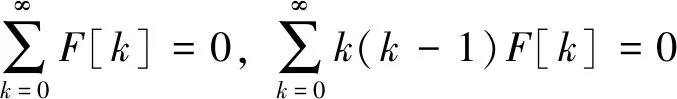
(24)
夹紧(C)边界条件
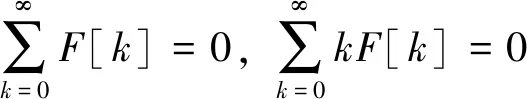
(25)
将式(21)分别代入式(22)和式(24),式(22)和式(25),可分别求得四边简支(SSSS)和三边简支一边夹紧(SSCS)的频率特征方程为
(26)
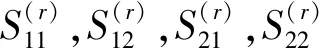
(27)
要使式(27)有非零解,则
(28)
令无量纲固有频率Ω=0,给定参数可以求解出临界屈曲载荷Ncr。Ncr的求解过程类似于Ω的求解过程,同理可得
(29)
在对边简支对边夹紧(CSCS)、一边夹紧三边简支(CSSS)的边界条件下,同理可求出含有未知量无量纲固有频率Ω以及临界屈曲载荷Ncr特征方程
(30)
(31)
由式(28)~式(31),SSSS,SSCS,CSCS,CSSS边界条件下的无量纲固有频率Ω和临界屈曲载荷Ncr可求出。为了控制求出的无量纲固有频率Ω和临界屈曲载荷Ncr的精度和研究其收敛性,则有
(32)
式中:η1,η2为迭代误差限,这里取η1=η2=0.000 001。
3 计算结果与分析
通过编写MATLAB程序可获得由DTM求解Winkler-Pasternak弹性地基上面内受压正交各向异性矩形纳米板屈曲和振动特征值问题的临界载荷Ncr和无量纲频率Ω。为了验证求解方法的正确性和精度,通过式(14)将原问题分别退化为各向同性矩形纳米板和Winkler-Pasternak弹性地基上面内受压各向同性矩形板。表1为λ=1,v=0.3,a=10 mm时SSSS边界条件下各向同性矩形纳米板的无量纲固有频率Ωnm与文献[24]的样条有限条法(Spline Finite Strip Method, SFSM)的计算比较,结果一致。其中下标n=1,2,3,…,和m=1,2,3,…,分别表示板在x方向和y方向上振动的半波数。表2为m=1,v=0.3时CSCS边界条件下各向同性矩形板临界屈曲载荷Ncr与文献[25]的计算比较,结果也一致。
在研究Winkler-Pasternak弹性地基上面内受压正交各向异性矩形纳米板自由振动和屈曲特性中,选择一石墨环氧树脂材料的正交各向异性矩形纳米板进行计算。其材料参数[26]如下:vLT=0.23,EL=60.7 GPa,ET=24.8 GPa,GLT=12.0 GPa。式中:L,T分别为正交各向异性材料的纵向和横向且表示意义与笛卡尔坐标轴一致。例如L/T方向表示各向异性材料的纵向与x轴一致,横向与y轴一致;T/L方向表示各向异性材料的横向与x轴一致,纵向与y轴一致。计算中以L/T方向为例:v12=0.23,D22/D11=0.408 567,D12/D11=0.093 970,D66/D11=0.193 421。
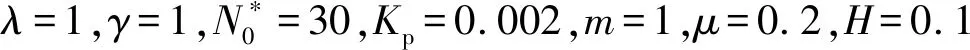
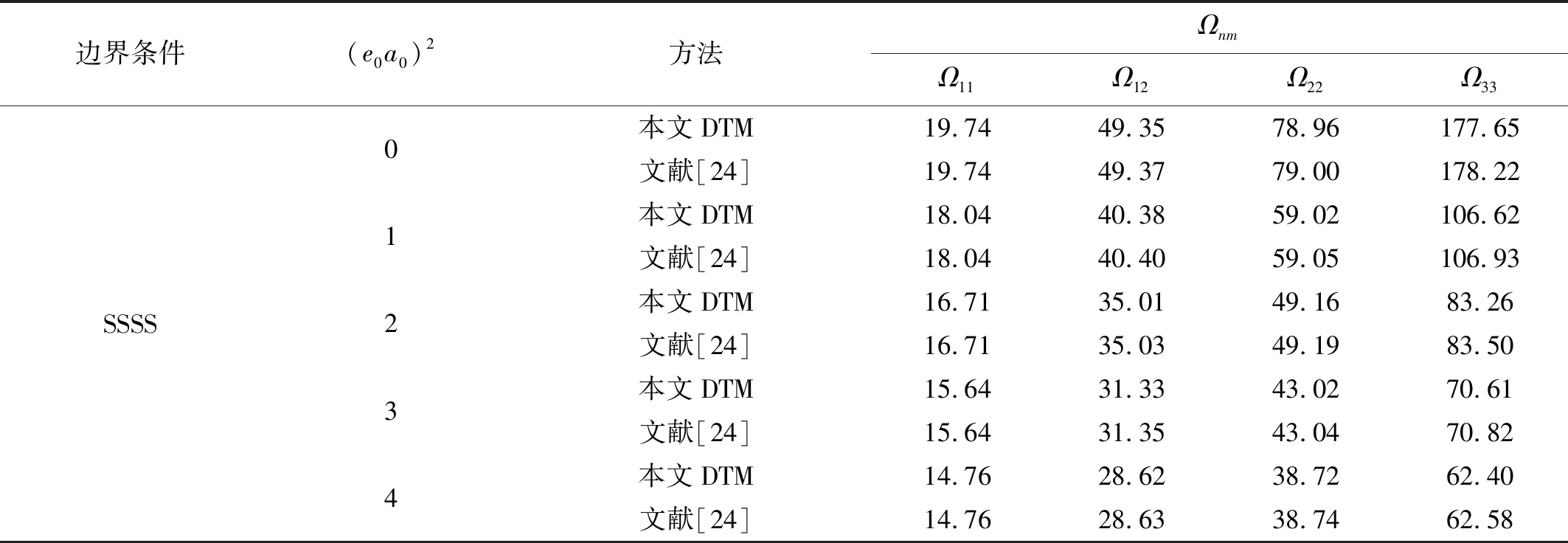
表1 各向同性矩形纳米板的无量纲固有频率Ωnm
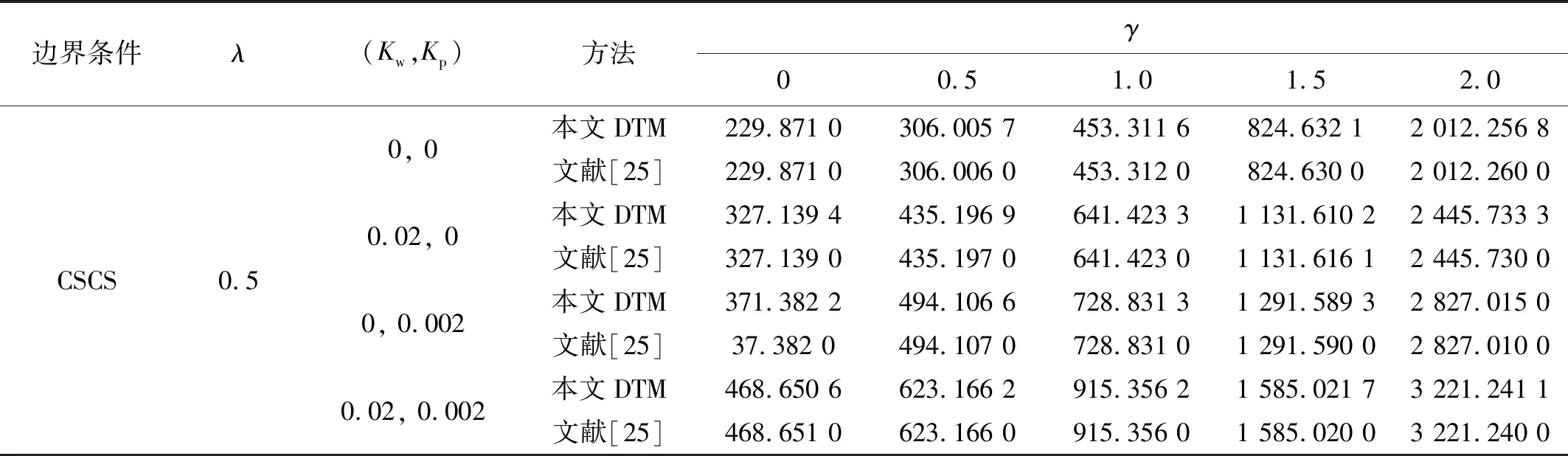
表2 各向同性矩形板临界屈曲载荷Ncr
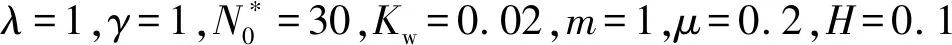
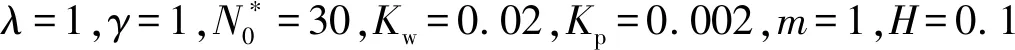
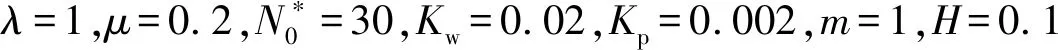
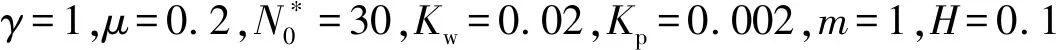
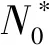
图2 不同边界条件下前三阶无量纲固有频率Ω与Winkler地基刚度系数Kw的关系曲线Fig.2 First three dimensionless natural frequencies Ω vs the stiffness coefficient Kw of Winkler foundation for different boundary conditions
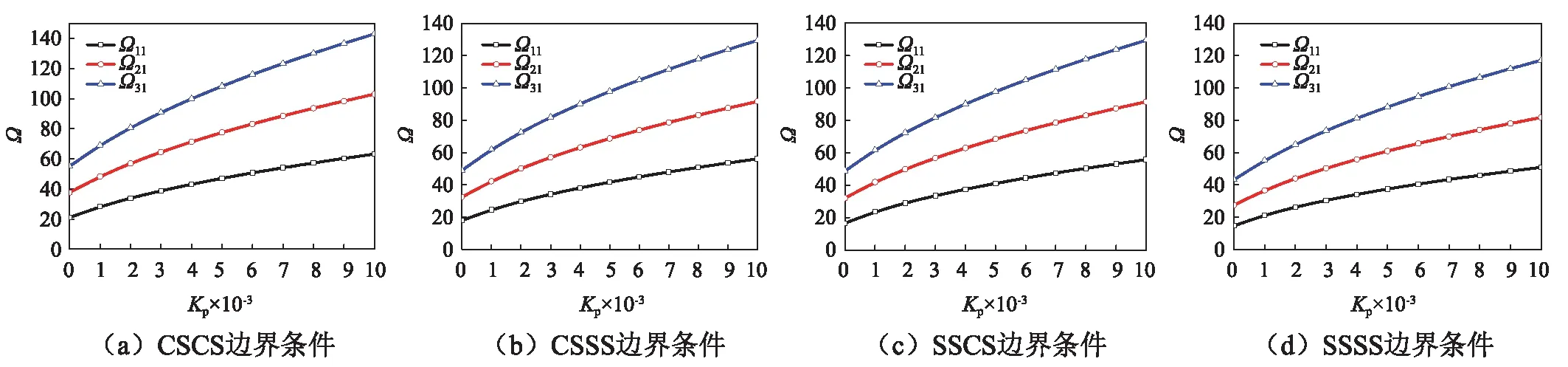
图3 不同边界条件下前三阶无量纲固有频率Ω与Pasternak地基刚度系数Kp的关系曲线Fig.3 First three dimensionless natural frequencies Ω vs the stiffness coefficient Kp of Pasternak foundation for different boundary conditions
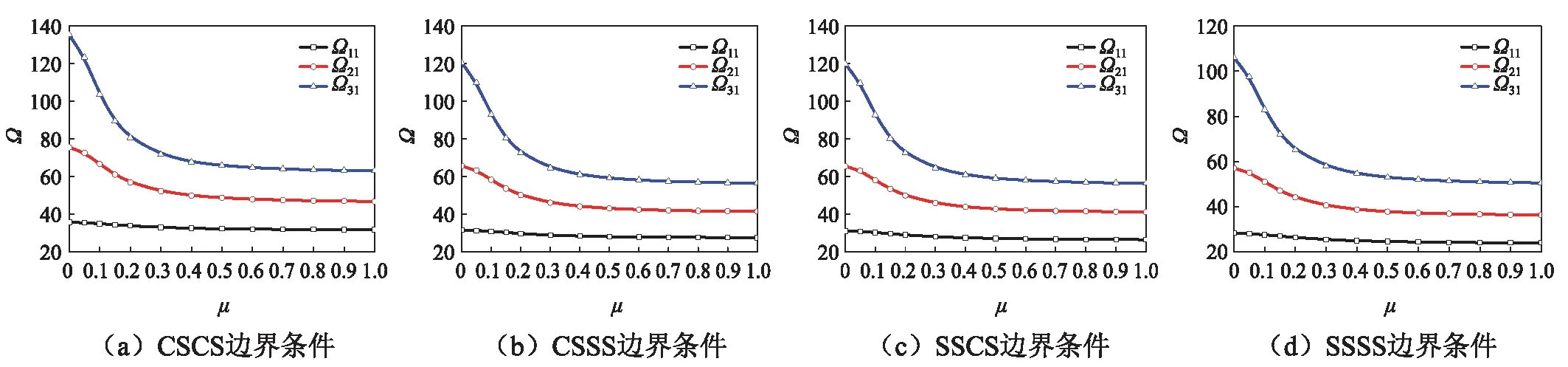
图4 不同边界条件下一阶无量纲固有频率Ω与纳米尺度μ的关系曲线Fig.4 First dimensionless natural frequencies Ω vs the nanoscale factor μ for different boundary conditions
图5 不同边界条件下一阶无量纲固有频率Ω与载荷参数γ的关系曲线Fig.5 First dimensionless natural frequencies Ω vs the load parameter γ for different boundary conditions
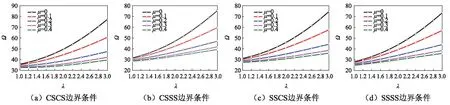
图6 不同边界条件下一阶无量纲固有频率Ω与长宽比λ的关系曲线Fig.6 First dimensionless natural frequencies Ω vs the aspect ratio λ for different boundary conditions
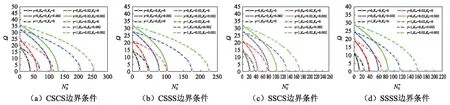
图7 不同边界条件下一阶无量纲固有频率Ω与X=0处无量纲压力强度的关系曲线Fig.7 First dimensionless natural frequencies Ω vs dimen-sionless pressure intensity at X=0 for different boundary conditions
表3为λ=1,γ=1,m=1,μ=0.2,H=0.1,Ω=0时CSCS和CSSS边界条件下正交各向异性矩形纳米板的临界屈曲载荷Ncr。由表3可知,临界屈曲载荷Ncr的数值大小随弹性地基系数的增大而增大。
表4为λ=1,m=1,H=0.1,Kw=0.02,Kp=0.002,Ω=0时在CSCS和CSSS边界条件下正交各向异性矩形纳米板的临界屈曲载荷Ncr。表4中特别当γ=1.5,γ=2.0时,正交各向异性矩形纳米板同时受拉和受压,这样存在两个临界屈曲载荷(一正一负)。由表4可见:当Kw,Kp,λ一定时,正的临界屈曲载荷Ncr数值大小随γ的增大而增大,但负的临界屈曲载荷Ncr数值大小随γ的增大而迅速减小;临界屈曲载荷Ncr数值大小随纳米尺度μ的增大而减小。
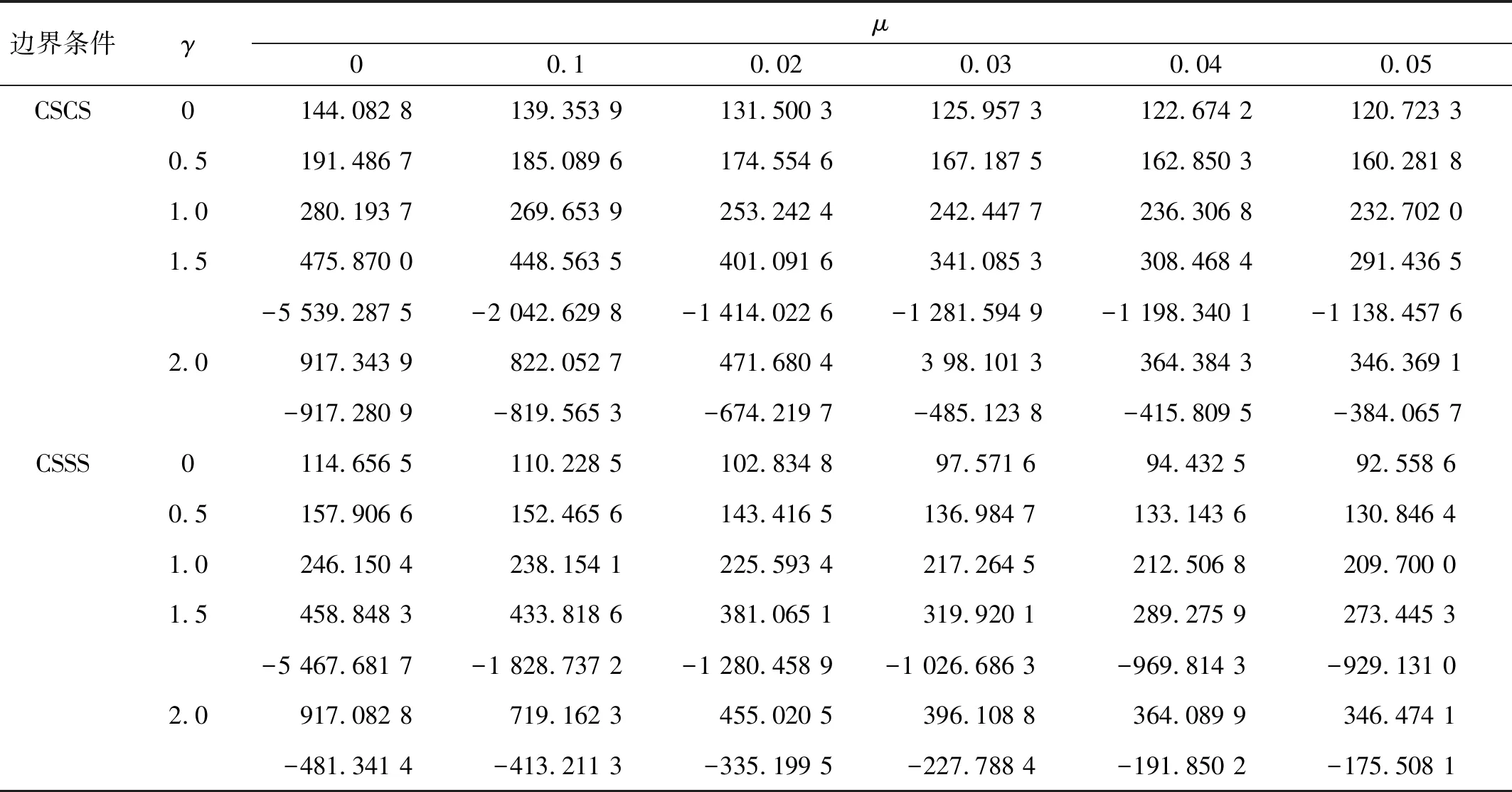
表4 不同边界条件下Winkler-Pasternak弹性地基上面内受压正交各向异性矩形纳米板的屈曲临界载荷Ncr
4 结 论
本文基于Eringen非局部弹性理论和经典薄板理论,利用Hamilton原理推导了Winkler-Pasternak弹性地基上面内受压正交各向异性矩形纳米板自由振动和屈曲问题的控制微分方程并进行无量纲化,采用DTM求解并研究了纳米板的自由振动与屈曲特性。将问题退化后与已有文献进行比较后发现结果一致。考虑各参数对不同边界条件下纳米矩形板的自振频率Ω和临界屈曲载荷Ncr的影响。矩形纳米板边界条件考虑对边简支,其余两边可为简支或夹紧任意组合,因此本文的分析过程能处理矩形纳米板相对较多的边界条件。主要结论如下:
(1)随着弹性地基模量Kw和Kp的增大导致板系统的刚度增大,从而使得各边界条件下正交各向异性矩形纳米板自振频率Ω增大以及临界屈曲载荷Ncr增大。
(2)随着纳米尺度μ的增大,正交各向异性矩形纳米板的自振频率Ω和临界屈曲载荷Ncr都减小,这是由于非局部效应使得纳米结构的刚度减小,从而降低了板的自振频率和临界屈曲载荷。
(3)随着载荷参数γ的增大导致了板系统受到垂直于y轴截面上的面内分布力Ny减小,从而使得正交各向异性矩形纳米板的自振频率Ω和正的临界屈曲载荷Ncr都增大;但负的临界屈曲载荷Ncr数值大小随γ的增大而迅速减小。
(5)较强约束的边界条件下自振频率Ω和临界屈曲载荷Ncr值较大,且在计算低阶频率值和约束较弱边界条件下频率值时收敛较快。

