一种山区峡谷桥址区风场特性数值模拟方法
靖洪淼, 廖海黎,2, 周 强,2, 马存明,2
(1.西南交通大学 土木工程学院,成都 610031;2.风工程四川省重点实验室,成都 610031)
近年来,山区建造大跨度桥梁、大跨空间结构等风敏感性基础设施的情况逐渐增多。对于此类柔性结构而言,建设场地的强风特性是决定其风致响应的关键因素之一,有时甚至是控制其结构设计的决定性因素。现有的相关抗风设计规范[1]也大多针对平原、缓丘和沿海地区,不能直接用于确定复杂山区峡谷地形桥址处的风场特性。对此,目前主要有三种方法用于研究并确定复杂地形的风场特性,分别是:现场实测、地形模型风洞试验和CFD(Computational Fluid Dynamics)地形数值模拟。
现场实测方法是直接最有效获取风场特性参数的手段,尤其是脉动风速特性中的风速谱、紊流强度、紊流积分尺度、阵风系数等。例如张明金[2-4]等,在现场建立测风塔,安装风场实时监测系统,得到了较为完备的山区峡谷地形桥位处的风场特性。但是,该方法需要很长的数据采集时间,现场条件苛刻,耗费大量的人力、物力和财力。地形模型风洞试验很好的避免了现场实测方法的缺点,如试验周期短,试验条件容易控制,模型制作简便,试验数据可靠等。Xu等[5-9]采用地形模型风洞试验方法,研究了复杂山区峡谷地形桥址处的风场空间分布特性。受风洞试验条件的限制,地形模型表达的地理范围和采用的比例尺一般都很小。此外,地形模型风洞试验无法保证雷诺数一致性要求,其试验结果准确性还有待进一步研究。CFD地形数值模拟很好地解决了现场实测和地形风洞试验中的缺点,如地形范围可任意选取,风速和风向可任意设置,费用最少,周期短等。目前采用CFD方法研究风场特性也是一大热点,例如李永乐等[12-13]采用了地形CFD数值模拟方法,得到了较大范围复杂地形的风场特性。Ren等[14]利用数值模拟方法,研究了河南某地的风场特性,并在此基础上提出了一种新的复杂地形空间风场预测模型。Jubayer等[15]同样采用数值模拟方法,研究了一个较大区域地形风场特性,并以数值模拟结果为基础设置地形风洞试验入口条件,最终得到了更加接近实际情况的风场特性。此外,部分文章还对地形过渡段形式做了研究并应用,例如胡朋等[16]基于理想流体圆柱绕流推导出一类过渡段曲线, Ren等采用了一种平方余弦函数用于计算域边界平滑过渡。
虽然CFD地形数值模拟得到了普遍的研究和应用,但入口风速条件设置、地形计算区域选取、地形边界过渡形式等方面还不明确,如入口的参考风速仍然很随意,使得数值模拟雷诺数和实际雷诺数严重不相符;截取矩形地形作为计算区域,难于保证风场的充分发展,这些都会导致计算结果的合理性和准确性不足。为此,本文提出了一种新型的山区峡谷桥址处风场特性数值模拟研究方法,合理地设置了计算域,确保风场充分发展;并采用“虚拟标准气象站”法获取较合理的入口边界条件,使数值模拟雷诺数与实际雷诺数尽量一致。最终,根据本文提出的数值模拟方法,得到了较为准确的山区峡谷桥位处风场特性参数,也为该类地形数值模拟研究提供了一定参考。
1 数值计算模型
某待建大跨度桥梁走向以及桥位附近的地形如图1所示,从图中可以看出,河道总体呈西南到东北走向,在桥位处几乎与待建桥梁垂直。桥位四周均有海拔达1 000 m以上的山峰,并且数量众多。桥位附近东部和北部相对平坦,海拔较低,而远处却是海拔较高山峰。因此该地区地形十分复杂,其风环境也非常复杂。
1.1 地形和计算域
本文采用imageware软件,直接利用散点云图数据生成地形曲面,即首先基于SRTM(Shuttle Radar Topography Mission)数据(SRTM数据是根据美国太空总署、国防部国家测绘局以及德国与意大利航天机构共同合作完成联合测量的雷达影像数据,绘制成的数字地形高程模型),在专业地形软件Global Mapper中,提取三维地形散点云图,然后,导入imageware软件,直接利用上述散点云图构建三角形网格地形曲面。最后在地形曲面上选取以桥位为中心的半径5 km的圆形地形范围。其中三维地形散点云图的水平解析度是30 m,以及圆形地形范围内最高和最低海拔相差约750 m,imageware软件拟合的地形曲面与原数字高程数据的误差不超过5%。

图1 桥位处地形图Fig.1 Terrain at bridge site
由于桥位处地形非常复杂,而且地形解析度有限,所以导致计算域边界十分陡峭。为减少地形边界突变对风场模拟结果的影响,确保获得更符合实际的风场选取的地形边界需要做延伸以及光滑处理。本文利用ICEM软件中的B-Spline曲面形式作为过渡面,连接地形边界与计算域底面,如图2所示。此外由于选取的地形区域面积足够大,当气流发展到桥位处时,边界过渡段的影响基本可以忽略。在本研究中,地形计算域的过渡段的距离为1 km,而Liu 等[17]在30 km×30 km的计算域中仅采用了1 km长度的过渡段,并取得了较好的模拟结果。显然本文计算域远远小于Liu等采用的计算域,但仍然采用1 km的过渡段,因此上述处理方式可以满足数值模拟的需要。最终处理后的地形如图3所示,其中待建桥梁主梁和地形边缘的海拔高度差为70 m。
为了确保风场的充分发展,并兼顾工况设置,总体计算域在圆形地形区域上,采用长方体形式,长宽高分别为:30 km,20 km和3 km,如图4所示。计算域的阻塞率不超过5%。所关注的地形区域(半径为6 km的圆形区域)位于总长方体计算域中心,而且可以绕圆心旋转,便于改变来流方向,从而满足设置不同计算工况的要求。

图2 地形边界过渡形式Fig.2 Transition of terrain edge
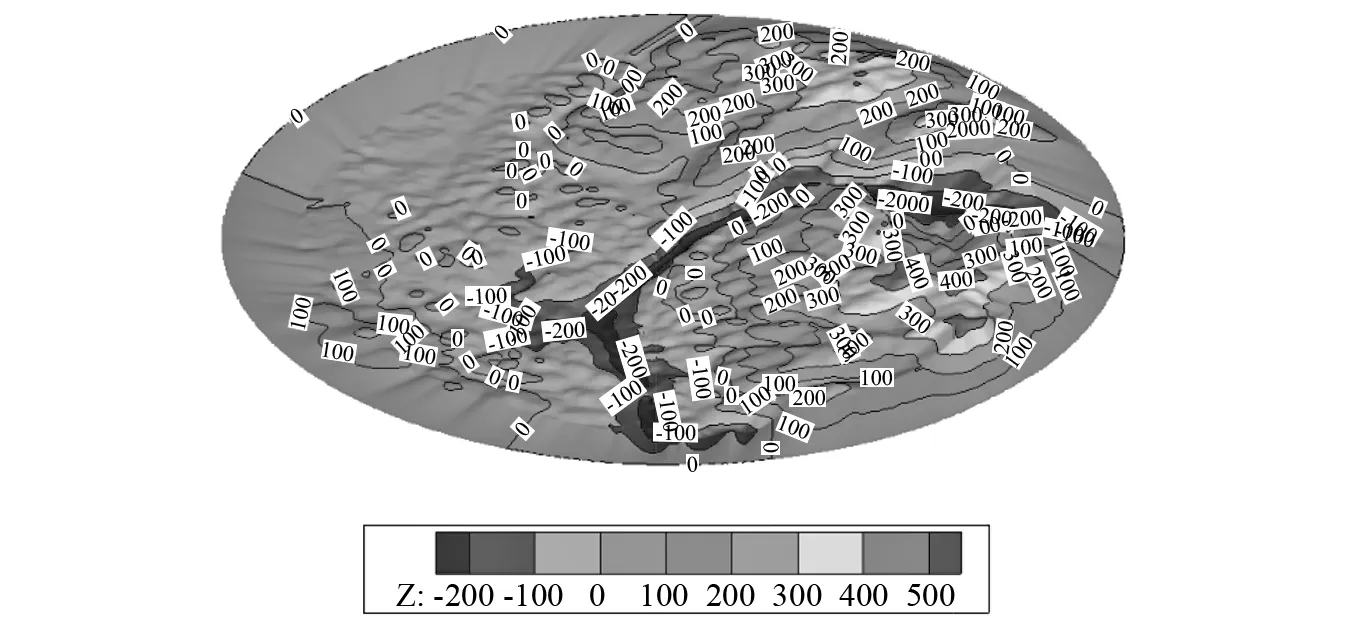
图3 地形三维曲图Fig.3 Three-dimensional terrain
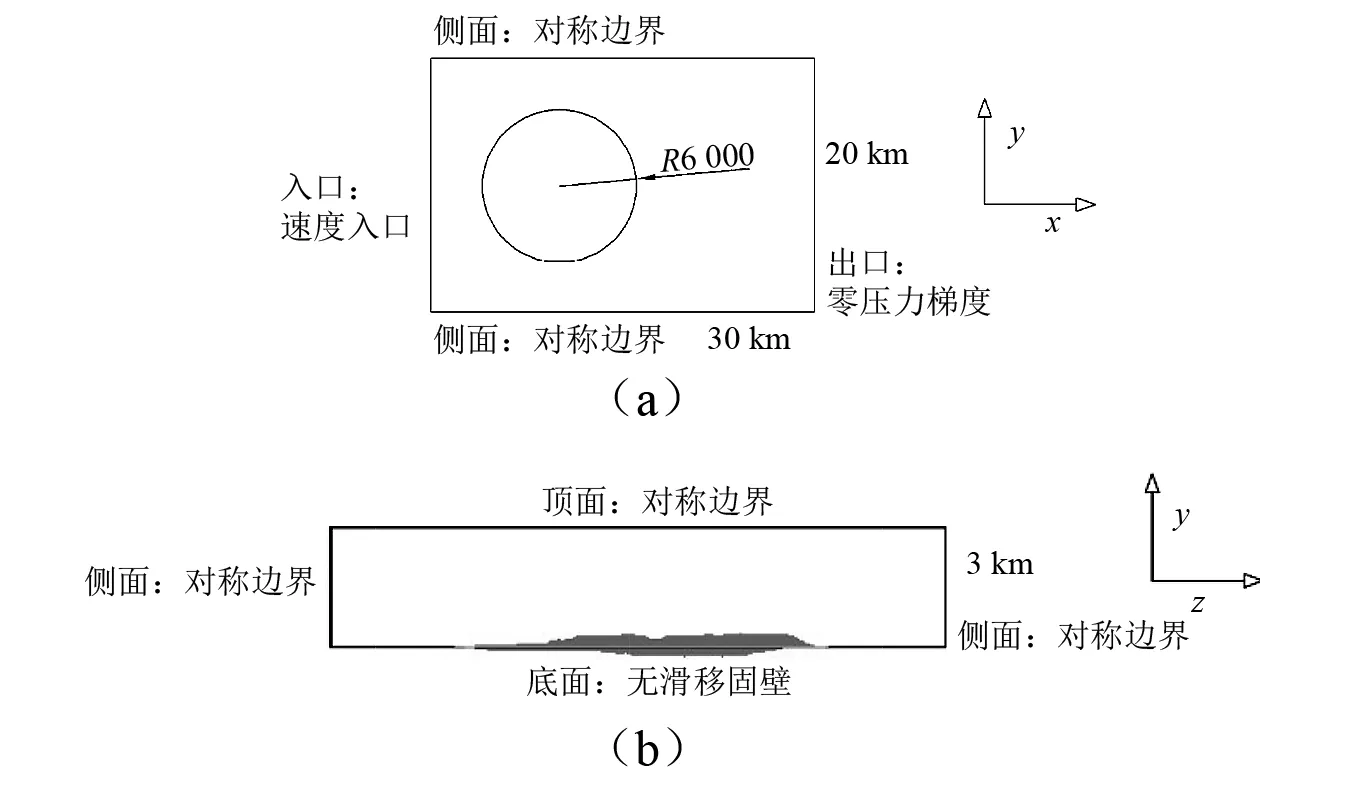
图4 计算域Fig.4 Computational domain
1.2 网格划分
如图5所示,整个计算域分成两个部分:外部区域和内部圆柱地形区域。其中外部区域比较规则,因此采用正交性较好的六面体结构化网格划分;内部地形很复杂,因此采用适应性更好的四面体非结构化网格划分。内部地形表面采用了10层边界层网格,其中第一层网格的水平间距不超过40 m。针对第一层网格竖向高度,根据相关文献给出的经验值(如李永乐等、Ren等、Liu等和祝志文等[18]给出的第一层网格高度分别为10 m,5 m,6 m和5 m),本文设定为5 m,故其y+值为500左右。Blocken[19]指出y+≈500以内属于边界层,且在边界层内可采用壁面函数处理,节省计算资源而且获得较精确的计算结果。因此,本文在地形表面增设了壁面函数(nut-K wall function),以确保数值计算的精度。此外,Liu等指出地表树木等植被的平均高度为15 m,第一层网格高度小于此值即可满足要求,即本文设置的第一层网格高度满足此要求。由于地形复杂,在内部圆柱地形区域采用非结构化的四面体网格,因此,地表附近部分网格质量稍差,但质量也在0.35以上,其余部分网格质量均大于0.5。外部区域采用结构化六面体网格划分,底层网格高度为5 m,从下往上也是按照1.2的比例逐渐增大。总体网格数量约为420万。
1.3 湍流模型和边界条件
在风场数值模拟中,选取了对流动分离具有较好解析度的k-ωSST湍流模型。采用有限体积法对计算域流场进行离散,由于复杂地形下桥梁抗风安全性更关心平均风特性,而且计算流场充分发展后的平均风场特性接近稳态计算结果,因此本文采用了稳态不可压缩simpleFoam求解器。压力与速度耦合采用simple算法。对流项和黏度项采用了二阶中心差分格式离散。
如图4所示,上面、下面和顶面为对称边界条件(symmetry),地面采用无滑移固定壁面(No-Slip)。由于本计算采用的计算域较大,在出口边界上流场已得到充分发展,故出口边界采用开放式零压力出口(Open pressure)。由于桥梁主梁距地表的高度远远大于地表植被等的高度,因此在数值模拟中并未考虑地表粗糙度。内部和外部网格交界面采用cyclicAMI边界条件,该种边界条件允许速度和压力的传递。计算域入口为速度入口(Velocity inlet)边界条件,按大气边界层C类指数风剖面(粗糙度系数为0.22)形式从计算域入口底面开始设置;在梯度风高度450 m以上,风速采用固定值。
为了更加科学地设置入口桥位高度处的参考风速,使模拟地形风场的雷诺数更加符合实际情况,采用了“虚拟标准气象站”法[20]计算入口桥位高度处的风速值。现假定在桥位主梁高度处设立虚拟气象站,该站的平均海拔高度取为688 m。从《公路桥梁抗风设计规范》中,可以查出桥位200 km范围内8个地区的海拔和对应的百年风速,见表1。图6给出了表1中各气象站点最大风速随高度变化的情况,并利用最小二乘法对数据进行拟合,得到桥位处虚拟气象站重现期为100年的风速随海拔高度变化的曲线。利用拟合的风速-海拔高度公式,可得该虚拟气象站的百年一遇的最大风速为24.75 m/s。将24.75 m/s作为桥位虚拟气象站的基本风速U10。入口采用指数风速形式,根据桥位周围的地形情况,取为C类地形,即地面粗糙度系数α=0.22,湍流度取5%。入口指数风速表达式为式(1),如前面所述,桥梁主梁到计算域入口底边的相对高度是70 m,所以入口桥位高度处的风速为37.97 m/s。
(1)
式中:z为距计算域入口底边的距离,m;Uz为距计算域入口底边距离z处的风速,m/s。

图5 计算域网格信息Fig.5 Mesh system
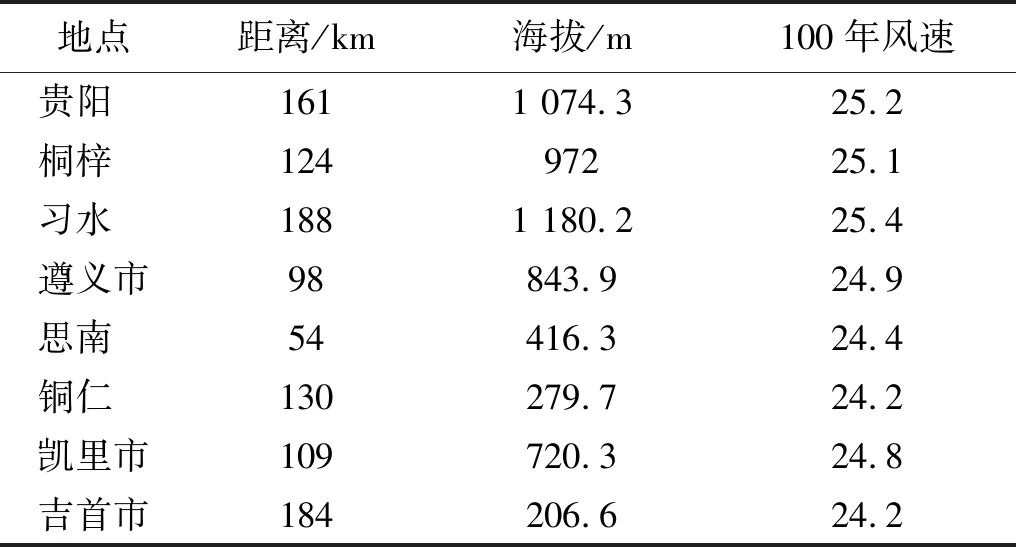
地点距离/km海拔/m100年风速贵阳1611 074.325.2桐梓12497225.1习水1881 180.225.4遵义市98843.924.9思南54416.324.4铜仁130279.724.2凯里市109720.324.8吉首市184206.624.2
1.4 工况说明
在实际情况中,影响桥梁工程安全的主要是横桥向来流,同时为了说明本文数值模拟的合理性,这里设置了6种不同来流风向,见图7所示,并以此设置工况编号(图中圆圈内数字)。工况1、工况2和工况3的水平夹角依次为15°;工况4、工况5和工况6的水平夹角也依次为15°。主梁考察点见图8所示,共18个,依次均匀分布在两个桥塔之间的主梁上。两个桥塔间距为680 m,因此主梁相邻观测点间距为40 m。此外,为了得到桥位处风速剖面情况,分别在1/4跨、跨中和3/4跨处从下往上依次设置了30个观测点。其中相邻观测点之间的竖向间距为20 m,最底部观测点到主梁的距离为60 m。
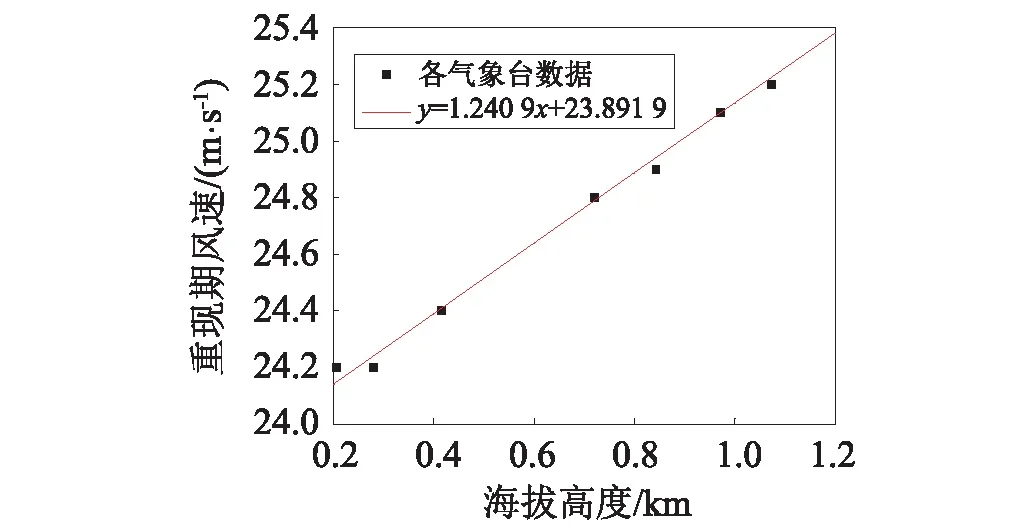
图6 桥位附近气象站点最大风速随高度的变化Fig.6 Variation of maximum wind speed with height of weather stations near the bridge site
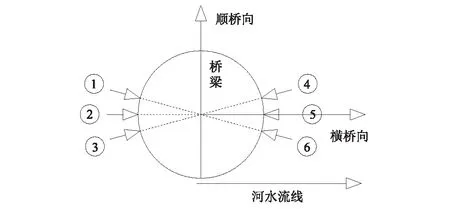
图7 工况示意图Fig.7 Diagram of load cases
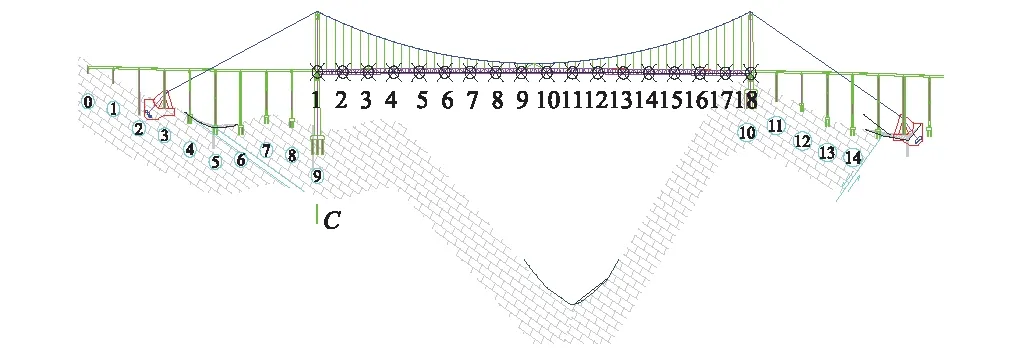
图8 主梁观测点布置示意图Fig.8 Diagram of measurement points at the bridge girder
2 结果与讨论
由于本文采用的是稳态计算,故选取流动充分发展的状态为最终流场状态。如图9所示,中心平面上远离地形的尾流区域的压力梯度约为零,即表明流动已得到充分发展。

图9 中心剖面压力云图Fig.9 Pressure contour of center plane
基于上述最终流场状态,分析了山区峡谷桥址处的风场特性,得到了拟建桥梁主梁上的水平风速、风攻角α、风向角β和风速放大系数Cu等,以及主梁1/4跨、中跨和3/4跨处的平均风速剖面情况,并结合CFD数值模拟流迹显示的优点,研究了桥址处山体等地形对风场特性的影响机理。风攻角α、风向角β和风速放大系数Cu的计算表达式见式(2)~式(4)。
(2)
(3)
(4)
式中:u,v,w分别为主梁上横桥向,顺桥向和竖向风速分量;vb为主梁上的测点风速,v0为入口主梁高度处的风速。
2.1 平均风速沿主梁分布
为了便于桥梁工程抗风设计的需要,主梁水平方向的风速分解为顺桥向和横桥向,并无量纲化,参考风速为主梁高度入口处的风速,如图10和图11所示。从图10的主梁横桥向风速可以看出,工况4和工况6中部分横桥向风速较大,其中工况4为主梁前半段,工况6为主梁后半段,另外工况5的横桥向风速普遍较大。以工况5为例,从图12的主梁流线图中可以看出,由于河道和两岸地势的原因,来流在主梁处发生了汇聚,产生了明显的“峡谷效应”,工况4和工况6的主梁流线图也基本同上。另外,工况2的主梁左半段风速明显相对较小,分析其主梁流线图(见图13)可以发现,由于其上游地形比较复杂,有两股来流汇聚到主梁上,其中主梁左半段由上部来流控制。这股来流在上游发生了翻转,特别是到达主梁前,较高的地势对来流产生了阻挡和分散作用,因此导致风速变小。而下部来流在河道均处于汇聚状态,流经主梁时处于山体迎风坡顶部,产生了加速作用。
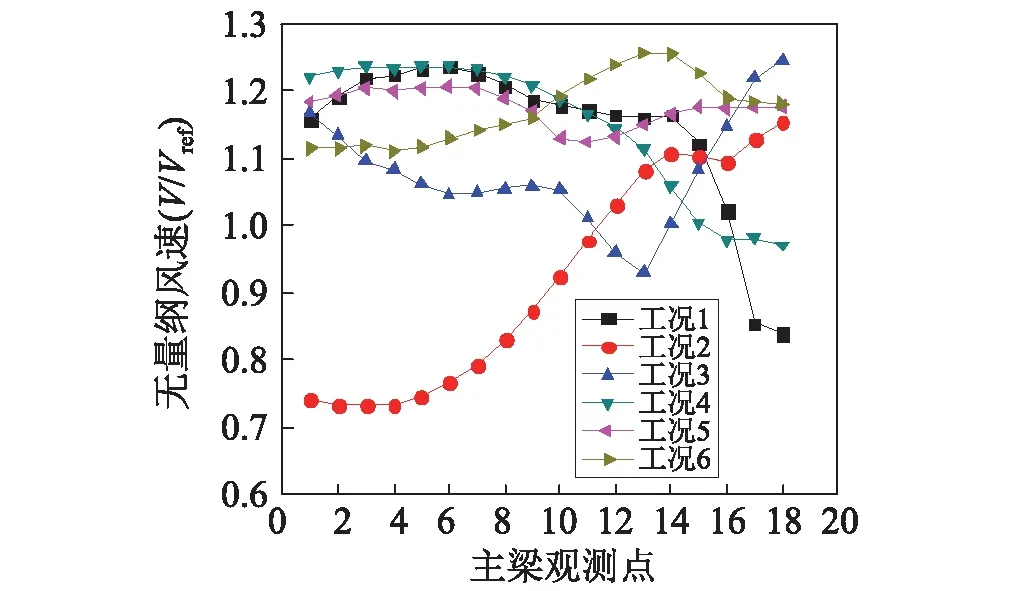
图10 主梁横桥向风速分布Fig.10 Distribution of transverse wind speed along the bridge girder
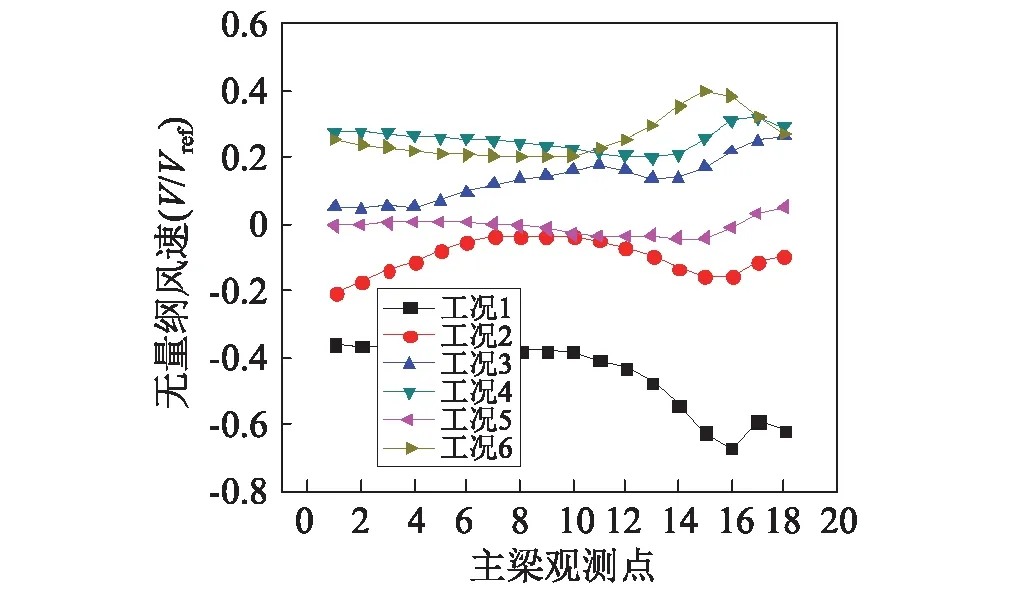
图11 主梁顺桥向风速分布Fig.11 Distribution of longitudinal wind speed along the bridge girder

图12 工况5的主梁流线图(左侧为风速入口)Fig.12 Streamline of case 5 (inlet on the left)
对于顺桥向风速,随着来流和桥梁横桥向夹角的增大,风速也由小变大,并且整体分布比较均匀。由于地形相对平缓,该段河道相对平直,因此上下游来流时,顺桥向风速线型比较一致,大体呈对称分布,如工况1和工况6。

图13 工况2的主梁流线图(左侧为风速入口)Fig.13 Streamline of case 2 (inlet on the left)
2.2 平均风速沿高度分布
为了研究山区峡谷桥址处平均风速沿高度的分布情况,图14、图15和图16分别列出了主梁1/4跨、中跨和3/4跨处,从主梁下60 m到主梁上520 m的风速剖面。从图中可以看出,当河道下游来流时(对应的工况为4、工况5和工况6),上述三个跨度的风剖面都比较符合指数形式。这是因为下游地形相对海拔较低,地势相对平坦,没有突出的山峰或峭壁,河道也比较平直,因此整个地形对来流的阻挡作用很小,最终导致桥位处的平均风速风剖面形式比较符合指数形式。但是,当河道上游来流时(对应的工况为1、工况2和工况3),上述三个跨度的风剖面变化非常大,有些已经完全无法用指数风剖面形式表示。产生这种情况的原因是,河道上游地形十分复杂,并出现了河道转折,在转折处又存在悬崖,河谷、山谷和峭壁交错出现,使来流发生翻转、扭曲、汇聚、挤压和越山加速等情况,如图13所示。对于工况1和工况3,由于来流经过较高的山体时发生了山顶阻挡现象,而主梁刚好位于山体背风侧,因此部分位置的平均风剖面在低海拔处出现了减速情况。以工况1中主梁3/4跨处的平均风剖面为例,从图17显示的主梁流线图上可以清楚的看到,在主梁的3/4跨附近(图中箭头一侧),来流受到河岸突出的山体阻挡而发生跨越,当来流到达主梁时刚好处于山顶背风侧附近,因此风速发生了明显的减速作用。
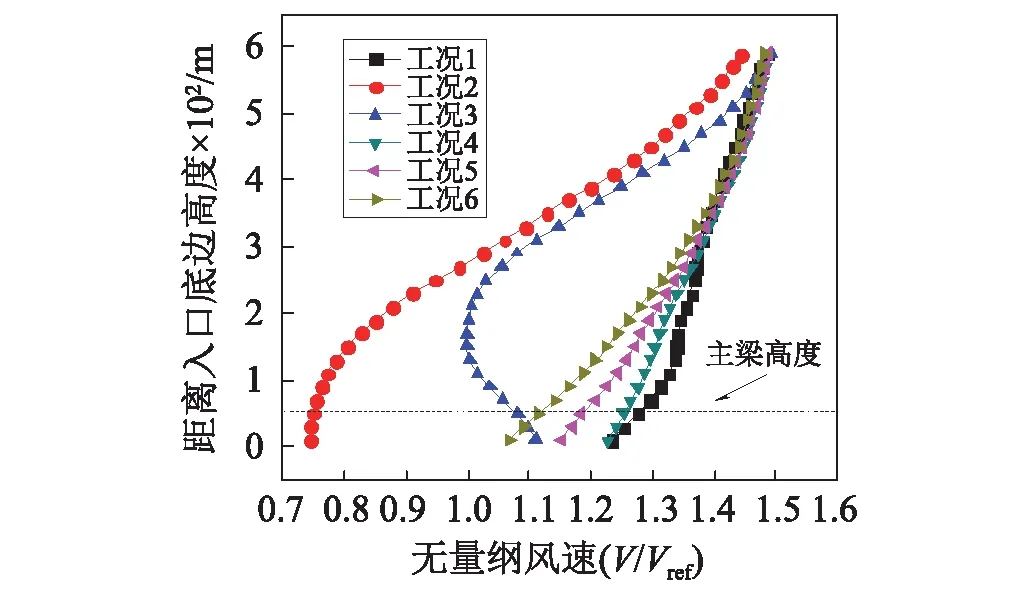
图14 主梁1/4跨处风速沿高度变化Fig.14 Variation of wind speed with height at 1/4 span
随着高度的增加,地形的影响因素也渐渐地变小,平均风速总体也呈现出随高度增加而增大的现象,并趋向于指数律分布形式,这也说明数值模拟的计算域设置合理,计算域顶部边界对内部流场的影响很小。
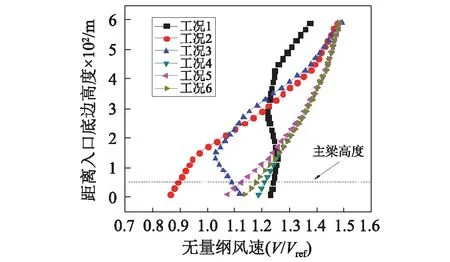
图15 主梁跨中风速沿高度变化Fig.15 Variation of wind speed with height at mid span
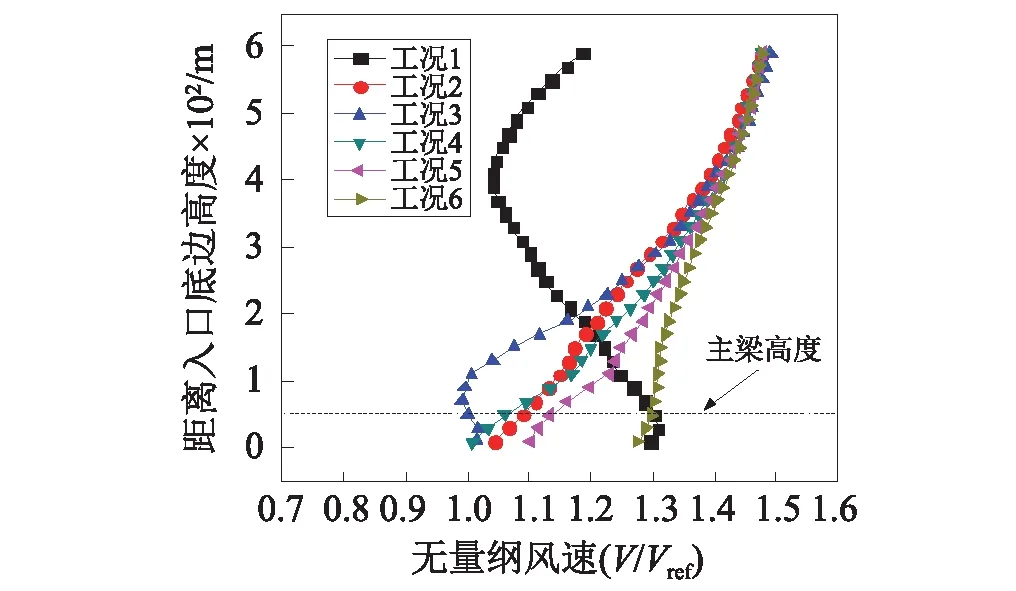
图16 主梁3/4跨处风速沿高度变化Fig.16 Variation of wind speed with height at 3/4 span

图17 工况1的主梁流线图(左侧为风速入口)Fig.17 Streamline of case 1 (inlet on the left)
2.3 主梁风攻角和风向角分布
风攻角是影响主梁截面气动力的重要参数,也是桥梁抗风设计的重要依据。图18为不同工况下主梁上的风攻角分布情况。总体上看,桥梁主梁的前半段风攻角较小,后半段风攻角较大。这是因为前半段的海拔较低,地势相对平缓,后半段的海拔较高且地势起伏大,并且桥梁主梁距离地面相对较近,因此当气流经过时会受到较为显著的地形影响,产生较大的风攻角。当河道上游来流时,工况1、工况2和工况3的正负风攻角相对较大,正攻角最大约+10°,负攻角最大约-9°,说明气流经过主梁时,会分别产生向下和向上的气流。从图19中工况3的主梁流线图上看到,主梁流线有两股汇聚而成。受上游山体分割,上半部分来流经过河道到达主梁,受河道地势的干扰,气流产生向上的流动趋势,因此产生了正攻角;下半部分来流越过上游山体到达主梁,下半段主梁刚好处在背风坡,因此产生了负攻角。而下游来流时,工况4、工况5和工况6均会产生较大的正攻角,说明气流在主梁处产生向上流动的趋势。从地形上看,气流从地势低处流向高处,主梁处在迎风坡,自然产生正风攻角。总之,山区峡谷桥址处的主梁风攻角变化非常复杂,局部地形对其有主导作用,因此在实际桥梁抗风设计时,还要结合具体桥址处周围的地形而确定,特别是当桥梁位于较为陡峭的地形时。
风向角也对桥梁安全有重要的影响,特别是桥梁建设阶段。图20列出了6个不同工况下的主梁风向角分布情况。由于地形高差相对不大,虽然有山体对气流产生阻挡作用,但距离桥位较远,气流绕过山体到达主梁时方向趋向一致,因此导致主梁处气流方向基本和来流方向一致,除了靠近右侧陡峭山体部分外,主梁上的风向角变化不是很大。因此,在该桥梁抗风设计时,需重点关注主梁右半部分的风向角影响,而左半部分按和来流方向一致处理即可。
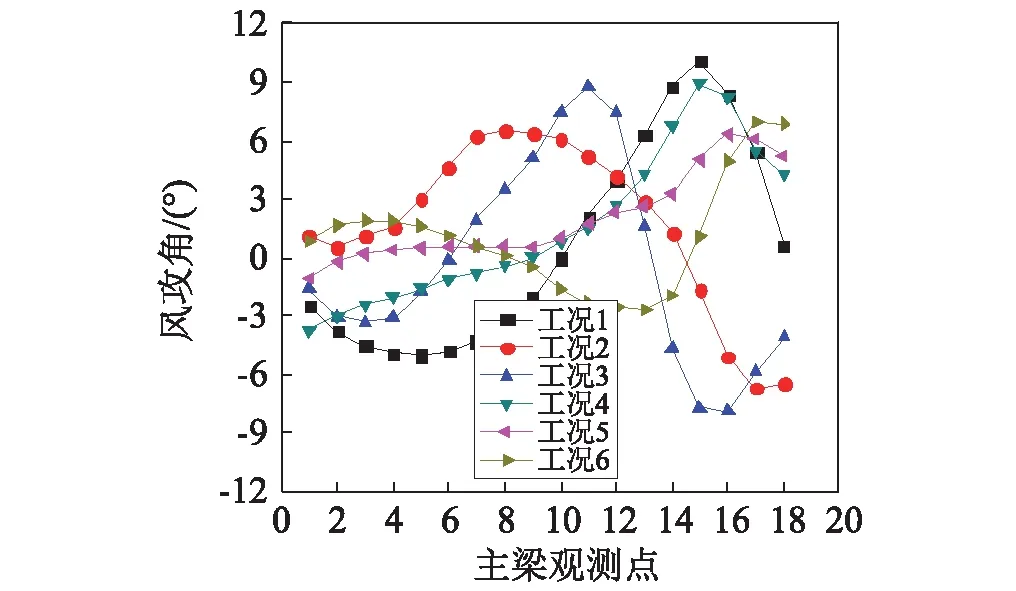
图18 主梁风攻角分布Fig.18 Distribution of wind attack angle

图19 工况3的主梁流线图(左侧为风速入口)Fig.19 Streamline of case 3 (inlet on the left)
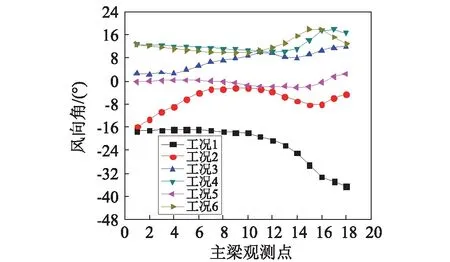
图20 主梁风向角分布Fig.20 Distribution of wind directional angle
2.4 风速放大系数
为了研究该桥址处河道峡谷对气流的加速作用,按式(4)定义了风速放大系数。图21为不同来流工况下,主梁上的水平风速放大系数分布情况。从图中可以发现,工况1和工况6的风速放大系数最大,其中最大值为1.303 2。其它工况的风速放大系数也较大,其中工况2的风速放大系数最小,在2.1节中分析了原因。由于该桥位处的河道较为平直,一定范围内河道几乎没有弯曲,同时地形起伏相对较缓和,海拔差距不是很大,所以不同工况下的风速放大系数较为一致。受河道和两岸山体的作用,气流发生汇聚加速,在主梁处产生了较大的风速放大系数。
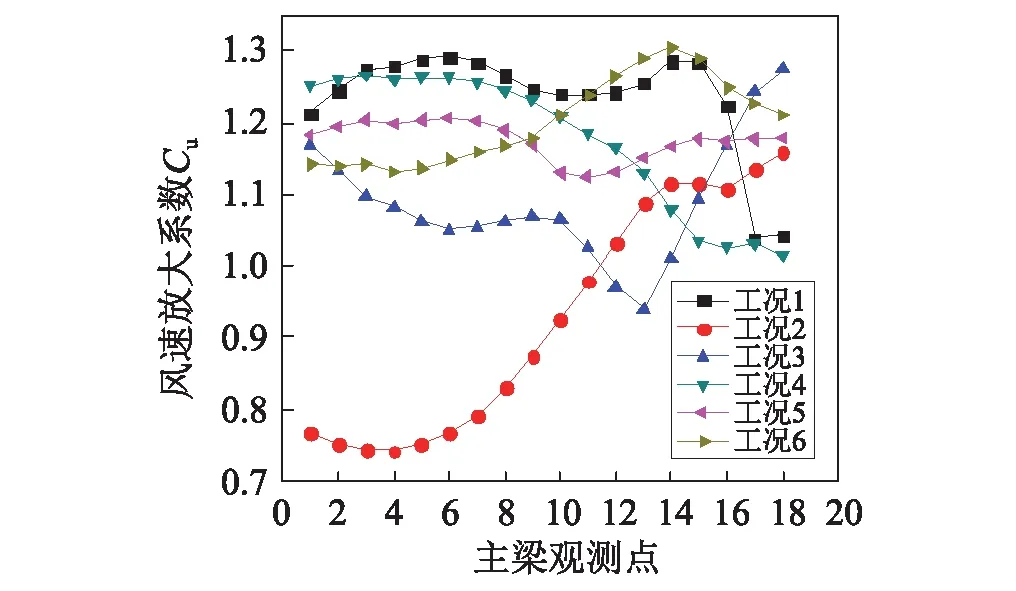
图21 主梁风速放大系数分布Fig.21 Distribution of speed-up factor
为了对比说明本文提出的数值模拟方法的正确性,另外采用了规范中的经验关系式(5)计算桥址处的山谷效应修正系数,其中假设大桥桥址“虚拟标准气象站”的基本风速为峡谷进口风速。由于该桥址河道较为规则,因此较适用经验公式计算峡谷效应修正系数。
(5)
式中:H为峡谷深度,一般桥梁建于峡谷上口处,可取主梁桥面至峡谷下底面高度;B1为峡谷上口处宽度,一般为主梁桥面长度;B2为峡谷下底面宽度;κ为山谷效应修正系数。
由于河道分为有水和无水两种情况,而本文CFD数值模拟计算的是无水情况,因此下面计算河道无水情况。根据式(5),其B1=680 m,B2=0,H=310 m,π=3.141 6,可得κ=1.286 4。CFD数值模拟得到的风速放大系数最大值为1.303 2,可得与峡谷效应修正系数κ=1.286 4的误差仅为1.3%,在一定程度上说明了本文提出的数值模拟方法的合理性和准确性。
3 结 论
本文以某在建的山区峡谷大桥桥址处风场为研究对象,提出了一种改进的山区峡谷地形风场数值模拟方法。该方法的计算域设计更为合理;地形边缘过渡段较为平缓,气流受到干扰较小,更符合实际流动情况;同时,利用“虚拟标准气象站”法获得了计算域入口风速条件,使得计算结果更加准确。通过分析主梁不同位置上的横桥向和顺桥向风速及其放大系数、风攻角、风向角和平均风速剖面等风场关键参数及其流动机理,得到了以下结论:
(1)本文采用的改进的山区峡谷地形风场特性CFD数值模拟方法,利用“虚拟标准气象站”法计算桥址处基本风速,并以此设计计算域入口指数风速剖面,同时设置地形过渡段等改进措施,是正确的、合理的。
(2)采用“虚拟标准气象站”法计算得到的桥址处基本风速为24.75 m/s。数值模拟结果显示,主梁上的横桥向风速沿桥跨变化较大,顺桥向风速沿桥跨变化较小;受山地地形的影响,风剖面已经不符合规范中规定的指数风剖面;该桥址处的主梁风攻角在-9°~+10°。
(3)数值模拟得到的主梁上的风速放大系数最大为1.303 2,同时根据规范中的经验公式得到的山谷效应修正系数为1.286 4,两者吻合较好,误差仅为1.3%。

