悬索桥双吊索尾流致涡激振动的大涡模拟
赵 燕, 林伟群, 杜晓庆,2, 杨 骁, 代 钦
(1. 上海大学 土木工程系,上海 200444; 2. 上海大学 风工程和气动控制研究中心,上海 200072;3. 上海大学 上海市应用数学和力学研究所,上海 200072)
双吊索在大跨度悬索桥上有着广泛的应用,下游索受到上游索尾流干扰会发生尾流激振现象[1]。Fujino等[2]将双索的尾流激振分为尾流致涡激振动、尾流驰振和尾流致颤振等振动类型。随着悬索桥的跨度不断增大,双吊索发生尾流激振的可能性大幅增大,因而双索的尾流激振研究受到众多学者关注[3-6]。
目前,研究者对双索的尾流驰振或尾流致颤振进行了较为深入的试验研究。杜晓庆等研究了错列双圆柱的尾流驰振,并发现了两种不同的振动形式。Fujino等研究了双索尾流驰振的起振条件。Li等研究了风攻角和双索间距对尾流驰振的影响等。肖春云等研究了双圆柱处于尾流的圆柱的平均气动力系数随空间位置的变化规律及发生尾流弛振的不稳定区间。
相对来说,目前对双索尾流致涡激振动的研究较少。杜晓庆等在研究了间距为4D(D为圆柱或双索的直径)的串列和错列双圆柱的尾流致涡激振动时发现,无论是错列还是串列布置,下游圆柱的尾流致涡激共振的振幅均远大于单圆柱涡激振动的振幅。Wong[7]研究了单圆柱及不同间距比、不同阻尼系数下各种串列圆柱组合的尾流致振。Brika等[8]设计了一套可使上下游圆柱同相位振动和反相位振动的试验装置,对串列和错列的双圆柱的涡激振动进行了研究。Kim等[9]对串列双圆柱的风致振动进行了风洞试验研究,并根据上下游圆柱的响应按照圆心间距划为五个区域。
随着流体力学理论和计算流体动力学的不断发展,近年来研究者尝试采用数值模拟方法来研究尾流致振问题。Carmo等[10]对串列双圆柱涡激振动进行了数值模拟研究。结果显示:当发生共振时,下游圆柱的振幅约为单圆柱时的2倍;下游圆柱在高折减速度下,有较大的振幅,这与同样情况下单圆柱的较低振幅不同。Mysa等[11]对雷诺数Re=100、质量比m*=m/(0.25ρπD2)≈2.6(m为圆柱的单位长质量,ρ为流体密度)的串列双圆柱尾流致涡激振动进行数值模拟,研究表明:流体力与结构响应之间的相位差在流体与结构之间的耦合中起着主要作用。Bao等[12]对串列双圆柱双自由度涡激振动进行了数值模拟,研究发现上下游圆柱同时发生共振现象在各个频率比下都会发生,且上游圆柱的振动情况与同样情况下的单圆柱的类似。郭晓玲等[13]对雷诺数Re=150的双圆柱进行了数值模拟,研究了质量比、圆心间距及折减速度对下游圆柱尾流致涡激振动的影响。
与试验相比,数值模拟方法更利于研究多圆柱风致振动的流固耦合机理。以往的数值模拟研究大多局限在低雷诺数(Re<200)的层流中进行的,而且计算大多采用二维数值模型,模型的质量比也较低(m*<20),这与双索的尾流致涡激振动的条件相差甚远。圆柱型结构的气动性能有强烈的雷诺数效应,为了揭示双索尾流致涡激振动发生的内在机理,有必要在高雷诺数(Re>1×104)下进行尾流致涡激振动数值模拟。
本文采用大涡模拟方法,在较高的雷诺数范围内(Re=1×104~4×104),以圆心间距为4D的串列双圆柱为研究对象,进行了尾流致涡激振动数值模拟,并与作者先前的试验研究结果进行比较,研究了下游圆柱的动力响应和气动力随着折减风速的变化规律,探讨了下游圆柱动力响应、绕流场特性以及气动力三者之间的耦合关系,考察了上游圆柱的尾流对下游圆柱的影响方式。
1 数值方法
1.1 湍流模型的选择
目前湍流数值模拟方法主要分为三种:直接数值模拟(Direct Numerical Simulation,DNS)、雷诺平均法(Reynolds Average Navier-Stokes,RANS)和大涡模拟(Large Eddy Simulation,LES)。DNS方法可以获得湍流场的精确信息,但现有的计算资源往往难以满足对高雷诺数流动模拟的需要。RANS方法可以计算高雷诺数的复杂流动,但只能给出平均运动结果。LES方法采用瞬时的N-S方程直接模拟湍流中的大尺度旋涡,而小尺度旋涡可以通过近似模型来考虑。与DNS法相比,LES法可以节约计算机资源。与RANS法相比,LES法可以更准确地模拟圆柱的边界层分离、涡的形成及其发展过程,因而本文采用LES方法。
绕流问题中黏性流体不可压连续方程和瞬时N-S方程滤波整理后,为[14-16]
(1)
(2)
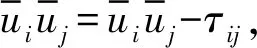
(3)
构造亚格子应力τij的Smagorinsky-Lilly封闭模式为
(4)
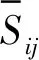
亚格子Smagorinsky-Lilly模型中的亚格子湍流黏性系数为
(5)
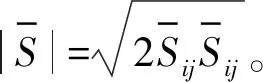
Ls=min(κd,CsV1/3)
(6)
式中:κ为Von Karman常数;d为到最近壁面的距离;Cs为Smagorinsky常数; 本文计算中Cs取0.1;V为计算单元的面积。
1.2 结构控制方程
考虑图1所示上游圆柱固定、下游圆柱可作顺风向和横风向的运动的双圆柱系统,并将下游圆柱等效为质量-弹簧-阻尼系统,其两自由度振动方程为
(7)
(8)
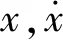

图1 双圆柱计算模型示意图Fig.1 Computational model of two circular cylinders
本文的数值模拟圆柱与流场之间的流固耦合作用,是通过动网格技术来实现的,其步骤如下:
步骤1运用大涡模拟方法求解流体控制方程,获得流场速度场、压力场和下游圆柱表面的流体力;
步骤2将流体力作用于下游圆柱,以四阶Runge Kutta法求解下游圆柱运动控制方程式(7)和式(8),得到下游圆柱横风向和顺风向的动力响应;
步骤3通过动网格技术,将下游圆柱的速度传递于网格系统,更新网格位置;
步骤4返回步骤1开始计算下一个时间步的响应,如此循环可得各时间步的下游圆柱动力响应,实现上述流固耦合算法。
1.3 网格划分及计算参数
计算域与网格划分如图2和图3所示。将计算域分块进行网格划分,在双圆柱附近采用圆形网格划分,并在靠近圆柱表面处进行加密。所有工况的圆柱近壁面的0.35D的厚度内采用结构化网格,如图3所示。下游圆柱在图2所示的设置为界面(interface)边界的圆形流域内运动,其他区域为静止区域。
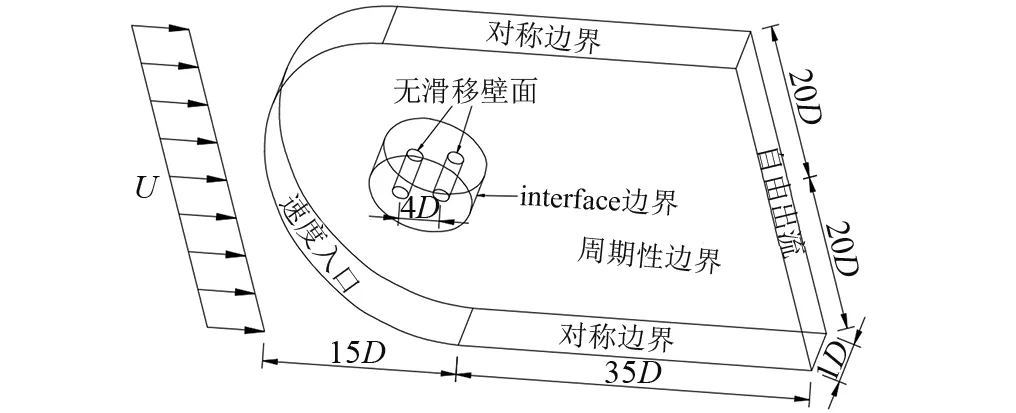
图2 计算域和边界条件Fig.2 Computational domain and boundary conditions

图3 计算网格Fig.3 Computational grid
针对圆心间距为4D的串列圆柱尾流致涡激振动,采用杜晓庆等的风洞试验相关的参数:圆柱直径D=0.18 m,雷诺数为1×104~4×104,折减风速Ur=3~10,在静止空气中的自振频率fn=1.73 Hz。由于大涡模拟的计算量较大,为了减小起振时间,降低计算量,阻尼比取0,质量比m*取40。

压力和速度耦合采用SIMPLEC法求解,动量方程和湍动能耗散率方程采用二阶精度的离散格式。无量纲时间步长Δt*为0.005(Δt*=ΔtU/D, 其中Δt为非定常计算时间步长)。
边界条件设定:入流面采用速度入口(velocity-inlet)边界条件;出流面采用自由出流(outflow)边界条件;顶面和底面采用对称(symmetry)边界条件;两侧面(圆柱展向两端的平面)采用周期性(periodic)边界条件;串列圆柱表面采用无滑移壁面(wall)边界条件;圆柱体的运动区域与静止区域之间的交界面采用界面(interface)边界条件。
2 计算结果及分析
2.1 计算结果验证
为了保证本文所采用的计算方法和网格模型的可靠性,以固定单圆柱为研究对象进行结果验证。在雷诺数为4×104时,分析了周向网格数量和展向网格数量对计算结果的影响,并将计算结果与文献内的风洞试验和数值模拟结果进行了比较。
表1列出了本文计算得到的平均阻力系数、脉动升力系数和Strouhal数(St)等结果与文献结果的比较,而图4和图5给出了本文计算得到的圆柱表面平均风压系数和脉动风压系数与文献值的比较。
从表1、图4和图5可知:随着周向网格从120增加至256,本文的三个工况A1,A2和A3的风压系数、气动力系数和St数较为接近,体现了本文计算结果的网格独立性;而这三个工况的数值与文献结果相比发现,St数较为吻合,但平均阻力、脉动升力和表面风压系数有一定的偏差。为了验证展向网格对结果的影响,A4工况在A2工况的基础上,将展向的网格数量从10个增加至15个,由表1、图4和图5可知,A4工况的气动力系数和表面风压系数更为接近于文献值。这说明增加展向的网格数量可以提高计算的精度。但限于计算资源,下文仍参考A2工况的计算参数和网格来建立尾流致涡激振动的计算模型。
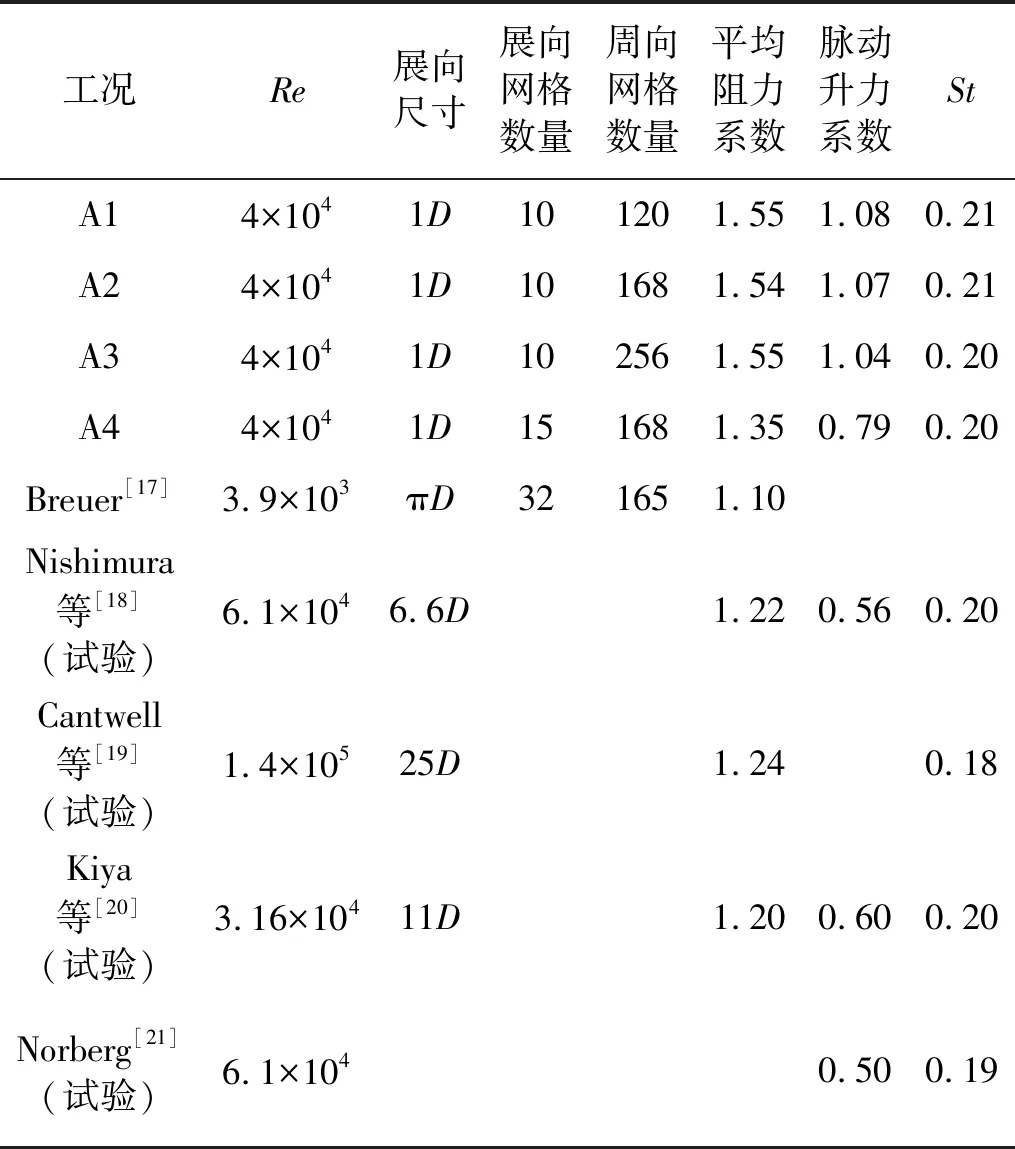
表1 静止圆柱的确定与验证
图6给出了串列双圆柱的尾流模态图,在振幅较小、折减风速较低的Ur=3.0情况下,下游圆柱的尾流呈现出“2S”的模态(“2S”的模态,即:每半个振动周期从下游圆柱脱落单个旋涡);在振幅较大的Ur=5.8时,下游圆柱的尾流呈现出“2P”的模态(“2P”的模态,即:每半个振动周期从下游圆柱脱落一对旋涡)。这与文献[22]的试验结果相吻合,再次验证了计算结果的正确性。
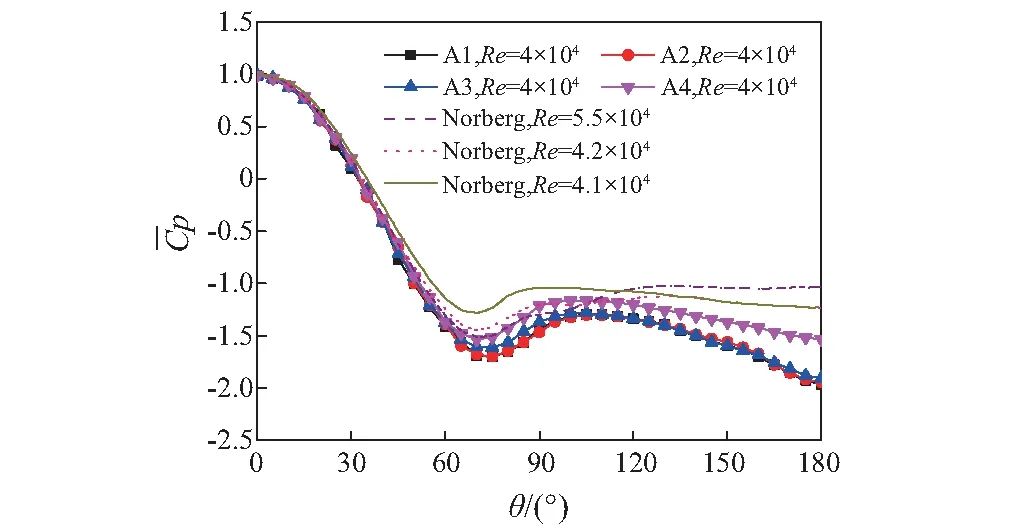
图4 平均风压系数Fig.4 Mean pressure coefficient
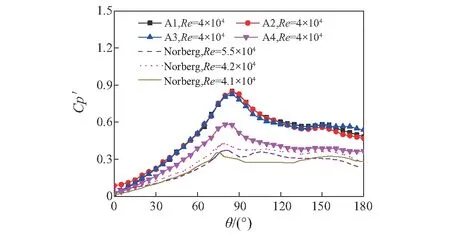
图5 脉动风压系数Fig.5 RMS pressure coefficient

图6 Ur=3和Ur=5.8的串列双圆柱的尾流模态Fig.6 Wake mode of tandem cylinders under Ur=3 and Ur=5.8
2.2 动力响应特性
图7为下游圆柱的振幅随折减风速的变化曲线,图7也给出了杜晓庆等研究中的风洞试验结果。本文中所提到的振幅指的是无量纲化的振动幅度的最大值。其中,xmax/D,ymax/D分别为顺风向和横风向的无量纲化的最大振幅。
由图7可知,下游圆柱的振动主要发生在横风向,下游圆柱的顺风向的振幅较小,振幅随折减风速的变化趋势与风洞试验结果相似,这说明数值模拟结果与试验结果吻合良好。
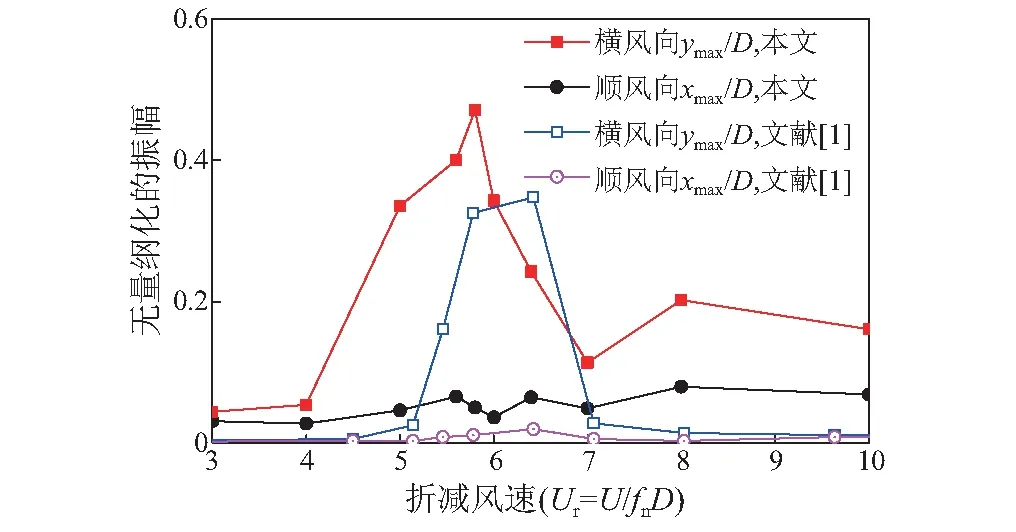
图7 振幅随折减风速的变化情况Fig.7 Variation of the amplitude with the reduced velocity
本文的计算工况在折减风速Ur<5时,下游圆柱的振动幅值较小,还未进入涡激共振区;随着折减风速的进一步着增大,振幅开始有明显增大,在Ur=5.0时,振幅达到0.35D; 当折减风速Ur=5.8时,下游圆柱的横风向的振幅达到最大值,约为0.47D;随着折减风速的进一步增大,圆柱的横风向的振幅开始减小。其中,共振发生在Ur=5.0~7.0。
而文献[1]的最大振幅发生在Ur=6.0时,最大振幅达到0.35D,共振发生在Ur=5.5~7.0。相比而言,本文的计算工况在横风向发生共振的折减风速范围和最大振幅均较大,最大振幅发生的折减风速较小。这可能是由于本文所采用的质量比和阻尼较文献[1]小的缘故。
图8为Ur=5时下游圆柱的横风向的位移y/D的时程曲线。其中,y/D为无量纲化的横风向位移。圆柱的横向振动过程可以观察到“拍”的现象,而对于Ur<5及Ur≥7的工况,则没有“拍”的现象。“拍”是涡激振动的一个重要的特征,是由于圆柱的固有频率与涡激振动频率相近而产生的共振不稳定导致的。
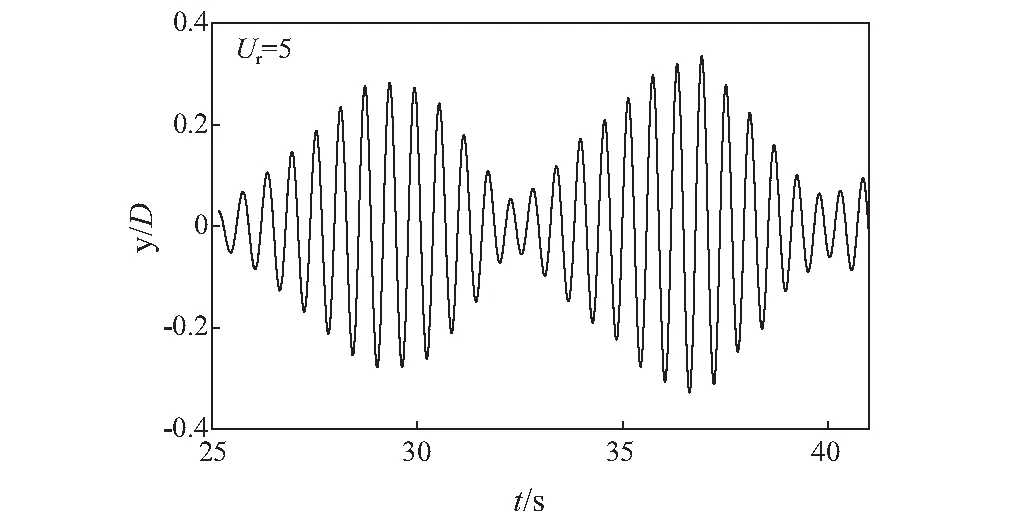
图8 “拍”现象Fig.8 The “beat” phenomenon
2.3 气动力特性
图9给出了下游圆柱的横风向的振幅ymax/D、平均阻力系数CD2,mean和脉动升力系数CL2,rms随折减风速的变化曲线。图中也给出了本文对雷诺数为40 000的固定的圆心间距为4D的串列双圆柱的大涡模拟的计算结果,即下游圆柱的平均阻力系数CD2,mean-sta和脉动升力系数CL2,rms-sta。
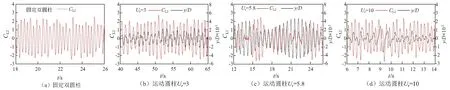
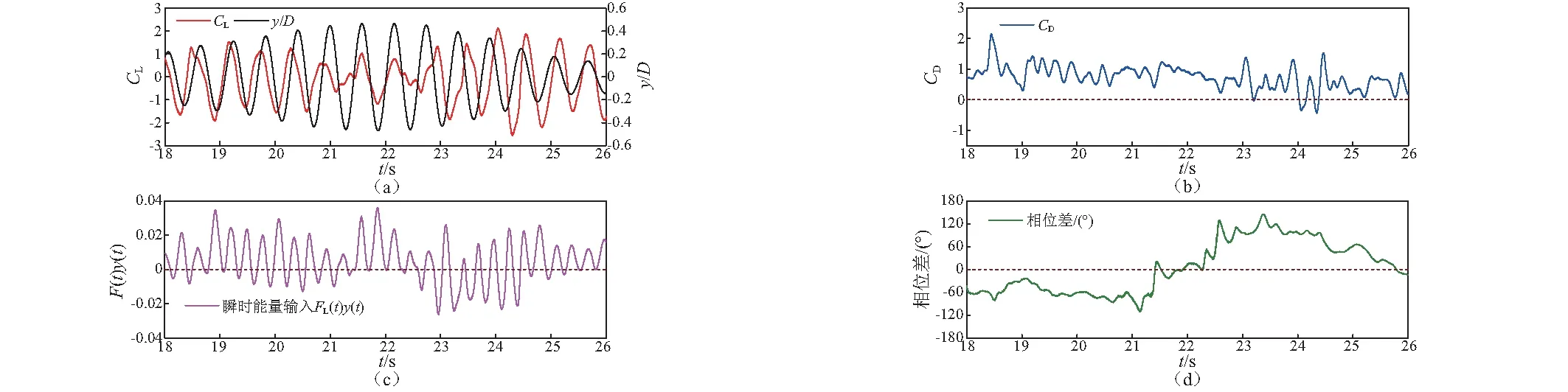
从图9可知,横风向振幅较小时(在Ur<5和Ur≥7时),带两自由度的下游圆柱的平均阻力系数基本与固定圆柱的结果较为接近。而在发生大幅涡激振动时(5 当Ur=3和Ur=10时,随着时间的推移,下游圆柱的升力系数的幅值变化与固定双圆柱的基本类似,且升力系数的幅值大于1;而当Ur=5.8时,随着时间的推移,升力系数的幅值时而增大至与图10其他工况变化类似,时而减小至幅值小于1(图10(b)中t=13.5~14.5 s附近),其波动与图10中的其他的工况相比,较为明显。Ur=5.8工况的这种随时间变化,升力系数时而增大时而减小,可能是造成Ur=5.8的脉动升力系数并没有显著增大的原因。另外,从图10(b)可知,在Ur=5.8时,随着下游圆柱瞬时的横风向的位移的增大,脉动升力系数反而减小,这是由于气动力与位移之间的相位差造成的。 图9 气动力和最大振幅随折减风速的变化情况Fig.9 Variation of the maximum amplitude and aerodynamic forces with the reduced velocity 为了进一步解释脉动升力系数的特点,图10给出了固定的串列双圆柱的下游圆柱的升力系数的时程曲线及三个典型计算工况(Ur=3,5.8,10)的下游圆柱的横风向位移及升力系数的时程曲线。 图11给出了在Ur=5.8时,下游圆柱的气动力系数、振幅、瞬时的能量输入(其中,正值代表气动力对结构做功,负值代表气动力消耗结构的能量,FL(t)代表瞬时的气动升力,y(t)代表瞬时的横风向位移)、采用希尔伯特变换[23]得到的横风向的位移与气动升力的相位差的时程曲线(其中,正值代表横风向位移的瞬时相位滞后于气动升力,负值代表横风向位移的瞬时相位领先于气动升力)。 图10 气动力和位移时程曲线Fig.10 Time history of the displacement and the lift 由图11的瞬态能量输入图可以看出:对于高雷诺数的串列双圆柱的涡激振动,下游圆柱的气动力对下游圆柱输入能量或者消耗下游圆柱的能量,这会引起下游圆柱的气动力与振动之间产生不稳定的相位差,同时,相位差对下游圆柱的振幅的变化也有重要影响。 当尾流致涡激振动发生时,在下游圆柱的横风向的振幅逐渐增大过程中,位移的瞬时相位领先于升力,在一个振动周期内升力对下游圆柱做正功,而位移与升力之间的相位差则逐渐增大;反之,下游圆柱的横风向的振幅逐渐减小时,位移的相位滞后于气动升力,在一个振动周期内气动升力对结构系统做负功,下游圆柱的气动阻力系数出现负值,气动升力与位移间的相位差也随之减小。 图11 Ur=5.8时的位移、气动力系数的时程曲线及能量输入模式及相位差Fig.11 Time history of displacement and aerodynamic force coefficients, energy input mode and the phase difference between the displacement and the lift under Ur=5.8 在工况Ur=5.8的两个连续的振动周期内选取如图12所示九个不同典型时刻可知,两个振动周期包含了振幅达到最大及开始减小的过程。图13为图12中T1~T9的典型时刻的瞬态涡量图。其中,图13中的“1”、“2”、“3”、“4”代表上游圆柱依次脱落的旋涡的编号。 图12 Ur=5.8时的位移、气动力系数的时程曲线Fig.12 Time history of displacement and aerodynamic force coefficients under Ur=5.8 从图13(a)~图13(f)可知:“1”号旋涡在T2时刻自上游圆柱脱落后,在T4时刻,由于下游圆柱偏离平衡位置相对较远,旋涡从下游圆柱的外侧流经,并与下游圆柱的剪切层发生相互作用。在T1~T5时刻,气动升力与位移之间基本是属于同相位,同时振幅在T2时刻达到最大。 从图13(a)~图13(i)可知:“2”、“3”和“4”号旋涡自上游圆柱脱落后,分别在T6、T7和T9时刻时,直接撞击到下游圆柱的表面,这是由于下游圆柱在平衡位置附近。不同时刻撞击的位置也不同,并与下游圆柱不同位置的剪切层(取决于上游圆柱的旋涡撞击到下游圆柱表面的位置)发生作用。从T5~T9时刻的推移,气动升力与位移之间的相位差有明显增加,振幅逐渐减小。 综上,在来流的作用下,上游圆柱的上下两侧会形成交替脱落的旋涡,它们对下游圆柱的影响有上述两种不同的方式。其中,上游圆柱的旋涡撞击到下游圆柱的表面的这种影响方式对下游圆柱的气动力和位移之间的相位差影响较大。 图13 Ur=5.8时不同时刻的涡量Fig.13 Vorticity at different moments under Ur=5.8 本文采用CFD(Coputation Fluid Dynamics)大涡模拟方法及动网格技术,对串列双圆柱尾流致涡激振动的流固耦合机理进行了研究。主要结论如下: (1) 大涡模拟得到的振动响应与文献中的趋势类似,在尾流致涡激振动的锁定区域,横风向的振动响应能很好地捕捉到“拍”的现象,尾流的模态也与文献结果一致。表明数值模拟结果与试验结果吻合良好,在高雷诺数下采用大涡模拟分析双圆柱尾流致涡激振动问题可获得可靠的结果。 (2) 在不同的折减风速下,带两自由度的下游圆柱的平均阻力系数与其振幅的变化趋势相同,即下游圆柱的平均阻力系数随着最大振幅的增加而增大,但下游圆柱的脉动升力系数没有这样的变化趋势,这是由于气动力与位移之间的相位差造成的。 (3) 当尾流致涡激振动发生时,在下游圆柱的振幅增大的过程中,位移的瞬时相位领先于气动升力,在一个振动周期内气动力对下游圆柱做正功,下游圆柱的位移与气动升力的相位差逐渐增大;反之,在下游圆柱的振幅逐渐减小的过程中,位移的相位相对于气动升力的相位滞后时,气动力对下游圆柱做负功,下游圆柱的位移与气动升力的相位差逐渐减小。 (4) 上游圆柱的尾流对下游圆柱的影响有两种不同的方式,一种是当下游圆柱偏离平衡位置较远时,从上游圆柱脱落的上游圆柱脱落的旋涡从下游圆柱的外侧流经,与下游圆柱的剪切层发生相互作用;另外一种是当下游圆柱在平衡位置附近时,上游圆柱的漩涡则直接撞击到下游圆柱的迎风面,不同时刻撞击的位置也不同。 需要指出的是,本文仅考虑了两个圆柱和来流处在同一直线上的串列布置双圆柱的尾流致涡激振动,实际吊索会受到来自不同风向的来流作用,还需考虑风向角对尾流激振的影响。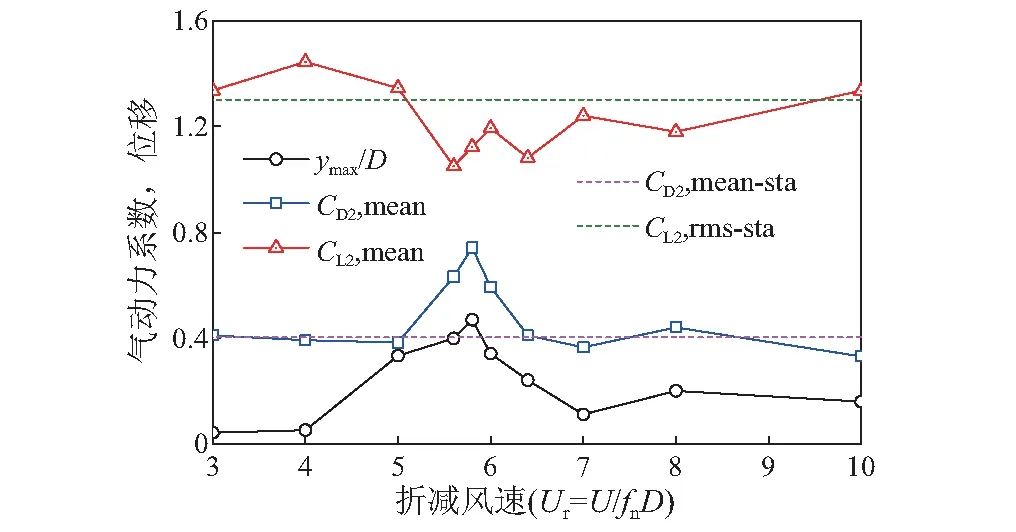
2.4 气动力与振动响应关系
2.5 尾流干扰模态


3 结 论

