旋转镗杆切削颤振稳定性预测

马伯乐， 任勇生， 张玉环， 张金峰

(山东科技大学 机械电子工程学院，山东 青岛 266590)

随着现代航空制造业的发展，关键零部件的设计制造过程中，经常会遇到超长径比复杂深孔的加工问题，其加工精度和表面质量等性能对航空业的发展具有重要的作用。深孔加工方法主要包括深孔钻削、深孔铰削、深孔镗削和深孔铣削等。其中，深孔镗削作为一种提高深孔加工精度的有效加工方法，得到了广泛的应用。然而，随着对航空发动机性能的不断改进，零部件的长径比不断增大，使得用于深孔加工的镗刀刚度变差，极易发生颤振，造成工件的加工精度和表面加工质量降低，同时降低了刀具和机床寿命。因此，为了为有效抑制加工颤振和提高加工精度提供理论依据，精准地预测镗削过程的稳定性就变的尤为重要。

由振纹再生效应引发的颤振是切削颤振中的一种主要的形态。Altintas等[1-2]采用频域法分析和预测了铣削颤振边界以及稳定性极限切削深度，但上述研究并未考虑主轴旋转产生的陀螺效应的影响。Mosaddegh等[3-4]基于有限元模型分析陀螺效应下的铣削颤振，在计算耳瓣图时采用的迭代法。Arvajeh等[5-7]建立旋转二自由度钻杆切削过程模型，并应用频域法研究钻削过程的稳定性。然而，无论是铣削还是钻削过程，其切削力模型都不适用于镗削过程，所以，对于镗削动力学建模及其切削稳定性问题需要进一步的研究。

Atabey等[8-9]研究了镗削过程的力学原理，并提出了镗削力系统的数学模型。Ozlu等[10-12]提出了预测镗削力的方法，数值模拟与实验测试结果进行了比较，验证了镗削力模型的合理性。石建飞[13]建立了二自由度、三自由度减振镗杆系统模型，研究了系统动力学参数对振动特性的影响，但上述研究没有对镗削过程的颤振问题进行分析。Pratt等[14]对再生切削条件下悬臂镗杆颤振控制问题及稳定性进行了分析。Baker等[15]对二自由度不对称镗杆的动力学模型进行了稳定性分析。Parsian[16]对多齿镗削系统进行建模、稳定性分析和频域仿真，最后通过实验验证了镗削模型的正确性。Ozlu等提出了一种用于镗削过程稳定性的分析模型。该模型不仅包含了多维形式，而且考虑了刀具切削时的几何形式，并分析出插入刀尖半径对稳定性极限的影响。为了提高镗杆的稳定性，Fallah等[17]研究了带有TMD的镗杆，采用频域法分析和预测了二自由度的动力学模型的切削稳定性。Selmi等[18]基于耦合导纳法研究多阶梯形镗杆切削过程的稳定性。庄润雨[19]基于Euler-Bernoulli梁理论建立再生颤振时静止镗杆的单自由度动力学模型，研究外阻对稳定性的影响。Li等[20]将旋转镗杆简化为二自由度系统，并且考虑内阻的影响，研究镗削系统的颤振特性，得到镗削加工过程的稳定性叶瓣图。

从上述研究报道可以发现，目前对于镗削过程建模，大多限于工件旋转、镗杆静止的情形，很少考虑旋转镗杆建模与切削稳定性研究；此外，现有的金属镗杆研究或者只考虑外阻的影响，或者只考虑内阻的影响，很少见到同时考虑外阻和内阻影响的研究报道。本文将镗杆简化为x-y二自由度动力学分析模型，进一步引入旋转镗杆的陀螺效应和离心效应，结合镗杆镗削力模型并且同时考虑镗杆内、外阻尼的影响，建立了镗杆切削系统的颤振分析模型。导出旋转镗杆的传递函数，利用频域法研究考虑镗杆陀螺效应的颤振稳定问题，对其临界切削深度给出预测。由于在模型中考虑了固有频率随主轴转速的变化，所以在计算耳瓣图曲线时不需要再进行主轴转速迭代，因此，提高了颤振稳定性计算的效率。根据镗削参数和机床振动系统的动力学参数，通过公式推导及Matlab仿真，得到镗削系统的稳定性曲线，最后通过时域数值积分验证了镗削稳定性叶瓣图计算结果的正确性。通过变参分析，研究了旋转陀螺效应、内阻、外阻、镗杆弯曲刚度以及切削刚度的影响，为镗削加工颤振稳定性设计提供理论依据。

1 镗削过程的动态模型

镗杆的主体结构可以简化为Euler-Bernoulli悬臂梁模型，即只考虑梁的横向振动。根据Hamilton原理(或者Lagrange方程)，能够建立其横向振动方程。而旋转陀螺项可通过动能表达式引入。如果进一步假设镗杆具有连续分布的内黏滞阻尼，采用Kelvin-Voigt黏弹性模型对其进行描述，则它的影响可借助于Rayleigh耗散函数引入系统。采用近似求解方法，可将上述横向振动方程简化为集中质量-弹簧-阻尼一维振动方程，考虑到镗杆存在两个方向上的横向振动，进而可扩展为x-y二维动力学模型。

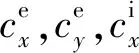
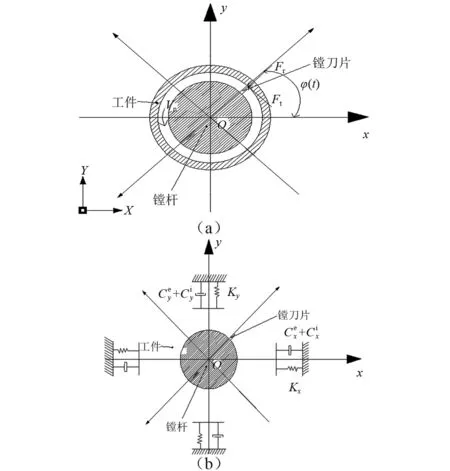
图1 镗削颤振系统动力学模型Fig.1 Dynamic model of boring chatter system

镗削过程的运动方程可以写成

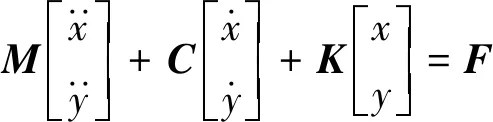
(1)

式中：M，C，K和F分别为质量、阻尼、刚度矩阵和作用在镗杆上的切削力。

(2)

式中：Ω为刀具的转速。

2 镗削力模型

由于镗削时的轴向分力变化量与切向、径向分力变化量相比较时小的多，因此在本文的镗削力模型中忽略了轴向分力，将镗削力简化为二维切削模型。图2为受力分析图。

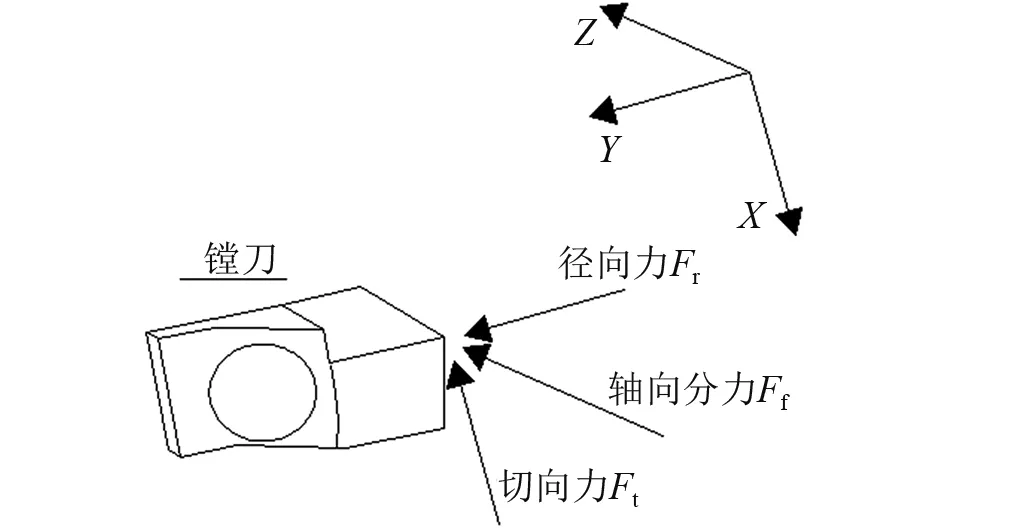
图2 镗刀受力分析图Fig.2 Force analysis chart of boring cutter

作用于镗杆的切向(Ft)和径向(Fr)切削力与轴向切削深度(a)和切削厚度(h)成正比

Ft(t)=Ktah(t),Fr(t)=KrFt(t)

(3)

切削系数Kr和Kt是不变的， 在x和y轴方向分解切削力为

(4)

在模型中，镗削力使刀具在x,y方向上会产生相应的动态位移。动态位移在沿切削厚度方向的大小为

h(t)=Δx(t)sinφ(t)+Δy(t)cosφ(t)

(5)

式中： Δx(t)=x(t)-x(t-T)； Δy(t)=y(t)-y(t-T)。

切削力式(3)和切削厚度式(5)代入式(4)，得到矩阵形式的结果为

(6)

由式(7)可以得出动态镗削力系数

(7)

式中：B1=FrFt，B2=Ft，φ(t)=2φ(t)。

考虑到主轴旋转，刀角位置随时间和角速度的变化，可以用式(8)来表示式(6)

(8)

式中： {Δ(t)}=[Δx(t),Δy(t)]T。

当镗杆旋转时，其定向因素随时间变化，[A(t)]为周期性函数，故可将[A(t)]展开为傅里叶级数，即

(9)

对[A(t)]进行谐波分析，[Ar]为其谐波(r=0,1,2,3,…)，则可用[A0]近似表示[A(t)]

(10)

引入变化的变量φs(t)=Ω(t+T)，φp(t)=ΩT，[A0]是在(0,2π)的时间间隔内得到的，所以[A0]表达为

(11)

其中，矩阵中的每一项积分表达式为

可将式(8)的镗削力表达为

(12)

式中： [A0]不随时间发生变化，而由径向切削深度以及相关的切削力系数确定。

3 求解方法

镗杆在镗削力作用下的运动方程为

(13)

对式(13)进行拉普拉斯变换，令s=σ+iω，s的取值与系统稳定性有如下关系：σ>0，系统处于不稳定状态；σ<0，系统处于稳定状态；σ=0，系统处于稳定与不稳定的临界状态： 取σ=0， 将s=iωc代入式(13)的拉普拉斯变换式，得

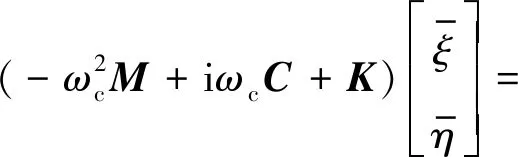
(14)

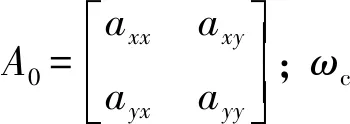
镗杆的传递函数为

(15)

具体写出如下

(16)

其中，

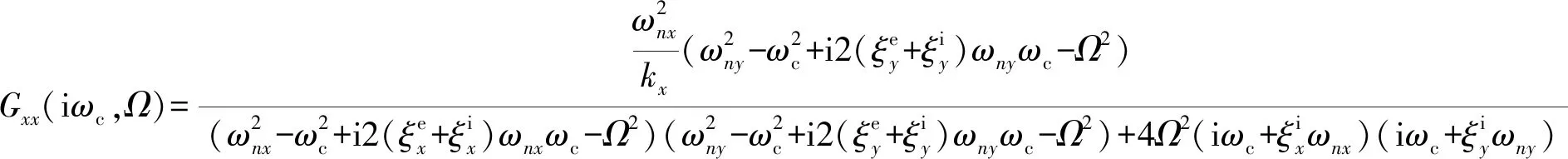
式(14)可以转化为

(17)

对应的特征方程为

(18)

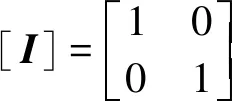
动态镗削的稳定性可以转为下列特征值问题，从而得到依据系数的二阶特征方程

(19)

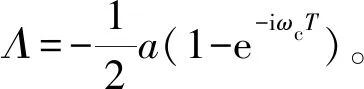
令：

(20)

将矩阵的行列式展开，化简得

a0Λ2+a1Λ+1=0

(21)

其中，

a0=[axxGxx(iωc,Ω)+axyGyx(iωc,Ω)][ayxGxy(iωc,Ω)+

ayyGyy(iωc,Ω)]-[axxGxy(iωc,Ω)+axyGyy(iωc,Ω)]×

[ayxGxx(iωc,Ω)+ayyGyx(iωc,Ω)];

a1=[axxGxx(iωc,Ω)+axyGyx(iωc,Ω)][ayxGxy(iωc,Ω)+

ayyGyy(iωc,Ω)]。

求解方程得

(22)

由于在计算G0(ω,Ω)时存在虚数i， 所以在Λ中存在虚部，则

Λ=ΛR+iΛI

(23)

由欧拉公式得

e-iωcτ0=cos(ωcτ)-i sin (ωcτ)

(24)

则得

(25)

可以解出

(26)

对分式分母有理化

(27)

由于镗削过程的极限切削深度是实数，因此，式(27)得到极限切削深度的虚部应是零，即

(ΛI(1-cos(ωcτ))-ΛRsin(ωcτ))=0

(28)

由此解得

(29)

最后，临界轴向切削深度(alim)的解析公式为

alim=-ΛR(1+κ2)

(30)

由式(27)，得

(31)

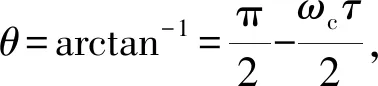
ωcτ=ε+2jπj=0,1,2

(32)

主轴转速

(33)

稳定极限图计算步骤：

步骤1求解或通过试验获得机床-刀具-工件和铣削过程的系统动态特性，即得出Wnx，Wny，Kx，Ky，ξx，ξy，Kt，Kr，Ks，Nt；

步骤2输入转速Ω，(本文的循环范围为0～20 000 r/min)；

步骤3以固有频率为参考，扫描颤振频率ωc，根据式(16)的出传递函数；

步骤4根据式(23)求解出实部与虚部，通过式(30)求解出临界轴向切削深度(alim)；

步骤5选择r阶模态下的临界轴向切削深度，取Ω对应的临界轴向切削深度(alim)；

步骤6最后以临界轴向切削深度(alim)深为稳定性极限图的纵坐标，以主轴转速为横坐标，绘制曲线。

4 数值结果与分析

本文算例中选取参数的数据，材料的力学特性如表1所示。

表1 材料力学特性

4.1 考虑旋转影响的固有频率变化曲线

旋转陀螺效应使得系统的固有频率和随着转速的变化而变化，当取式(13)右端为0，可以求得固有频率随转速的变化规律。从图3可以得出结论：当考虑陀螺效应时，主轴转速的变化将系统的固有频率分成上下两个分支，即向前和向后涡动频率，其中，向前涡动频率随着转速的增加而增加，向后涡动频率随着转速的增加而减小。

4.2 镗削颤振稳定性叶瓣图的验证

图4和图5给出未考虑陀螺效应的稳定性叶瓣曲线和选取的10个点的时域响应图。选取分析第3瓣曲线附近的3个点1，2，7。其中1点和2点具有相同切削宽度b=0.3 mm，但主轴转速不同的时间响应曲线。其中1点和7点具有主轴转速，切削宽度不同的时间响应曲线。响应曲线采用Matlab中求解延迟微分方程的命令dde23进行求解。由图3表明，1点是转速为6 000 r/min，切削宽度b=0.3 mm，其切削过程是不稳定的，此时的点位于叶瓣曲线以内的区域，即不稳定切削区域；2点是转速为7 000 r/min，切削宽度b=0.3 mm，其切削过程是稳定的，此时的点位于叶瓣曲线以外的有条件稳定切削区域；7点是转速为6 000 r/min，切削宽度b=0.2 mm，其切削过程是稳定的，此时的点位于叶瓣曲线以外的无条件稳定切削区域。其余点的时域响应图见图5。

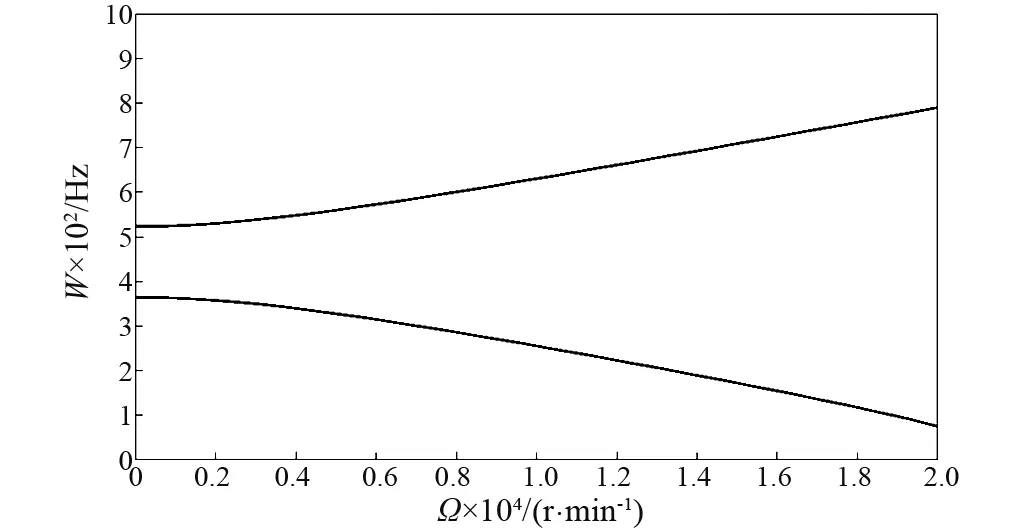
图3 固有频率随转速变化图Fig.3 Change diagram of natural frequency with rotational speed

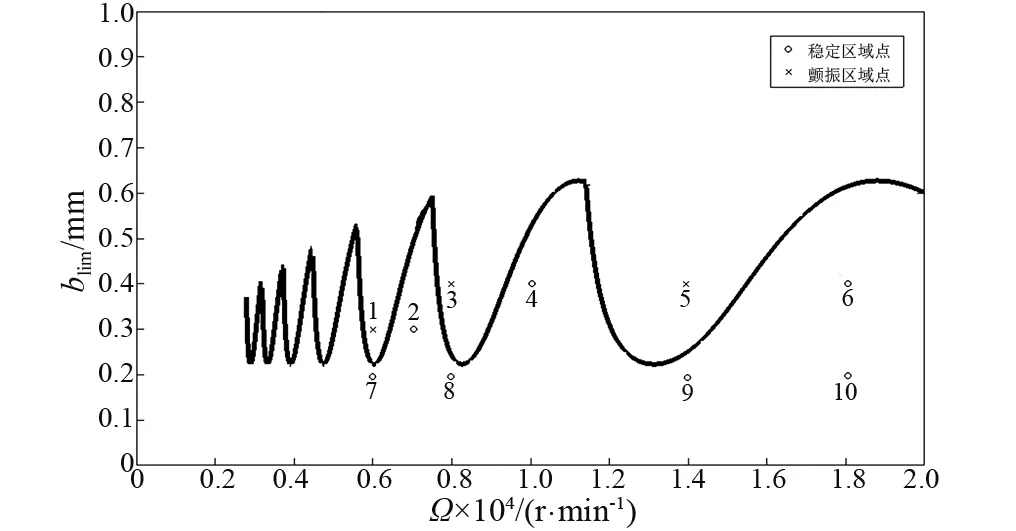
图4 未考虑陀螺效应的稳定性曲线Fig.4 Stability curves without considering gyroscopic effects

图6和图7给出考虑陀螺效应的稳定性叶瓣曲线和选取的10个点的时域响应图。分析点选取与图4位置相同的点。结果表明，1点的切削过程变成了稳定的，此点位于考虑陀螺效应和外阻的稳定性叶瓣曲线以内的区域外，即有条件稳定切削区域；2点的切削过程变成了不稳定的，此点位于考虑陀螺效应和外阻的稳定性叶瓣曲线以内的不稳定稳定切削区域；7点的切削过程是稳定的，此点位于考虑陀螺效应和外阻的稳定性叶瓣曲线以外的无条件稳定切削区域。其余点的时域响应图见图7。

图4、图5和图6、图7显示出颤振稳定性叶瓣曲线的预测结果与时间响应仿真稳定性的预测结果是一致的，说明考虑陀螺效应和外阻与不考虑陀螺效应和外阻的镗削颤振稳定性预测的正确性；另一方面，从图4和图6还可以明显看出，考虑陀螺效应和外阻与不考虑陀螺效应和外阻的镗杆稳定性叶瓣曲线的形状发生了变化，相同位置的点的切削稳定性特性也随之发生的变化。

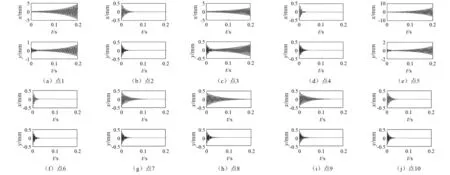
图5 未考虑陀螺效应的时域响应图Fig.5 Time domain response diagram without considering gyroscopic effect

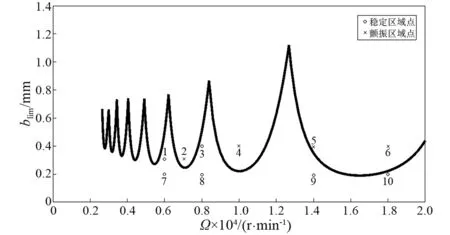
图6 考虑陀螺效应的稳定性曲线Fig.6 Stability curves with considering gyroscopic effects

在不考虑陀螺效应的情况下，本文模型得到的极限深度为0.217 mm(见图4)；在考虑陀螺效应情况下得到的极限深度为0.191 mm(图6转速16 400 r/min对应的切削深度)，而Pratt等的实验结果约为0.2 mm，与本文考虑陀螺效应的结果基本一致。

4.3 不同因素对镗削颤振稳定性的影响

为了研究不同因素对加工过程稳定性的影响，下面分别从4个方面进行分析：镗杆转动的影响；镗杆阻尼的影响；镗杆刚度的影响；切削刚度的影响。

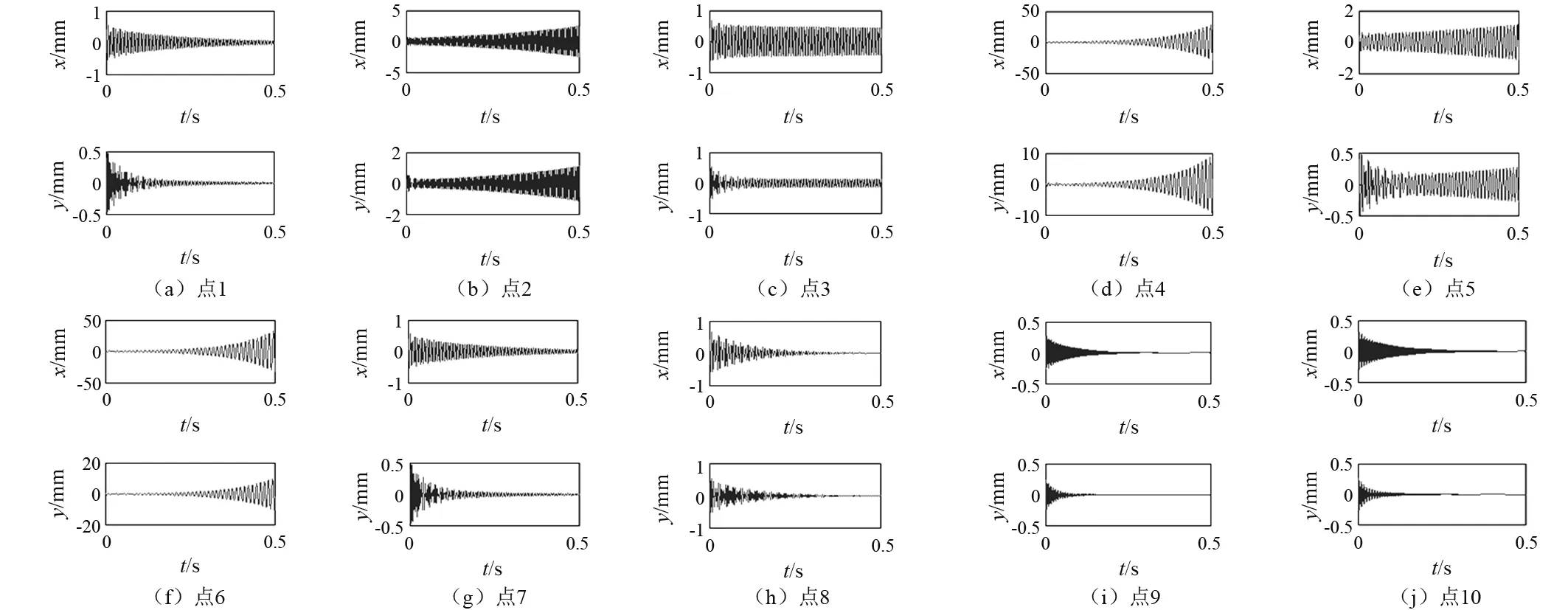
图7 虑陀螺效应的时域响应图Fig.7 Time domain response diagram with considering gyroscopic effect

4.3.1 陀螺效应的影响

如图8所示，实线所示的考虑陀螺效应的极限临界切削深度对比如虚线所示未考虑陀螺效应的极限临界切削深度，在高转速区域时的曲线向左下方发生了偏移，而且依赖随着速度的升高下降了的越多。即说明考虑陀螺效应的高速镗削颤振稳定区域变小了，陀螺效应在高速切削系统中发挥负阻尼的作用。同时发现在低转速区域的稳定性区域将扩大。因此，在镗削中陀螺效应对系统动态特性和稳定性极限的影响是不可忽略的，特别是在高速镗削领域需要考虑陀螺效应的影响。

上述关于旋转陀螺效应降低切削稳定性的分析结果，是与Mosaddegh等研究中的理论预测结果以及Li等的实验结果，在定性上是一致的。

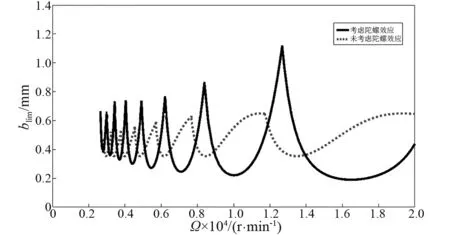
图8 陀螺效应对镗削稳定性的影响Fig.8 The influence of the gyroscope effect on the stability of boring

4.3.2 内、外阻的影响

为了比较内阻和外阻变化对颤振稳定性的影响，考虑两种情形：一是保持内阻不变，研究内阻小于、等于和大于外阻的三种情况，结果见图9；二是保持外阻不变，研究外阻大于、等于和小于内阻的三种情况，结果见图10。

由图9和10可见，内阻和外阻之和越大，则切削过程越稳定(如图9和图10中的点虚线)；在内阻和外阻之和保持不变的情况下，内阻越大，切削过程也越稳定(比较图9和图10中的实线或者点虚线相对于虚线的位置，注意在图9和图10中的虚线是相同的)。

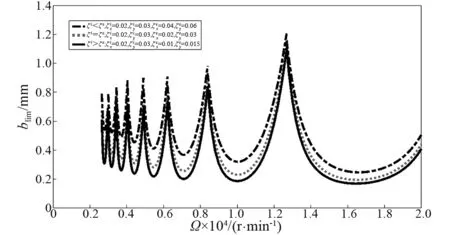
图9 内阻不变下外阻变化对镗削稳定性的影响Fig.9 The influence of external damping on the stability of boring under constant internal damping

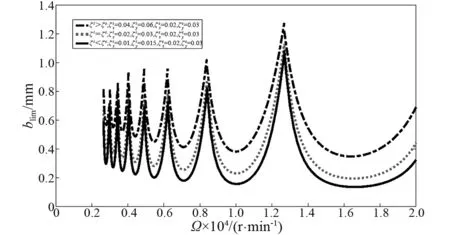
图10 外阻不变下内阻变化对镗削稳定性的影响Fig.10 Effect of internal damping on boring stability under constant external damping

图8表示内阻与外阻相等、内阻等于0并且外阻不等于0，以及外阻等于0同时内阻不等于0，三种情况下的颤振稳定性叶瓣曲线的比较结果。由图11发现，在同样的变化下，内阻对于镗削稳定性的影响大于外阻对于镗削稳定性的影响，也可以说内阻变化比外阻变化对镗削稳定性的影响更大。同时，结合图9～图11，表明在一定的转速范围内，内阻对切削颤振起着抑制的作用，这与外阻的作用是相同的，但是相比外阻而言，内阻的作用似乎要更为明显。

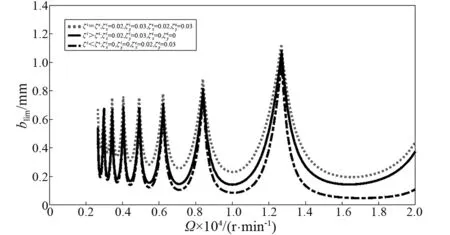
图11 内阻和外阻对镗削稳定性的影响Fig.11 The effect of internal and external damping on the stability of boring

4.3.3 镗杆刚度的影响

在保持其他的参数不发生变化的前提下，改变系统刚度，分析对其颤振稳定性的影响，得到如图12中的稳定性曲线就是在系统刚度取不同值得到的3组曲线。

图12 系统刚度对稳定性影响Fig.12 Effect of boring bar stiffness on stability

从图12中观察到系统刚度对加工系统稳定性有重要的影响，镗杆的刚度系数越大，最小极限切深越大。

4.3.4 切削刚度的影响

图13表示切削刚度对其颤振稳定性的影响，得到如图13中的稳定性曲线。从图13可以看出，随着切削刚度的变大，稳定性曲线的最小极限切深变小。因此，选择切削刚度过高的刀具，反而会降低切削过程的颤振稳定性。

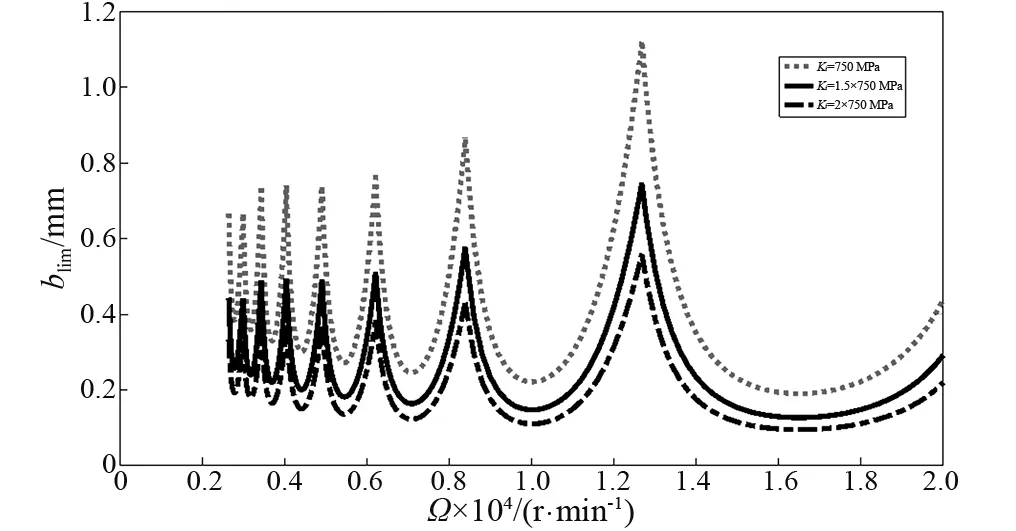
图13 系统切削刚度对稳定性影响Fig.13 Effect of cutting stiffness on stability

5 结 论

研究考虑旋转陀螺效应以及内、外阻的镗杆再生颤振稳定性。将镗杆结构简化为二自由度振动系统，采用线性再生时滞型模型对镗削力进行建模，提出了再生型镗削系统颤振稳定性极限的预测模型与求解公式。构造了根据主轴转速更新系统的固有频率和传递函数，并确定转速相关的切削稳定性边界的稳定性叶瓣图的计算方法，利用时域响应验证了稳定性曲线的正确性。并且研究了旋转陀螺效应、内外阻、镗杆弯曲刚度以及切削刚度对临界切削深度的影响。结果表明：

(1) 在旋转陀螺效应影响下，陀螺效应导致系统固有频率分叉为成正、反进动频率。

(2) 反进动频率是决定稳定边界的关键因素，稳定性曲线发生了倾斜下降。这说明陀螺效应在高速切削系统中发挥负阻尼的作用。即考虑陀螺效应的高速镗削稳定性区域减小，陀螺效应降低了镗削的临界切削深度。

(3) 内阻与外阻之和越大，切削稳定性越好。当考虑外阻因素时，在内阻与外阻之和固定的情况下，内阻对于镗削稳定性的影响大于外阻对于镗削稳定性的影响。

(4) 提高系统刚度和系统切削刚度分别增大和减小镗削颤振的稳定性区域。所以应尽量采用系统刚度大的，切削刚度小的材料设计镗杆避免颤振的发生。