折叠球形气囊展开过程仿真

梁鹏，薛齐文，张岩，刘旭东,李慧通

(1.大连交通大学 土木工程学院，大连 116028)(2.北京机械设备研究所，北京 100854)

0 引 言

气囊应用范围广泛，涉及航空航天、汽车工程等多个领域，具有广阔的应用前景和研究价值。球形气囊是气囊在应用时的一种特殊形态，其展开过程复杂，折叠过程繁琐，采用实验手段对其进行研究存在诸多不便，运用有限元数值模拟方法不仅可以减少不确定因素对实验效果的影响，还能大量节省时间和财力，解决实验手段中相对难以处理的问题[1]。

气囊模拟理论研究方面，气囊缓冲约束系统及通用气囊数学建模工具的创建，为气囊的数值模拟计算奠定了基础。在通用气囊模型基础上考虑非理想气体的影响，由此提出了控制体积法[2](CV法)。ALE法[3-5]即任意拉格朗日欧拉法，结合了拉格朗日和欧拉方法，在大变形问题处理上有较强的适用性，但求解时需要建立气体流动环境的细化网格，对计算机硬件要求较高。代小芳等[6-7]对折叠气囊展开过程的实现方法进行对比，指出了CV法和ALE法的优缺点，并细致研究了气囊建模和折叠阶段可能遇到的问题。

气囊模拟应用研究是体现气囊理论应用价值的途径。李旭波[8]对航空器着陆气垫进行探究，建立了航空器着陆的有限元模型，模拟了气垫式起落系统，完成了航空器整体着陆过程的仿真分析；喻先勇[9]对自适应压力气囊在航空零件加工中的应用进行了仿真分析，证明了自适应压力气囊可以提高航空零件的加工精度且精度可控;张九阳[10]在无人机回收方法研究中考虑了气囊的减震效果，但并没有对气囊的折叠方式进行探讨;吴军亭等[11]设计出环形气囊的一种新的折叠方法，没有针对球形气囊进行研究；卫剑征等[12]对“Z”型折叠缓冲气囊进行了仿真分析，其着眼点主要在气囊的缓冲性能，对充气速率和折叠次数对气囊展开的影响没有进行深入讨论。气囊的展开过程是气囊能否正常进行工作的关键，因为气囊在应用时通常需要被折叠进狭小空间内，在充气结束后展开到特定体积或形状，折叠和充气方式的不同会导致气囊展开效果的差异，对气囊展开效果的影响不可忽略。对于此类非线性大变形结构的动力学问题，进行模拟仿真能有效规避实体实验过程中的诸多不确定因素，可重复性高，针对性强。

鉴于目前国内外对折叠球形气囊的研究较少，本文构建单侧内折球形气囊模型，对折叠球形气囊充气展开过程动态特性进行分析。通过数值仿真模拟得到气囊在不同折叠次数、充气速率以及不同充气量情况下展开过程的计算结果，探讨上述因素对气囊展开效果的影响。

1 气囊CV展开方法

将气囊看成不断扩大的控制体积(Control Volume)，组成气囊的壳单元作为控制表面，控制表面所包围的体积即为气囊的控制体积。此方法假定：气囊内部处处等压,充气过程为准静态，气体惯性不予考虑,整个充气过程绝热。控制表面和控制体积可由格林定理相互联系：

(1)

式中：nx为表面法线与x轴夹角的余弦值，y和z方向也可类似表示。

选择任意函数φ=1，ψ=x，则体积积分可表示为

(2)

式(2)中表面积分用组成气囊的壳单元来估算：

(3)

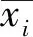
由式(3)得到气囊控制体积，内部压力由理想气体Gramm状态方程得到：

P=(k-1)ρe

(4)

式中：P为气囊内部压力；k为热容比常数，k=Cp/Cv；ρ为气体密度；e为气囊内气体比内能。

2 球形气囊模型

所建气囊模型可看作气囊未充气时折叠后水平铺展。以将半径为500 mm的球形气囊平均分为4瓣的模型为例，介绍建模方法。点坐标计算示意图如图1所示，边缘线如图2所示，网格单元如图3所示。

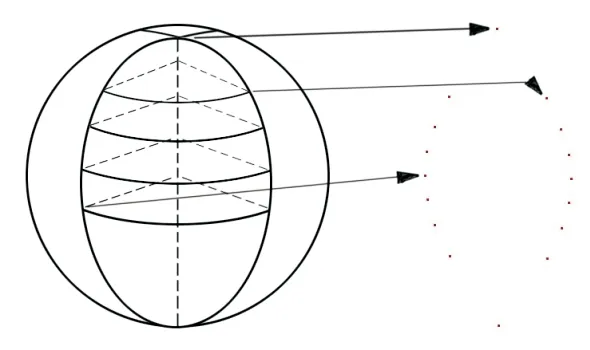
图1 点坐标计算示意图Fig.1 Schematic diagram for calculating point coordinates

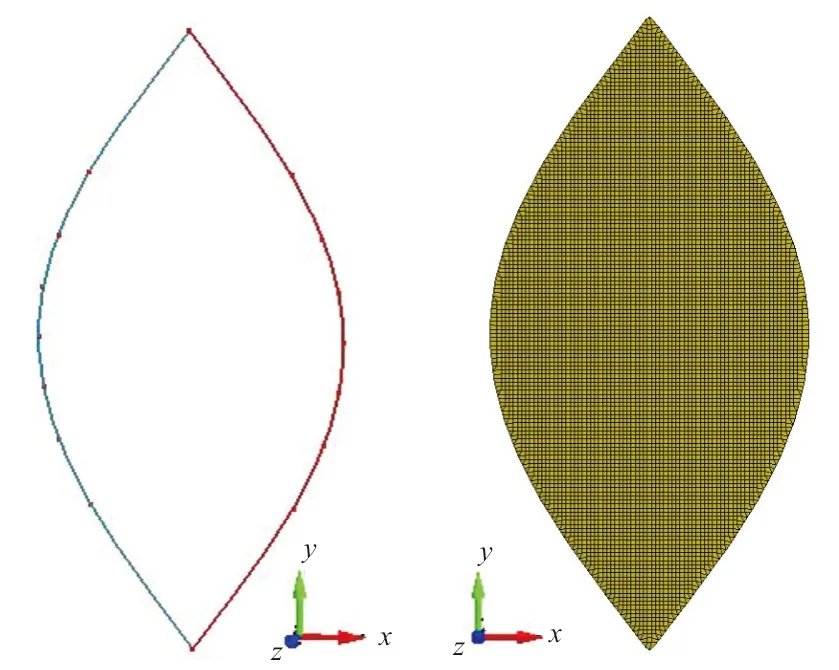
图2 边缘线 图3 网格单元
Fig.2 Edge line Fig.3 Mesh elements

根据球形气囊的半径，计算球体表面四分之一的尺寸。以500 mm为半径所建点的坐标为(0,±785.4)，(±259.8,±424.0)，(±340.1,±261.8)，(±380.23,±126.35)，(±392.7,0)，将点顺次连接成每瓣气囊的边缘线，边缘线内部划分网格，沿z方向复制网格三次，上下相邻网格间的距离为2 mm，四瓣球体表面就按顺序依次排列，如图4所示。沿y轴方向看去，效果如图5所示，按照图中的形式将气囊边界缝合。缝合方法是将需要缝合的点按图示方向移动至同一坐标位置，两点缝合为一点，使网格组成一个闭合的球体。

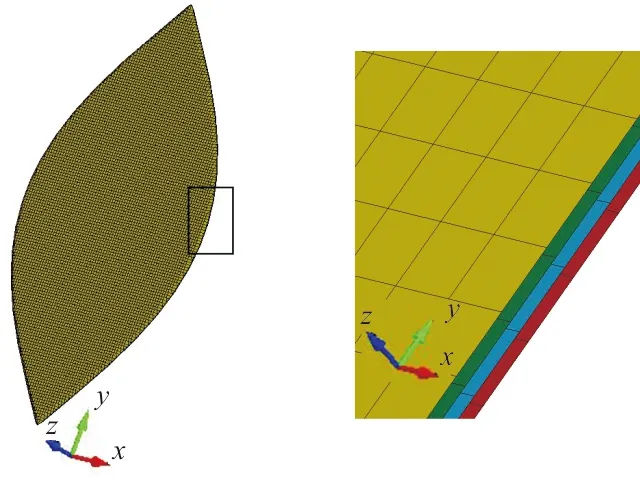
图4 单元排列Fig.4 Elements arrangement

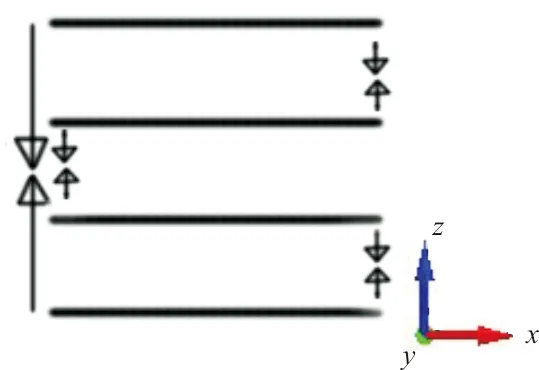
(a)整体示意图

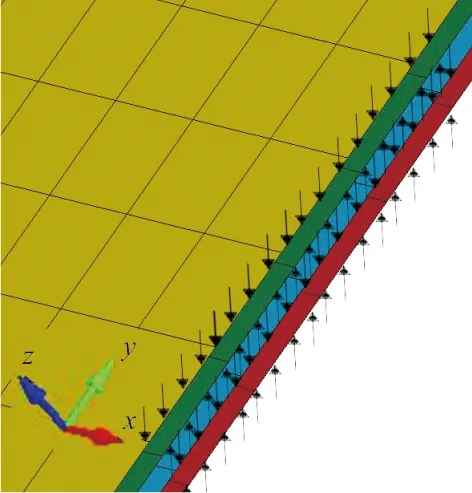
(b)局部示意图图5 气囊缝合方式Fig.5 Way of merging airbag

采用同样的方法，建立4组模型进行对比，分别是将气囊表面分成4瓣、6瓣、8瓣、10瓣。相当于将球形气囊模型按单面内折的方法分别折叠了1、2、3、4次。建模完成后的折叠气囊模型侧面效果图及展开效果图如图6所示。

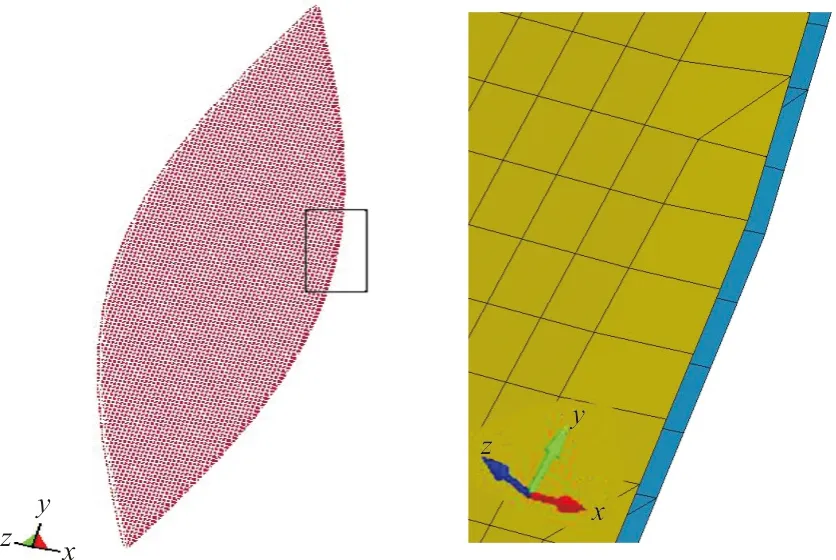
(a)放大区域 (b)折叠1次气囊边缘

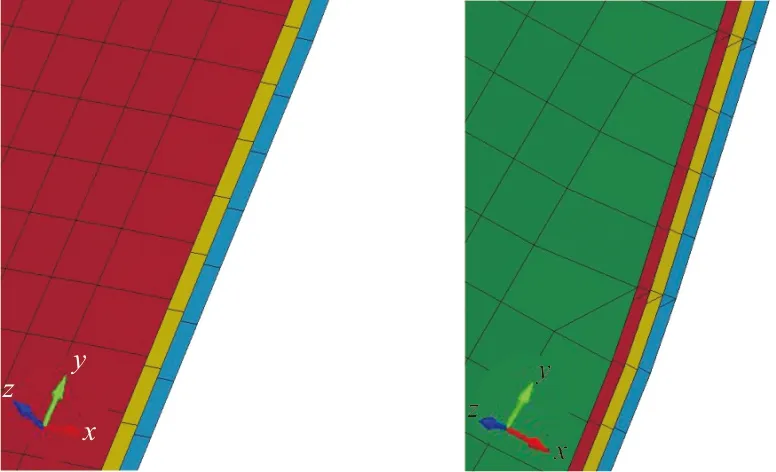
(c)折叠2次气囊边缘 (d)折叠3次气囊边缘

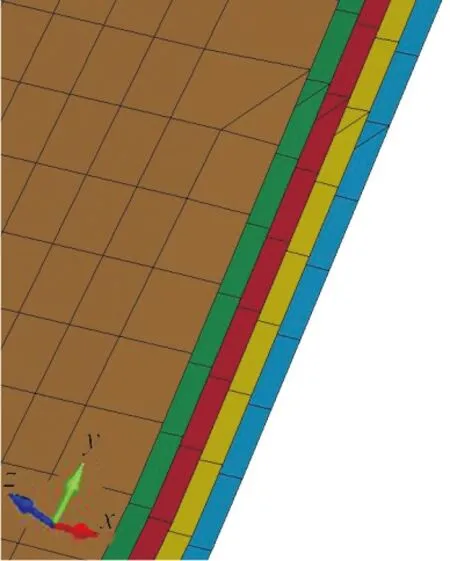
(e)折叠4次气囊边缘

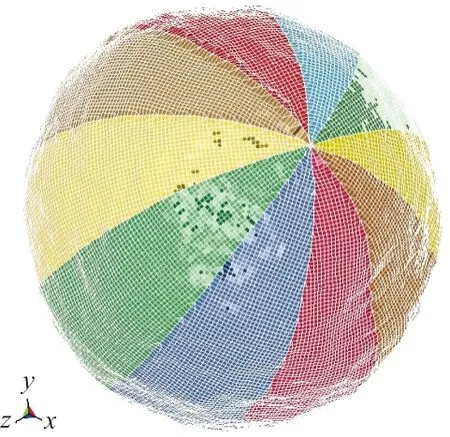
(f)折叠4次气囊展开图图6 单侧折叠/展开气囊模型Fig.6 Folded airbag model

此方法直接构建单侧内折后的球形气囊模型，可以省去对气囊进行二次折叠。气囊二次折叠会使折叠区域单元变形，折叠次数越多，整体变形量越大，导致气囊展开后数据产生误差，此方法可以有效避免因折叠变形带来的误差。

3 数值模型计算

针对同一种材料的球形气囊进行探究，就气囊折叠层数、充气速率和充气量的不同对气囊内压和体积的影响进行对比分析。计算时所设定的大气温度为98 K，大气压强为0.101 MPa，大气密度为1.29 g/L。气囊相关参数如下：单元类型为薄膜单元，质量密度870 kg/m3，弹性模量500 MPa，泊松比0.3，厚度0.38 mm，球体展开后半径500 mm，划分的网格边长为10 mm，每层之间的距离为2 mm。

3.1 折叠次数

不同折叠次数下，充气速率与时间曲线统一为加载曲线，如图7所示。图中，曲线中有标识“A”处为转折点，转折点坐标分别为(0,0)，(1,0.5)，(3,0.93)，(3,0)，其物理含义表示0～1 s内，充气速率从0均匀增加到0.5 g/s，1～3 s内，充气速率由0.5均匀增加到0.93 g/s，3 s后停止充气。整个充气过程中气囊完全自由展开。

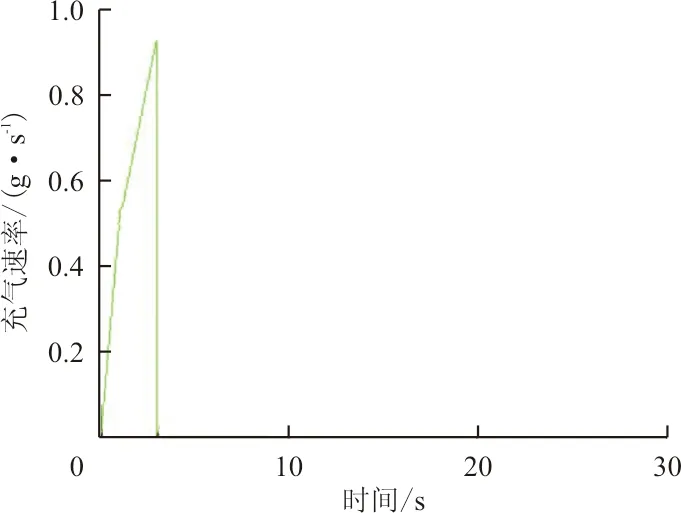
图7 加载曲线Fig.7 Load curve

球形气囊体积和内压变化曲线如图8～图9所示。

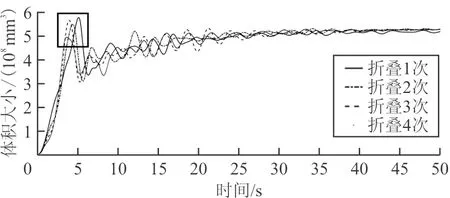
(a)曲线整体

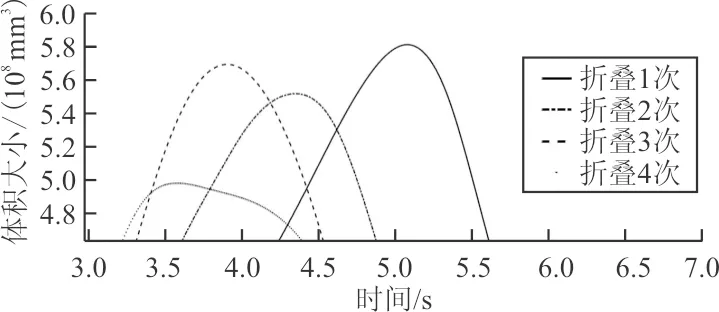
(b)局部放大图8 气囊体积与时间关系曲线Fig.8 Airbag volume and time relation curve

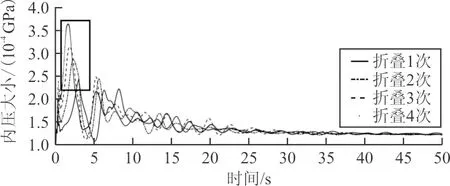
(a)曲线整体

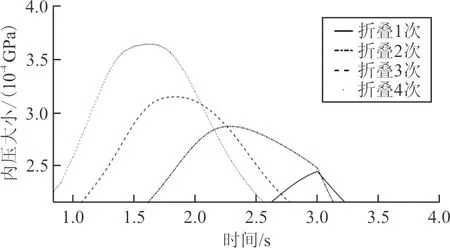
(b)局部放大图9 气囊内压与时间关系曲线Fig.9 Airbag internal pressure and time relation curve

从图8～图9可以看出：随着折叠次数的增加，球形气囊首次达到体积极大值的时间提前，首次达到内压最大值的时间亦提前，而且内压最大值增大。由此可以推断，充气条件相同时，单侧内折折叠次数与内压最大值成正相关。

3.2 充气速率

在充气量相同的情况下，针对同一模型，给出充气速率不同时，气囊内部体积和压力随时间变化的曲线。各加载情况下充气速率与时间的关系如图10所示。

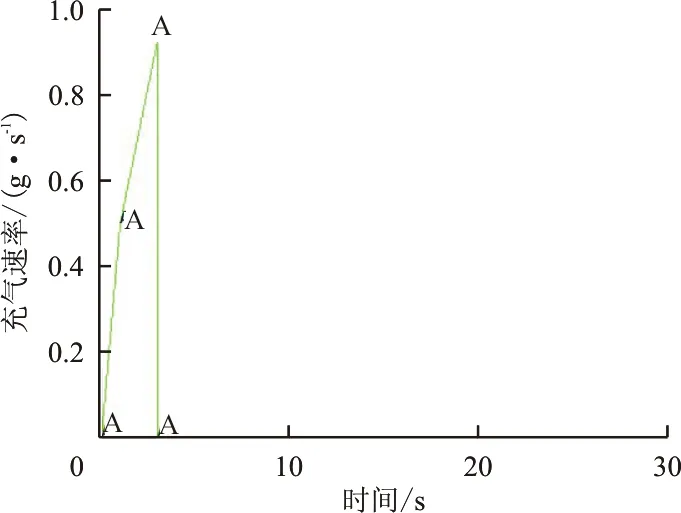
(a)加载曲线1

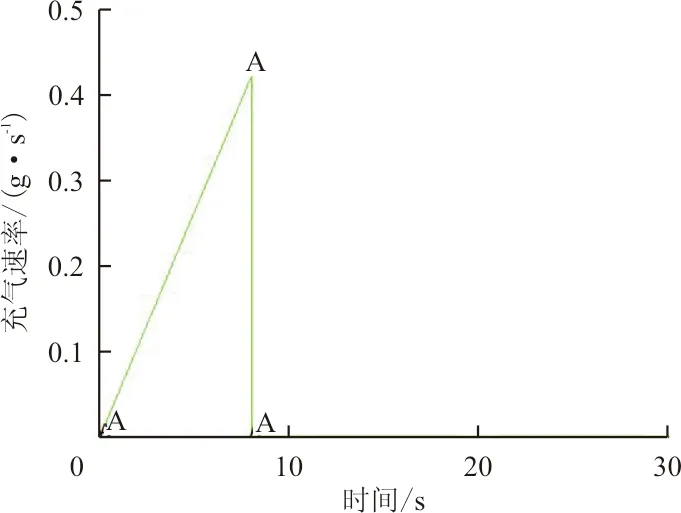
(b)加载曲线2

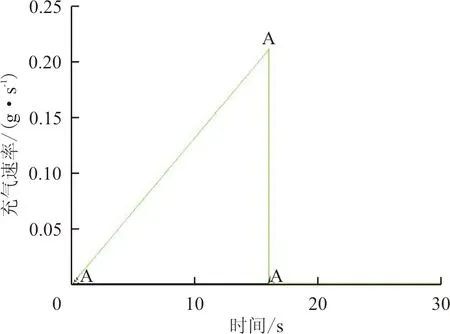
(c)加载曲线3图10 加载曲线Fig.10 Load curve

从图10可以看出：曲线1与图7的加载曲线相同，图中加载曲线与横坐标轴所围成的面积便是充气总量，三种加载情况充气总量相同；曲线2表示在0～8 s内，充气速率从0均匀增加至0.42 g/s后停止充气；曲线3表示在0～16 s内，充气速率从0均匀增加至0.21 g/s后停止充气。

球形气囊对应的体积和内部压力随时间的变化曲线如图11～图12所示。

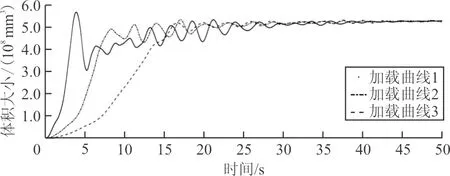
图11 气囊体积与时间关系曲线Fig.11 Airbag volume and time relation curve

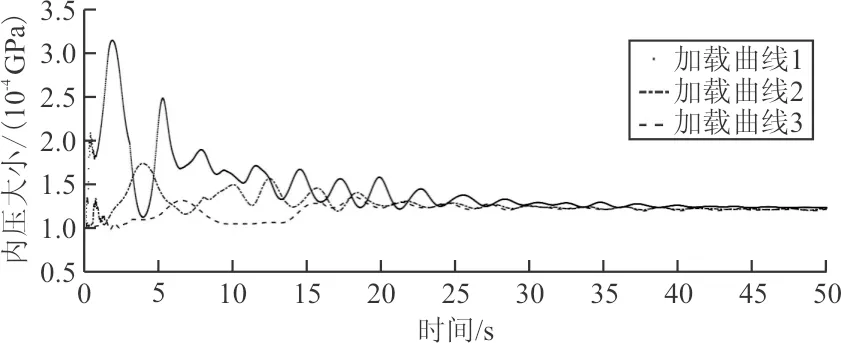
图12 气囊内压与时间关系曲线Fig.12 Airbag internal pressure and time relation curve

从图11～图12可以看出：在充气速率较快的情况下，体积与内压曲线变化幅度更大，全部气体充入气囊后，需要更长的时间才能稳定；气囊内压会更快到达峰值，而且峰值和充气速率成正相关。充气速率稍慢的情况下，气囊变化曲线较平缓，虽延长了充气时间但气囊体积和内压曲线波动明显减小。

3.3 充气量

针对同一模型，通过延长充气时间来保证充气量增大，加载曲线如图13所示。

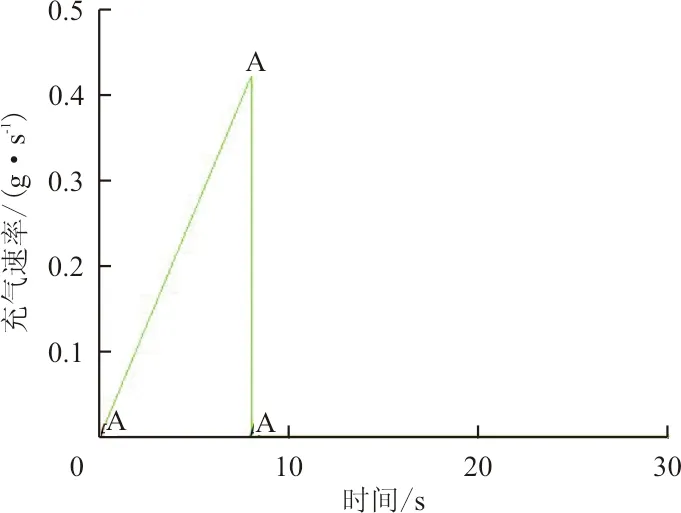
(a)加载曲线1

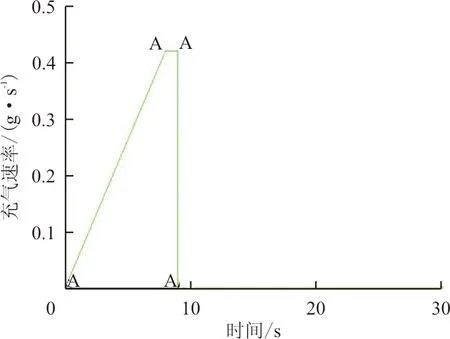
(b)加载曲线2

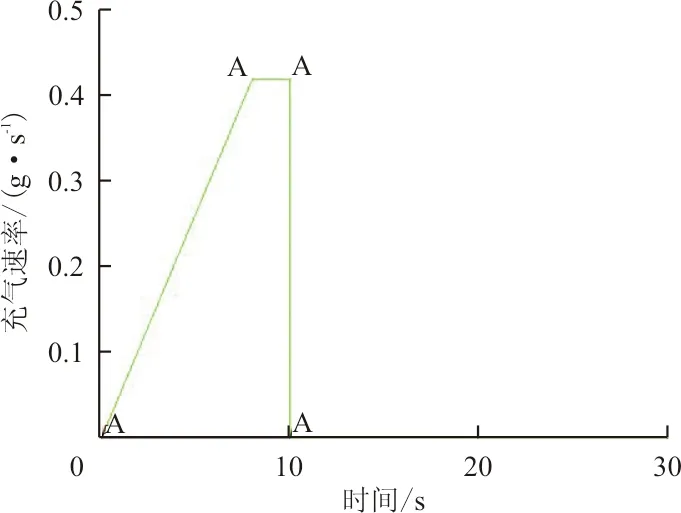
(c)加载曲线3图13 加载曲线Fig.13 Load curve

从图13可以看出：三种加载情形中，前8 s加载情况相同，充气速率由0均匀增加至0.42 g/s；曲线1在8 s后停止充气，曲线2在8 s后按0.42 g/s的速率充气至9 s，曲线3充气至10 s，由此区分充气量大小。

球形气囊对应的体积和内部压力随时间的变化曲线如图14～图15所示。

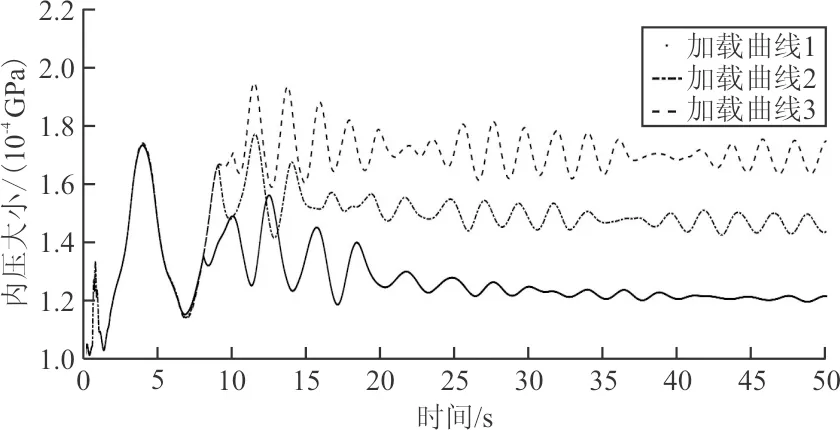
图14 气囊内压与时间关系曲线Fig.14 Airbag internal pressure and time relation curve

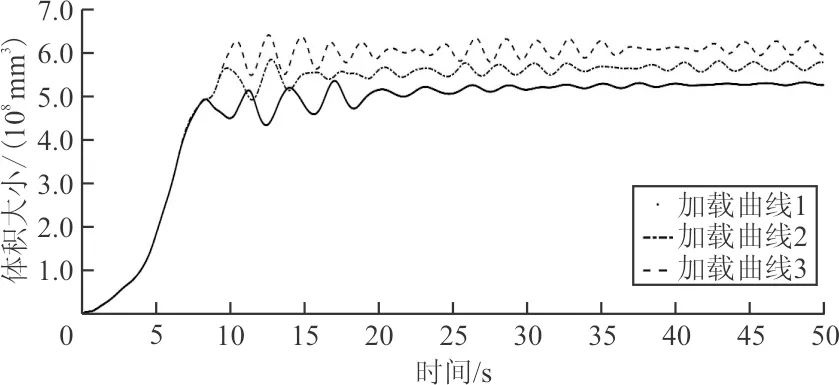
图15 气囊体积与时间关系曲线Fig.15 Airbag volume and time relation curve

从图14～图15可以看出：就该模型而言，0～8 s充气过程中各曲线没有明显差别，差别出现在8～10 s之间，持续加载阶段，随着充气量的增加，曲线波动愈发明显，难以稳定到固定数值。

为了更清晰地表示出不同充气量时气囊平衡阶段体积与内压的关系，以气囊展开30～50 s时间段内的平均值作为平衡数据，计算三种加载情况下气囊体积与内压的相对大小，如表1所示。

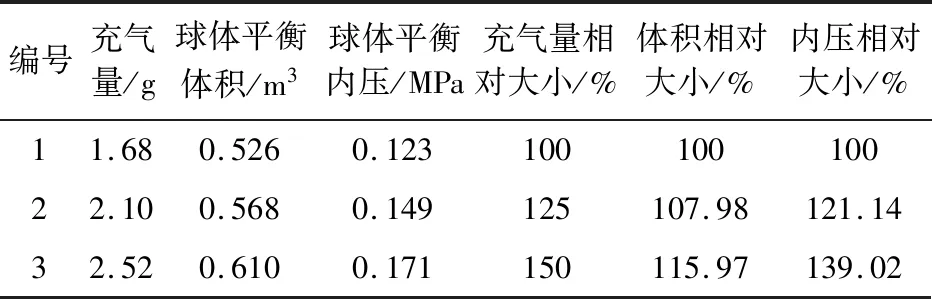
表1 计算结果比例关系Table 1 Proportional relation of results

从表1可以看出：以加载情况1作为参考，当充气量增加25%时，体积增大7.98%，内压增大21.14%；当充气量增加50%时，体积增大15.97%，内压增大39.02%。

4 结 论

(1)对于单侧内折方式折叠的球形气囊，随着折叠次数的增多，气囊首次展开到体积极大值的时间缩短，层与层之间相互作用增多，充气初始阶段的内压最大值增大。若对气囊应用此折叠方法，应注意折叠次数对内压最大值的影响，避免折叠次数过多使内压最大值超过气囊材料承受极限而造成破坏。

(2)在保证气囊材料不被破坏的前提下，充气速率和充气量对气囊产生的影响主要在稳定性方面，但两者对稳定性的影响产生在不同阶段。充气速率的影响产生在气囊充气和初期展开阶段，充气量的影响产生在充气完成后的自由展开阶段。充气量相同的情况下，充气速率越高，气囊展开初期的内压和体积曲线波动越明显，而且内压最大值显著升高；充气速率相同，充气量越高，充气完成后气囊体积和内压曲线的波动幅度越大。