混凝土框架子结构角柱快速移除数值分析

周云 胡翔 陈太平 易伟建

摘   要：研究了钢筋混凝土（RC）框架子结构在角柱突然失效模式下剩余结构的动力响应.依据Qian等完成的角柱快速移除动力试验，利用大型有限元软件ABAQUS/Explicit建立了精细化的有限元模型.在有限元模型中考虑了钢筋混凝土材料的应变率效应，并进行了现场试验的全过程加载模拟，模拟获得的位移响应曲线和破坏模式与现场试验吻合良好，较好地模拟了混凝土框架子结构角柱快速移除试验的全过程.在成功进行了模型校验的基础上，分析了角柱的失效时间和横向水平约束刚度对结构动力响应的影响，结果表明，延长结构的失效时间和增大横向水平约束刚度均能够有效地提高结构的抗倒塌性能.

关键词：钢筋混凝土结构;连续倒塌;快速移除;ABAQUS/Explicit

中图分类号：TU375.4                              文献标志码：A

Abstract： The dynamic response of the remaining structures under sudden failure of a corner column in a reinforced concrete （RC） frame structure was studied. The finite element model of ABAQUS / Explicit was established based on the loss of a corner column tested by Qian K. The finite element model took into account the strain rate effect of reinforced concrete materials and simulated the actual loading process. The simulation results were in good agreement with the field-test dynamic response curves and failure modes， which simulated the whole process of sudden removal of a corner column. Based on the finite element model， the influence of corner column failure time and lateral restraint stiffness on the dynamic response of the structure was analyzed. The results show that prolonging the failure time and increasing the lateral horizontal restraint stiffness can effectively improve the collapse resistance of the structure.

Key words： reinforced concrete;progressive collapse;sudden removal;ABAQUS/Explicit

早期英國伦敦的Roman Point公寓倒塌事故引发了人们对结构连续倒塌的关注，结构抗连续倒塌本质上属于复杂的动力非线性过程[1].针对混凝土框架结构连续倒塌问题，相关学者开展了大量的试验研究，但集中在混凝土子结构层次，着重研究结构倒塌受力机理的动力连续倒塌试验研究不多：2011年，Tian等[2]进行了4个1/2缩尺的混凝土框架子结构中柱的快速移除试验，研究了构件在不同级别荷载作用下的动力响应.2012年，Qian等[3]进行了6个1/3缩尺的混凝土框架子结构的角柱快速移除试验，研究了跨长、抗震措施等因素对结构承载力的影响. 2013年，高超、宗周红等[4]进行了3层钢筋混凝土框架结构模型在不同炸点位置、距离、当量等条件下的爆炸荷载试验.2014年，Orton等[5]完成了一榀两层两跨的平面框架子结构的中柱快速移除试验，动力试验中观察到悬链线效应可提高结构承载能力. 2013年，李凤武等[6]完成了1/2比例的3层3跨钢筋混凝土空间框架的倒塌试验，试验结果表明，材料在瞬时荷载作用下强度的提高有利于减小动力效应对结构的影响.2014年，Yu等[7]对一个梁柱混凝土框架子结构的中柱进行了爆炸移除试验，试验表明结构在动力响应下，钢筋的应变率可达10-2～10-1/s. 2015年，何庆锋等[8]完成了两榀两跨单层平面框架的静动载试验，研究了试件的位移、加速度和钢筋应变等动力响应数据.

结构动力抗连续倒塌试验对场地条件、设备要求较高，因此一般的动力试验的构件数目较少，相关参数的对照试验组也较少. 为深入研究结构在动力荷载作用下的受力机制、破坏模式和参数影响等，精细化的有限元研究是必要的.关于混凝土框架结构连续倒塌数值模拟方面，已开展的研究工作有：2008年，Sasani等[9]根据一个3/8缩尺的混凝土框架子结构的中柱移除试验建立了有限元模型，研究了移除各层柱之后的模型动力响应.2013年，高超、宗周红等[4]结合试验建立了角柱爆炸荷载作用下钢筋混凝土有限元模型，模型结果基本反映了实际试验过程中的动力响应.2014年，李凤武等[10]对已完成的1/2缩尺的3层3跨钢筋混凝土空间框架的倒塌试验，利用SAP2000建立了线性有限元模型，分析结果与试验吻合较好. 2016年，Pham等[11]根据完成的爆炸荷载快速移除试验建立了有限元模型，研究表明水平方向约束对结构防倒塌性能有至关重要的作用.2016年，何庆锋等[12]利用有限元软件AUTO-DYN研究了钢筋混凝土框架结构在爆炸移除柱之后的结构动力响应和破坏形态，该模型考虑了材料应变率的影响.

上述研究发现，在动力响应作用下混凝土和钢筋等材料的应变率可达到一个较高水平[6-8]，而混凝土和钢筋等材料属于应变率敏感材料，即材料力学属性在不同应变率下有较大幅度的改变，材料在高应变率下的增益对防止结构的连续倒塌有较大贡献[6]，因此在结构动力连续倒塌研究中考虑材料应变率效应是十分必要的. 本文拟选取Qian等[3]在2012年完成的混凝土框架子结构角柱快速移除试验作为有限元模拟的原型试验. 相对于其他学者的试验，该试验着重研究了混凝土框架子结构在动力荷载作用下的受力机理和失效模式，是理想的精细化有限元模拟原型试验. 本文根据该试验提供的试件信息和试验结果，利用大型有限元软件ABAQUS/Explicit建立了精细化有限元模型，结合钢筋混凝土材料的应变率效应，较好地模拟了现场试验的加载全过程，模型结果与现场试验结果吻合良好. 在成功进行模型校核的基础上，分析了角柱失效时间和横向水平约束刚度对结构抗连续倒塌性能的影响.

1   Qian等角柱快速移除试验简介

Qian等[3]进行了6个1/3缩尺的混凝土框架子结构角柱快速移除动力试验. 试件为包含角柱节点的子结构，试件外观和现场加载方案如图1所示. 试件设计按照新加坡CP65标准，抗震设计按照美国ACI319—08规范，抗连续倒塌的荷载组合按照美国DOD规范选取，见表1.该试验共设计了DF1～DF6等6个工况，各试件由于不同的原因导致了部分数据的缺失，本文选取其中的DF1和DF2试件进行数值分析，试件通过快速移除装置进行角柱轴力的快速释放，DF1和DF2的角柱轴力释放过程如图2所示，释放时长大约在0.003 0～0.003 5 s. 所选试件基本尺寸和配筋布置如图3和表1所示，混凝土和钢筋的材料属性如表2所示.

2   有限元建模方法

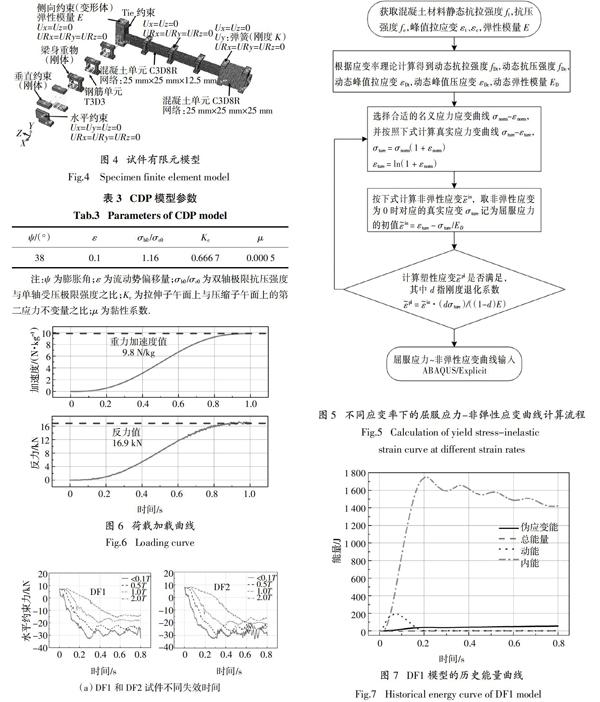
本文根据试验数据建立了2个和试件相同尺寸和边界条件的有限元模型，如图4所示. 混凝土采用八节点的减缩积分实体单元C3D8R，钢筋采用两节点桁架单元T3D2，采用ABAQUS自带的嵌入单元来模拟钢筋和混凝土之间的锚固关系，不考虑二者之间的滑移. 试件的边柱支座、梁身施加的重物以及角柱头侧向约束铁块均采用八节点的减缩积分实体单元C3D8R. 由于试验过程中，没有观察到边柱支座和梁身加载重物的变形，因此将两者设置成刚体以节约计算成本.试验过程中角柱头的侧向约束装置采用变形体来描述，变形体的下表面与角柱上表面采用tie连接方式. 支座与梁身加载重物和混凝土的相互作用采用ABAQUS/Explicit中的通用接触，法向采用硬接触保证双方不能发生嵌入和穿透现象，切向方向采用罚函数来模拟混凝土与钢部件之间的摩擦，摩擦因数取0.4[13]. 为了简化试验模型，梁身的重物采用等效质量的钢部件模拟，钢部件的密度值等于梁身重物除以模型钢部件体积，DF1模型中部件密度为1.34×105  kg/m3.

2.1   混凝土模型

模型中的混凝土采用ABAQUS中的CDP （concrete damaged plasticity）材料模型，该模型可模拟混凝土在低静水压力时，受到单调、循环或动载作用下的力学行为[14]，材料的屈服面和塑性流动法则参数可按表3选取[13]，还能考虑材料在不同应变率的力学行为，但需要提供材料不同应变率下的屈服应力-非弹性应变曲线和损伤因子，然后在曲线中插值取用. 本文的混凝土单轴受拉受压本构模型按照《混凝土设计规范》[15]计算，选择试验实测的混凝土抗压强度作为混凝土强度代表值，采用欧洲规范CEB-Fip model code 2010[16]中的回归公式计算混凝土材料的应变率.获取混凝土在不同应变率下的屈服应力-非弹性应变曲线按照图5步骤进行. 由于CDP模型自身的局限性，本文暂不考虑应变率对损伤因子的影响.

2.2   钢筋本构模型

钢筋采用ABAQUS自带的等向弹塑性模型，并考虑应变率的影响.钢筋单轴应力-应变曲线采用三折线线性强化模型，考虑钢筋屈服之后的强化段和下降段. 弹性模量、屈服应力均按实际测试结果选取，泊松比取值0.3.由于试验材料属性没有提供钢筋的极限应变数据，采用伸长率等效[15]，为了满足Explicit求解器数据规则化的要求，取极限应变的1%作为断裂应变与极限应变之差.本文采用应用较为广泛的Malvar提出的指数型回归公式[17]计算钢筋的应变率效应.

2.3   加载过程

现场试验加载过程分成两步，第一步在梁身缓慢地施加重物，使角柱中的竖向轴力达到预期设计值，模拟结构未失效之前受力状态;第二步待重物荷载加载完毕，角柱竖向轴力达到预期值，通过角柱下面的快速释放装置将角柱内的轴力迅速释放，模拟结构柱在受到极端荷载时的突然破坏.根据试验结果快速释放机制并不能在瞬时将角柱内的轴力完全释放，而是在一个时间范围内，释放时长大约在0.003 0～0.003 5 s[3].为了在ABAQUS/Explicit中准确模拟该加载过程，模型加载过程按如下步骤进行：

1）在角柱下表面添加一个竖向约束，缓慢施加重力场，取光滑的加载幅值曲线，并尽可能延长加载时间以减小荷载冲击的影响来模拟静力加载，并获取約束的竖向反力.图6所示为DF1试件模型重力场赋值曲线和竖向约束反力曲线，重力场取9.781 N/kg，加载时间为1 s（约为结构自振周期的6倍）. 从图6中可看出约束反力整体都较为稳定，可模拟结构重物的静力加载过程，后期微小扰动是由于梁端有微小开裂，内能释放的缘故.

2）移除第一步中角柱底面的竖向约束，将得到的角柱约束反力反向施加到角柱底面，并同时施加第一步中的重力场，以此来等效第一步中的静力加载过程. 若该过程中出现较大的动能变化，则说明第一步中提取的约束反力时间间隔过大，需要减小时间间隔重新提取约束反力值，直到模型整体的动能变化处于可接受范围之内.

3）待重力场施加完毕并保持不变，将施加在角柱底面的约束反力在试验记录的释放时长内迅速减小到零，以此模拟试验过程中的快速释放过程.

采用上述过程的意义在于ABAQUS软件中约束只能瞬时移除，不能模拟试验中在有限时长内释放内力的过程，但是力荷载能够按照一定的时间-幅值曲线释放，模拟内力释放过程，同时也为后文对结构失效时间的讨论提供前提.

3   试验与模拟结果比较

3.1   数值稳定分析

能量平衡是评估数值分析是否得到了合理可靠的响应的重要参考依据[18].总能量是指全过程中能量的总和，包括内能、黏性耗散能、动能、外力功等，在数值模型中近似一个常数. 内能包括可恢复的弹性应变能，非弹性过程中的能量耗散、伪应变能等. 伪应变能包括储存在沙漏阻力以及在壳和梁单元的横向剪切中的能量，出现大量的伪应变能则表明必须对网格进行细化或进行其他修改. ABAQUS/Explicit有2个能量限制准则来保证数值结果的有效性：1）总能量在计算过程中幅值扰动不超过均值的1%;2）伪应变能占总内能比例不超过5%.图7所示为试件DF1模型的历史能量曲线，总能量和伪应变能占比均能满足限制准则要求，最大的伪应变能占比为4.1%，说明模型网格划分可以提供一个合理的数值结果.

3.2   试验结果与模拟结果对比

DF1和DF2试件现场试验与数值模拟的角柱竖向位移响应曲线对比如图8所示.从图8中可看出模拟曲线与试验曲线吻合良好，变化趋势相同. 对于DF1试件，试验值与模拟值基本重合，位移峰值误差为1.9%，平均周期误差为5.6%.对于DF2试件，位移响应曲线后期振动段吻合较好，峰值误差为1.5%，平均周期误差为4.5%. 前期位移响应下降段吻合较差，可能的原因是实际过程中的内力释放曲线与模拟过程中采用的线性曲线不同，初期释放较慢，后期迅速加快，因此与采用线性释放曲线的模拟位移曲线相比，位移有滞后的现象，等完全释放完毕，角柱达到最低点，试验与模拟曲线有相近的位移值.图9所示为现场试验破坏模式与模型受拉损伤对比图. ABAQUS塑性损伤模型受拉损伤反映的是材料在受拉过程中刚度的折损，虽然不能直接代表结构裂缝的产生和发展，但是能够在一定程度上反映结构破坏的位置和程度. 从图9中可看出，现场试验和模拟结果显示边柱端梁上部，中柱端梁下部，以及中柱后侧混凝土均受到不同程度的受拉破坏，试验与模型吻合良好.

4   参数分析

在成功地对精细化有限元模型校核准确的基础上，本文进一步地分析了角柱的失效时间和横向水平约束刚度2个参数对结构动力响应的影响.

4.1   失效时间对结构动力响应的影响

根据美国DOD规范要求，角柱的失效时间需要小于失效后剩余结构自振周期的1/10. Qian等现场试验中DF1和DF2试件剩余结构的自振周期分别为0.156 s和0.161 s，失效时间分别为0.003 5 s和0.003 0 s，满足规范要求. 为了研究失效时间对结构动力响应的影响，分别采用试件实际失效时间和剩余结构平均自振周期的0.5倍、1.0倍、2.0倍4种工况进行对比分析.

4.1.1   角柱位移响应曲线

不同失效时间下角柱位移响应如图10（a）所示. 从图10（a）中可看出，失效时间的增大对结构的自振周期影响较小，但很大程度上削弱了结构的动力效应，峰值位移也随失效时间的增大而减小.当采用2.0倍自振周期作为试件失效时间时，相对于现场试验位移曲线，试件DF1和DF2峰值位移分别减小了37.3%和38.0%.当失效时间超过1.0倍自振周期时，位移响应曲线趋势发生了明显的改变.

4.1.2   横向水平约束反力响应

不同失效时间下边柱水平约束反力响应曲线如图11（a）所示.从图11（a）中可看出，与位移响应曲线相同，随着失效时间的增加，曲线的波动趋势越发平缓，动力效应随之减弱.当采用2.0倍自振周期作为试件失效时间时，相对于现场试验水平约束反力峰值分别减小了53.3%和41.3%.同时，所有工况中水平约束力均由最初始时的正值（受拉）转变为最终的负值（受压），说明中柱移除后试件的传力路径发生了明显的改变，并且整个过程中均未产生悬链线效应，这与Qian等在现场试验中得出的结论一致.

4.1.3    损伤对比

DF1和DF2试件在不同失效时间下结构损伤对比如图12所示.从图12中可看出随着失效时间的增加，试件DF1和DF2的损伤范围和损伤程度都有较大程度减小.

4.2   横向水平约束刚度对结构动力响应的影响

框架结构的受力性能与其周围构件的约束情况密切相关，尤其是在结构角柱失效情况下，荷载传递路径依赖于周围构件的完整性.不同大小的横向水平约束刚度反映了周边构件的约束强度.为了研究周边约束强度对结构动力响应的影响，分别采用原模型横向水平约束刚度的1.0倍（14 kN/mm）、2.0倍（28 kN/mm）、10.0倍（140 kN/mm）和剛结4种工况进行对比分析.

4.2.1   角柱位移效应曲线

不同横向水平约束刚度下的位移响应曲线如图10（b）所示.从图10（b）中可看出，水平约束刚度的增大对结构的动力效应影响较小，但对峰值位移和自振周期影响较大.当采用无穷大刚度时，相对于原模拟试验曲线采用的14 kN/mm刚度，DF1和DF2试件的峰值位移分别减小了69.6%和71.7%，自振周期分别减小了29.8%和31.1%.因此，现场试验过程中对于角柱侧向支撑刚度的监测十分重要.

4.2.2   横向水平约束反力响应

不同横向水平约束刚度下的水平约束力如图11（b）所示.从图11（b）中可看出，与位移响应曲线相反，随着水平刚度的增大，水平约束反力逐渐增大. 当采用无穷大刚度时，水平约束反力的峰值分别增大了51.9%和67.8%. 同样，与失效时间中讨论的一致，所有工况中水平约束力均由最初始时的正值（受拉）转变为最终的负值（受压），说明整个过程中均未产生悬链线效应.

4.2.3   损伤对比

DF1和DF2试件在不同水平约束刚度下结构损伤对比如图13所示.从图13中可看出随着约束刚度的增加，试件DF1和DF2的损伤范围和损伤程度都有较大程度减小.因此在实际工程中，提高失效构件的水平约束刚度，对结构防倒塌性能有显著意义.

5   结   论

本文利用大型有限元软件ABAQUS，对Qian K等框架子结构角柱快速移除动力试验进行了精细化的有限元模拟. 在此基础上，研究了角柱失效时间以及横向水平约束刚度对结构动力响应的影响. 本文的主要结论如下：

1）结合应变率理论的精细化有限元模型和Qian等框架现场试验结果吻合良好，说明ABAQUS塑性损伤材料模型能够很好地考虑混凝土在不同应变率下的受力性能，采用《规范》推荐的混凝土本构是可行的.

2）失效时间的增大在很大程度上削弱了结构的动力效应，当采用2.0倍自振周期作为失效时间时，相对于现场试验数据，试件DF1和DF2的峰值位移分别下降了37.3%和38.0%，水平约束反力峰值分别减小了53.3%和41.3%，损伤范围和损伤程度都有较大程度减小.

3）角柱的横向水平约束刚度对试件的动力响应影响较大，当采用无穷刚度的水平约束时，相对于现场试验数据，试件DF1和DF2的峰值位移分别下降了69.6%和71.7%，自振周期分别减小了29.8%和31.1%，水平约束反力的峰值分别增大了51.9%和67.8%，损伤范围和损伤程度都有较大程度减小.

参考文献

[1]   陆新征，李易，叶列平.混凝土结构防连续倒塌理论与设计方法研究[M].北京：中国建筑工业出版社，2011：1—30.

LU X Z，LI Y，YE L P.Study on the theory and design method of preventing continuous collapse of concrete structures[M].Beijing：China Architecture & Building Press，2011：1—30.（In Chinese）

[2]    TIAN Y，SU Y.Dynamic response of reinforced concrete beams following instantaneous removal of a bearing column[J].International Journal of Concrete Structures and Materials，2011，5（1）：19—28.

[3]  QIAN K，LI B.Dynamic performance of RC beam-column substructures under the scenario of the loss of a corner column—Experimental results[J]. Engineering Structures，2012，42：154—167.

[4]   高超，宗周红，伍俊. 爆炸荷载下钢筋混凝土框架结构倒塌破坏试验研究[J]. 土木工程学报，2013，46（7）：9—20.

GAO C，ZONG Z H，WU J.Experimental study on progressive collapse failure of RC frame structures under blast loading[J].China Civil Engineering Journal，2013，46（7）：9—20.（In Chinese）

[5]  ORTON S L，KIRBY J E. Dynamic response of a RC frame under column removal[J]. Journal of Performance of Constructed Facilities，2013，28（4）：1—8.

[6]   李鳳武，肖岩，赵禹斌，等.钢筋混凝土框架中柱突然失效模拟试验[J].建筑结构，2013，43（23）：57—61.

LI F W，XIAO Y，ZHAO Y B，et al.Collapse tests of RC frame with sudden middle column removal[J]. Building Structure，2013，43（23）：57—61.（In Chinese）

[7]   YU J，RINDER T，STOLZ A，et al.Dynamic progressive collapse of an RC assemblage induced by contact detonation[J]. Journal of Structural Engineering，2014，140（6）：1—13.

[8]   何庆锋，刘义仁，蒋曲，等.锤击作用下钢筋混凝土框架倒塌性能试验研究[J].湖南大学学报（自然科学版），2015，42（1）：40—46.

HE Q F，LIU Y R，JIANG Q C，et al.Experimental study of the collapse performance of RC frame under hammer load[J]. Journal of Human University（Natural Sciences），2015，42（1）：40—46.（In Chinese）

[9]   SASANI M，KROPELNICKI J.Progressive collapse analysis of an RC structure[J]. The Structural Design of Tall and Special Buildings，2008，17（4）：757—771.

[10]  李鳳武，肖岩，赵禹斌.钢筋混凝土框架边柱突然失效模拟试验与分析研究[J].土木工程学报，2014，47（4）：9—18.

LI F W，XIAO Y，ZHAO Y B.Experimental and analytical study on progressive collapse of RC frame with sudden side columns removal[J].China Civil Engineering Journal，2014，47（4）：9—18.（In Chinese）

[11]  PHAM A T，TAN K H，YU J.Numerical investigations on static and dynamic responses of reinforced concrete sub-assemblages under progressive collapse[J].Engineering Structures，2016，15（8）：35—46.

[12]  何庆锋，周超，易伟建.爆炸移除钢筋混凝土框架柱抗倒塌性能数值模拟[J].湖南大学学报（自然科学版），2016，43（11）：61—67.

HE Q F，ZHOU C，YI W J.Numerical simulation on collapse behavior of RC frames with a column removal under blast loads[J].Journal of Human University（Natural Sciences），2016，43（11）：61—67.（In Chinese）

[13]  OTHMAN H，MARZOUK H.Finite-element analysis of reinforced concrete plates subjected to repeated impact loads[J].Journal of Structural Engineering，2017，143（9）：1—16.

[14]  聂建国，王宇航.ABAQUS 中混凝土本构模型用于模拟结构静力行为的比较研究[J].工程力学，2013，30（4）：59—67.

NIE J G，WANG Y H.Comparison study of constitutive model of concrete in abaqus for static analysis of structures[J].Engineering Mechanics，2013，30（4）：59—67.（In Chinese）

[15]  GB 50010—2010 混凝土设计规范[S].北京：中国建筑工业出版社，2010：35—36.

GB 50010—2010 Code for design of concrete structures[S].Beijing： China Architecture & Building Press，2010：35-36.（In Chinese）

[16]  CEB-Fip model code 2010—First complete draft： volumn 1[S].Lausanne，Switzerland： FIB Bulletin，2010：763—777.

[17]  MALVAR L J.Review of static and dynamic properties of steel reinforcing bars[J].Materials Journal，1998，95（5）：609—616.

[18]  庄茁，由小川，廖剑晖，等.基于ABAQUS的有限元分析和应用[M].北京：清华大学出版社，2009：256—257.

ZHUANG Z，YOU X C，LIAO J H，et al. Finite element analysis and application based on ABAQUS[M].Beijing：Tsinghua University Press，2009：256—257.（In Chinese）