铰接车与非铰接车车-桥耦合系统振动特性的对比分析
丁 杰,丁旺才,严 波,卫晓娟
(1.兰州交通大学 机电工程学院,兰州 730070;2.中车株洲电力机车有限公司,株洲 412001)
0 引言
当列车通过桥梁时,机车车辆荷载通过轮轨关系、桥轨关系将荷载传递给桥梁,引起桥梁的振动和变形,桥梁的振动和变形也会反过来加剧车辆的振动响应[1]。因此研究车辆-线路-桥梁耦合的动力学性能具有重要的理论价值和工程实际意义。国内外众多学者陆续开展了车辆-线路-桥梁振动性能的研究。C.L.Dhar[2]将车辆简化为多刚体系统,研究了列车进桥时车桥系统的垂向振动情况。G.Diana[3]考虑弹性轨道和轮轨关系,建立了车辆-线路-桥梁动力学模型,仿真结果与实测结果基本一致。翟婉明[4]提出了车辆-轨道耦合动力学新理论,并在铁路工程中得到了广泛应用。李小珍[5]探讨了详细的车桥耦合关系,建立了车桥耦合系统控制方程,提出了方程求解的分离迭代技术。夏禾[6]等对车桥耦合系统在随机激励下的动力学行为进行了研究,并提出了上承式钢板梁桥的加固方案。
法国的TGV铰接式高速列车在技术上和商业运用上取得巨大成功后,德国、西班牙、韩国和中国等国家也纷纷加入了铰接式高速列车的研制和运营的行列之中。铰接式高速列车和非铰接式高速列车的运行性能的对比研究也得到了众多学者的关注。翟婉明[7]建立了铰接式高速列车-轨道垂向耦合动力学模型,对铰接式高速列车和非铰接式高速列车的垂向动力学性能进行了对比研究。研究结果表明,铰接式高速列车具有良好的垂向动力性能。王福天等[8]阐述了铰接式高速列车转向架的设计原则和设计思路,运用STUDYNA、MEDYNA和TPLDYN A三种软件对车组的运行稳定性、运行平稳性和曲线通过性能进行了计算。张楠等[9]建立了115个自由度的Thalys铰接式高速列车动力学模型和Antoing桥梁动力学模型,分析了列车的振动加速度和桥梁的挠度、加速度等动力响应,并与现场实测结果较好吻合。以上研究均采用数值积分的方法开展研究,但运用多体动力学软件对铰接式高速列车车-桥耦合系统振动响应的研究还比较少见。本文基于车-桥耦合关系,考虑列车在桥梁上高速运行的情况,运用多体动力学软件UM,分别建立了铰接车与非铰接车的三辆车编组列车模型和简支箱梁桥的车-桥耦合系统动力学模型,列车在桥梁上高速运行时,对列车和桥梁的动力学性能进行了对比 研究。
1 铰接车与非铰接车的结构特点
目前,国内运行的高速列车均为非铰接车车辆,两个转向架单独支撑每节车辆,车辆之间通过车钩连挂,车钩传递牵引力及冲击力,车辆之间的耦合作用并不明显。而铰接车高速列车除头车和尾车采用传统的动力转向架外,中间车辆使用铰接转向架,转向架支撑着前车的端部和后车的前部,中间车前后两端分别为支承端和铰接端,支承端端墙两侧各放置一个二系悬挂弹簧承台,中间为一个下球心盘座。铰接端无二系悬挂弹簧承台,中间放置一个上球心盘座。支承端的下球心盘座和铰接端的上球心盘座铰接在一起,铰接端车体的一部分垂向载荷通过球心盘座传递给支承端车体,再通过弹簧承台传递给空气弹簧及转向架构架。这样就相当于一个转向架支撑了一节车辆,使得列车中的转向架数量大大减少,减轻了列车的自重,同时列车的运行阻力和振动噪声也随着转向架数量的减少而大幅降低,但车辆之间通过中央弹性铰等紧密铰接,因此车辆之间的耦合作用较为明显。现有的铰接车转向架主要有铰接装置与摇枕相连的有摇枕结构和无摇枕结构两种。
2 车-桥耦合系统动力学模型的建立
本文建立的非铰接车模型的三节车体使用车钩连接,由六个转向架支撑;铰接车模型采用TGV无摇枕转向架结构,列车包括三节车体(一个铰接中间车体和两个端部车体),由四个转向架支撑。两种车型均是由车体、转向架和轮对组成的多刚体系统,按照体、铰、力元的步骤由下而上的顺序建模。在UM软件中建立几何外形时有在UM Input中直接建立和将SolidWorks、UG等三维CAD几何模型导入UM软件两种方式,铰接车与非铰接车的几何外形采用UM软件直接建立和三维模型导入UM软件相结合的方式[10]。力元(弹簧、阻尼器等)的几何外形通过UM直接建立,轴箱、构架、车体等几何外形通过外部导入的方式实现。两种车型的车轮滚动圆直径,滚动圆横向跨距一致,轴距相同,三辆车编组的铰接车与非铰接车列车动力学模型分别如图1和图2所示。

图1 非铰接车列车模型

图2 铰接车列车模型
桥梁选用跨度为32m的预应力混凝土双线整孔简支箱(单箱单室)梁桥,标准为通桥(2008)2322A-Ⅱ。在ANSYS中建立桥梁柔性体模型,通过ANSYS_UM程序生成input.fss文件,之后把生成的input.fss文件导入UM软件。双线整孔简支箱梁的一端安装一个固定支座和一个横向活动支座,另一端安装一个纵向活动支座和一个多向活动支支座。固定支座和纵向活动支座一般应该在梁的同一侧,横向活动支座与多向活动支座一般应在梁的另一侧,因此在调整好相关位置参数之后对桥梁模型设置相应的special forces力元约束,生成桥梁子系统。分别导入车辆子系统和桥梁柔性子系统,调整两子系统之间的相对位置,由于是运行双线的桥梁,使得车辆位于桥梁上线路一侧的相应位置。铰接车与非铰接车车-桥耦合系统动力学模型分别如图3和图4所示。

图3 非铰接车-桥耦合系统动力学模型

图4 铰接车车-桥耦合系统动力学模型
3 车-桥耦合振动特性对比分析
在仿真分析中,轨道采用C60钢轨,轨底坡为1/40,轨道不平顺为长波不平顺(波长20m,波深6 mm),车速为250km/h。铰接车与非铰接车车-桥耦合系统振动动态响应仿真结果如图5~图12所示。
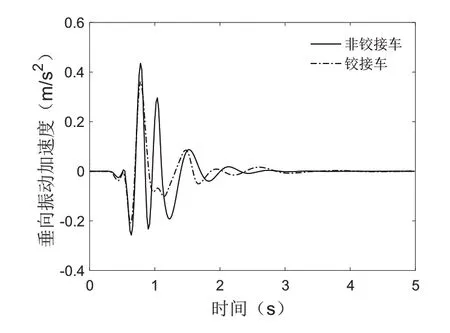
图5 铰接车与非铰接车尾车垂向振动加速度
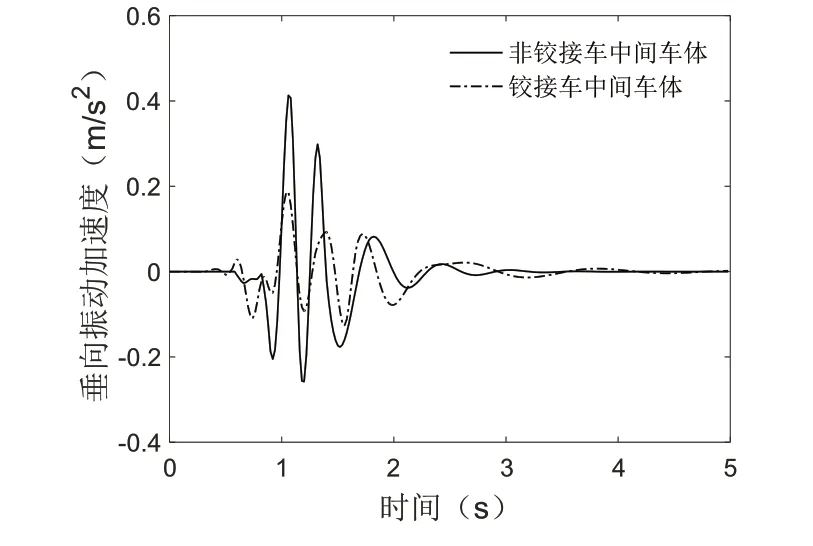
图6 铰接车与非铰接车中间车体垂向振动加速度
从图5可看出铰接车尾车垂向振动加速度较小于非铰接车的尾车,这是由于铰接车的尾车后端无其他车体的耦合约束,但在前端,尾车的振动受到中间车车体的耦合抑制,车钩耦合作用相对于非铰接车要强烈一些。从图6中可看出铰接车中间车体的垂向振动加速度明显小于非铰接车的垂向振动加速度,铰接式列车的转向架置于相邻两车之间,车与车之间设置有减振器,中间车的振动受到两侧的耦合抑制,车体间的耦合作用较强,车体振动相互抑制削弱;而非铰接车的中间车两侧通过车钩与端部车连挂,受到的耦合抑制作用要小。
为了验证铰接车纵向耦合作用强弱对车体振动加速度的影响,就纵向减振器对铰接车的头车和中间车的振动加速度进行对比分析。从图7可以看出,有无纵向减振器下铰接车的头车振动加速度大小基本相同,纵向阻尼对铰接车的头车振动加速度的影响较小。图8可以看出,无纵向减振器的情况下,铰接车中间车的垂向振动加速度明显增大,说明铰接车之间的纵向减振器对抑制中间车车体振动有明显的作用。结合图7和图8进一步分析可知,头车车体只有尾端有纵向阻尼,单侧阻尼对车体振动的抑制作用并不明显;而中间车车体两端都有纵向阻尼,两侧阻尼所产生的对振动的抑制作用有很明显的效果。
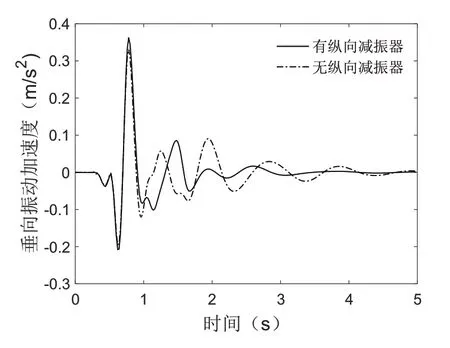
图7 纵向阻尼对铰接车头车振动的影响
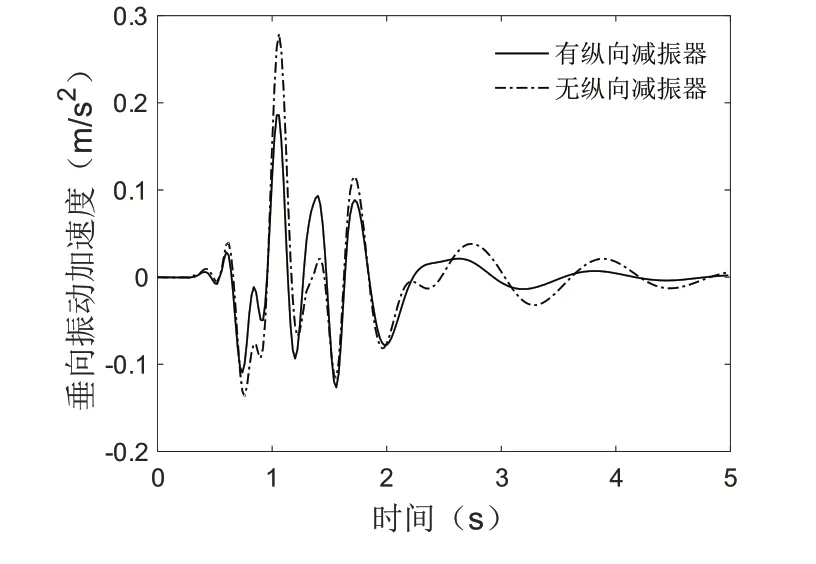
图8 纵向阻尼对铰接车中间车振动的影响
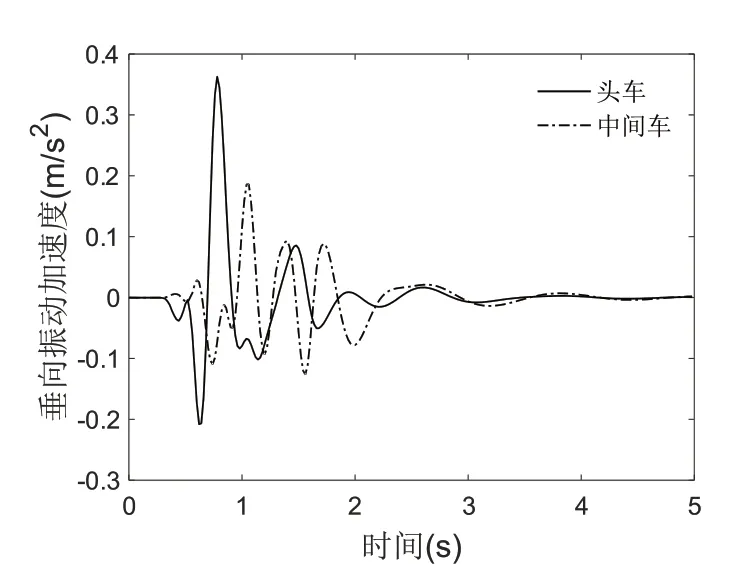
图9 有纵向阻尼时铰接车头车与中间车振动对比
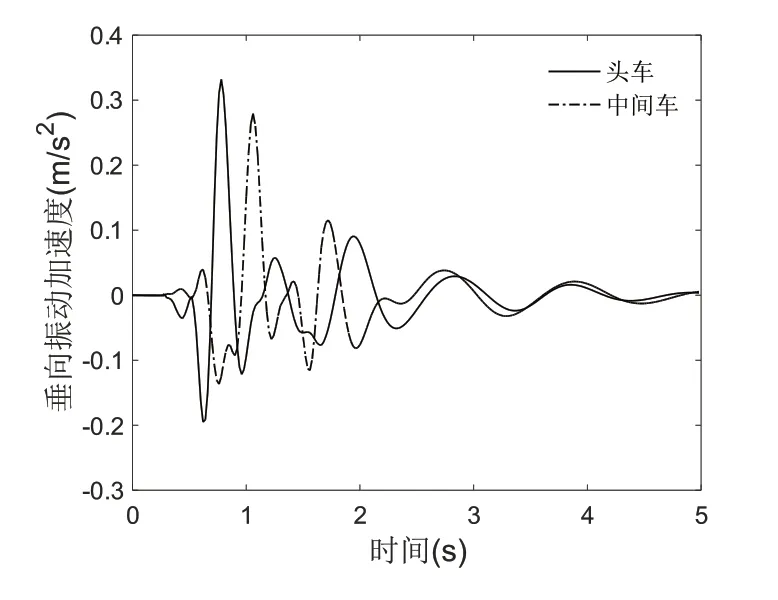
图10 无纵向阻尼时铰接车头车与中间车振动对比
图9显示铰接车头车的振动比中间车大一些,体现了铰接式列车在车体加速度的分布上,呈两端大、中间小趋势的规律。图10是铰接车去掉纵向减振器的情况,此时中间车的垂向振动加速度明显增大,与头车的垂向振动加速度已经比较接近,但是还是小于头车的振动加速度,这与非铰接车呈现的结果是一致的,端部车的垂向振动加速度一般都大于中间车。一般情况下,无论是铰接车还是非铰接车,中间车的振动都有弱于端部车,中间车的舒适性好于端部车;铰接车的中间车的舒适性一般要好于非铰接车,铰接式连接可以增加列车的稳定性,能有效降低车体的振动。

图11 桥梁跨中垂向振动加速度
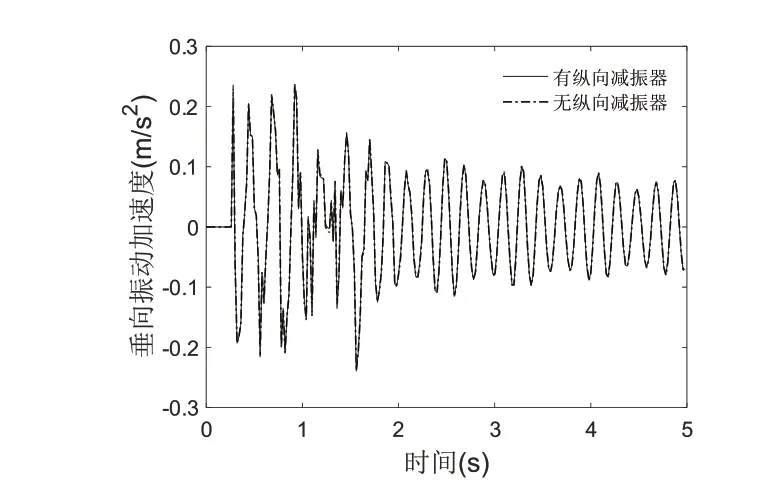
图12 铰接车有无纵向阻尼下桥梁跨中垂向振动加速度
桥梁跨中竖向振动加速度限值是[a]max=0.35g(有柞轨道桥梁),[a]max=0.50g(无柞轨道和明桥面桥梁),图11显示非铰接车激励下的桥梁垂向振动加速度略大于铰接车,铰接车激励下的振动衰减的较快,但两种情况下的桥梁跨中振动加速度相差较小,因此铰接车和非铰接车对桥梁的垂向振动的影响作用基本相当,桥梁的动力学指标均在安全范围以内,且具有很大的安全余量。从图12可以看出,铰接车有无纵向减振器对桥梁跨中垂向振动几乎无影响,说明纵向减振器对车辆与桥梁间的耦合作用影响有限,车体间的耦合作用强弱与桥梁振动的响应基本不相关,也正说明图11中两种情况下桥梁跨中垂向振动加速度的不同并不是车体间纵向阻尼引起的,而是由车辆本身的性能参数所决定。
4 结语
本文运用多体动力学软件UM分别建立三节铰接车、三节非铰接车模型与简支箱梁桥的车桥耦合系统动力学模型,对铰接车与非铰接车的车桥振动特性做了对比分析,进而仿真分析了铰接车有无纵向减振器时的车桥振动特性,得到了以下结论:
1)端部车的垂向振动强于中间车的垂向振动。铰接车的中间车车体垂向振动明显小于非铰接车中间车车体,铰接车中间车的舒适性一般好于非铰接车中间车。
2)铰接车的主要优点是车体间的阻尼加强了车体间的耦合作用,中间车车体振动得到一定的有效抑制,使得中间车受耦合抑制较强而振动较弱,但对于头车和尾车来说阻尼所起到的抑制作用较为有限,有无纵向减振器对车辆振动程度的影响较小。
3)铰接车与非铰接车作用下桥梁的跨中垂向振动基本相同,车体间耦合作用的强弱对桥梁的垂向振动影响有限。

