基于改进熵权TOPSIS模型的岩质边坡稳定性评价

姜安民，董彦辰，刘 霁，倪 佳

(1.湖南城建职业技术学院，湖南 湘潭 411100；2.中南林业科技大学 土木工程学院，湖南 长沙 410004；3.湖南大学 土木工程学院，湖南 长沙 410082)

边坡是一个非线性的、不确定的动态系统，受多因素影响[1]。边坡稳定与否关系重大，在失稳状态下不仅会带来巨大的经济损失，同时还威胁着人们的生命安全。如何快速、准确的对岩质边坡稳定性进行评价一直是研究的重点。针对边坡稳定性评价问题学者们做了大量研究，如：张军等[2]基于云模型，对岩质边坡稳定性进行评估，并验证了该方法的可行性与有效性；王新民等[3]建立层次分析法-可拓学模型，对岩质边坡稳定性安全进行评价，并得出该方法与RMR(Relative Metabolic Rate)法和BQ(Basic Quality)法计算的评价结果一致的结论；宋鑫华等[4]将蝴蝶突变理论在边坡稳定性评价中加以应用，指出了该方法避免了传统判断方法的主观性问题；黄建文等[5]采用基于AHP(Analytic Hierarchy Process)的模糊评判法对边坡稳定性进行评价，通过工程实例验证了模型的正确性；赵建军等[6]基于因子分析法对边坡稳定性评价指标进行计算，并对指标重要性进行排序；王广月等[7]基于粗糙集理论对边坡稳定性评价中各因素权重确定方法进行研究，指出了该方法的优势；张菊连等[8]建立了Logistic回归模型对边坡稳定性进行评价，并验证了该方法推广的可能性。李元松[9]、周宁[10]采用模糊神经网络对边坡稳定性进行评价，并取得了较好的效果等。

对前人研究成果进行学习、借鉴，并归纳总结得如下问题：(1)部分评价方法计算复杂，评价过程繁琐；(2)在评价过程中，传统的单一赋权方法很难保证评价结果的准确性，有待改进；(3)一些评价方法在应用中缺少对比、验证，评价方法的可靠性有待商榷。

本文采用改进的TOPSIS(Technique for Order Preference By Similarity to Ideal Solution)模型对岩质边坡稳定性进行评价，本方法操作简单，不需要复杂的计算过程，评价结果不仅能反映边坡所处的稳定等级，还可以体现对临近等级的贴近情况；在权重计算过程中，采用熵权对主观权重进行修正，避免了单一赋权法存在的缺陷；采用灰色关联模型、可拓模型对评价结果进行检验，得出了相一致的结论，验证了该方法的可靠性。

1 岩质边坡稳定性评价指标体系

影响岩质边坡稳定性的因素较多，不同学者在研究过程中选取的评价指标有所差异。如：王新民等[3]将评价指标体系分为地址条件、环境条件、工程条件三大方面，其中包括单轴抗压强度、弹性模量、泊松比、岩体结构特征等十三个评价指标；黄建文等[5]选取了工程地质特征、地形地貌特征、水文气象特征及其他因素特征等四个一级评价指标，岩土类型、结构面发育程度、内摩擦因数等十二个二级评价指标进行研究；赵建军等[6]选取了坡度、坡高、岩性、边坡结构等七个指标进行评价。通过以上介绍可以看出，影响边坡稳定性的因素有十余个，本文在建立评价指标体系过程中，充分考虑各指标对边坡稳定的影响程度，并参考相关文献[11～13]，同时遵循指标体系可操作性强、指标易量化、能够客观反映边坡稳定程度的基本原则，建立了一套相对完善且可操作性强的评价指标体系。本评价指标体系中选取了岩石质量指标(Rock Quality Designation,RQD)、岩石完整性指标、地应力等七项指标，详见表1。

2 改进熵权TOPSIS边坡稳定性评价模型

TOPSIS即“逼近理想解排序方法”，是基于多项指标的多方案分析比选方法，该方法于1981年由Hwang和Yoon提出[14]。TOPSIS法能够客观全面地反映岩质边坡稳定程度的动态变化，岩质边坡稳定性程度可以通过测量目标距离正理想解和远离负理想解的程度来进行评估。在传统TOPSIS法中，可以通过各方案与最优方案的贴近程度来判断方案的优劣，但无法对各方案的好坏量化后定级评价，在本研究中，为了将岩质边坡稳定程度进行量化判断并定级，对传统TOPSIS法进行改进，基于熵权法构建改进TOPSISI边坡稳定性评价模型，具体操作如下。

2.1 岩质边坡稳定性等级划分

为验证评价结果的准确性，本文采用文献[11]中岩质边坡稳定性分类标准，具体等级划分见表2。

对表2中数据进行无量纲处理，具体结果见表3。

2.2 建立初始判断矩阵

结合待测边坡实际情况，建立待测边坡集，P={P1,P2,…,Pm}，该待测边坡集包括PⅠ～PⅤ(PⅠ～PⅤ表示五个待测等级，待测指标值取区间下限值，详见表8)，各待测边坡评价指标集r={r1,r2,r3,…,rn}，根据评价指标集建立初始判断矩阵如下：

(1)

式中：rij代表第i个边坡的第j个评价指标初始判断值，i∈[1,m]，j∈[1,n]。

2.3 决策矩阵标准化

由于评价指标具有不同的量纲及量纲单位，为消除指标不可公度性，进行无量纲化处理。评价指标可分为收益型及消耗型两种，收益型指标越大越好，消耗型指标则越小越好，无量纲处理[11]后得到标准化决策矩阵，具体如下：

(2)

(3)

(4)

2.4 加权标准化决策矩阵

2.4.1 求解评价指标权重

(1)AHP

AHP[15](Analytic Hierarchy Process)即层次分析法，20世纪70年代由美国运筹学家Saaty,T.L.提出，AHP是一种层次权重决策分析方法，具体操作如下：

1)建立层次结构模型

通常包括目标层、中间层及准则层三个层次。

2)构造判断矩阵

将各指标重要程度进行比较，构造判断矩阵A=(aij)n×n，在本文中采用1-9标度法对比较结果进行量化，具体规则见表4。

表4 AHP量化规则

3)层次单排序及一致性检验

计算一致性指标CI，计算如下：

(5)

式中：λmax为判断矩阵的最大特征值。

查找一致性指标RI，见表5。

表5 平均随机一致性指标

计算一致性比例CR，计算如下：

(6)

当比值小于0.1时，一致性检验通过，否则进行修正。

4)层次总排序及一致性检验

同样，CR小于0.1时，一致性检验通过，否则进行修正。

5)权重计算

AHP计算权重的方法不唯一[16]，主要有几何平均法、算数平均法、特征向量法等，几种方法计算权重的值较为接近，本文中采用特征向量法，具体操作如下：

Aω=λmaxω

(7)

式中：λmax为判断矩阵A的最大特征值；ω为与之对应的特征向量；将特征向量归一化处理，即得到各项指标权重值ωi。

(2)熵权法

熵是一种不确定性的定量化度量，最先由Shannon，C.E.将原本热力学概念的熵引入信息论，称之为信息熵，熵权法是计算客观权重的常用方法，具体步骤如下[17～19]：

1)建立原始数据评价矩阵K

K=(kij)n×m

(8)

式中：kij为指标初始评价值。

2)归一化处理判断矩阵K，得到标准矩阵P

P=(pij)n×n

(9)

(10)

3)计算信息熵

(11)

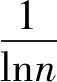
4)计算指标信息熵权重

(12)

进而，得到客观权重向量：

β=(β1,β2,β3,…,βn)

(13)

(3)优化组合赋权模型

在对确定岩质边坡稳定性进行评价过程中，评价指标权重的计算至关重要，为弥补单一赋权存在的缺陷，采用AHP确定指标主观权重ωi，采用熵权法确定评价指标客观权重βi，通过熵权对主观权重进行修正，得到最终权重zi。本文根据最小熵原理将主客观权重进行组合，具体如下[20]：

(14)

式中：ωi为主观权重；βi为客观权重；zi为组合权重；n为系统指标个数。

采用拉格朗日乘子方法求解组合权重，求得zi如下：

(15)

2.4.2 加权标准化决策矩阵

加权标准化决策矩阵计算如下：

(16)

2.5 贴近度分析

对于收益性指标集J1取各方案中该指标的最大值，消耗性指标集J2的取值与之相反，具体如下：

(17)

(18)

式中：F+表示为正理想解，F-表示为负理想解。各评价方案与理想解的距离用下式表示：

(19)

(20)

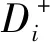
贴近度分析见下式：

(21)

贴近度分析结果具体解释，见表6[21]：

表6 贴近度分析结果解释

2.6 岩质边坡稳定性判断

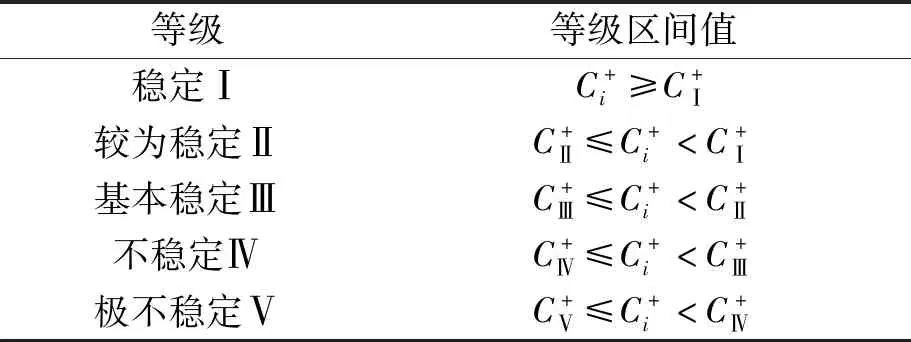
表7 岩质边坡稳定性评判规则

3 工程算例

3.1 决策矩阵标准化

为验证评价结果的可靠性，选取渝黔高速公路某段边坡P1为验证组，结合文献[11，22]评价结果进行对比。选取湘西地区某高速公路三段边坡P2,P3,P4为评价组，该地区为丘陵地貌，地质条件复杂，三段边坡坡高均在30 m以上，坡角在50°～70°之间，日最大降雨量均超过150 mm。将各组数据进行无量纲处理，见表8。

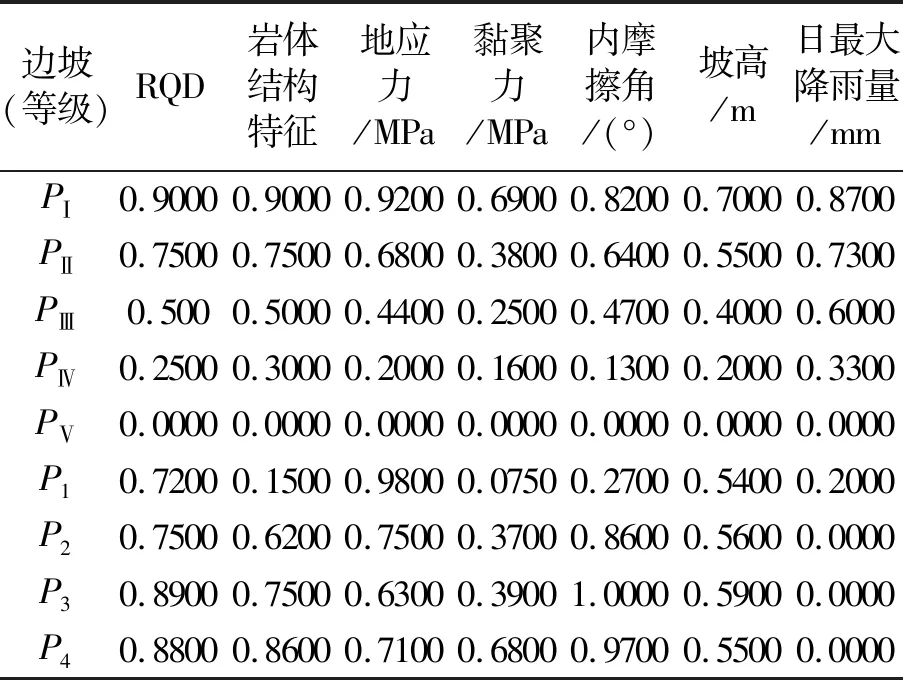
表8 边坡稳定性指标等级与实测值(无量纲)

得标准化决策矩阵如下：

B=(bij)m×n=

3.2 加权标准化决策矩阵

(1)求解评价指标权重

运用AHP计算主观权重过程中，首先应将评价指标两两比较，根据相对重要程度(表4)建立判断矩阵。在本研究中邀请了10位专家(6位来自高等院校，4位来自勘察设计单位，均具有副高及以上职称，其中注册岩土工程师5人)通过问卷调查形式建立判断矩阵。第一轮问卷调查确定各指标间的相对重要性，第二轮问卷调查确定指标间的相对重要程度，对出现的不一致现象进行动态调整，最终获得评价指标相对于目标层的判断矩阵，见表9。

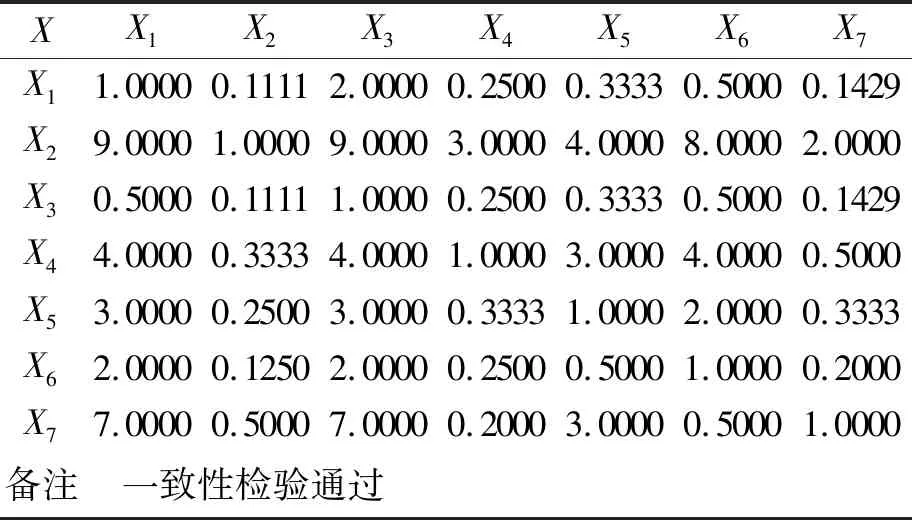
表9 评价指标相对于目标层判断矩阵

根据判断矩阵，计算各指标主观权重值如下：

ω=(0.0381,0.3830,0.0311,0.1616,0.0879,0.0518,0.2464)

根据式(8)～(13)，计算客观权重值如下：

β=(0.1112,0.1157,0.0815,0.2130,0.1311,0.1871,0.1604)

根据公式(14)，(15)，计算组合权重如下：

Ζ=(0.0711,0.2298,0.0550,0.2025,0.1172,0.1075,0.2170)

将主观权重值与熵权修正后权重值进行对比，见图1：

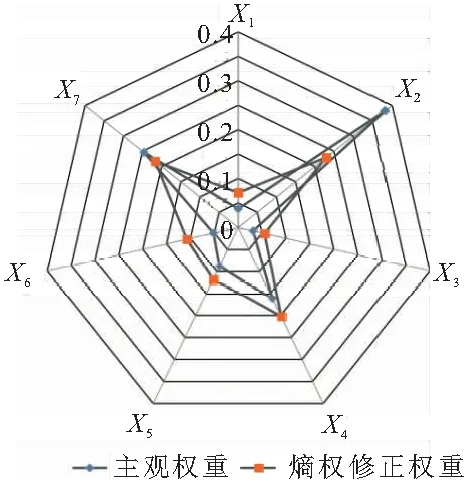
图1 主观权重值与熵权修正权重值比较

通过比较可以看出，熵权对各指标主观权重可以在一定程度上进行修正，避免了主观意愿过强引起的权重偏差。

加权标准化决策矩阵如下：

F=(fij)m×n=

3.3 贴近度分析

根据加权标准化决策矩阵，得正理想解、负理想解如下：

F+=(0.0640 0.2068 0.0539 0.1397 0.1172 0.0753 0.1888)

F-=(0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000)

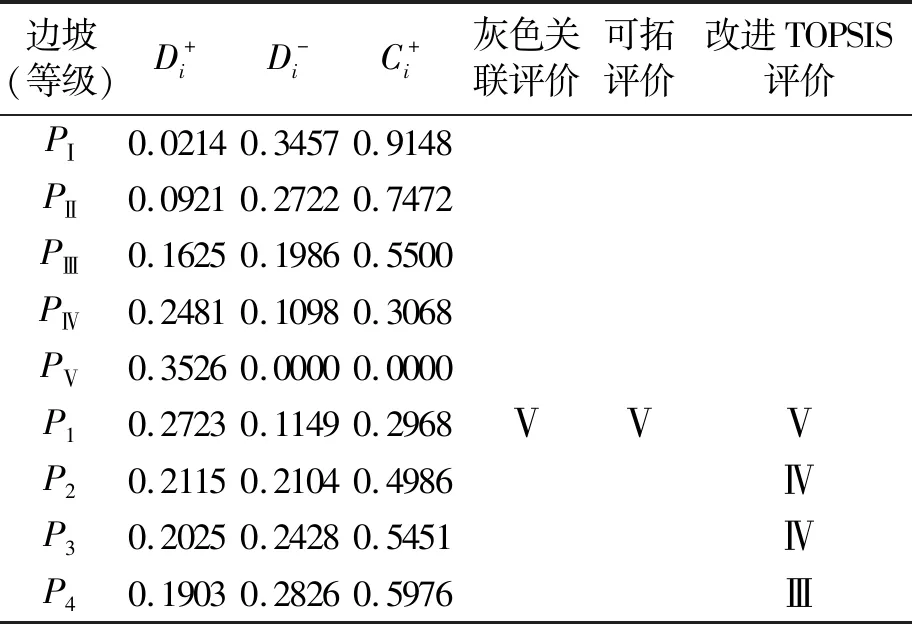
表10 各边坡贴近度及评价等级

3.4 结果分析

4 结 论

(1)对岩质边坡稳定性评价的若干方法进行分析，归纳总结了研究过程中存在的一些不足，如：评价方法计算复杂，评价过程繁琐；单一赋权方法很难保证评价结果的准确性；评价方法在应用中缺少对比、验证等。

(2)对传统TOPSIS模型进行改进，该方法在岩质边坡稳定性评价中操作简单、无需复杂的计算过程，评价结果在反映边坡所处稳定等级的同时，还可以体现对临近等级的贴近情况；在权重计算过程中，基于最小熵原理，采用熵权对主观权重进行修正，避免了单一赋权法存在的缺陷。文献[22]提出评价指标具有动态变化特征，即权重随指标数值变化而改变，该赋权理念值得参考，可以作为权重继续改进的方向。

(3)基于改进熵权TOPSIS模型，选取P1,P2,P3,P4四段边坡进行稳定性评价，并得出所处等级分别为Ⅴ级、Ⅳ级、Ⅳ级、Ⅲ级，即极不稳定、不稳定、不稳定、基本稳定的结论，稳定性好坏排序为：P1