随风潜入夜,“顿悟”巧发生
江苏省通州湾三余初级中学 姜海平
新课程标准认为学生是学习的主人,因此教师要重视他们的自主学习,重视他们独特的思考过程感受和思维迸发的体验。因此,启发“顿悟”发生的初中数学课堂成了学生生成素养的理想课堂。一般地,让“探究在先,合作在后”“学的前移,而教的后置”等学习方式,都是“顿悟”产生的绝佳时机。
一、在情境中,给“顿悟”提供画面
心理学家研究表明,在熟悉的情境里,人们的思维更活跃,从顿悟中能催生新的认知。现在的班级基本是一个大熔炉,各地方的学生都有。而不同地域的学生接触的事物往往不同,教师呈现的情境就应该是他们比较了解的甚至是比较熟知的。教师在设置情境时,可以用学生熟悉的认知进行导入。比如在讲勾股定理时,教师设置这样的情境:据说科学家准备将勾股定理作为与外星人进行交流的暗号,你能将这一暗号运用到下面这道题当中吗?学生对外星人的相关传闻有所了解,这是旧知;对勾股定理,特别是对它的运用不是很了解,这是新知。这样的情境足以调动学生解题的兴趣,它既告诉学生勾股定理的重要性,也提醒学生这题的思维焦点。“问题是接生婆,它能帮助新的思维的诞生”,但情境要有一个从“旧”向“新”漫溯的过程,以这题为例:现有长方形纸片一张,长19cm,宽15cm,需要剪去边长多少的小正方形,才能做成底面积为77cm2的无盖长方体的纸盒?教师先让学生拿出一张纸片,按照要求裁剪成题目中的样子,然后再控制好尺寸,做成一个盒子。这样题目就变成了情境题,给学生“顿悟”提供真实的画面,要求边长,学生先将边长设为xcm,这是他们练习数学时的一个定势思维。当学生看着折叠的盒子,他们很快就能推测出新的长和宽,这个“顿悟”在有了具象之后就一目了然了。
学生列出方程为(19-2x)(15-2x)=77,最终算出结果,当x=13时,19-2x<0,他们看着情境,也知道不符合题意,因而就剩下x=4。情境给“顿悟”的时间,也给学生思维转换的空间。“顿悟”是学生慢慢揣摩的过程,是他们将推测付诸实施的过程。情境在某种程度上可以验证“顿悟”的结果,同时也会让学生在日后的学习中将情境印入头脑,不需要具体的操作就会浮现在他们眼前。
二、在合作中,给“顿悟”提供帮助
现在对数学的考查大多集中在对学生素养与能力的测试,因而问题具有开放性,自然也就有一定的难度,教师可以结合学生的认知规律安排小组讨论,做到人人能有话说,人人参与,这样可防止个别优生的思维代替其他学生思维,进而使所有学生在认识上都有一个“顿悟”的过程,都能迸发智慧的火花。要想让“顿悟”实实在在地在每个学生身上发生,教师就要组织好、引导好讨论, 做到及时反馈。讨论的过程也是酝酿“顿悟”的过程。讨论的过程也是学生合作的过程,思维碰撞的过程,也是学生产生新思维的过程。讨论当然离不开教师的指导,因此不能盲目地出示问题后就让学生讨论,这样会变成学生的自言自语,或者成为好生的个人表演。老师要有计划地参与小组的讨论,在思考方法、提问方法、意见方法等方面加以指导,长期下去,学生便能掌握讨论方法,讨论技巧,从而使“顿悟”更好地形成。已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC。(1)求证△ACE≌△BCD; (2)猜想△DCE是什么三角形。
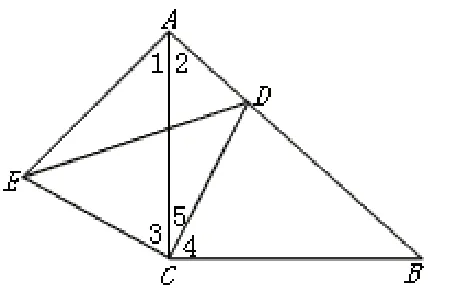
对于第一问,不再赘述。说一说第二问的“顿悟”过程。当学生将题目中涉及的角用数字一一标出来之后,在小组讨论的过程中他们发现这很有可能就是等腰直角三角形。因为在第一小题中已经证明了边相等,题目中又出现了直角三角形,这个三角形可能也是。小组合作集中了集体的智慧,也让“顿悟”能走上思维的快车道,在提高解题效率的同时,为之后题目中的“顿悟”提供更多思路。合作之后,就是学生自我解题的过程,学生说因为△ACE≌△BCD,所 以CE=CD,∠3=∠4,因 为∠4+∠5=90 °,所 以∠3+∠5=90°,所以∠ECD=90°。
三、在追问中,让“顿悟”走向深刻
让学生顺着问题的脉络自己去寻找可能的结论。传统的习题总是规定好结果,让学生进行演算,或者证明,答案往往都是唯一的,但为了加强对学生思维灵活性的训练,教师可以设置开放性的问题。让学生自己去寻找问题,或者在问题中让学生自己去寻找答案。这给学生思维放飞的空间,给适合“顿悟”生长的土壤。在学生解决完一个问题之后,教师可以接着追问一个问题,使“顿悟”继续发生。在学生回答不出问题之后,教师可以补问一个问题,让问题进一步明晰,进一步对接学生的能力范围。比如说教师在讲解梯形的时候,先提出这样一个问题:两个完全一样的梯形可以拼成一个平行四边形吗?学生在座位上比划的同时,教师抛出第二个问题,拼成的平行四边形的高和原梯形的高有什么关系?学生继续“顿悟”,学习走向深层,问题由表及里。接着教师又问:拼成的平行四边形的底和原梯形的哪两条线段有关?拼成的平行四边形的面积和原梯形面积有什么关系?每一个问题都是在原有问题上的一次升华,都是为了让学生在“顿悟”的过程中不至于停留在事物的表面,都是让学生养成深层思维的习惯。学习数学最终目的不是为了解题,而是要在解题的过程中优化思维品质。
“顿悟”就是学生处于“愤悱”的状态,在似懂又非懂,在有所知又非全知的状态下,通过给学生做铺垫,调动其学习的主动性, 发展其思维的核心素质。因此,“顿悟”就是在学生掌握数学思维基础认知之后,形成基本方法,进而提升思维的品质,即,顿悟的过程也是直观和感性思维、理性和科学思维、逆向和批判思维发展的过程。

