一种控制力矩陀螺用双频驱动的超声电机

唐洪权，潘 松，陈 雷，徐张凡,徐洪波

(1.南京航空航天大学 机械结构力学及控制国家重点实验室，江苏 南京 210016; 2.淮柴动力扬州柴油机有限责任公司，江苏 扬州 225008)

0 引言

控制力矩陀螺是利用陀螺原理控制航天器姿态的设备，广泛用于各种人造卫星、宇宙飞船[1]等。控制力矩陀螺主要由产生角动量的高速组件、框架、驱动框架旋转的低速组件及相关控制电路组成[2]。现有控制力矩陀螺的低速组件一般由电磁电机、制动机构、减速齿轮构成[3]。该系统整体结构复杂,体积大,抗电磁干扰能力弱,不易实现高精度控制。

超声电机是一种利用逆压电效应、弹性体振动和摩擦传动原理的新型电机。与一般电磁电机相比，超声电机具有低转速、大扭矩、断电自锁、抗电磁干扰、瞬态响应快及定位精度高的优点。目前已广泛应用于航空、航天、医疗等领域[4]。

该研究课题面向微型卫星的姿态控制，要求单框架控制力矩陀螺(SGCMG)输出扭矩为0.1 N·m。由文献[5-6]可知,现有普通旋转行波电机的定子采用粘胶工艺，但胶水在高辐射、高真空、高温差的太空环境下，可能会发生胶水老化失效，不能满足控制力矩陀螺长期稳定地在太空环境中工作的要求；根据文献[7-8]，现有直线超声电机虽然能满足工作要求，但质量和体积过大；文献[9-11]中,其他形式的直线型超声电机在控制力矩陀螺上不易安装。为解决该问题，作者在刘振设计的矩形超声电机[12-13]基础上，重新设计了一种异型模态超声电机,用于驱动力矩陀螺框架旋转。

本文使用有限元分析软件ABAQUS对定子进行了有限元分析及尺寸优化，并加工制作了多台样机。设计了超声电机性能测试平台，完成了超声电机速度特性和负载特性的测试，并进行了结构优化。

1 超声电机结构

图1为该项目设计的单框架控制力矩陀螺，该结构采用并联机构，超声电机并联驱动力矩陀螺框架旋转。根据陀螺效应，动量轮的转动惯量为J，角速度ω2，通过控制电路使低速组件驱动框架转轴以角速度ω1旋转，通过改变高速组件的角动量矢量J·ω2而实现对外输出力矩M=ω1×(J·ω2)。

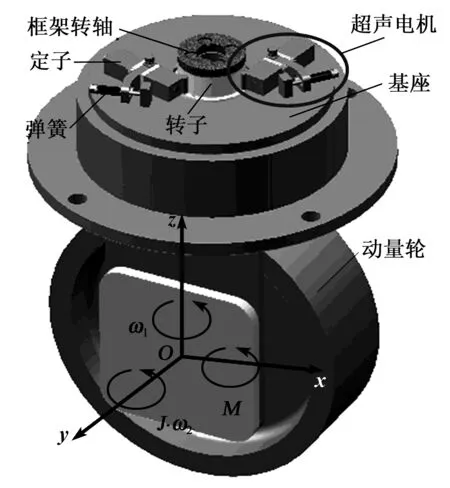
图1 超声电机安装结构图

超声电机结构简单，它由控制力矩陀螺基座、耐磨陶瓷套于框架转轴上组成的转子、超声电机定子及弹簧预压力施加装置构成。耐磨陶瓷由Al2O3加工而成。超声电机通过定子驱动耐磨陶瓷旋转,从而带动整个力矩陀螺框架旋转；预压力施加机构通过调节螺栓压缩弹簧行程调整预压力。该控制力矩陀螺可以根据设计目标要求，合理地增减并联超声电机数量。

2 超声电机定子的设计

2.1 定子结构

超声电机定子的分解图如图2所示。弹性体、压电陶瓷、电极片相对支架呈镜像布置，定子各个零部件通过螺栓锁紧。定子采用该布局使用压电陶瓷的d33效应。压电陶瓷的极化方向如图2所示，每片陶瓷被中间绝缘区域一分为二，每片压电陶瓷的两个极化分区的方向相反，通过“+”或“-”标明极化方向。定子由两路电信号A极和B极共同驱动且共地。

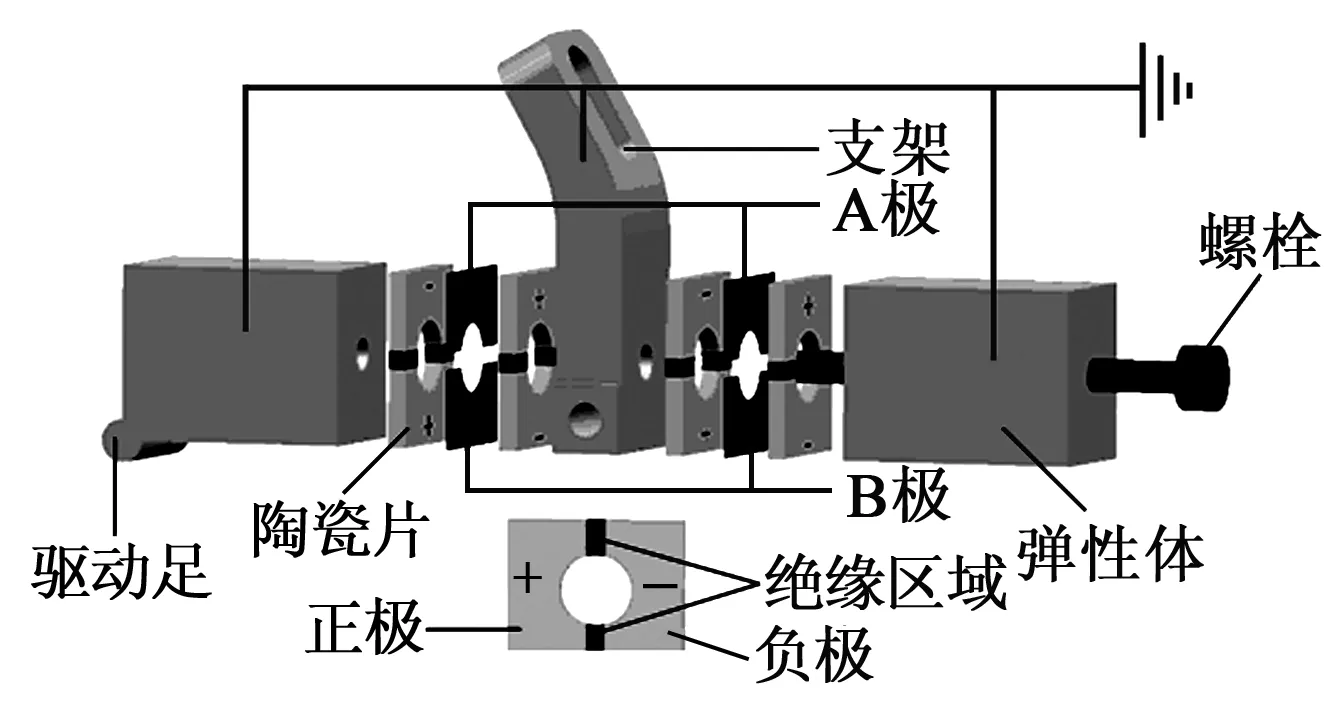
图2 定子结构爆炸图

2.2 振动模态及激励机制

该超声电机为单模态双频电机，定子采用单模态设计。即该电机仅通过一阶弯振或一阶纵振模态即可实现电机的旋转；双频指该电机使用不同的2个频率驱动以实现电机的正转和反转。2个振动模态如图3所示。

图3 定子振动模态

3 有限元分析

3.1 模态分析

电机定子模态分析使用有限单元法，通过有限元计算软件ABAQUS完成各个模态频率的计算[12]。弹性体、支架和驱动足均采用45#钢，弹性模量为200 GPa，泊松比为0.3，密度为7.85 g·cm-3；压电陶瓷采用PZT-8板并沿厚度方向分区极化。

该型超声电机为单模态双频驱动电机，考虑到该电机的工作模态为一阶弯振和一阶纵振模态，使用有限单元法进行模态分析时，为了避免出现模态混叠现象。需要考虑一阶弯振模态及其相邻振动模态和一阶纵振模态及其相邻振动模态[13]。

使用ABAQUS进行有限元分析前，该模型的有限元网格划分如图4所示。图中，H为定子弹性体长度，a为定子弹性体宽度，b为定子弹性体厚度。陶瓷片厚为1 mm。通过改变上述有限元计算模型中的这些尺寸以获得相关振动模态及频率。

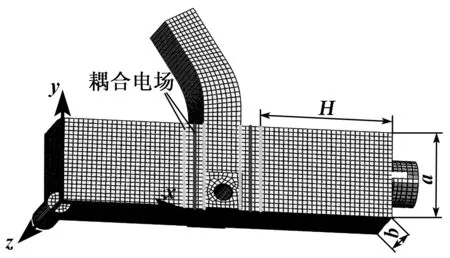
图4 定子有限元模型

3.2 谐波分析

该超声电机为单模态超声电机，几乎在任何尺寸下均可工作，优化尺寸的目标是在满足驱动陀螺框架的情况下尺寸最小化，在进行谐波计算时，激励电信号为幅值有效值100 V的正弦波，材料阻尼恒定为0.001。H,b,a对频率的影响如图5～7所示。

图5 H对2种振动模态频率的影响

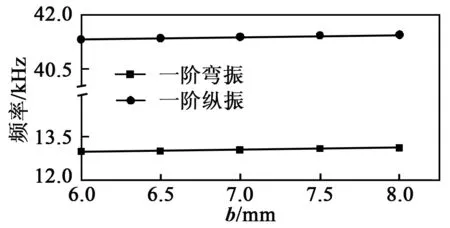
图6 b对2种振动模态频率的影响

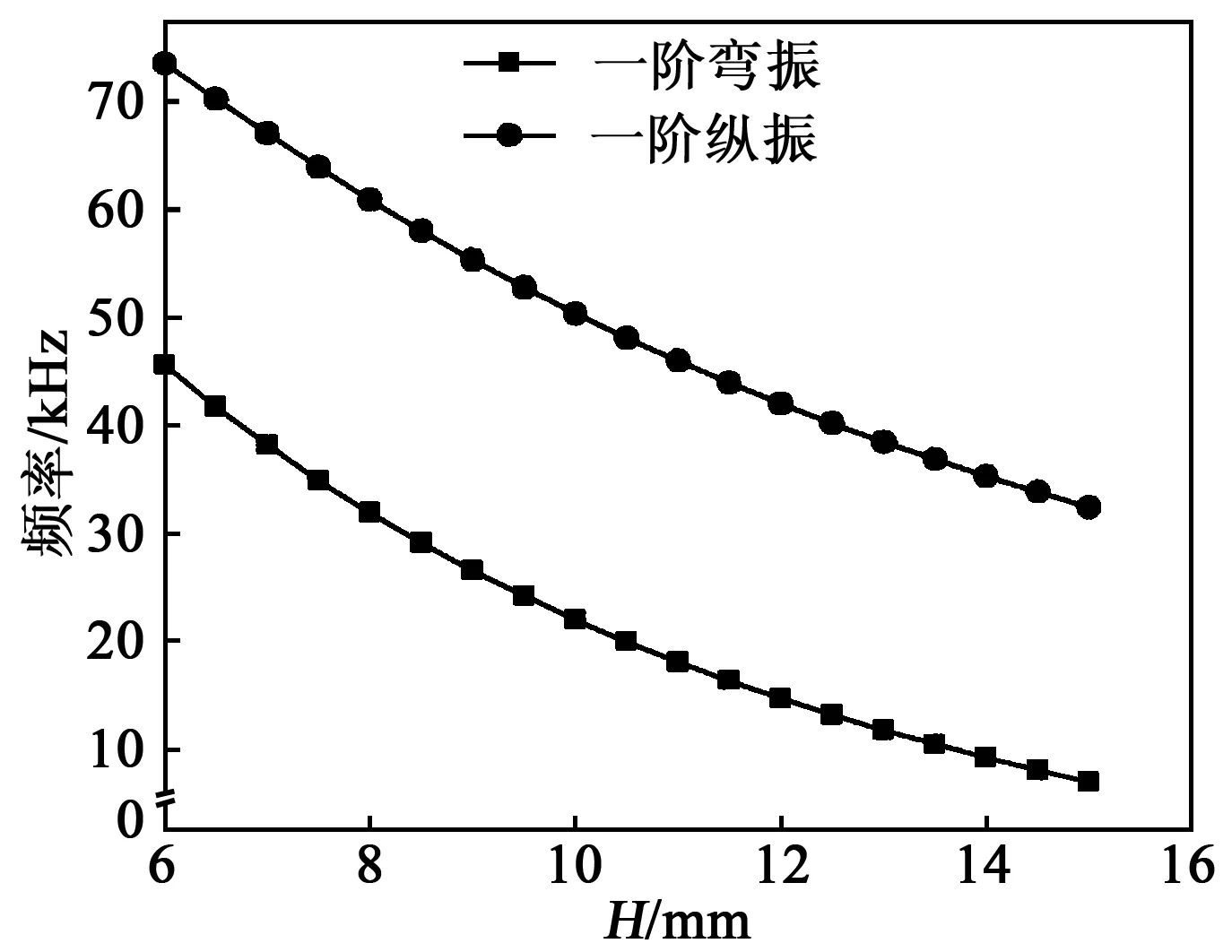
图7 a对2种振动模态频率的影响

3.3 运动机理

该超声电机为异型模态电机，通过切换激振电信号频率，改变定子振动模态，实现电机的双向转动[14]。为详细解释其运动机理，分别绘制了该电机定子在2种振动模态下的运动轨迹(见图8、9)。驱动足的运动轨迹分解成2个正交运动：对转轴的正应力FN及由正应力产生的摩擦力f。θ是f与电机下端面夹角，即安装角。FN和f的大小与驱动足的位移相关。f的方向和驱动足接触点处速度v与转轴接触点处切向速度u相关：

1)v和u同向且|v|>|u|，f与u相同且做正功。

2) 其他情况，f与u相反且做负功；由此可知：

a.超声电机的转动在微观上是一个间歇性运动。

b.超声电机在单个运动轨迹中，超过一半轨迹做负功。

c.驱动足正向作用时FN大于反向作用时的FN，同时正向作用时的f做功大于反向作用时的f的做功。

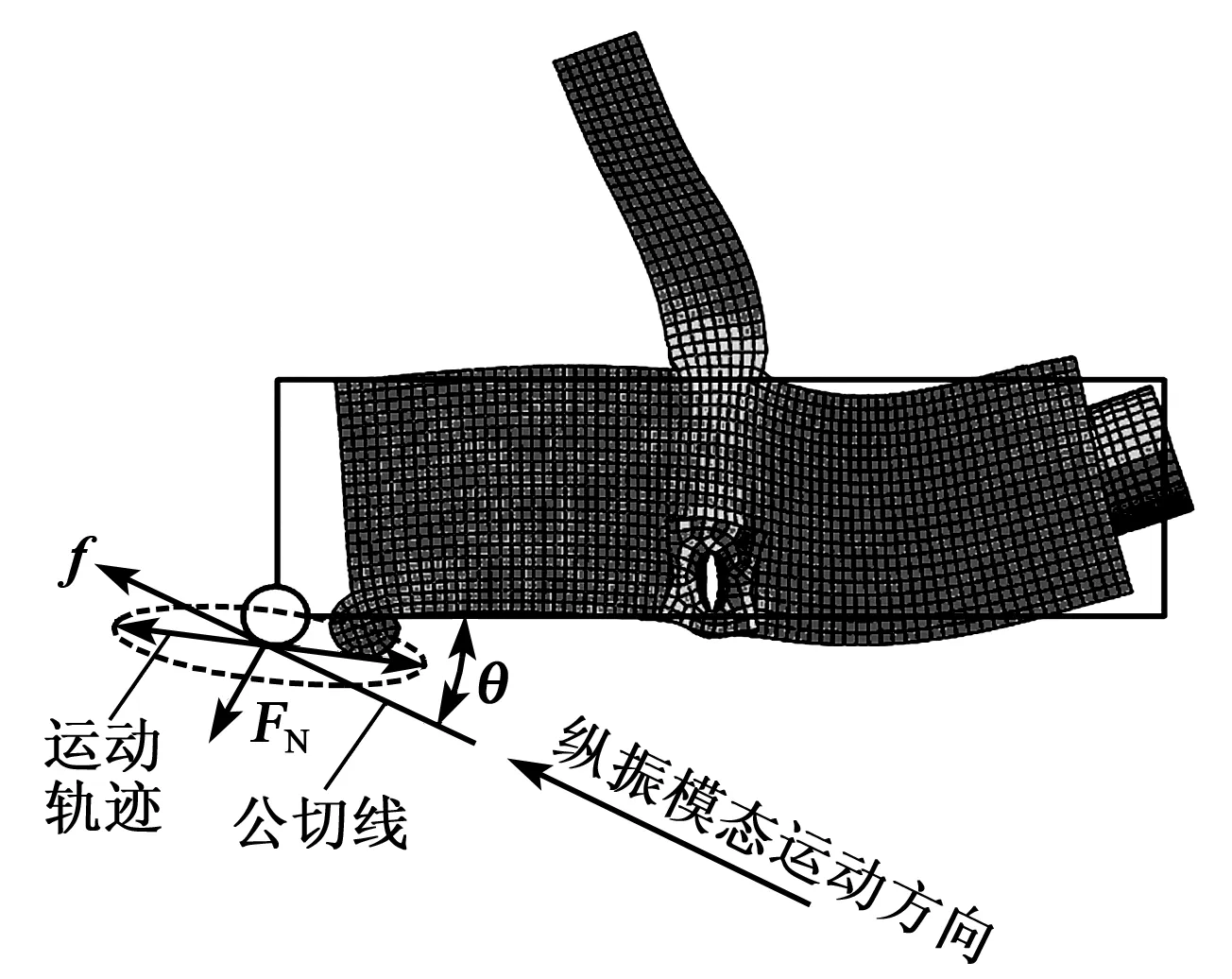
图8 纵振模态时驱动足的轨迹

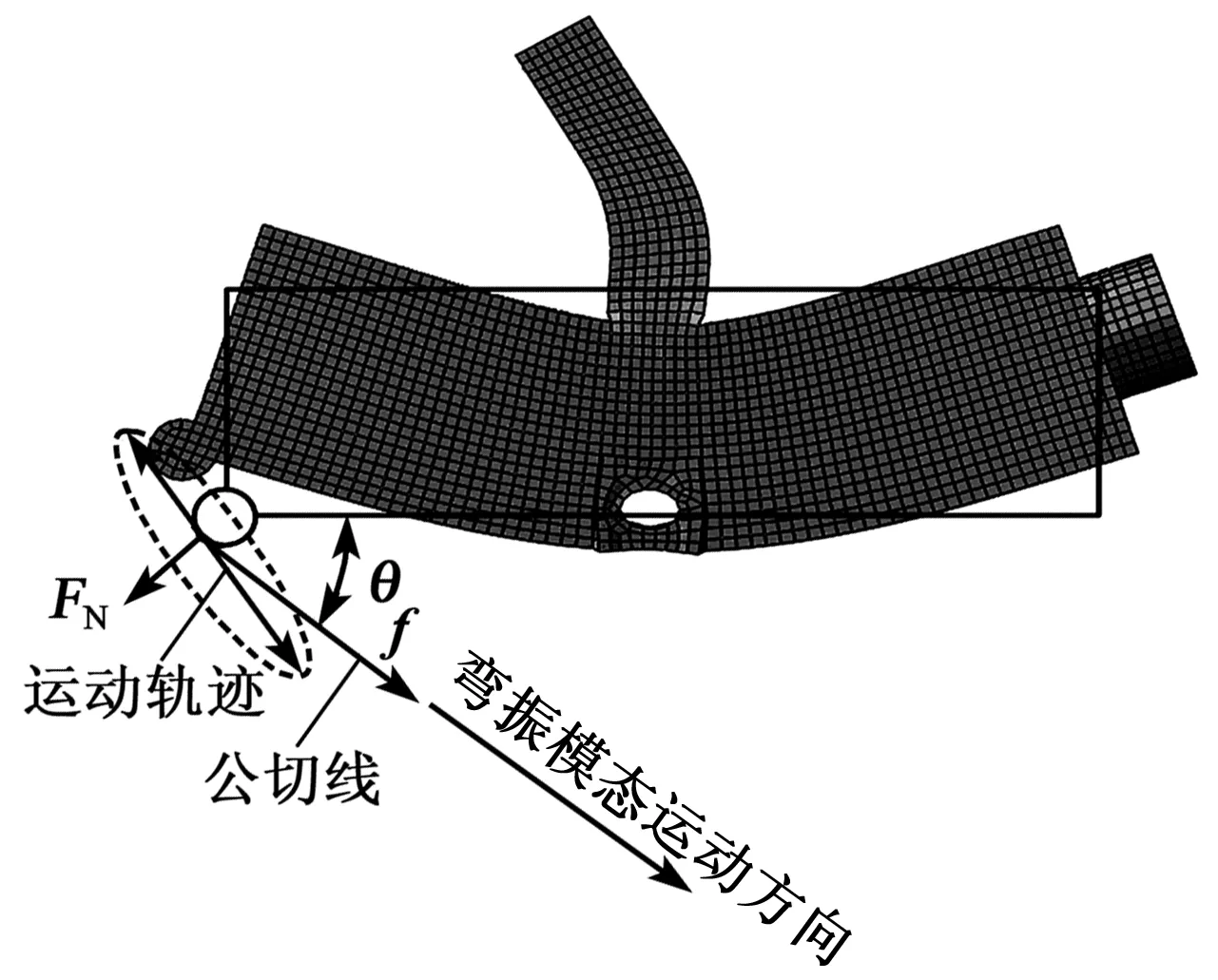
图9 弯振模态时驱动足的轨迹

4 实验

4.1 电机性能测试平台

笔者制造了多台超声电机的原型机，质量为25 g，其实物外形尺寸如图10所示。电机性能测试装置如图11所示。双通道示波器产生的两路相位差相差一定角度的正弦波电信号，功率放大器将两路正弦信号放大并施加于定子的电极，激励定子振动，定子驱动足在摩擦力的作用下推动转轴旋转。该测试台通过磁粉制动器对电机施加恒定反向扭矩载荷，并通过扭矩传感仪实时对外输出当前扭矩信号。通过光电编码器实时对外输出转动的角度信息，从而计算出电机转动角速度。一阶弯振模态工作时两路正弦波电信号相位差为0°，一阶纵振模态工作时两路正弦波电信号相位差为180°。

图10 超声电机外形尺寸

图11 超声电机性能测试平台

4.2 超声电机定子端面扫频

直线线型超声电机自身存在大量接触问题，锁紧螺栓的预紧力对工作频率的改变等非线性问题加大了有限元计算的误差。因此，在超声电机进行性能试验前，使用多普勒激光测振仪测量实际加工组装完成的定子很有必要。图12为定子端面一阶弯振、纵振模态的振动情况。

图12 多普勒激光振动模态测量

4.3 超声电机性能

实验设计了不同大小的锁紧螺栓，并加工了与其对应的定子结构，图13为不同螺栓对超声电机性能的影响(其中M4螺栓因为预压力过大导致压电陶瓷特别易碎裂而未能测得有效数据)。激励电信号峰-峰值为300 V，定子螺纹孔深度为6 mm，安装角度θ为30°。与选用M2螺栓的超声电机相比，在同等预压力下，选用M3螺栓的超声电机的扭矩提高了55%。为进一步优化电机性能，实验研究了超声电机的驱动足端螺纹孔咬合深度对超声电机性能的影响。

图13 不同螺栓对超声电机性能的影响

图14 螺纹孔深度对超声电机的影响

通过加大定子驱动足端的螺纹孔深，图14为在定子驱动足端通孔的情况下，电机比在同等预压力下，螺纹孔深为6 mm的扭矩提高了60%。图15为在空载状态下，预压力与角速度之间的关系。在θ=30°，纵振模态下，角速度随着预压力的增大先增大后减小。在预压力为15 N时最大角速度为12.63 rad/s;弯振模态下，角速度随着预压力的增大先增大后减小，在预压力为10 N时最大弯振模态角速度为54.35 rad/s。

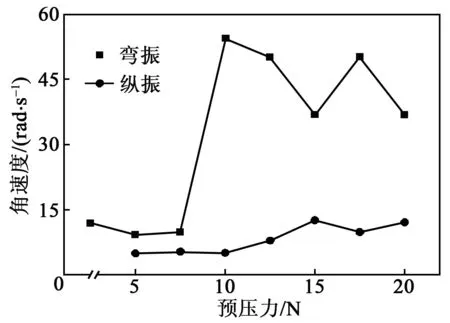
图15 空载下预压力与角速度的关系

图16为空载下定子的θ与转轴角速度的关系。预压力为10 N，弯振模态与纵振模态下角速度均随角度增大先增大后减小，最大角速度发生在定子安装角度为30°处。图17为角速度和输出扭矩的关系。θ=30°，预压力为20 N，弯振模态下，角速度随着输出扭矩增加而减少，最大输出扭矩为0.04 N·m；纵振模态下角速度亦随着输出扭矩增加而减少，最大输出扭矩为0.04 N·m。图18为激励电压与角速度的关系。超声电机的角速度随着激励电压的增大而增加。

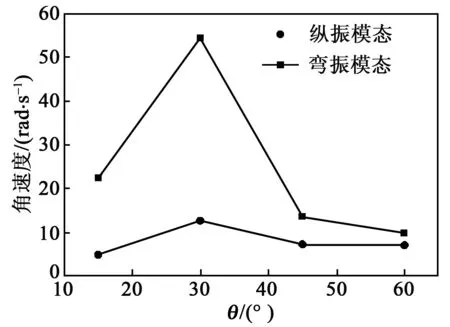
图16 空载下θ与角速度的关系

图17 角速度与输出扭矩的关系

图18 激励电压与电机角速度的关系

5 结束语

本文介绍了一种用于控制力矩陀螺的超声电机，该作动器使用两个不同的振动模态以实现对力矩陀螺框架的正、反向旋转。通过有限元分析并实际制造了原型机，该超声电机质量为25 g，弯振模态下最大角速度为54.35 rad/s，最大输出扭矩为0.04 N·m，纵振模态下最大角速度为12.63 rad/s，最大输出扭矩为0.04 N·m。满足旋转力矩陀螺的设计目标0.1 N·m的要求。