超声自行走精密定位机构

李 闻 钰

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

随着当前精密工程技术在若干领域的快速发展，对精密定位技术的需求日益增长，它要求系统具有微纳米级的定位精度[1-3]。在超声自行走精密定位机构的应用领域中，压电陶瓷微位移驱动器是近年来发展起来的新型微位移器件，它具有体积小，响应快，无噪声的特点，在微纳米级的精密定位系统中得到大量的应用[4-7]。本文提出了一种以压电陶瓷为驱动器的新型超声自行走机构，揭示了机构在自行走时的运动学特性，讨论了基于压电耦合的结构模型，基于模态分析的模态共振。实验证明该自行走机构的输出位移精度可达10 μm，若将该自行走机构应用于精密测量领域，结合控制反馈系统，可使测量系统具有稳定性强，高效准确，可靠性高，推广性好等特点。

1 结构特征及工作原理

1.1 结构设计

本文设计的结构如图1所示，该结构分为两部分：

1) 主体部分为航空铝一体结构，考虑到机构的微型化与轻量化，采用铝结构可使机构在行走过程中减少阻力，进而提高可控性。

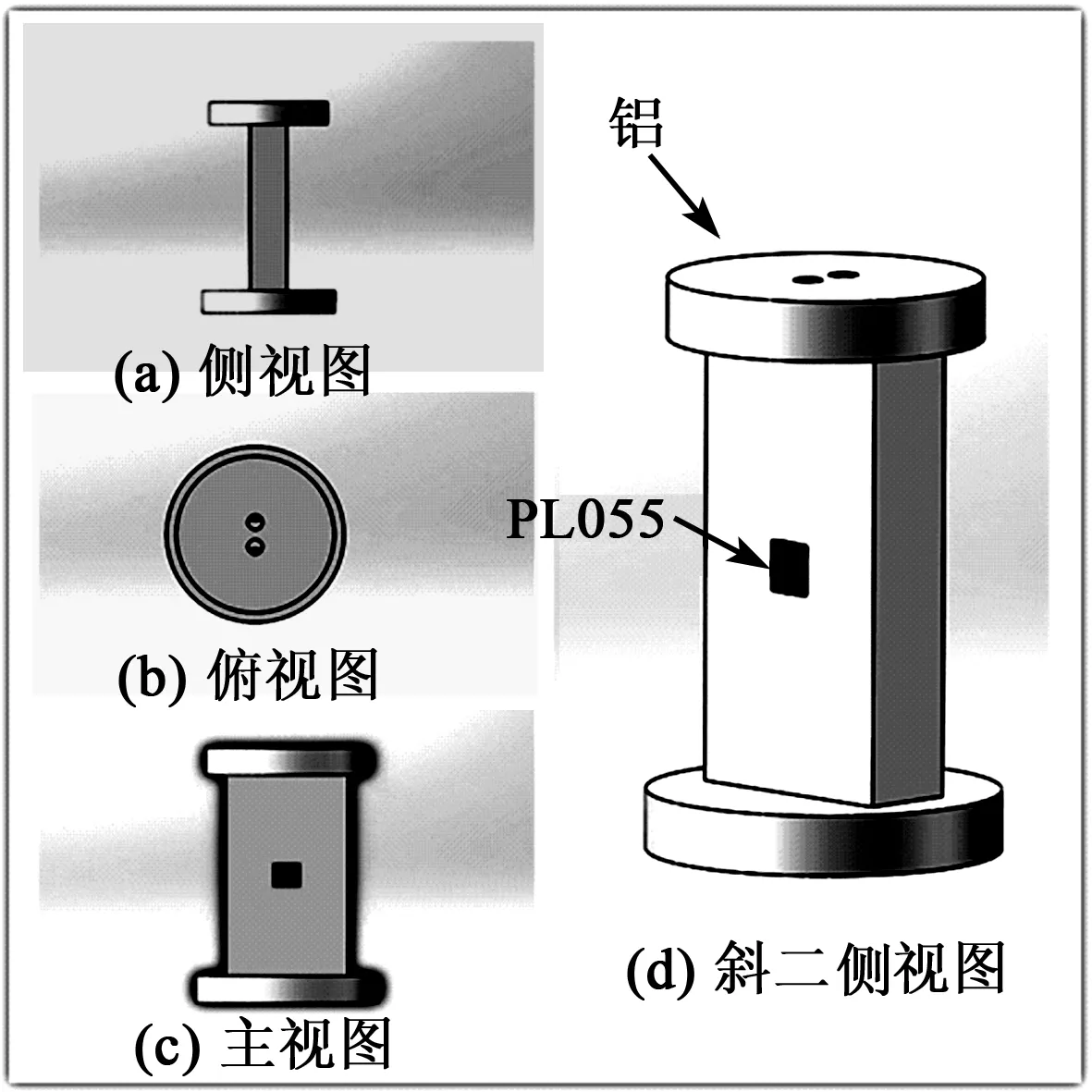
图1 机械结构模型图

2) 另一部分是压电陶瓷，主体结构的上方打有2个贯穿至腹板处的正方形孔，用来在顶丝预紧腹板处放置2个压电陶瓷。2个压电陶瓷放于腹板外侧，在易拆卸的同时也使整个结构处于对称状态。以此使设计的结构紧凑，并为模态分析创造了便利条件，利于寻找为实现其运动所需的伸长、弯曲与扭转模态。

1.2 运动原理

该结构通过压电激励使该结构伸长模态与弯曲模态超声共振来实现沿一个方向的自行走。该结构在具有伸长模态和弯曲模态的同时还具有扭转模态，通过不断的尺寸调整进行结构优化，使3种模态的频率相近，再用3种模态的共振频率去激励结构，使其发生耦合共振振动。3种模态的叠加，可以通过用适当的激励信号激发结构来实现，使该结构在沿一个方向运动同时进行反向从而沿着相反方向运动。

2 机电耦合仿真分析

2.1 仿真条件

为找到该结构的模态，需对该结构进行模态分析。为得到较精确的模态分析结果，对结构进行尺寸为2 mm的网格划分。当利用ANSYS Workbench对含有压电陶瓷的材料进行模态分析时，压电陶瓷PL055的密度为7 700 kg/m2,介电常数ε11=3 300 F/m, 弹性刚度常数矩阵及压电常数矩阵分别为

(1)

(2)

Al的密度为2 900 kg/m2,弹性模量为7.1×109Pa,泊松比为0.33。

2.2 仿真结果与讨论

为保证实现超声共振，结合实验室现有条件，需调整3种模态频率为20～40 kHz，并通过不断的尺寸优化使3种模态频率相近，且共振效果最佳。仿真所得模态如图2所示。3种模态频率相近基本符合条件，下面将进行实验找出使3种模态的共振频率，并验证机构自行走的可行性。

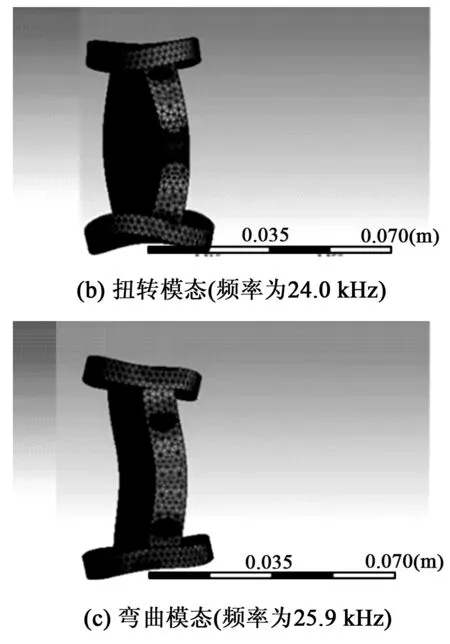
图2 模态分析结果图

3 实验结果与讨论

3.1 实验系统的搭建

本次实验是在光学防振平台上完成的，使用型号NES-200-24的明纬开关电源对功率放大器(型号E-617 LVPZT)进行供电，将控制信号输入到压电驱动上，在输出端产生的运动通过电容式位移传感器(带有探头5503的Microsense5810模块，USA)来捕获，测量的范围和带宽分别为500 μm和20 kHz，位移以电压信号的形式传送到具有D/A和A/D的数据采集板(NI PCI-6259,USA)，经由数据采集卡存储到电脑上，在开环状态下进行测试实验。在反馈控制方面，设计的控制算法通过桌面实时环境中Matlab/Simulink模块实现，具体流程图如图3所示。加工出的实物图如图4所示。

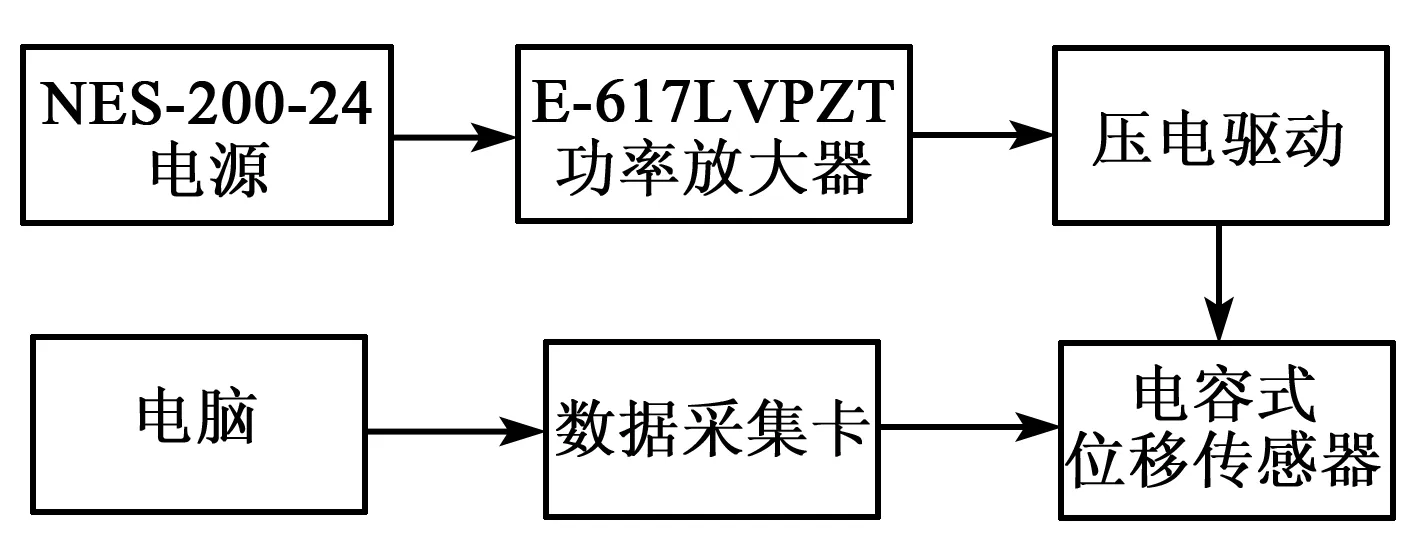
图3 参数辨识测试系统流程图

图4 加工实物图

3.2 激励频率响应特征

由图2可知,该结构的3种模态及其对应的频率为找到共振频率，考虑到理论模型与实际存在的误差，现通过两个压电陶瓷分别输入相同的频率，在20～28 kHz,以500 Hz为单位分为17组进行实验，计算并比较得到的位移值。当找到实现行走时位移最大的频率，该频率即为伸长模态与弯曲模态共振的最优频率。将数据采集卡采集到的数据整理成机构位移-运行时间曲线图与位移-频率图，如图5所示。

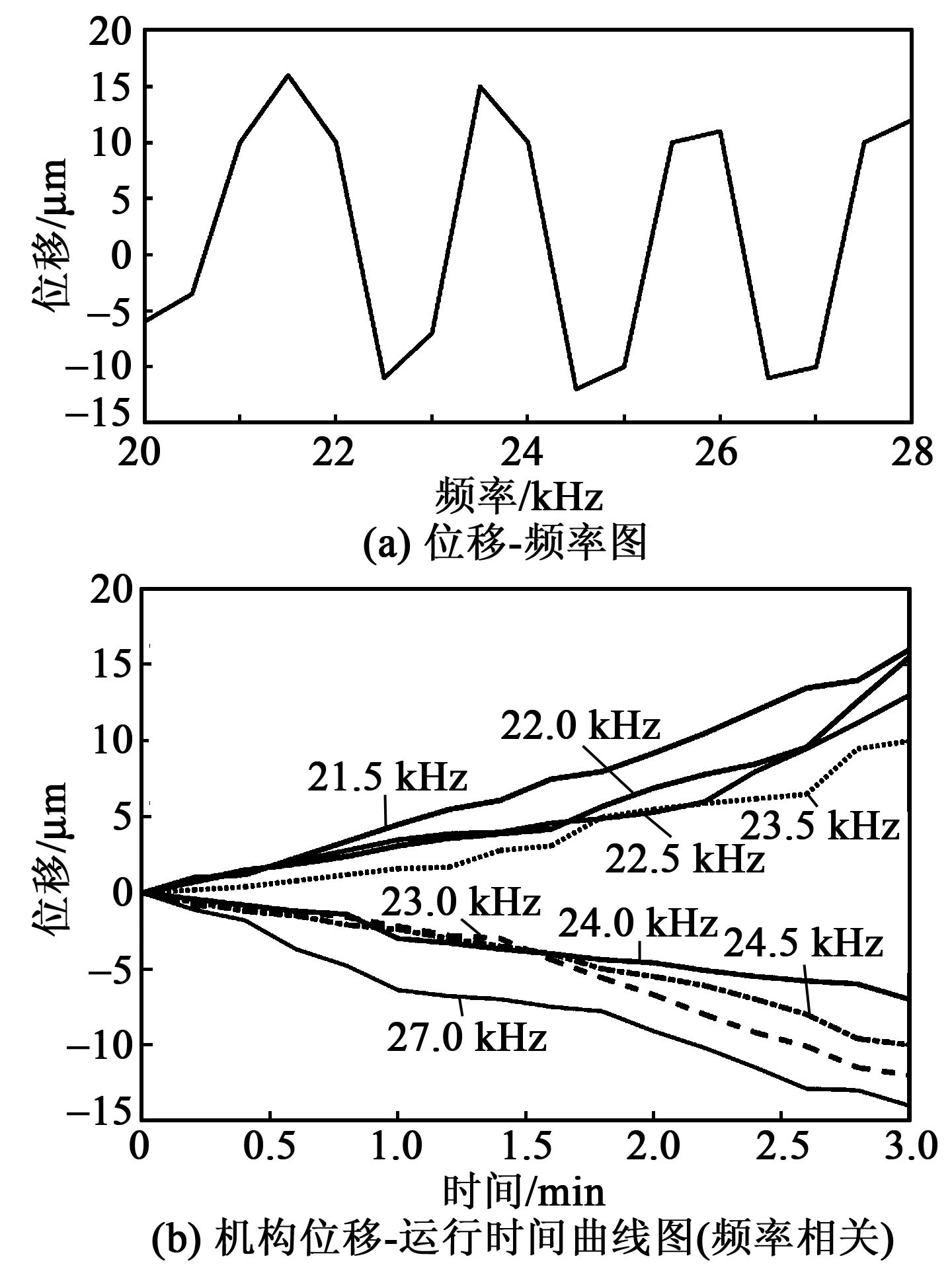
图5 激励频率响应特征图

由图5可知，最大位移16 μm出现在频率为21.5 kHz处，计算出最大速度为8.8×10-2μm/s，该频率即为最优共振频率。同时，由图还可知位移存在反向，说明在基于伸长模态与弯曲模态共振实现自行走的基础上，加上扭转模态共振后使物体呈现反向运动。为进一步实现反向运动控制，需要在21.5 kHz频率条件下调整两输入频率的相位，来找到实现反向的情况。

3.3 反向运动控制

在21.5 kHz输入频率条件下调整两输入频率的相位差(Δφ)，Δφ在0～π时分6组进行测试，同样，将数据采集卡采集到的位移曲线汇总至同一起点，整理成机构位移-运行时间曲线图如图6所示。

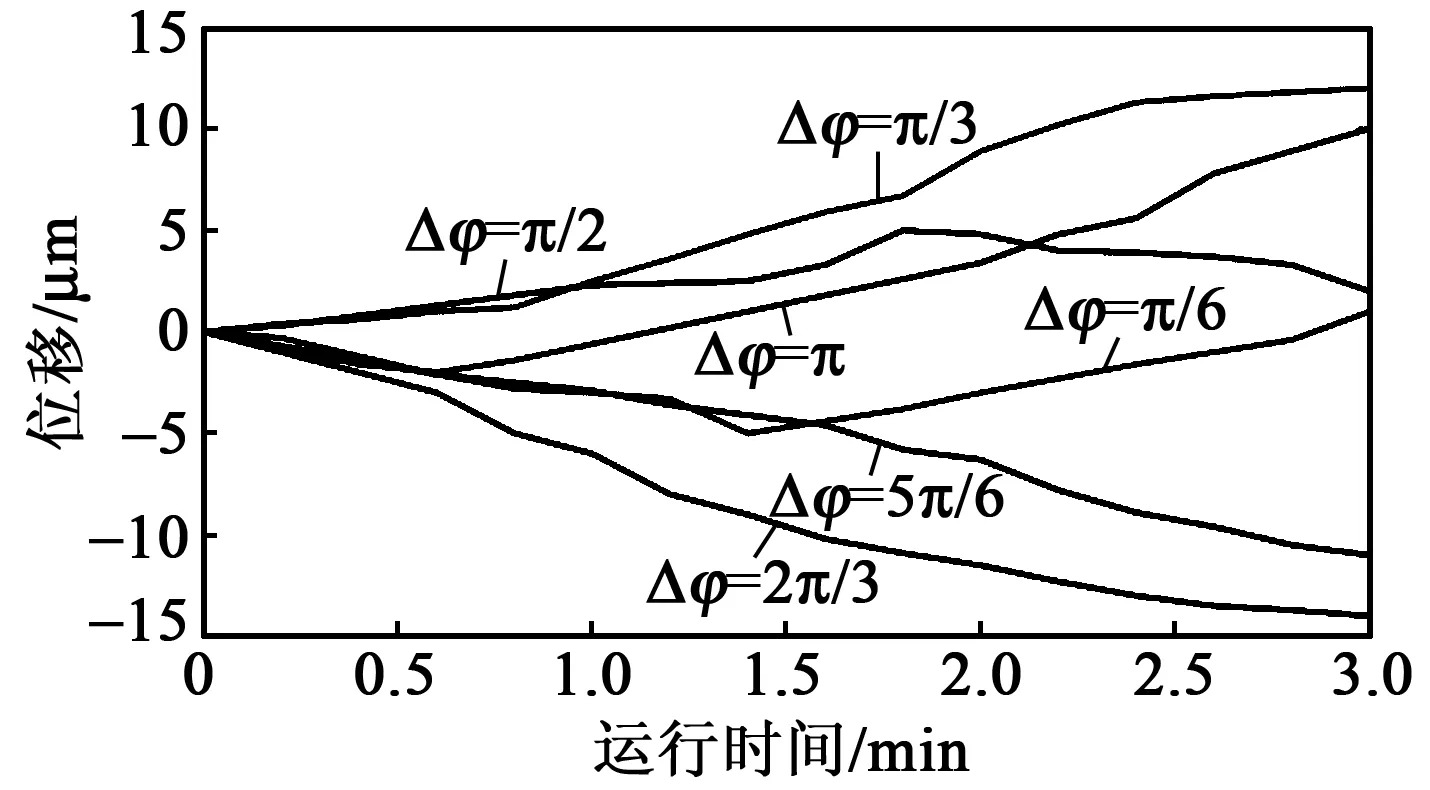
图6 机构位移-运行时间曲线图(Δφ相关)

由图6可知，当Δφ为π/6、π/2、π时机构在沿一个方向运动的同时也进行反向运动。由此，便实现了机构沿一个方向实现自行走并进行反向运动的可控性。

3.4 激励电压响应特征

为进一步优化机构自行走的性能，在输入频率的幅值上进行调整，考虑到压电陶瓷的限定电压范围，其他条件不变，输入频率幅值在10～50 V时分5组进行测试，得到位移-输入电压幅值曲线如图7所示。

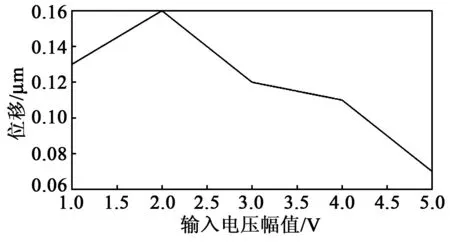
图7 位移-输入电压幅值曲线图

由图7可知，当输入电压幅值为20 V时，机构位移达到最大，且在达到最大位移后，随着输入电压幅值的增加，机构的自行走位移有下降趋势。由此可知，输入电压幅值是影响机构自行走的一个重要因素，为使运动效果最佳，需要对输入电压幅值进行必要的调整。

4 结束语

本文根据现代压电驱动器高效，低能耗，响应快的要求，提出了一种可自行走的微型机器设计方法，并介绍了微型机器的结构和工作原理。然后研究了仿真中的模态分析及验证实物性能的实验测试。最后，给出了在机构的3种模态共振下如何提高微型机器自行走性能的方法。实验结果证明，微型机器的运动测量精度在微米级；在21.5 kHz激励下，自行走运动最大速度为8.8×10-2μm/s；当两输入频率相位差为π/6、π/2、π时便可实现在沿一个方向运动的同时进行反向运动，基本满足了超声自行走微型智能机器的要求。