双圈图的Seidel无符号拉普拉斯能量
周后卿
(邵阳学院 理学院,湖南 邵阳,422000)

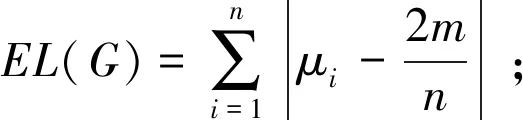

2017年,RAMANE H S等[13]介绍了Seidel 拉普拉斯矩阵的性质和Seidel拉普拉斯能量。定义图G的Seidel 拉普拉斯矩阵为SL(G)=DS(G)-S(G),其中,DS(G)是一个对角矩阵,DS(G)=diag(n-1-2d1,n-1-2d2,,n-1-2dn)。


本文研究双圈图的Seidel无符号拉普拉斯能量问题。
1 几个引理
首先回顾一下图的邻接矩阵,拉普拉斯矩阵,Seidel矩阵的特征值之间的关系。
对于Seidel无符号拉普拉斯矩阵特征值,由代数学知识可知,矩阵的迹(trace)等于矩阵的特征值之和,即
(n-1)(n2-8m)+4Z1(G)。
若G是一个具有顶点n的简单连通图,其边数为n+1,则称G为双圈图。
下面给出几个引理。
引理1[13]设G=(V,E)是一个具有n个顶点,m条边的简单图,则
引理2[15]设Βn,k表示一类具有顶点n、悬挂点k的双圈图集合,若G∈Βn,k且0≤k≤n-5,则Z1(G)≤4n+k2+5k+12 。
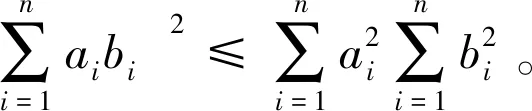

2 主要结论
现在证明本文的几个结论。
定理1 设G是具有顶点n、悬挂点k的双圈图,且0≤k≤n-5,则
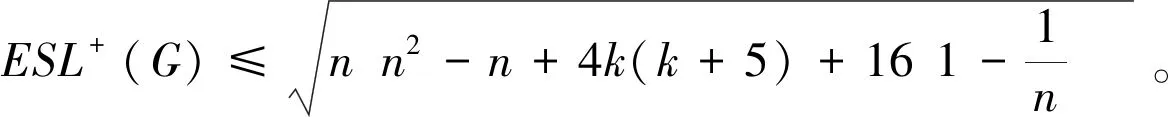

现在用一个例子来验证一下定理1的准确性。如图1所示,G是一个具有8个顶点、3个悬挂点的双圈图,这里,n=8,k=3,根据定理1计算 ,有ESL+(G)<36.441 7。借助于计算软件mathematica,可以直接求出双圈图G的Seidel无符号拉普拉斯矩阵SL+(G)的特征值为9.665 29,4,4,4,4,1.778 98,0,-7.444 28。再根据Seidel无符号拉普拉斯能量定义可求出其能量为ESL+(G)=26.331 829。显然有26.331 829<36.441 7,说明定理1成立。
证明 由于G是双圈图,所以,边数m=n+1。在引理3中,令bi=1,
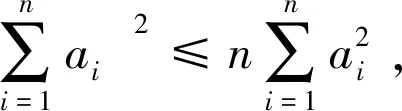
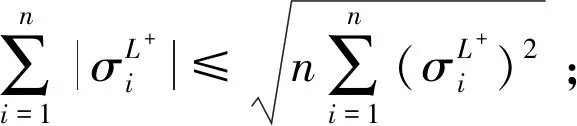
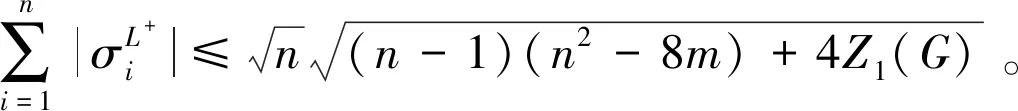
因此,对于双圈图G的Seidel无符号拉普拉斯能量
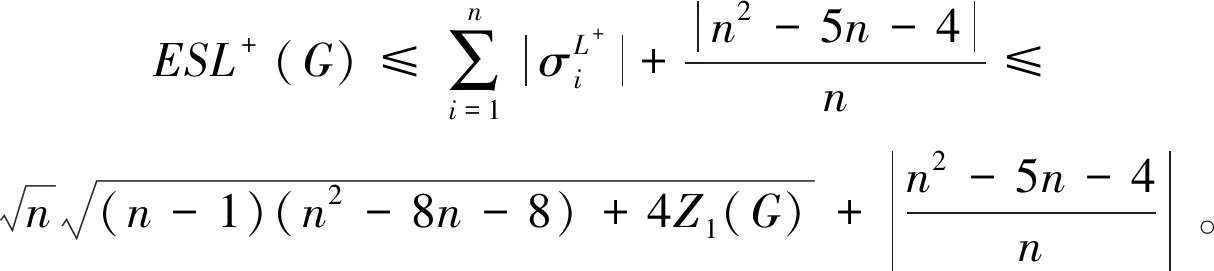
同样以上述例子为例,验证定理2的准确性。这里,G的第一类Zagreb指标Z1(G)=68。
根据定理2计算有ESL+(G)≤44.069。显然26.331 829≤44.069,即定理2成立。
定理3 设G是具有顶点n的双圈图,若G的Seidel无符号拉普拉斯矩阵的Frobenius范数‖SL+(G)‖F已知。则G的Seidel无符号拉普拉斯能量满足下列不等式
证明 由Seidel无符号拉普拉斯能量定义可知,
因为G是双圈图,结合引理4,由上式可推出
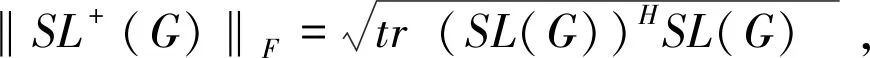
从上述例子来看,定理1中的界比定理2中的要优,而定理2中的界比定理3中的更精确一些。

