基于可接受调整量水平的航班时刻优化研究*

汪梦蝶 胡明华 赵 征

(南京航空航天大学国家空管飞行流量管理技术重点实验室 南京 210016)

0 引 言

20世纪80年代,国内外学者开始研究和开发地面等待策略，而后将成果拓展至了航班时刻优化领域.Zografos等[1]通过制定符合欧盟规范和IATA时隙分配指南的模型来解决单机场的战略阶段航班优化问题，并应用于三个希腊机场的实际数据.结果表明,航班调整总量在14%～95%的范围内降低.Castelli等[2]建立了考虑航班起降时刻和相应航线的多机场网络优化模型.Pyrgiotis等[3]设计了考虑联程航班限制的整数规划两阶段模型，旨在求出一个最小化航班调整量的时刻表，同时将总体调整量保持在尽可能低的水平，以提高单机场容量利用率.Jacquillat等[4]提出了结合容量动态规划模型和航班延误排队模型的单机场航班时刻综合调配方法，从而联合优化战略阶段的航班时刻表和战术阶段的容量利用策略.胡明华等[5]基于多元受限地面等待策略建立了多元受限航班时刻优化模型，并提出改进启发式算法.彭瑛等[6]分析了航班时刻编排对跑道延误的影响，建立了平均跑道延误时间最少、总时间片调整最少、总延误航班架次最少的多目标航班时刻优化排序模型.曾奇[7]在传统航班时刻优化模型上改进了三种给予补偿机制的模型，采用Xpress-MP建模和优化工具进行求解.王湛等[8]以协同决策理论为基础，在降低延误时间的前提下优化了进场航班，提高了机场之间时空资源使用的公平性.王倩等[9]在满足延误水平的基础上，从航空公司公平性的角度构建了模型，并设计了基于粒子群算法的布谷鸟搜索算法.

综上，目前航班时刻优化的相关研究主要集中在以航班调整总量、最大航班调整量、航班延误时间等函数的组合作为优化目标的多元受限模型，并没有考虑航班可接受调整量水平，也没有针对时刻表功效性和可接受性之间关系的研究,因此，本文旨在分析优化过程对功效性和可接受性的影响，使配置结果更加符合现实运行需求，从而真正提高资源使用效率.

1 航班时刻优化的功效性与可接受性分析

我国航班时刻管理遵循以政府为主导的行政配置模式，这可能会导致调整后的航班时刻所在的时段不够吸引航空公司进行实际运行，从而出现航空公司空置、虚占航班时刻或者售票时刻与批复时刻不一致的情况，见表1.这类情况的根源配置过程中没有预先考虑实际运行航班时刻表的可接受性.

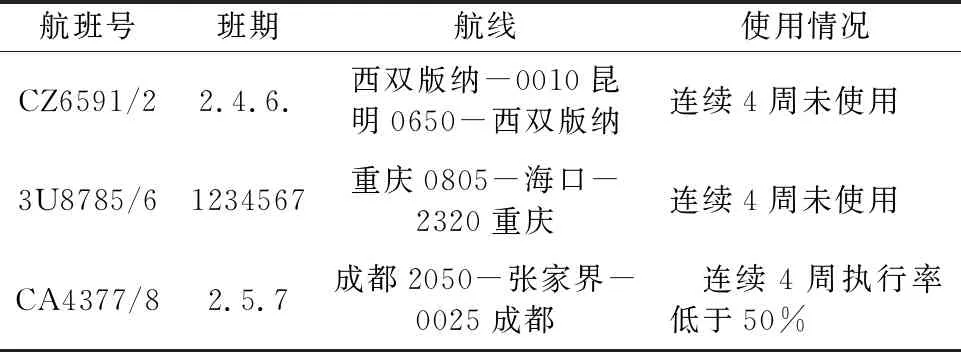
表1 西南地区2011/2012年冬春季繁忙机场航班时刻监管通报部分内容

因此，文中提出航班时刻表可接受调整量水平的概念，在模型中用可接受调整量表示，并将超过可接受调整量的航班数量作为目标函数之一，定量分析时刻表的可接受性，作为航空公司对航班时刻优化结果满意程度的度量；航班时刻优化的功效性则用航班调整总量来表示，从而构建以配置效率和可接受度为双目标的优化模型，研究二者之间的关系，力图从根源上减少航空公司取消或不执行分配的航班时刻的情况，增加繁忙机场稀缺容量资源的利用率和航班执行率.

假设六个航班r1～r6必须配置在时间片1～15，r1～r3申请的时间片为7，r4-r6申请的时间片为10，每个航班的可接受调整量为±2个时间片，容量约束是每三个时间片二个航班，暂不考虑周转时间限制.

表2为仅优化航班调整总量的情况.灰色阴影表示航空公司申请的时间片，而优化后分配的时间片用“#”表示.表3为考虑优化航班调整总量和超过可接受调整量的航班数量的情况.由表2～3可知，为将超过可接受调整量的航班数量减少一个，航班调整总量将增加一个时间片.即由于航班r6向左移动一个时间片，需要将航班r1和r4分别向左移动一个时间片，以满足容量限制.

如果减少超过可接受调整量的航班数量，则所有航班的调整量将更均匀地分布，航班调整总量可能增加，即二者是互相矛盾的优化目标，因此需要寻找适当的模型和算法来探究二者之间的权衡关系.

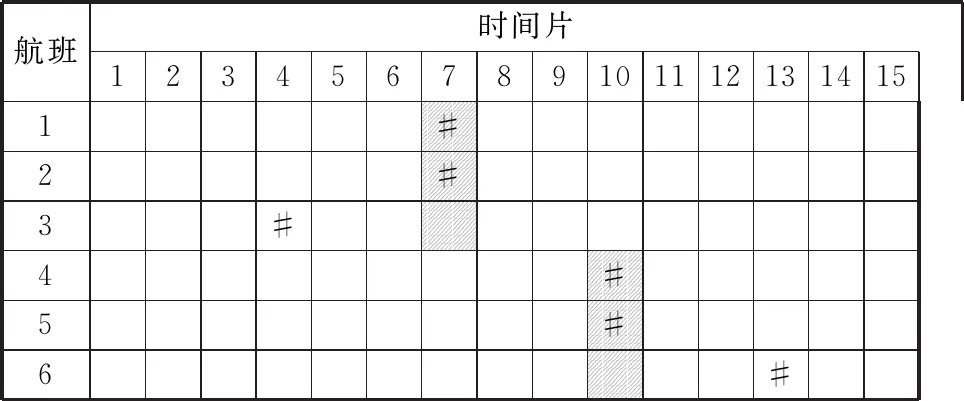
表2 优化航班调整总量

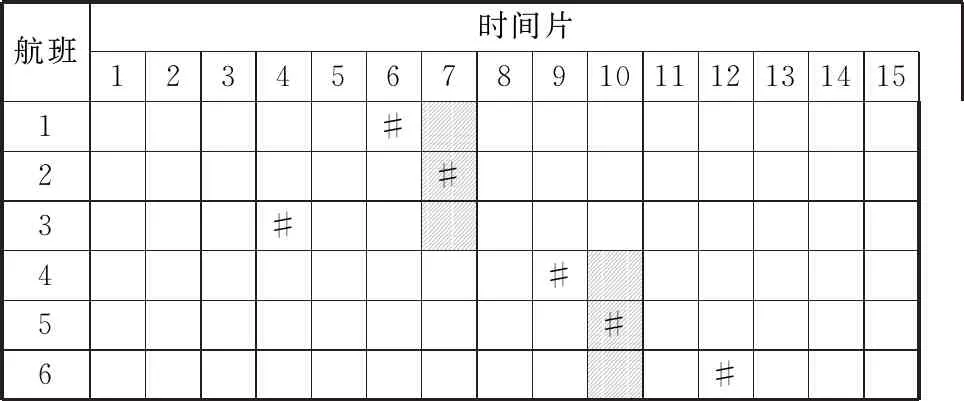
表3 优化航班调整总量和超过可接受调整量的航班数量

2 航班时刻优化模型

2.1 参量定义

决策变量：

式中：r∈R,t∈T.

附加变量：

式中：r∈R.

2.2 目标函数

1) 通过最小化航班调整总量实现要求配置达到整体最优性的功效性目标.

(1)

2) 通过最小化超过可接受调整量的航班数量实现要求航空公司对优化结果满意的可接受性目标.

(2)

2.3 约束条件

1) 每个航班只能分配一个时间片.

(3)

2) 滚动进场/离场/总容量约束.

(4)

(5)

(6)

式中：Δt∈{1,3,12}，Ts={t∈T|s≤t≤s+Δt}，s∈[0,n-Δt+1).

在模型中若只对机场小时容量进行限制，会导致某些时段的时间片航班过于密集.为了让模型更精细化，本文将分别对时间区间长度为5，15和 60 min的进场、离场和总容量进行限制.此外，由于滚动小时容量约束是对每个开始于前一个约束5 min之后的小时容量进行限制，从而滚动遍及整个优化时间段，因此相比于常见的以自然小时划分的容量约束，它可以确保容量饱和的情况在一天内不会持续很长时间，从而允许在运行高峰期间进行系统恢复.

3) 联程航班的最小过站时间约束.

(ra,rd)∈P，k∈[tad,n)

(7)

以下约束用于定义超过可接受调整量的航班数量(yr).

4) 统计分配给航班r的时间片超过可接受航班调整量的情况.

如果分配的时间片小于下限τr-qr，则yr=1.

(8)

如果分配的时间片大于上限τr+qr，则yr=1.

(9)

5) 统计分配给航班r的时间片未超过可接受航班调整量的情况.

如果分配的时间片小于上限τr+qr，则wr=0.

(10)

如果分配的时间片大于下限τr-qr，则vr=0.

(11)

6) 用wr和vr定义yr，如果分配的时间片未超过上下限，则yr=0，即分配的时间片位于可接受范围内.反之，如果wr或vr中的一个值为1，则航班r被定义为超过可接受调整量的航班.

yr≤wr+vr，r∈R

(12)

3 基于ε-约束法和改进粒子群算法的模型求解

3.1 基于ε-约束法的优化模型

根据上述目标函数及约束条件，航班时刻优化配置模型为

s.t.

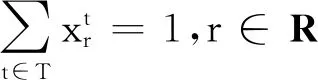
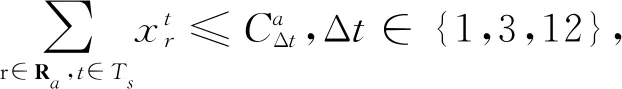
Ts={t∈T|s≤t≤s+Δt},

s∈[0,n-Δt+1)

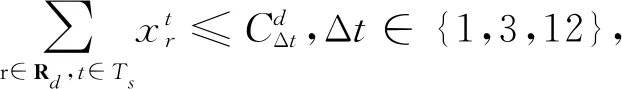
Ts={t∈T|s≤t≤s+Δt},

s∈[0,n-Δt+1)

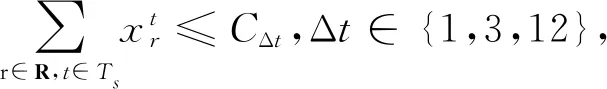
Ts={t∈T|s≤t≤s+Δt},

s∈[0,n-Δt+1)

(ra,rd)∈P,k∈[tad,n)

yr≤wr+vr,r∈R

(13)

采用近似有效边界方法之一的ε-约束法来求解这个双目标0-1整数规划问题.与其他方法相比，ε-约束法能在无需额外参数的情况下高效得到Pareto解集，其原理是依次对多目标问题的每个目标进行求解，将求出的最优解作为约束条件增加在原模型中，其模型为

minfh(X)

(14)

fi(X)≤εi，1≤i≤k，i≠h

(15)

X∈Xf

(16)

式中：fi(X)为第i个目标函数；εi为第i个目标函数fi(X)的上界.

因此，根据ε-约束法将双目标航班时刻优化问题转化为单目标优化问题，步骤如下.

步骤1利用目标函数(1)和约束(3)～(12)，建立模型1并求解，其最优解为航班调整总量的最小值(z1)min.

步骤2利用目标函数(2)和约束(3)～(12)，建立模型2并求解，其最优解为超过可接受调整量的航班数量的最小值(z2)min.

步骤3利用目标函数(1)和约束(3)～(12)加上(17)，建立具有新参数ε的模型3，约束(17)如下所示.

(17)

式中：ε从模型2中确定的(z2)min开始，每次增加一个单位，迭代求解一系列z1值，直到其等于(z1)min为止该方法的优点在于可以得到两个目标函数寻优过程中的一系列数值，从而便于比较两个目标函数在不同可接受调整量水平下的所有可能值的变化趋势.

3.2 改进粒子群算法

粒子群算法收敛快，具有很强的通用性，但同时存在容易早熟收敛、后期迭代效率不高等缺点.而本文采用的改进粒子群算法，借鉴遗传算法中的变异思想，引入变异操作，从而拓展在迭代中不断缩小的种群搜索空间，使粒子跳出先前搜索到的最优值位置，从而提高找到更优值的可能性.算法流程见图1.

图1 航班时刻优化算法流程图

4 模型应用和结果

选取南京禄口国际机场2017-08-18的航班时刻，期间共起降航班621架次.应用matlab7.0软件编写并运用上述ε-约束法和改进粒子群算法，取N为100，kmax为300，c1、c2取2.0，pm取0.1，惯性权重区间[0.4,0.9]，粒子速度区间[-5,5].其中容量分别为38架次/h，10架次/15 min，4架次/5 min，联程航班的最小过站时间为60 min.为分析可接受调整量水平对优化目标的影响，分别取q的值为3，6，9，12对模型进行求解.

图2为不同可接受调整量水平对应的航班调整总量z1和超过可接受调整量的航班数量z2的值.

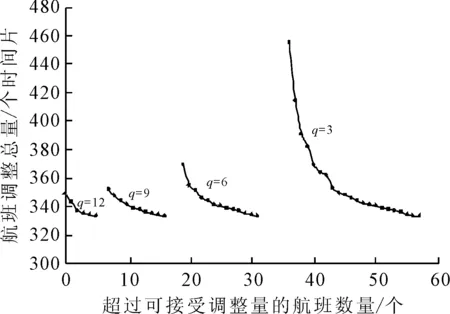
图2 不同可接受调整量水平对比图

由图2可知，这两个优化目标之间的权衡关系.当q=3时，z1增加9%(从369～333个时间片)使z2减少了30%(从57～40个).而当q分别为6，9，12时，z1只需要增加不超过5%，z2就可以减少达到30%.即说明通过航班调整总量非常小的牺牲，可以实现超过可接受调整量的航班数量的显著优化.而这个临界点则可以为航空公司设定可接受调整量水平提供参考.此外，因为航空公司申请的和最终配置的航班时刻之间的时间差明显缩小，会激发他们研究并制定出更贴合实际需求的航班时刻.

另一方面，当q=3时，z2减少35%(从57～37个)使z1增加20%(从414～333个时间片).对于q为6、9的情况，z2减少35%会使z1分别仅提高不到6%、2%；而如果q为12，该值则不到1%.这说明z1随z2的减小而增加的变化率随着q的逐渐增加而减小.由此可以推论出，航空公司对可接受调整量水平的阈值越严格，由航班调整总量代表的成本就越高.这一发现可以提醒航空公司，如果虚占航班时刻或者通过其他行为变相提高可接受调整量水平，那么对于整个机场的所有用户群而言，超过可接受调整量的航班数量和航班调整总量将会增加更多，最终损害的还是航空公司的利益.

此外，本文还选取了按照先来先服务(first come first serve, FCFS)原则以及当q=6时模型1、模型2和模型3的最优解对应的航班时刻表，应用Airtop仿真软件对禄口机场的实际运行情况构建基准仿真模型，仿真示意图见图3.

图3 南京禄口机场终端区航班流仿真示意图

输出结果见表4.由表4可知，双目标优化模型3可以兼顾功效性和可接受性准则，而模型1、模型2则顾此失彼；与FCFS方法的仿真结果相比，双目标模型3的平均延误时间减少了25%，放行正常率提高了11%.

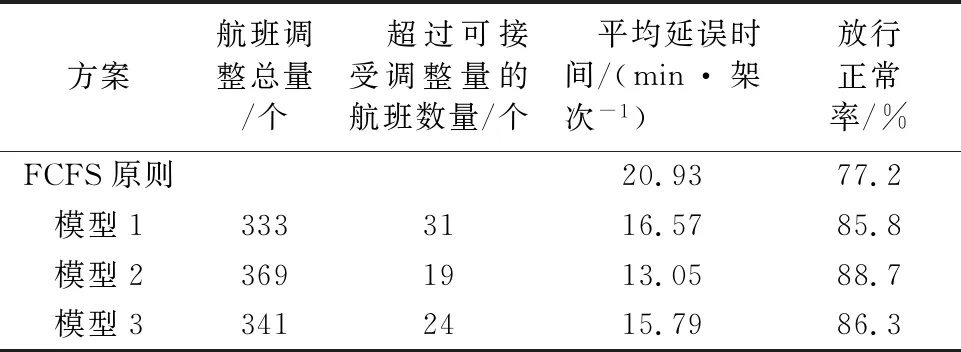
表4 Airtop仿真结果

5 结 束 语

文中提出的航班时刻优化配置策略，立足于可接受调整量水平，给出了考虑滚动容量和过站时间约束的多目标优化模型，采用ε-约束法和改进粒子群算法对模型进行了求解分析，结果表明，通过少量甚至可以忽略不计的航班调整总量的牺牲，可以从整体上让机场所有的航班时刻都更接近航空公司的需求；通过Airtop仿真验证了模型在实际运行中将使机场平均延误时间和放行正常率均得到优化.

该模型可以为机场和管制部门优化航班时刻提供决策支持，通过确定适当的可接受航班调整量水平，有利于提高机场现有资源利用率，也有利于激励航空公司对航班时刻的高执行率，从而缓解拥堵延误，提高航班正常率.在未来研究中，将结合扇区、航路等空域结构因素对区域航班时刻优化问题作进一步探讨.