基于LMT模型的特征工程分析——以泰坦尼克号为例的船舶安全管理实践

周峙泓 沈 克 范培华

(上海外国语大学 国际工商管理学院，上海 200083)

RMS Titanic沉船事件是历史上著名的灾难事件。1912年4月15日，泰坦尼克号从英国南安普敦出发，途经法国瑟堡-奥克特维尔以及爱尔兰昆士敦，驶向美国纽约。其在此处女航中与冰山相撞后沉没，2224名乘客和机组人员中有1502人丧生，事发时正是泰坦尼克号从英国南安普敦港至美国纽约港首航的第5天。该船当时是世界上最大的邮轮，1912年4月14日星期天23时40分与一座冰山擦撞前，已经收到6次海冰警告，但当瞭望员看到冰山时，该船的行驶速度正接近最高速。由于无法快速转向，该船右舷侧面遭受了一次撞击，部分船体出现缝隙，使16个水密隔舱中的5个进水。泰坦尼克号的设计仅能够承受4个水密隔舱进水，因此沉没。

通过分析幸存者名单，本文发现，虽然最终幸存有一些运气因素，但是的确有一些人比其他人更有可能幸存，比如妇女、儿童和上层阶级。是否从上船伊始，生死已定？所谓“运气”是否能够在关键时刻决定生死？是否存在某些特征因素可预测或影响乘客的存活？

因此，本文通过建立LMT模型，运用机器学习算法Weka和Python对泰坦尼克号的幸存者数据进行特征工程分析，探究乘客特征因素对幸存率的影响，以期为后世沉船事件提供船舶安全管理实践参考。

1 研究方法

1.1 数据挖掘算法

首先，通过定性分析对各属性对预测变量的影响方向和程度进行初步判定，避免由于对属性的不了解造成对数据处理时的主观臆断；同时进行初期特征工程，从难以处理的属性(Name、Ticket、Cabin)着手，初步析出属性并判定冗余变量，以便选择算法后对数据进行再次处理和调参。

随后进行定量分析，利用Pearson Correlation Heatma方法理清各属性间的相关关系，生成特征相关图，量化一个特征和另一个特征的相关程度，以进行冗余变量的剔除工作。同时，避免在模型融合的过程中，如将决策树算法与Regression算法进行融合，造成由于 multicollinearity导致的测试集准确率低。

1.2 数据挖掘过程

选择Weka-Classifier-Trees算法——Random Forest、LMT、J48、REP Tree四种算法，比较优劣。

基本思路：

(1)对数据进行分类再处理(共分六个dataset，参考之前对属性的定性及定量分析；分析办法：控制变量法)。

train_1: 本着Simplicity First原则，删去属性Name和Ticket。

train_2: Name分类原则①：按性别及年龄混合信息 [Mr.(包含Master., Jonkheer.等其他前缀), Miss.(Mlle.), Mrs. (Ms., Mme.)], (0, 1, 2); Age：取整体Mean对缺失值进行填充；Ticket：按length个数进行赋值；Fare: (0, 1-10, 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80, 80-90, 90-100, 100-200, 200-300, 300-), (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13) 对处理过的人均票价再次进行分段。

train_3: Age：分段处理(0-1, 1-9, 10-19, 20-29, 30-39, 40-49, 50-59, 60-69, 70-79, 80-89), (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)，其余属性处理方式同train_2，删去Ticket，试析该属性对模型拟合度影响；→结果：非常小，Remove属性Ticket。该结果与定性分析设想基本一致，Ticket为冗余变量，其特征工程析出属性基本涵盖在Pclass(数字首位)，Parch、SibSp(重复数值)，Embarked(字母)中。

train_4: Cabin：(A, B, C, D, E, F, G, T), (1, 2, 3, 4, 5, 6, 7, 8)(不允许缺失值，将Cabin缺失值默认设为0)，其余属性处理方式同train_3。

train_5: Name分类原则②：按性别及社会地位混合信息 [Sir.(Capt., Don., Major., Col., Sir.), Lady. (Dona., Lady., the Countess.)], (3,4,5) ；Cabin按有无数据分类，(String，null), (1, 0) ；其余属性处理方式同train_3。

train_6: Name分类原则②，Age分段，Cabin分段；其余属性处理方式同train_3。

(2)用相关算法对进行特征分析后的数据进行拟合

2 数据分析

2.1 样本数据

Titanic数据中共有两个数据集——训练集和测试集，其中训练集共有12个属性，891条样例，测试集有11个属性，418条样例。表1给出属性变量的介绍。

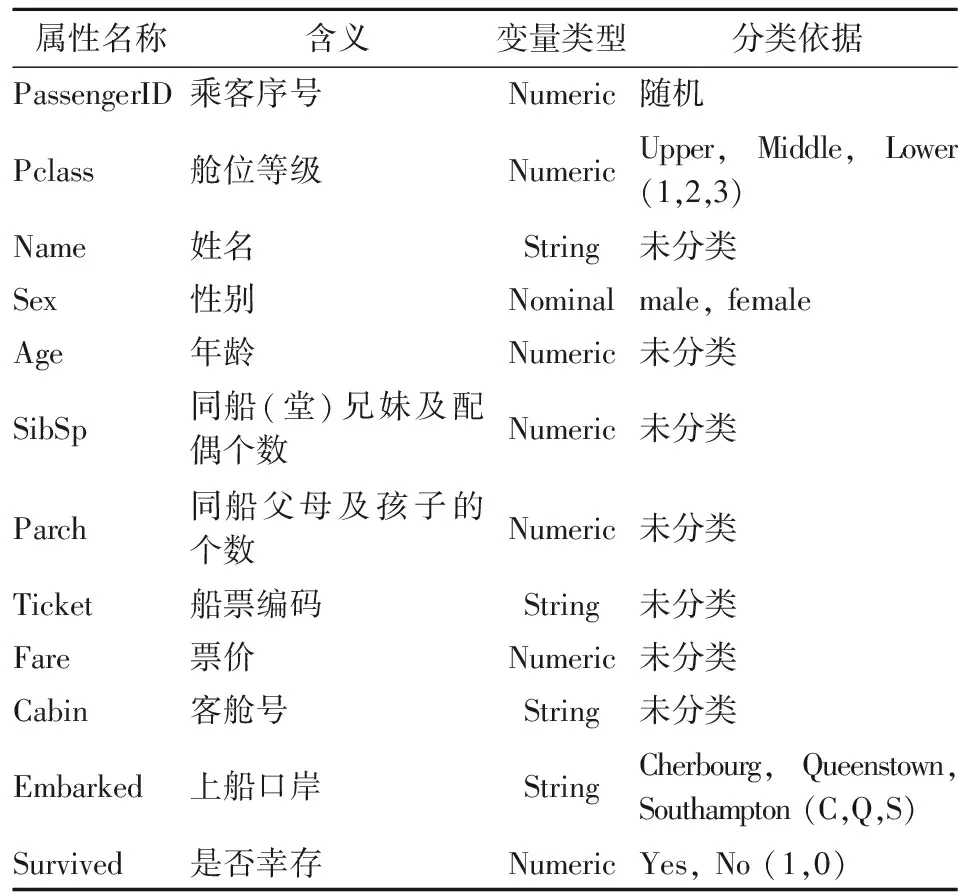
表1 属性总览

由于数据本身具有其含义，避免由于数据可能偶然的高度相关造成训练集拟合度高、测试集准确性低，即模型未抓取重要特征造成预测结果的不准确，分别对具体属性进行定性分析和定量分析。

2.2 定性分析

(1)Pclass。案例中已经将乘客的社会地位分为Upper、Middle、Lower三类，分别赋值为1、2、3。试分析属性变量社会地位。1912年Titanic建造、下水、最终分崩离析究竟是在什么时代呢？20世纪初期，第二次工业革命进行得如火如荼，资本主义经济高度发展，世界分工早已形成，社会拜金思想盛行，发展高度不平衡，贫富差距巨大。社会阶层这一属性，从金钱角度看，他们拥有更好的舱位(一等舱)，在危机到来时能够第一时刻预警逃生；从社会心理角度，逃难时，更易获得尊重的地位或者更能给出的利益可能会使得他们有更大的概率获得救生艇，得以存活。因而，Pclass应该和Survived高度相关。但需要注意的是，如需使用Linear Regression及其相关混合算法，应注意Pclass和Ticket、Fare、Cabin的相关性，避免因多重共线性造成的模型不准确。

(2)Name。从语言本身或词源学角度而言，姓名包含极多信息，主要可以分为两类。其一为性别和年龄的混合信息，通过前缀Mr.(男)、Mrs. (已婚女)、Miss.(未婚女)，可以简单判定性别和粗略的年龄信息。当样例使用其他前缀(比如Rev.、Don.等)，可以通过姓名单词本身进行查询，男女姓名在英文语境中有明显差异，可通过单词本身判定其性别；女性在婚后会冠以夫姓，其family name(姓)为男名还是女名可以得出婚姻状况，从而简单推断出女性年龄。其二，通过Name中的前缀(prefix)，可以划分社会地位，prefix共有18类，具体信息如表2所示。

Name看似繁杂无从下手，实际根据prefix发现Name可以通过分类类别的信息增益方法来选取特征进行拟合，此步骤为初步预处理。为避免因为nominal变量过多导致使用算法产生分支过多，产生过拟合和过多剪枝步骤(unpruned)或者反复调节minNumObj(叶子节点个数)，将类似属性合并。经分类筛选，发现Name派生属性可按照两种分类方式，其一通过性别和年龄的混合信息如[Mr.(包含Master., Jonkheer.等其他前缀), Miss.(Mlle.), Mrs.( Ms., Mme.)], (0, 1, 2)；其二通过社会地位和性别的混合信息如[Sir.(Capt., Don., Major., Col. ,Sir.), Lady.( Dona., Lady., the Countess.)], (3,4,5)。

表2 Name属性详解

(3)Sex。在时代背景和西方一贯秉持的“女士优先”原则下，存活率定性来看显然与性别高度相关，女性存活率应当显著高于男性。

(4)Age。定性来看，由于先让妇女和小孩逃生的观念根植于西方传统，年龄较小的孩子相较于其他存活率应较高，年龄较大的老人可能因为行动不便、反应问题、运动能力、身体机能等原因难以存活。

(5)SibSp。同船(堂)兄妹及配偶个数，由于事发时正值深夜，当同船有(堂)兄妹或配偶时，可以及时通知，互帮互助，一起逃生。但当亲属个数过多时，可能由于船舱位置距离、通知时间等顾此失彼，导致一起丧生，因而SibSp数值跟生存率有较大相关性，且开始为正相关，超过一定量时为显著负相关。

(6)Parch。同船父母及孩子个数，由于孩子在逃生中优先，父母因为需要照顾孩子会得到更多的帮助和救援。而与SibSp属性类似，如个数过多，常常适得其反。但需要注意的是，由于是将父母和孩子的个数一起统计，当成年人带着父母时，由于需要照顾老年人，成年人可能存活率更低。因而，该属性从定性方面对预测变量Survived的影响和其影响程度难以断定。

(7)Ticket。船票编码，String型变量，有全数值，也有字母和数字的组合集合。进一步对数据分析发现约25%的数据有前缀，前缀共45种，其中由于“，”和“/”两种字符导致结果看似复杂。简要列举：SOTON/OQ，C.A.，非常明显，以字母开头的船票记录的是地点，SOTON为Southampton英格兰南安普顿(泰坦尼克号起航地)，C.A.为California美国加利福尼亚州，综合Embarked属性信息和泰坦尼克号航线(从英国南安普敦出发，途经法国瑟堡-奥克特维尔以及爱尔兰昆士敦，驶向美国纽约)，字母简称代表的地点应为船票出售地，定性来说，跟预测变量Survived相关性不大。数字部分经过查询现存文献和历史背景信息，经分析可知以1、2、3开头的大多为一、二、三等舱，4～9开头的大都为三等舱。

另外，值得注意的是，Ticket数字编码中的部分数据完全相同，应为套票(如家庭票)，通过统计分析可以了解家庭成员个数。由于析出属性和Parch、SibSp高度一致，目前设想应为冗余变量。但在做定量分析之前，先将Ticket按照首位数字进行分类(1，2，3～9)赋值为(1，2，3)。

(8)Fare。票价，票价越高，舱位会更好(一等舱)，拥有更好的时机及时收到讯息，同时拥有更多的资源如救生艇，因而应与预测变量Survived相关性高。但是需要注意的是，简单处理发现Fare属性标准差(StdDev)很大，接近56，均值和最大值值差也很大。结合对Ticket数据的分析，部分船票编码数字数据有重复，结合Parch、SibSp属性和和票价船舱等级，已知购买的票为套票(如家庭票)，因而需将团体票的票价进行数据处理，得到人均票价，使得数据科学、合理。

(9)Cabin。数据为字母和数字的组合，图1为舱位详解。

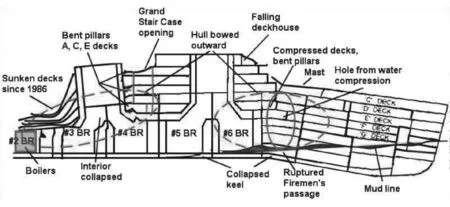
图1 Titanic 舱位图

从舱位可以分析出Pclass信息。除此之外，由于当灾难发生时，冰山造成右舷船艏至船中部破裂，五间水密舱进水。因而Cabin数据能展现的相对甲板的位置对预测变量Survived也非常重要。如靠近冰山撞击漏水处生还率更低，或旁边是配电室的房间，由于漏水导致漏电使得住在配电室周围的乘客身亡，难以幸存。但是，Cabin缺失值687个，缺失率高达77%，在应用某些不允许有缺失值的算法时应当注意处理。

(10)Embarked。上船口岸，分别为Cherbourg、Queenstown、Southampton (C,Q,S)，泰坦尼克的航线为从英国南安普敦S出发，途经法国瑟堡奥克特维尔C以及爱尔兰昆士敦Q，驶向美国纽约。图2为主要航线图。

由于泰坦尼克从S出发，途经C地、Q地，人们有选择下船的机会，或者本身就不需要到终点站纽约，因而有很大的概率不经历海难；在C地，人们只能选择在Q地下船，或是到纽约；在Q地上船的乘客必定经历海难，因而按照存活率从高到低排序应为：S>C>Q。

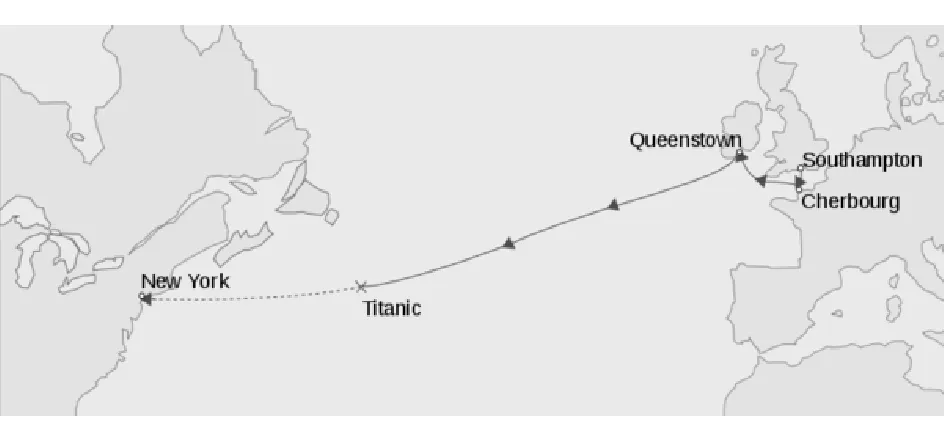
图2 Titanic 航线图

2.3 定量分析

总的概括一下数据特征，有缺失值、数据离散、部分属性经过特征工程处理可析出信息，直观的想法是利用决策树模型，尤其是Random Forest，可自动填补缺失值，避免由于手动填补造成数据噪声大。为了更好地运用多种算法比较优劣，进行皮尔孙相关热图(Pearson Correlation Heatma)分析，编程方式如下：将String数据类型转化为float，处理变量Sex (male, female) (0,1); Name按照性别和年龄的混合信息分类 [Mr.(包含Master., Jonkheer.等其他前缀), Miss.(Mlle.), Mrs.( Ms., Mme.)], (0, 1, 2); Embarked：(S,C,Q) (0, 1,2)。

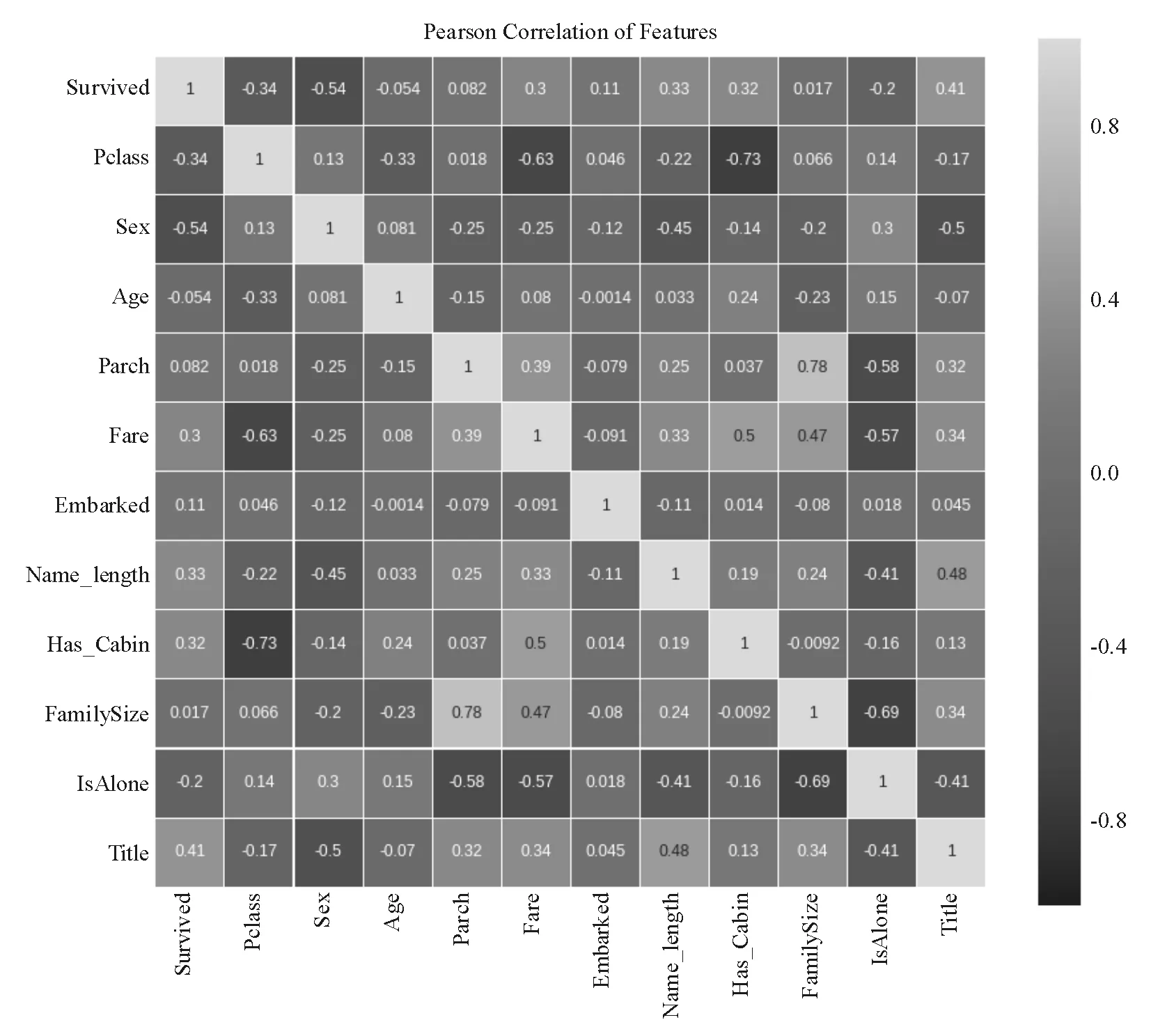
图3 皮尔孙相关热图

从图3皮尔孙相关热图中可看出没有太多的特征高度相关。因此，该数据集中没有太多冗余数据，每个属性都相对较为独立，用给出的属性特征训练模型使得模型更具有实践意义。同时，可以看到不同属性对预测变量Survived的相关系数，为进一步选择算法、处理数据，创造了条件。

使用Seaborn，生成配对图观察特征的数据分布，发现属性特征清晰，有利于模型拟合。

从该案例给出的数据出发，数据有缺失。其中：Embarked缺失量为2，缺失比例为0.22%；Age缺失量为177，缺失比例为19.87%；Cabin缺失量为687，缺失比例为77.10%；Embarked缺失量少，对模型拟合度影响不大；Age可以通过进一步分段求均值填补的方式手动填补；但是Cabin缺失量过多，人工填补可能造成数据噪声大。因此，优先考虑适合离散型变量的Random Forest，可自动填补缺失值。但是为了比较算法优劣，在应用其他需补齐缺失值的算法时，将Cabin缺失值默认为0。

3 研究结果

测试基线精确度(baseline accuracy)即ZeroR最大可能性分类，准确率(Correctly Classified Instances)为61.62%。从准确率百分比来看，挑选的四种算法显然表现不错(远高于基线精确度)。其中，综合决策树和Logistic的LMT表现相比其他算法好，准确率在6次拟合中相比其他三种算法都处于较高的位置；Random Forest由于较为适合案例数据，对缺失值处理较好，也有着不错的表现。简单来说，LMT六次拟合准确率均值最高为81.78，且标准差较小，为0.94。

考虑到过拟合问题，当训练模型准确率很高时，可能由于过拟合使得模型未抓住特征属性分析，导致测试集准确率低。根据Learning Curve判定模型所在状态，选取train_3尝试调节参数debug、minNumInstances，调节叶子节点样例个数，发现调节参数时准确率普遍在82.72%左右，在默认值为15时，LMT模型达到准确率最优值83.28%。

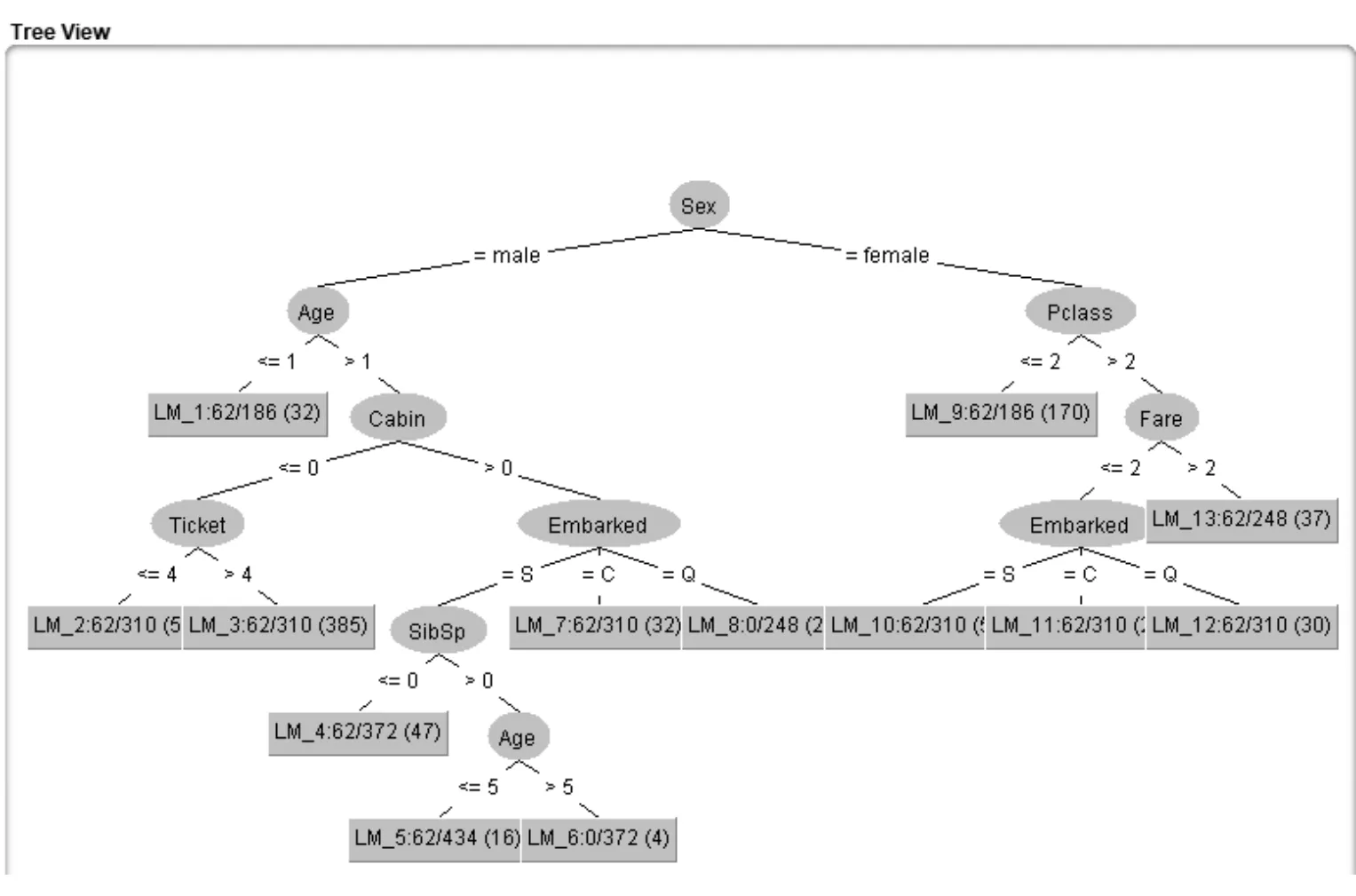
图4 LMT模型可视化展示

综合Kappa值为0.6354，MCC=0.641，ROC Area=0.864，PRC Area=0.858，该模型拟合度较好，Supplied Test Set得到准确率为85.65%。

通过Weka一级模型训练，选用dataset train_3.、LMT算法，如图4所示，模型拟合度最优。基于数据分析结果，分析得出：乘客在泰坦尼克海难中的幸存率与属性Name、Sex、Pclass、Age、SibSp、Parch、Fare、Cabin、Embarked高度相关。总的来说，身份为贵族，且船舱远离船体漏水位置，登船地点在Southampton的一等舱女性和小孩更容易成为幸存者，而这些因素实际上都是乘船者的客观因素。

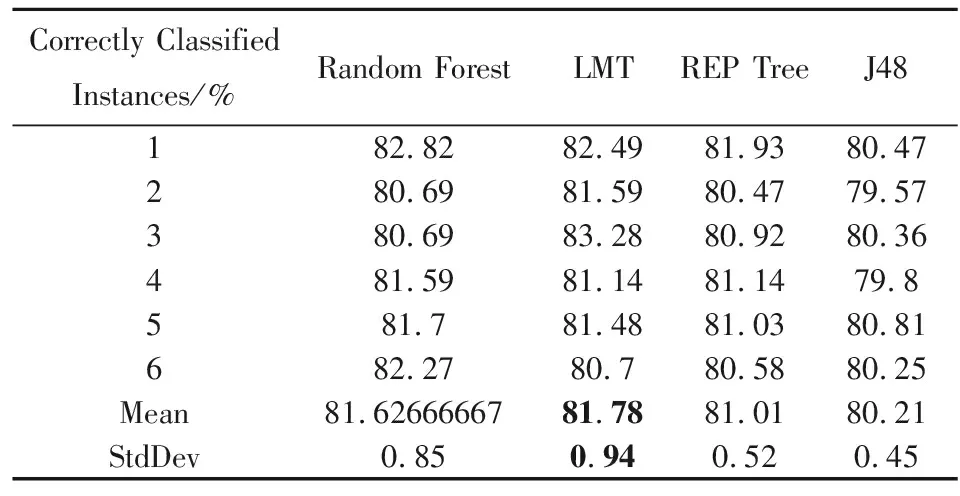
表3 算法的优度比较

4 结语

本文以泰坦尼克幸存者数据作为样本，构建了LMT模型，从定性和定量两个方面分析了乘客属性对幸存可能性的影响。研究发现乘客在泰坦尼克海难中的幸存率与属性Name、Sex、Pclass、Age、SibSp、Parch、Fare、Cabin、Embarked高度相关。模型拟合的准确率达到85.65%。换言之，基于LMT模型，如果该模型拟合度越低，船舶安全管理的可靠性应该越高，因为管理作为可变因素对幸存率造成了可观的影响。本研究对于海难等类似案例和目前船舶安全管理有一定参考意义。在未来的研究中，可以加入客观环境和管理情境，进一步探究影响海难事件中影响幸存率的因素。