考虑井阻变化的真空预压竖井地基固结解研究

张玉国, 万东阳, 韩 帅, 郑言林, 张丹贝, 黄 彤

(中原工学院 建筑工程学院， 河南 郑州 450007)

真空预压法是一种有效的软土地基加固方法，被广泛用于工程实践[1-10]。在真空预压竖井地基固结研究方面，有关学者已做出大量工作，取得了丰富的研究成果。董志良对堆载及真空预压砂井地基固结问题进行研究，给出了砂井地基固结解析解[1]；耿雪玉等采用Laplace变换半解析法，对基于真空-堆载联合预压法的未打穿竖井地基固结问题进行了分析研究[3]；张福海等考虑底部抽真空预压后，推导了砂井地基固结解析解[4]；李菲菲等考虑土体非达西渗流情况，对真空预压下竖井地基的固结问题进行了研究[5]；郭彪等较深入地研究了考虑真空联合堆载预压的竖井地基固结解析解[6-7]；周琦等求出了真空预压条件下砂井地基问题的Hansbo解[10]。

在传统的竖井地基固结理论中，多数研究基于理想井或不考虑井阻效应，这与工程实际情况存在一定的差异。在工程中，竖井引起的井阻效应对地基固结有不可忽略的影响。DENG等研究了排水量随深度和时间变化的竖井地基固结问题[11]；邓岳保针对堆载情况下竖井地基井阻随时间和深度变化的固结问题进行了研究[12]；LU等从井阻径竖向渗流耦合的非线性特点出发，求出了竖井地基固结解析解[13]；黄朝煊等考虑复杂荷载和井阻非线性情况，对地基固结问题进行了研究[14-15]；郭霄等推导了井阻随深度和时间变化的竖井地基固结精确解[16]。这些均是基于堆载预压的竖井地基理论研究，但基于真空预压荷载的研究还不多见。

本文针对井阻随时间变化的真空预压竖井地基固结问题进行研究，给出其一般解；将其与现有解析解进行比较，以验证本文解的正确性和合理性；基于该一般解进行算例分析，以探讨井阻变化对竖井地基固结特性的影响。

1 竖井地基固结数学模型

本文的数学模型，一方面是对竖井地基固结模型的简化(将其简化为二维计算简图)；另一方面是对受排水影响的土体性质的基本假定。

1.1 计算简图

图1所示为真空预压竖井地基计算简图。竖井地基顶面完全透水，底面不透水。其中，上部为砂垫层。

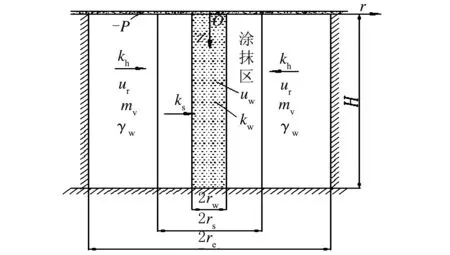
注：H为地基软土层厚度；r，z 分别为径向和竖向坐标；rw为竖井半径；rs为涂抹区半径；re为竖井影响区半径；kw为竖井的渗透系数；ks为涂抹区土体渗透系数；kh为原状土水平向渗透系数；mv为体积压缩系数；uw为竖井内任意一点的超静孔压；ur为土体内任意一点的超静孔压；γw为水的重度；-P为真空负压。图1 真空预压竖井地基计算简图

1.2 基本假定

基本假定如下:①土体完全饱和；②土颗粒和水都不可压缩，土体的变形完全由孔隙水的排出引起；③由于使用塑料排水板，只考虑径向渗流，且土体中水的渗流服从Darcy定律；④Barron等应变条件成立；⑤在任一深度从土体流入竖井的水量等于竖井中向上水流的增量；⑥井阻因竖井渗透系数在固结过程中逐渐减小而随深度和时间增大[9]，即竖井渗透系数kw随固结时间呈指数衰减，可表示为：

kw=kw0e-At

(1)

式中：kw0是竖井的初始渗透系数；A为试验常数；t为固结时间。

此外，假设真空度在竖井中不随深度改变。

2 变井阻的等应变径向固结基本方程及其边界条件

由于仅考虑径向渗流，因此根据文献[17]可得如下径向渗流固结基本方程：

(2)

基于等应变条件，有：

(3)

式中，εv为固结影响区任意一点的体积应变(与垂直应变相等)。

根据式(1)和基本假定⑤，有：

(4)

固结影响区任一深度的平均超静孔压为：

(5)

边界条件为：

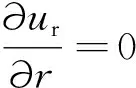
(6)

r=rw时，ur=uw

(7)

z=0时，uw=-P

(8)

(9)

利用边界条件(6)，在式(2)两边对r进行积分可得：

(10)

在式(10)两边对r再次进行积分，并根据边界条件(7)可得：

(11)

式中，s=rs/rw。

由式(10)以及r=rw得：

(12)

式中，n=re/rw。

把式(12)代入式(4)可得：

(13)

将式(11)代入式(5)，得到的平均超静孔压为：

(14)

式中，

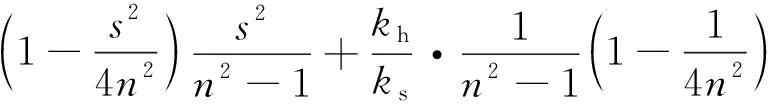
由式(3)、式(13)和式(14)可得：

(15)

(16)

由式(15)、式(16)可得uw的控制方程，即：

(17)

3 变井阻等应变的径向固结基本方程求解

根据分离变量法，令uw(z,t)=Z(z)T(t),并将uw(z,t)代入式(17)，可得：

(18)

由式(18)和边界条件(8)和(9)可得微分方程的特解，即：

uw=-P+Amsin(βz)·

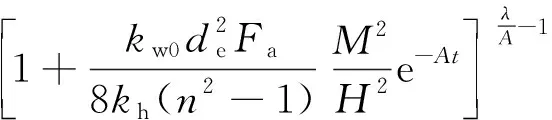
(19)

叠加所有特解，得到的真空预压下竖井内孔压为：

(20)

对式(20)化简，可得：

(21)

(22)

由式(21)、式(22)和式(3)可得：

(23)

将式(21)和式(23)代入式(11)，可得土体内的超静孔压解，即：

(24)

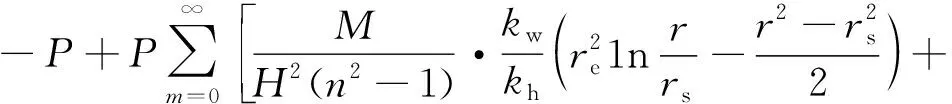
(25)

由式(21)、式(22)和式(16)，可得竖井地基(土体)任一深度的平均超静孔压解，即：

(26)

竖井内孔压解为：

(27)

因此，土体任一深度的径向固结度为：

(28)

土体任一深度的径向总平均固结度为：

(29)

进一步分析发现，当A趋近于0时，有：

(30)

根据式(30)，可将土体任一深度的径向总平均固结度退化为：

(31)

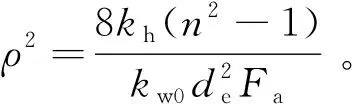
由式(31)可知，本文解可以退化为董志良真空预压下的解。

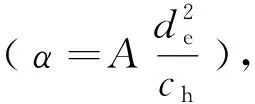
(32)

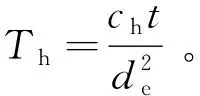
将式(32)代入式(26)、式(28)和式(29)，可得：

(33)

(34)

(35)

4 算例分析

利用式(30)可验证本文所得解的正确性和合理性，而且通过选取不同参数进行数值计算，可分析井阻变化对竖井地基固结特性的影响。

计算竖井地基固结解析解时选取的参数如下：rw=0.035 m，rs=0.175 m，n=re/rw=10、15、20，s=rs/rw=5，mv=0.2 MPa-1，H=20 m，kh=2.0×10-8m/s，kh/ks=5、4、2、1，kw0=1.0×10-3m/s。

(1) 在n=15，α取不同值的情况下，变井阻的竖井地基固结特性如图2所示。由图2可知，当α从0.01缓慢增大时，竖井地基的固结速率慢慢减小，这就说明以往采用无井阻的固结解析解会高估竖井固结速率；当时间因子Th很小时，变井阻效应对固结计算结果影响很小，当Th>0.5时，变井阻效应对固结计算结果会产生较大影响；当α=0.5、0.8和1.0时，固结后期的固结度分别停留在87%、74%和67%，这说明当井阻足够大时，竖井地基的径向固结过程会停止。

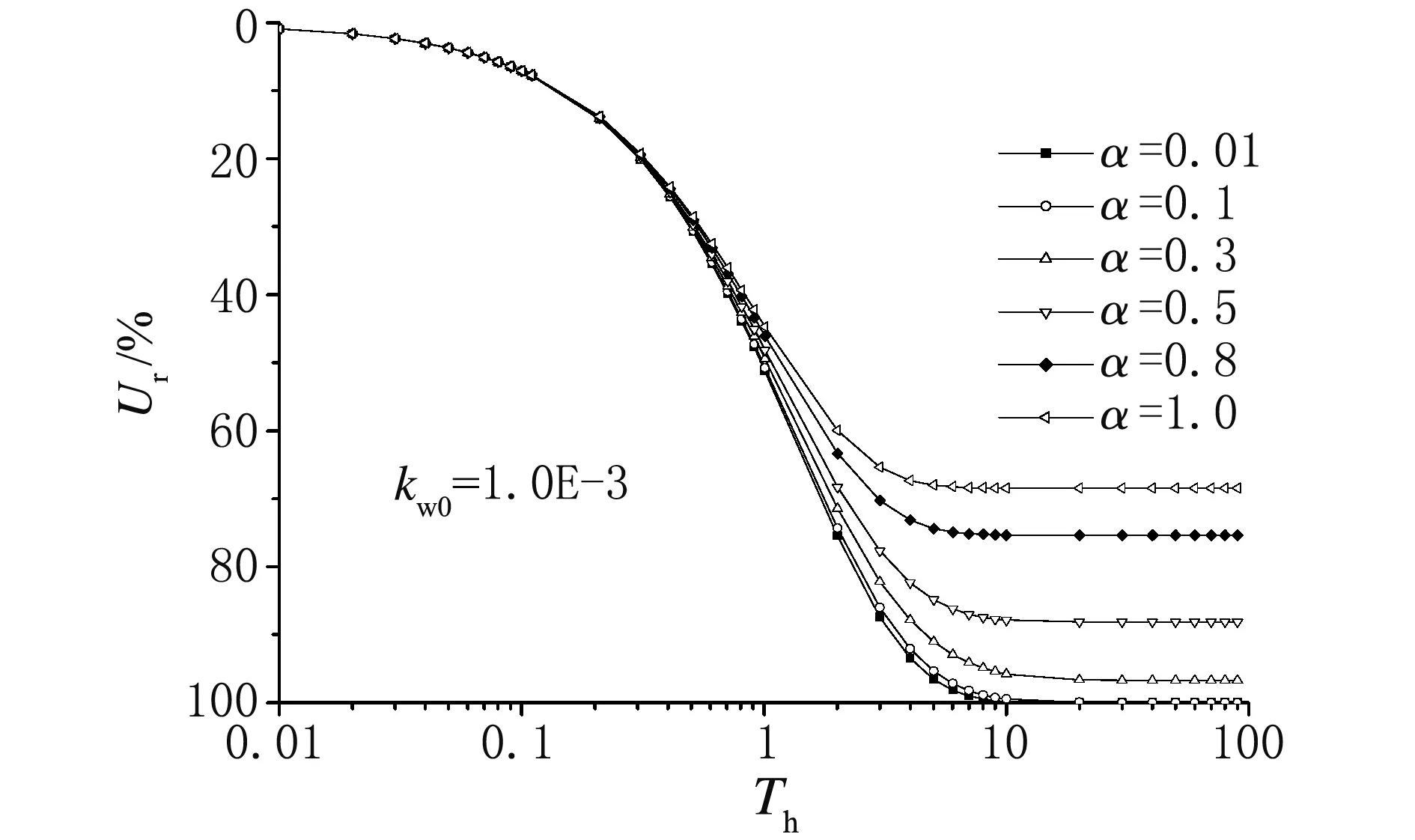
图2 n=15时变井阻的竖井地基固结特性

(2) 图3所示为n和α对竖井地基固结特性的影响。分析图3可知，α为定值时，n越大，固结速率越小；n为定值时，α越大，固结速率越小；n值的变化对竖井地基固结特性的影响并不显著。

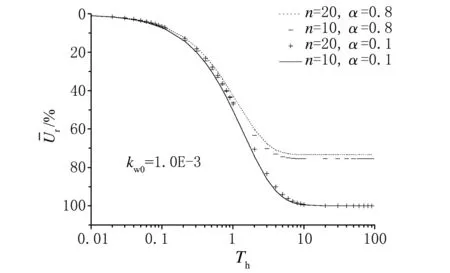
图3 n和α对竖井地基固结特性的影响

(3) 图4所示为初始渗透系数对竖井地基固结特性的影响。对比图4中(a)和(b)可知：竖井初始渗透系数越大，井阻对竖井地基固结特性的影响越不明显；当α>0.3时，初始渗透系数大的比初始渗透系数小的竖井地基固结速率大。

(a) kw0=1.0E-3

(b) kw0=3.0E-3图4 初始渗透系数对竖井地基固结特性的影响

(4) 不同时间节点的α取值对竖井地基任一深度固结度的影响如图5所示。当时间因子很小的时候，竖井地基固结度随地基深度的变化受α值的影响不明显；但随着时间因子的增大，固结度随地基深度的变化受α值的影响越来越明显。

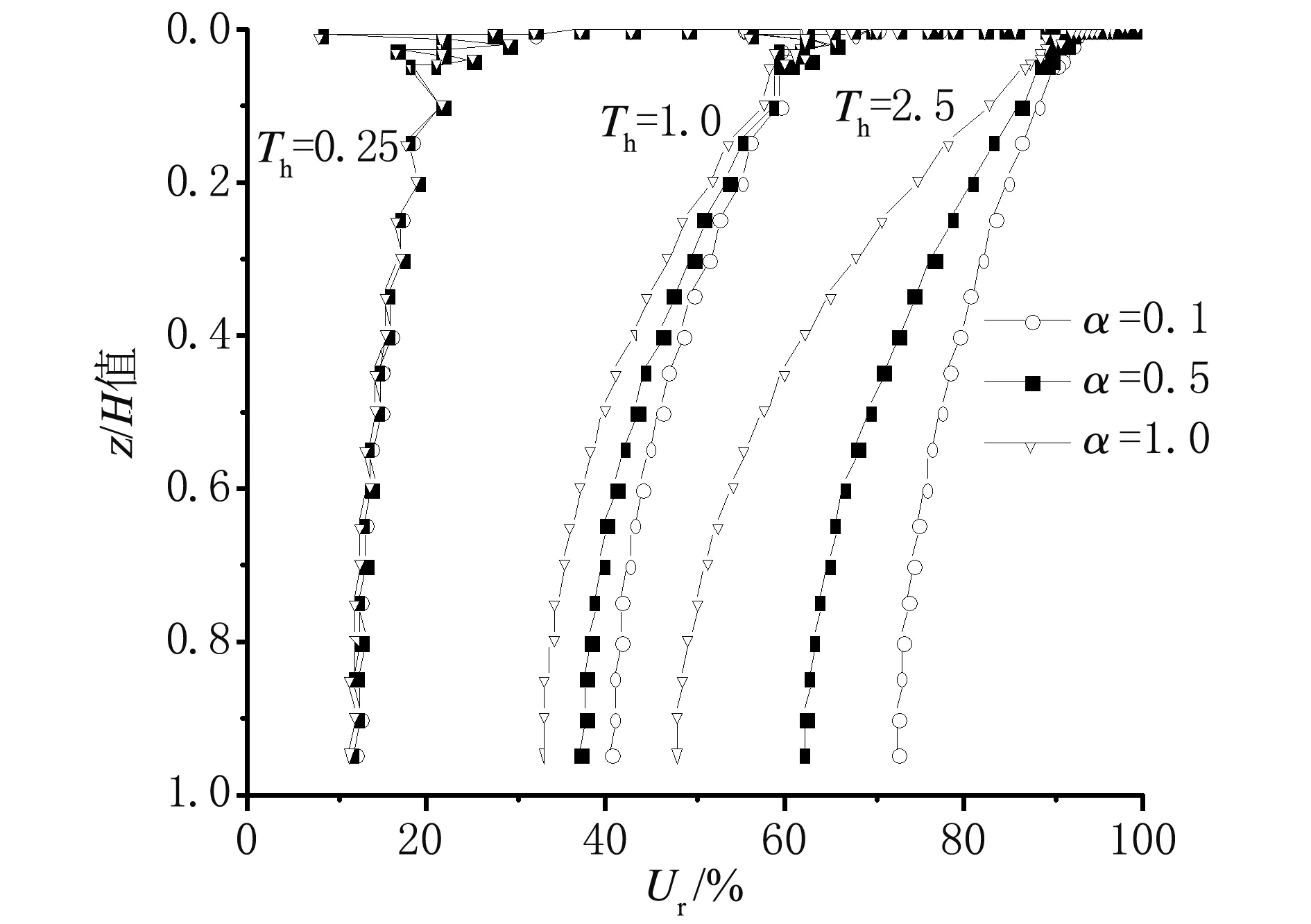
图5 不同时间节点的α值对竖井地基任一深度固结度的影响

(5) 图6所示为真空负压为-80 kPa时竖井地基任一深度平均超静孔压的分布情况。由图6可以看出，α取值越大，平均超静孔压随地基深度增大而消散得越慢。

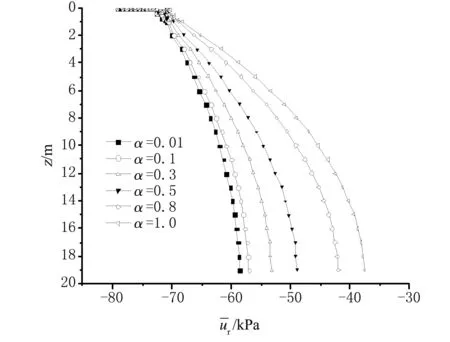
图6 真空负压为-80 kPa时竖井地基任一深度的平均超静孔压分布情况

(6) 图7所示为径向渗透系数对竖井地基径向总平均固结度的影响。从图7可以看出，kh/ks越小，地基固结速率越大。这说明，竖井对土体的扰动越小，越有利于地基固结。

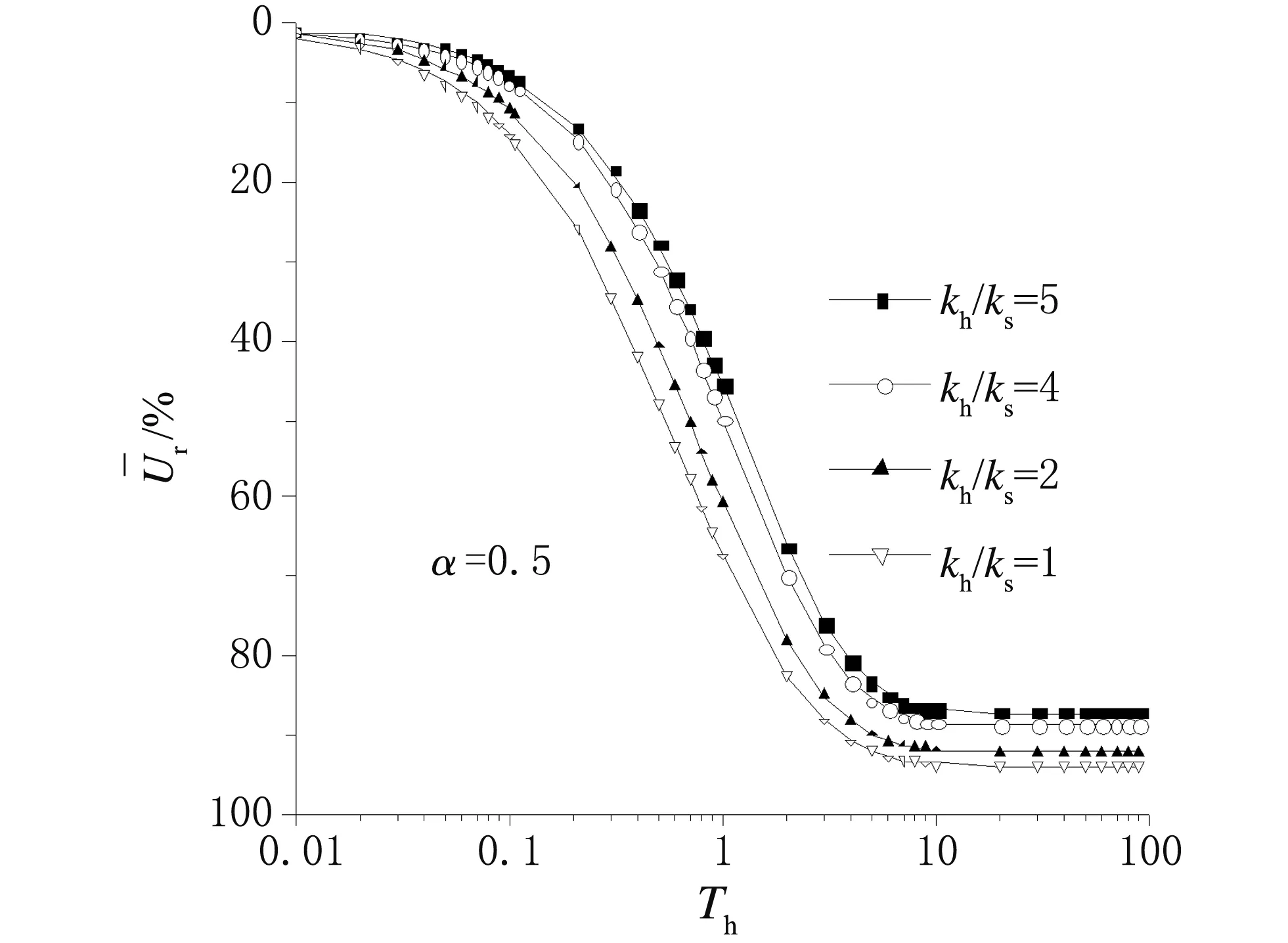
图7 径向渗透系数对竖井地基径向总平均固结度的影响

(7) 图8所示为不同真空度下竖井地基任一深度的平均超静孔压分布情况。从图8可以看出，不同真空度预压下，平均超静孔压随地基深度增大而消散的速率差异明显，真空度越大，消散速率越小。

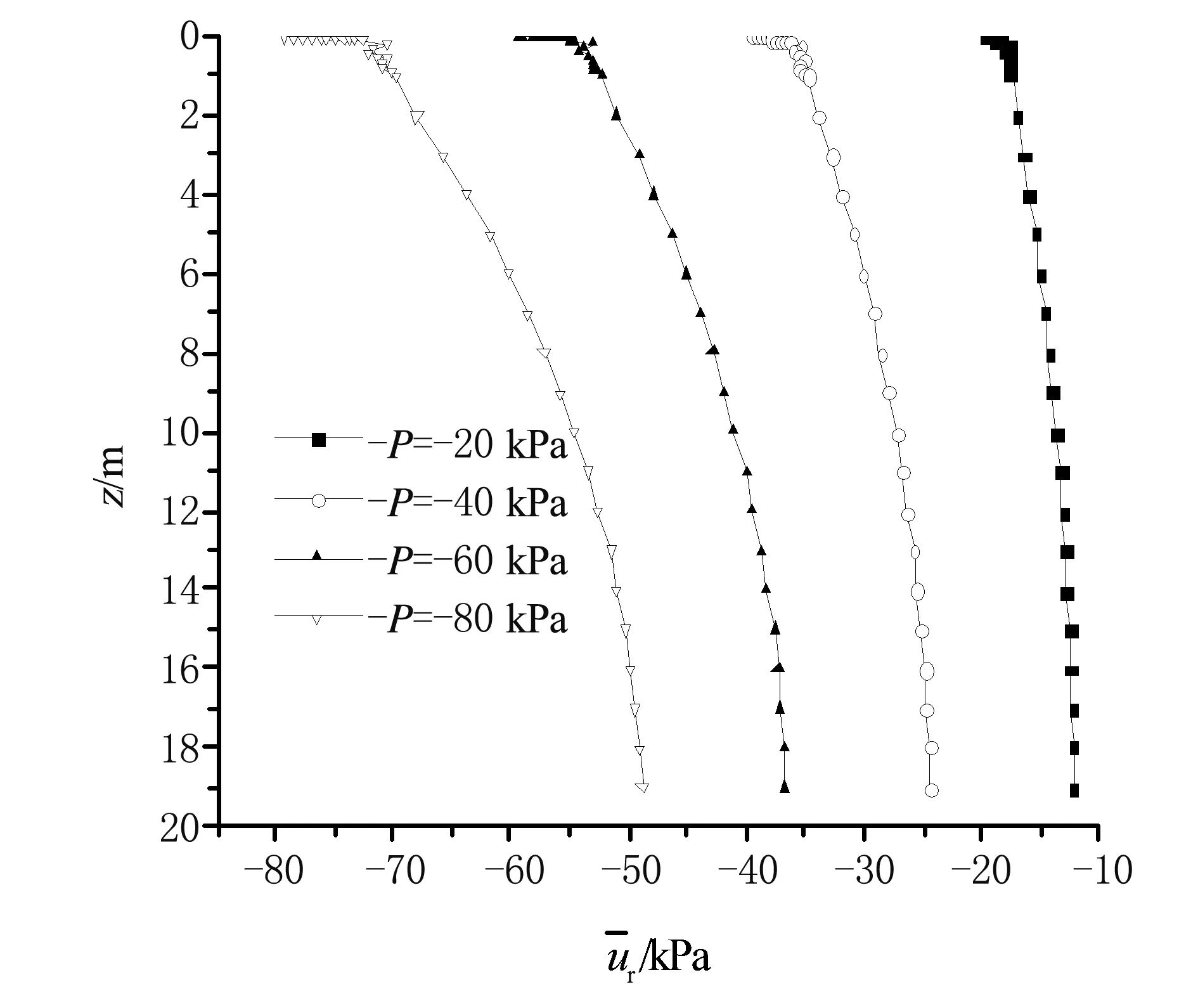
图8 不同真空度下竖井地基任一深度的平均超静孔压分布情况

5 结论

(1) 对竖井渗透系数随时间变化的固结问题进行求解，推导出真空预压下井阻随时间变化的固结解析解，并将该解与现有真空预压竖井地基固结解析解对比，验证了该解的正确性与合理性。

(2) 受井阻影响，竖井地基的固结速率随时间延长而降低，且井阻越大，对固结速率的影响越大，当井阻增大到一定值时，竖井地基的径向固结趋于停止。此外，竖井的初始渗透系数越大，井阻对固结的影响就越小；竖井对土体的扰动越小，竖井地基的固结速率就越大。

(3) 在不同真空荷载下，土体任一深度的平均超静孔压随深度增大而迅速消散，真空度越大，消散得越慢。