基于模态分析优化大型复杂焊接构件振动时效参数的研究
张晓睿, 董学武, 李 兵, 王东强, 陈文广, 张君浩, 李 彪, 宋志强
(1.郑州恒天重型装备有限公司 质量部, 河南 郑州 450007; 2.中原工学院 机电学院, 河南 郑州 450007; 3.郑州市污水净化有限公司 技术部, 河南 郑州 450052)
振动时效是一种消除金属构件残余应力的新技术,具有节能环保、效率高、成本低但技术复杂的特点,其消除残余应力的效果受制于振动参数的适切性[1]。大型复杂焊接构件的尺寸庞大、结构复杂、刚度较高、焊接残余应力分布复杂且相互牵制,消除其残余应力的技术难度较大[2]。因此,研究振动消除复杂焊接构件残余应力的激振参数优化问题具有重要的学术价值和实际意义。
压力室为结构复杂的大型焊接构件,在工作过程中需要承受巨大的压力和高温,极易发生损坏。其一旦损坏,导致的后果将是无法估量的。因此,保证压力室的承载能力和结构稳定性尤为重要。压力室焊接残余应力的存在,会导致应力集中、应力腐蚀、变形等问题,严重影响其力学性能、承载能力和结构稳定性[3]。因此,必须对压力室进行消除焊接残余应力处理。本文采用模态分析方法,对压力室进行振型测试,并依据压力室固有频率、振型和焊接残余应力分布,对压力室振动时效技术参数进行优化。
1 压力室的模态分析
1.1 模态分析原理
将压力室视为n自由度振动系统,则其运动方程为:

(1)
式中:[M]、[C]、[K]分别为系统的质量、阻尼和刚度矩阵;{x}及{f(t)}分别为位移响应向量和激励力向量,可具体表示为:
对式(1)两端分别作初始条件为零、变量为s的拉普拉斯变换,可得:
(s2[M]+s[C]+[K]){X(s)}={F(s)}
(2)
式中,{X(s)}和{F(s)}分别是X(t)和f(t)的拉氏变换。
令
[Z(s)]=s2[M]+s[C]+[K]
(3)
即

(4)
式(4)中矩阵为n阶方阵,也可称为阻抗矩阵。因为[M]、[C]、[K]都是对称方阵,所以该阻抗矩阵也是n阶对称方阵。
可将式(2)写为:
[Z(s)]{X(s)}={F(s)}
(5)
传递函数矩阵为:
(6)
式中:N(s)=adj[Z(s)],为Z(s)的伴随矩阵;D(s)=det[Z(s)],为[Z(s)]的行列式。
由式(6)可知,[H(s)]中任一元素Hlp(s)可表示为:
(7)
即
(8)
则
(9)

(10)
由式(10)可得压力室的固有频率ωi和模态阻尼ζi。
留数矩阵为:
(11)
由式(11)可得压力室的模态振型{φ}i。
1.2 压力室振型测试
对压力室进行几何建模后,采用美国DP公司动态信号分析系统和法国N-Modal模态分析系统[4],对压力室进行导纳测量和参数识别,可得压力室的前5阶固有频率和振型。压力室振型测试系统如图1所示。

图1 压力室振型测试系统
1.3 压力室振型测试结果
表1所示为压力室的前5 阶固有频率。对应的压力室前5阶振型如图2所示。

表1 压力室前5阶固有频率 Hz
2 压力室的振动时效
2.1 振动时效参数优化
根据表1所列压力室的前5 阶固有频率,结合振动时效机的振动频率范围,可优化压力室振动时效激振频率、支撑点、激振点等关键技术参数。由于消除压力室残余应力的技术难度很大,故采用两次振动时效。为了消除压力室各点尤其是应力集中点的残余应力,两次振动过程中压力室各点都应充分振动。本文以压力室残余应力分布及不同的低阶固有频率和振型,作为压力室振动时效激振频率、支撑点、激振点等关键技

(a) 第一阶振型

(b) 第二阶振型
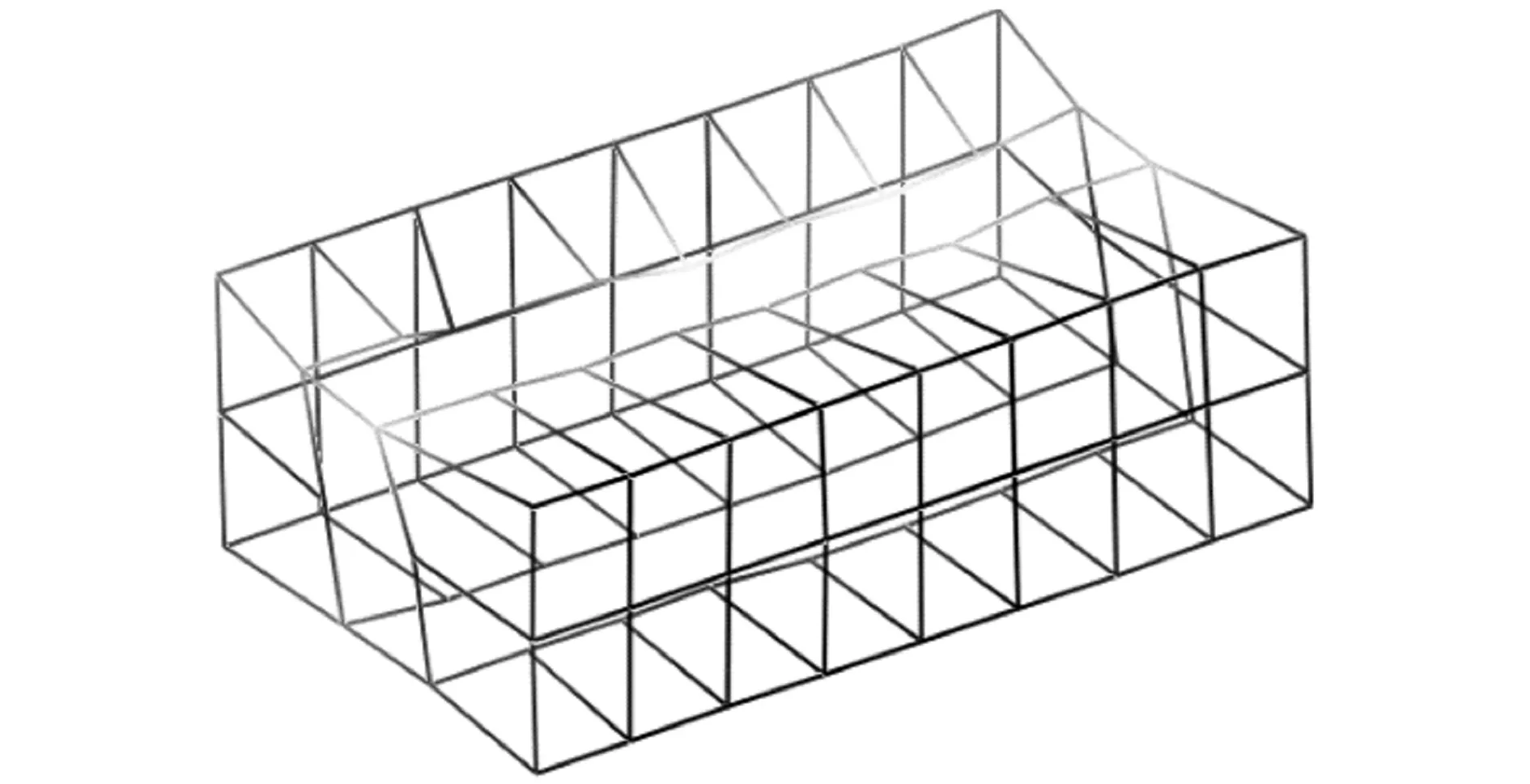
(c) 第三阶振型
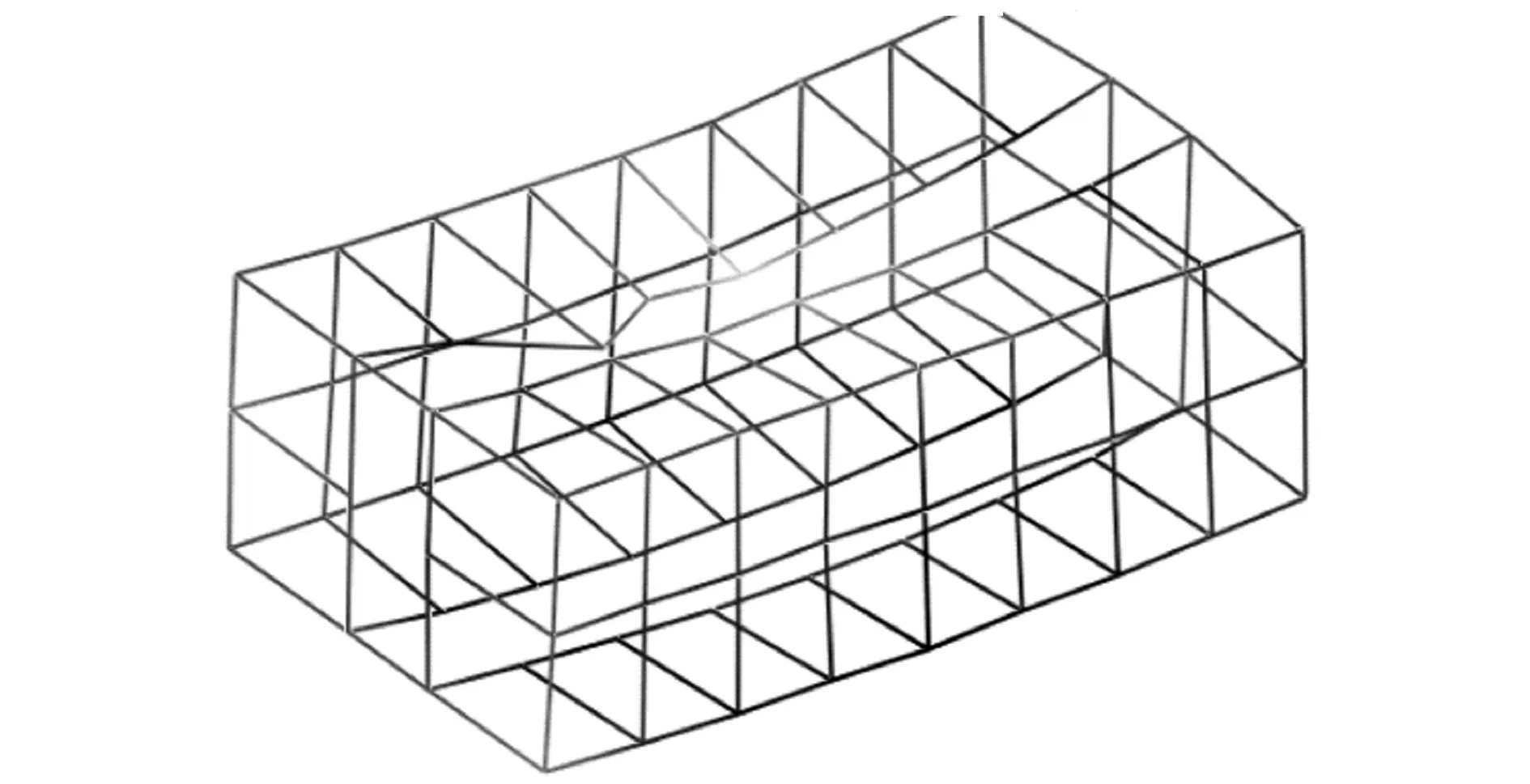
(d) 第四阶振型

(e) 第五阶振型图2 压力室前5阶振型
术参数的设计依据。
(1) 激振频率。根据经验,当激振频率等于低价固有频率时,用较小的激振力即可使压力室以较大的幅值振动而且振动的分布均匀,这不仅可降低能量消耗,而且能用最小的激振力来激发足量的振动幅值[5-7]。因此,激振频率是保证振动时效处理效果的关键技术参数。根据压力室的低阶固有频率和振动时效机激振器的转速范围,第一次振动时选择压力室第一阶固有频率作为激振频率,对应的激振器转速为1 150 r/min;第二次振动时选择压力室第二阶固有频率作为激振频率,对应的激振器转速为5 122 r/min。
(2) 支撑点。为了保证对压力室的振动激发,支撑点应选在与激振频率对应的压力室模态振型的节点处[6]。考虑到压力室为结构复杂的大型焊接构件,第一次振动时选取压力室第一阶振型的4个节点作为支撑点位置;第二次振动时选取压力室第二阶振型的4个节点作为支撑点位置。
(3) 激振点。激振点选在与激振频率对应的压力室模态振型的波峰处,以便用最小的激振力来激发较大的振动幅值。同时,应根据压力室的残余应力分布情况选取激振点,使压力室的应力集中部位得到充分振动[7-9]。按照以上要求,两次振动的激振点可分别选在压力室第一阶振型和第二阶振型的波峰处。
(4) 激振力。采用以压力室低阶固有频率及对应振型确定的激振频率、支撑点、激振点等关键技术参数进行振动时效处理时,较小的激振力即可激发幅值较大的振动。机械式振动时效机激振器的激振力为偏心质量机构旋转产生的离心力。通过调节其偏心档位,可改变激振力的大小。因此,激振器的偏心档位设置应保证压力室产生适当的振幅,但激振力最高不能超过额定载荷的70%[7]。本文通过试振发现,当第一次振动和第二次振动的激振器偏心档位分别选为30°和70°时,压力室振动能够满足振幅要求。
(5) 激振时间。在振动时效中,位错发生移动、增殖、再移动、再增殖,到最后稳定,需要一定的时间。若构件在较大的动应力作用下激振时间过长,则构件的疲劳寿命会受到影响;而激振时间过短又达不到振动时效的处理效果。焊接构件的材料、重量、结构、残余应力不同,所需振动时效的激振时间也不同,按经验一般取15~30 min。考虑到压力室的结构特点及其焊接残余应力的分布情况,本文采用的两次振动时间均为20 min。
振动时效技术参数如表2所示。

表2 振动时效技术参数
注:激振器的激振力通过其偏心档位调节,激振效率通过其转速调节。
2.2 振动时效工艺实施
(1) 支撑压力室。按照表2所示第一次振动支撑点位置,将压力室可靠地支撑在振动时效专用的4个橡胶垫上。
(2) 安装激振器及拾振器(又称加速度传感器)。按照表2所示第一次振动激振点位置,将激振器可靠地安装到压力室上。将拾振器安装在距激振点一定距离的压力室第一阶振型的其他波峰附近。
(3) 激振。首先仔细检查,确认已完好地支撑压力室并可靠安装激振器和拾振器,依据表2所示第一次振动激振参数,对压力室进行第一次振动时效;然后,依据表2所示第二次振动激振参数,调整压力室支撑点、激振器和拾振器安装位置,并仔细检查,在确认可靠后对压力室进行第二次振动时效。
2.3 振动时效效果评定
按被测件的损伤程度,现有的残余应力测量方法可分为有损和无损两大类。压力室的特殊用途决定了在测量其残余应力时不能被破坏,因此可采用无损测量的X射线法应力测量技术,对压力室进行处理。本文采用X射线衍射应力测量法分别测定压力室振动时效前后各测点表面的宏观残余应力,在压力室焊接区域选取了均匀分布的22个残余应力测点。
选用X-350A型X射线衍射仪,采用侧倾固定 法,以金属晶体衍射峰偏移作为应力测定的依据 ,通过精测衍射峰位的方法确定对应的应力值[10-11]。残余应力测试条件如表3所示。

表3 残余应力测试条件
3 振动时效结果分析
压力室振动时效前后所测焊接残余应力如图3所示。压力室焊接残余应力的振动时效前后对比如表4所示。
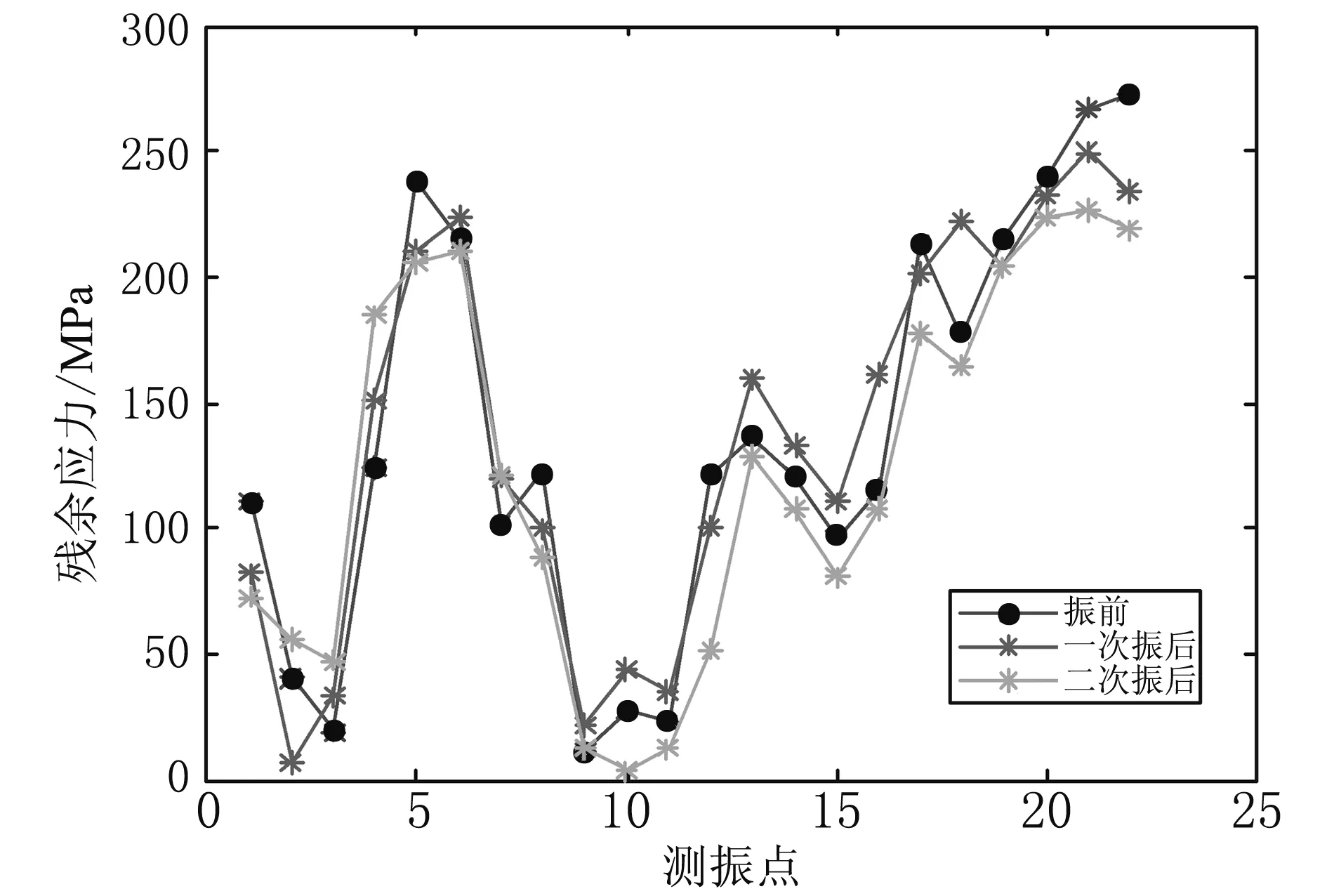
(a) 横向残余应力
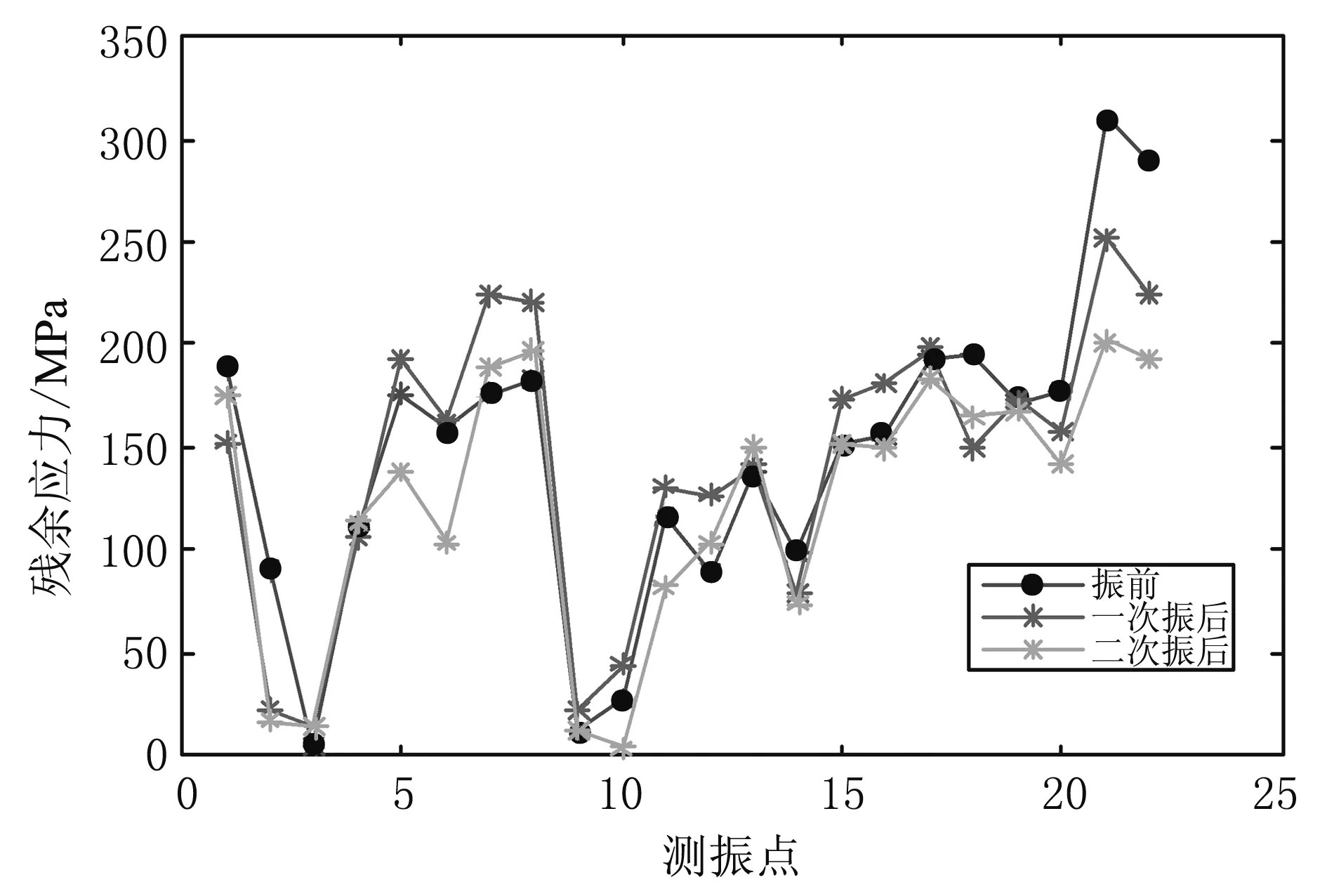
(b) 纵向残余应力
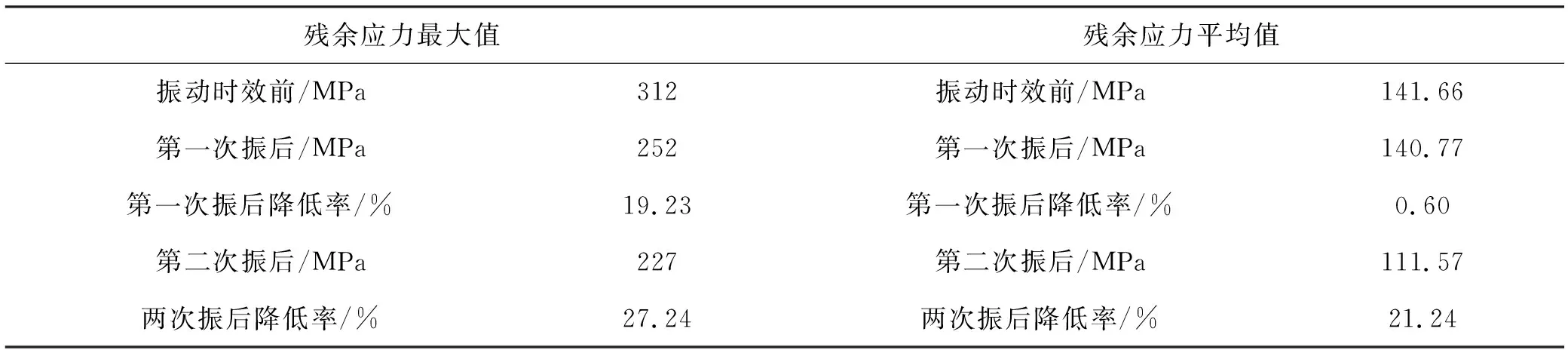
图3 压力室振动时效前后焊接残余应力
从表4可以看出,振动时效前残余应力最大值为312 MPa,残余应力平均值为141.66 MPa;第一次振动后残余应力最大值的降低率为19.23%,残余应力平均值的降低率为0.60%;两次振动后残余应力最大值的降低率为27.24%,残余应力平均值的降低率为21.24%。这说明,基于模态分析优化激振参数的振动时效技术,对尺寸庞大、结构复杂、刚度较高焊接构件进行振动时效处理,效果是良好的。
4 结语
本文采用模态分析方法测试压力室固有频率和振型后,依据压力室的残余应力分布及其固有频率和振型对压力室振动时效技术参数进行了优化。经过两次振动时效处理,压力室残余应力最大值和平均值均明显减小,压力室的承载能力和结构稳定性得到了提高。基于模态分析优化激振参数的振动时效技术,对降低尺寸庞大、结构复杂、刚度较高焊接构件的残余应力具有良好效果。

