多轴同步收放卷系统建模与自适应控制
石贤可, 温盛军
(1.中原工学院 电子信息学院, 河南 郑州450007; 2.中原工学院 中原彼得堡航空学院, 河南 郑州 450007)
多轴同步收放卷系统是工业现场中经常使用的电气控制系统,收放卷系统在钢铁厂、造纸厂、印刷厂、纺织漂染厂、食品厂、燃料电池厂应用广泛,涉及轧制、拉拔、压花、涂层、印染、清洗以及卷绕等工序,其作用是控制卷材的张力,使其保持稳定[1]。曾有学者利用动力学建模方法得出了多轴同步收放卷系统开卷机构的数学模型,并认为,多轴同步收放卷系统张力控制的关键是解决速度对张力影响较大的问题[2-3]。陈耀等针对PID (Proportion Integration Differentiation)算法不能解决控制模型突变时动态响应不佳问题,设计了模糊PID控制器[4]。马文明等研究了内模控制算法在多轴同步张力控制系统中的应用[5]。智能控制算法在多轴同步张力控制系统中的应用,从不同程度上解决了张力控制系统存在的问题。
本文通过推导多轴同步收放卷系统的数学模型,设计基于模型参考自适应算法的张力控制器,试图解决以PID算法为张力控制器时系统启动、升减速阶段存在的张力波动过大问题;并且将该控制器应用于收放卷系统,采集相关数据,观察收放卷系统升减速阶段的张力变化,以确定该控制器的应用效果。
1 多轴同步收放卷系统结构及数学模型
1.1 多轴同步收放卷系统的结构
图1所示为典型的多轴同步收放卷系统结构。在收放卷系统运行中,放卷装置的卷径不断减小,收卷装置的卷径不断增大。通过收卷与放卷,物料按图1所示从右至左通过工艺区。对物料按相关工艺处理时,常常要求张力是恒定的,如薄膜行业的有些加工工艺就要求收卷和放卷环节张力恒定。放卷环节,物料拉着放卷电机转动,且放卷电机输出相应的制动转矩而充当阻力,使物料的张力发生变化;收卷环节,收卷电机输出转矩充当卷绕动力,也会使物料的张力发生变化。
在图2所示的西门子多轴同步收放卷系统样机中,左中为收卷轴,右上为放卷轴,中间有两个随动辊和一个夹紧装置,左上为张力传感器(用于测量卷材的张力),编码器则紧邻张力传感器(用于测量卷材的线速度)。该系统以西门子CPU-315T为控制器,S120为变频器,用于控制左右两台伺服电机,协同完成收卷和放卷过程,并使张力恒定。
1.2 多轴同步收放卷系统的数学模型
1.2.1 收卷环节的动力学分析
这里以收卷环节为研究对象。收卷电机工作在转矩模式下(见图3)。图3中:Md为电机轴(或称减速器)输出转矩;D为收卷卷径;D0为卷辊直径;ω为开卷辊的角速度;v为卷材线速度;b为卷材宽度。收卷环节的动态力矩方程为:

图1 典型的多轴同步收放卷系统结构

图2 西门子多轴同步收放卷系统样机
(1)

图3 收卷电机的转矩工作模式
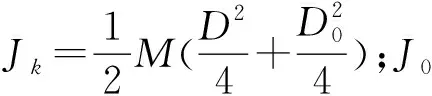
假定在系统加速瞬间,卷材转动惯量Jk不变且收卷卷径D不变,则可推导出:
(2)
这里,v=D·ω/2。
由式(2)可知,卷材张力T主要受卷材线速度v(可测量)、收卷卷径D(可测量)的影响,且张力是关于卷材线速度及其导数、收卷卷径平方及其四次方的多项式。由此可见,收放卷系统是一个多输入多输出系统,具有参数不确定性,并极易受卷材线速度的影响[6]。式(2)中不可直接测量的参数为电机卷辊轴的转动惯量J0和摩擦系数Bf,其他参数均可直接测量或由计算得出。通过辨识方法辨识图4所示电机及减速器相关参数可知,J0=5×10-5kg·m2,对应于图4中P1498[0]。
在收放卷系统中减速器的减速比为50∶1,假若减速器无功率消耗,输入功率与输出功率相当,则减速器输入速度与输出速度比为50∶1,减速器输入转矩与输出转矩之比为1∶50。这里以电子胶片为实验卷材,可测量或计算出如下相关参数:D0=0.076 m,b=0.035 m,Bf=1.9,ρ=1 380 kg/m3。

图4 电机及减速器相关参数
1.2.2 伺服电机输出转矩分析
本文采用西门子S120变频器驱动西门子伺服电机。S120变频器与电机之间采用DRIVE-CLIQ型智能通信电缆。伺服电机的输出转矩用双闭环PID来控制。变频器驱动的电机输出转矩模型为一阶系统,其转矩阶跃响应曲线如图5所示。
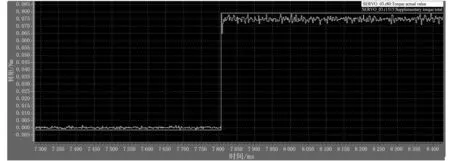
图5 变频器驱动的电机输出转矩阶跃响应曲线
图5中,参数r1515为总的转矩设定值,r80为电机当前的转矩值。对于给定的系统转矩值,电机可快速输出相应的转矩。以转矩设定Mdr为输入变量,实际电机输出转矩Mdk为输出变量,考虑到该收放卷系统装有减速比为50∶1的减速器,假定无功率损耗,功率相同情况下转矩与速度成反比,则系统实际输出的转矩与电机输出的转矩之比为50∶1。根据一阶系统的阶跃响应特征,可将S120变频器控制西门子伺服电机的输出转矩模型近似为:
(3)
式(2)中只有第一项中的Md是张力系统的可控输入,而它又是减速器的输出转矩。故可将式(2)第一项与变频器控制伺服电机输出转矩模型式(3)结合起来,推导出如下收放卷系统张力模型:
(4)
式(2)中后两项与转矩Md无关, 可看作系统的扰动,即
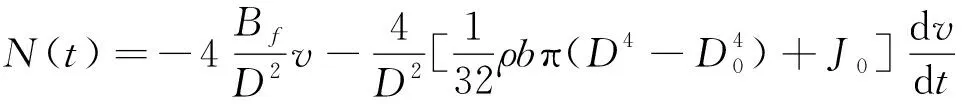
(5)
1.3 卷材线速度与张力耦合性分析
从式(2)可以看出,卷材张力受卷材线速度影响较大。但是,卷材的张力反过来是否对卷材线速度产生影响呢?这并不确定。
放卷电机工作在速度模式下,其转速与卷材线速度之间具有确定的数学关系。根据电机工作原理,可将卷材张力波动对放卷电机转速造成的干扰看作放卷电机负载的扰动。矢量控制电机的调速系统为双闭环(速度环和转矩环)调速系统,抗干扰能力较强[7]。由此可推断,卷材张力的波动并不影响放卷电机的转速,从而不会影响卷材的线速度。在电机运行时间为13 500 ms时,对电机施加较大的负载扰动,矢量控制电机的调速系统中转矩环及时输出相应转矩来平衡该扰动,电机转矩曲线会发生波动,但在速度模式下工作的电机转速并未发生波动(见图6)。这表明,卷材的张力变化对电机转速的影响极小,对卷材线速度的影响也极小。
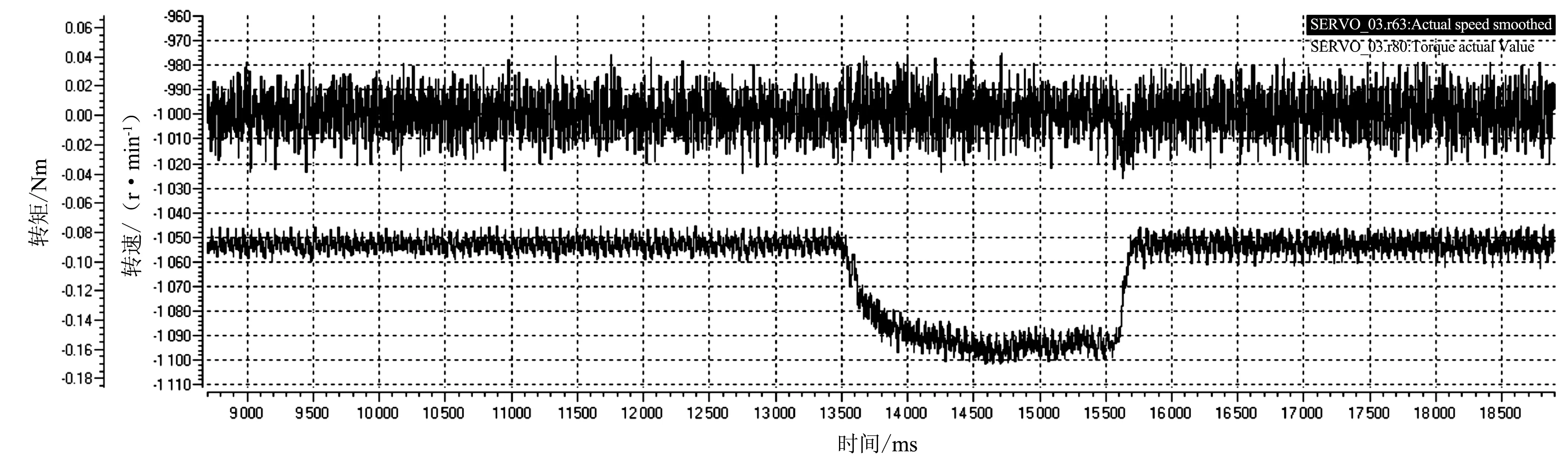
注:上方曲线为电机的转速曲线,下方曲线为电机的输出转矩曲线。图6 受负载干扰时电机转速与转矩曲线
2 基于模型参考自适应算法的多轴同步张力控制器设计
自适应控制器具有鲁棒性较好的特点。本文以文献[8]中基于李雅普诺夫稳定理论设计的模型参考自适应方法为基础,提出了图7所示状态空间方程描述的模型参考自适应系统。其中Kp、KU为系统的控制器。控制器的任务是找到Kp、KU的自适应律,使系统输出跟随参考模型的输出。

图7 状态空间方程描述的模型参考自适应系统
因李雅普诺夫稳定性是在时域中判定的,故可将控制模型等价转换为状态空间方程。转换后状态矩阵为:
(6)
参考模型应选取动态和静态响应特性较好的。时间常数较小的一阶系统的阶跃响应具有良好的动态和静态特性。本文选取的控制系统参考模型为:
(7)
式(6)转换后所得状态空间方程为:
(8)
根据文献[8]可确定下列自适应律:
(9)
式中,ΓP和ΓU的取值具有一定的随机性,可通过实验确定[9]。考虑到ΓP和ΓU取值的随机性,可将ΓPBsT和ΓUBsTP分别等价为任意值kp和ku。因此,本文收放卷系统模型参考自适应控制器的自适应律(一阶系统,而非矩阵形式)为:
(10)
kp和ku为任意正数,可根据实验确定。图8所示为基于模型参考自适应算法的收放卷系统张力控制器的框图。

图8 基于模型参考自适应算法的收放卷系统张力控制器框图
3 实验、仿真与应用
3.1 PID控制器实验
将以PID算法设计的速度控制器和张力控制器应用于收放卷系统,进行实验。图9所示为基于PID算法的收放卷系统运行实验结果。从图9可以看出,在多轴同步张力控制系统中, PID控制器启动阶段出现的超调较大,约为7.6%,升速阶段和减速阶段的张力波动过大,约为11%。
3.2 基于模型参考自适应算法的张力控制器仿真
针对式(10)的自适应律,在Simulink中可搭建基于模型参考自适应算法的张力控制器仿真系统(见图10)。
图11所示为基于模型参考自适应算法的张力控制器,从启动到稳定以及在20 s时突然升速而在40 s时减速的仿真结果。从图11可以看出,基于模型参考自适应算法的张力控制器可以较好地抵抗速度变化对其输出造成的干扰,具备较好的动态性能。
3.3 基于模型参考自适应算法的张力控制器应用
OPC(OLE for Process Control)通信协议是一种工业通信标准,解决了未公开通信协议的工控软件之间的通信难题。该协议包含OPC服务器和OPC客户端两部分,工业控制软件商提供工控软件的OPC服务器,而用户可通过OPC客户端软件与OPC服务器实现数据的交换[10]。
由于PLC编程软件不适合编写较为复杂的控制算法,而MATLAB软件具有可方便实现高级算法的优势,因此本文采用MATLAB软件编写自适应张力控制算法,并通过PLC实现实时控制。这就要求MATLAB与PLC两款软件以通信方式交换数据。本文参考文献[11],采用了OPC通信方式。图12所示为基于模型参考自适应算法的张力控制器OPC通信集成系统。在该集成系统中,MATLAB作为OPC客户端软件,Kepware作为OPC服务器软件。在Kepware软件中建立需要读写的PLC变量,在MATLAB软件中编写自适应律并选择合适的自适应律参数,即可实现MATLAB软件与PLC软件的数据实时交互。
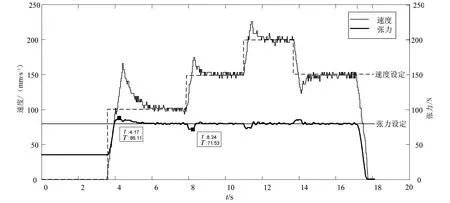
图9 基于PID算法的收放卷系统运行实验结果
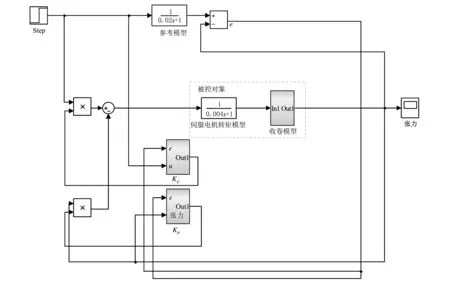
图10 基于模型参考自适应算法的张力控制器仿真系统
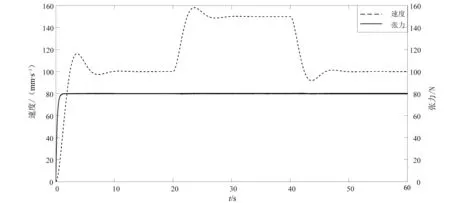
图11 基于模型参考自适应算法的张力控制器仿真结果
通过应用,采集运行数据,可得图13所示的基于模型参考自适应算法的张力控制器应用结果。
根据图13可计算出,系统启动阶段的超调量约为5.9%,加减速张力波动在7%左右。可进一步计算出如下结果:与PID控制器相比,基于模型参考自适应控制算法的张力控制器使收放卷系统的启动阶段张力超调量减小约1.7个百分点,升速减速阶段张力波动量减小约4个百分点。

图12 基于模型参考自适应算法的张力控制器OPC通信集成系统
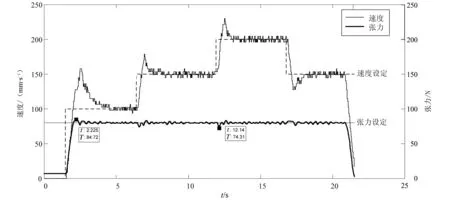
图13 基于模型参考自适应算法的张力控制器应用结果
4 结语
本文利用动力学建模方法建立系统的数学模型,根据该模型设计模型参考自适应张力控制器,并将该控制器应用于收放卷系统。通过MATLAB仿真可知,该控制器具有良好的动态性能和抗干扰性。从应用该控制器的收放卷系统运行数据可看出,该控制器较PID控制器减小了收放卷系统的张力超调量(约为1.7个百分点)和升速减速阶段的张力波动量(约为4个百分点)。

