局域共振型周期双层板简化模型带隙特性研究*
钱登辉, 史治宇
(1.苏州科技大学土木工程学院 苏州,215011) (2.南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)
引 言
在工程中许多领域,不同类型的板壳被用于外壳结构[1-2]。双层板结构具有许多单板结构所不具备的性能。外壳结构在振动传播过程中经常作为传播介质且不断向外辐射噪声。近年来,声子晶体概念主要研究大多集中在带隙计算方法和特性方面。带隙形成的机理常见的有Bragg散射机理[3-6]和局域共振机理[7-10]。两种机理最大区别在于局域共振带隙所在频域数量级要比Bragg散射带隙所在频域的数量级小得多,这就意味着基于局域共振机理构成的声子晶体可以用来控制更加低频的振动和噪声。因此,将传统局域共振性声子晶体的设计思路引入到板壳结构中,将为低频段的振动和噪声控制起到积极的作用[11-14]。
目前,局域共振性声子晶体单板结构已经获得了一定的研究。针对结构构造的不同,大致分为填充性和贴附型[15]两类。对于填充型声子晶体单板,文献[16-17]分别构造了二元和三元结构,应用平面波展开法研究了相应特性。Oudich等[18]应用有限元法研究了二元和三元贴附型声子晶体单板的带隙特性。Xiao等[17]通过在薄板上周期贴附弹簧质量块,构造贴附型结构的简化模型,并研究了其弯曲带隙特性。Qian等[19]研究了复合型局域共振声子晶体单板结构弯曲振动的传播特性。
基于单板研究现状,笔者构造了复合型局域共振声子晶体双层板结构,研究了其带隙特性。针对“弹簧-质量块”和“弹簧-扭簧-质量块”两种简化模型,通过将传统平面波展开法延伸到该结构,从是否考虑黏性的角度,分别对其带隙形成机理和调节规律进行了研究。
1 模型以及公式化


图1 结构模型Fig.1 Models of structures
假设双层板简化模型的上下板厚度均满足薄板要求,且只考虑质量块绕y轴的扭转而忽略绕x轴的转动,故认为上下板完全一致。根据薄板弯曲理论并参照对应的单板简化模型[19],图1(a)所示的简化模型的弯曲振动方程为
(1)
(2)
(3)
其中:W1(r)和W2(r)分别为下板和上板的挠度;WR(R)为质量块沿z向的位移;θR(R)为质量块绕y轴的扭转角度;ρ(r)为板的密度;h(r)为板的厚度;D(r)=E(r)h(r)3/12(1-μ(r)2)为板的弯曲刚度;E(r)为弹性模量;μ(r)为泊松比。
由于板由两种材料构成,硬材料和软材料的密度、弯曲刚度、弹性模量、泊松比分别用ρ1,D1,E1,μ1和ρ2,D2,E2,μ2表示。对于共振单元简化模型,各参数分别为弹簧刚度kF、质量块质量mR、扭簧刚度kM以及质量块转动惯量JR。此外,软材料的半径为Rs,晶格常数为a。
令α(r)=ρ(r)h(r),β(r)=D(r)μ(r),γ(r)=D(r)(1-μ(r)),则式(1)可简化为
(4)
由于结构在x和y方向的周期性,α(r),β(r),γ(r)和D(r)均可在空间域进行傅里叶级数展开
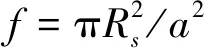
由于软材料是圆柱形的,所以ψ(g)=2fJ1(gRS)/(gRS)。其中:J1为一阶第1类Bessel函数;g为倒格矢G的模。
根据Bloch定理和结构周期性,位移场W1(r)和W2(r)可表示为
(7)
其中:k=(kx,ky)为不可约布里渊区边界上的二维Bloch波矢;G′为倒格矢。
由周期性和Bloch定理得到
(8)
根据狄拉克函数的特性,得到
(9)

由式(7)可以得到
(10)
将式(5)~(10)代入式(4),得到
(11)
若取倒格矢的个数为N,则式(11)矩阵化为
(12)
其中
UGij=SAGij+SBGij+SCGij+SDGij+SEGij
(13)
(14)
(15)
CGij=2(k+Gi)x(k+Gi)y×
γ(Gi-Gj)(k+Gj)x(k+Gj)y
(16)
(17)
(18)
FGij=α(Gi-Gj)
(19)
(20)
(21)
(22)
SG=
(23)
式(12)即为关于ω2的典型广义特征值问题。对于每一给定的波矢k,通过求解特征值可得到相应的一系列特征频率。通过所有的不可约Brillouin区边界上的波矢,得到该复合型局域共振声子晶体双层板简化模型的弯曲振动能带结构。表1为笔者计算用到的材料参数和几何参数。
表1 计算所用到的材料和几何参数
Tab.1 Materials′ and geometrical parameters used in calculations

参数数值参数数值E1/GPaμ1ρ1/(kg·m-3)E2/GPaμ2ρ2/(kg·m-3)kF/(N·m-1)77.60.352 7301.18×10-40.4691 3004×105mR/kgkM/(N·m2)JR/(kg·m2)a/mh/mRs/m0.11000.010.10.0024×10-6
2 数值结果和分析
2.1 “弹簧-质量块”贴附型局域共振声子晶体双层板简化模型
对于图1所示的复合型局域共振声子晶体双层板简化模型,若双层板只由一种硬材料构成,且共振单元为弹簧振子,扭簧忽略不计,则该模型可以简化为“弹簧-质量块”贴附型局域共振声子晶体双层板简化模型。
式(6)可以简化为
(24)
将式(24)代入式(14)~(19),可以简化为
将式(25)~(30)代入式(13),则
(31)
由于共振单元只为弹簧振子,则与扭簧相关的项应消除掉。于是,式(12)可化为
(32)
图2为“弹簧-质量块”贴附型局域共振声子晶体双层板简化模型的能带结构图。这里,平面波数取N=(5×2+1)2个。可以看出,能带结构在低频段(330~382 Hz)打开了一条完整的带隙。对于该双层板模型的带隙特性研究,文献[20]已经进行了详细研究。不同的是,该文献应用的是有限元法,但两种方法在处理该结构时均具有很高的精度,误差极小。总的来讲,通过研究分析表明,双层板结构具备的低频带隙性能优于单板结构。
为了描述方便,能带用符号G*表示,能带上的临界频率用符号F*表示。

图2 “弹簧-质量块”双层板简化模型能带结构Fig.2 Band structure of “spring-mass” simplified model of double panel structure
2.2 “弹簧-扭簧-质量块”贴附型局域共振声子晶体双层板简化模型
当考虑扭簧的作用时,采用式(12)对该简化模型的弯曲振动能带结构进行计算。由于板只由一种材料构成,所以方程里矩阵UG中的元素仍由式(31)求取。

图3 “弹簧-扭簧-质量块”双层板简化模型能带结构图Fig.3 Band structure of “spring-torsional spring-mass” simplified model of double panel structure
图3为“弹簧-扭簧-质量块”贴附型局域共振声子晶体双层板简化模型的弯曲振动能带结构。其中,平面波数取为N=(10×2+1)2个。将该能带结构与图2所示的同参数下不考虑扭簧作用的“弹簧-质量块”贴附型局域共振声子晶体双层板简化模型的弯曲振动能带结构进行对比发现,扭簧对图2中标示的能带G1,G2,1,G2,2,G4,1和G4,2均有影响,但对Bragg散射能带G3并无影响。另外,扭簧的添加使能带G1向下偏移,同时使得G2,1,G2,2,G4,1和G4,2向上偏移。因此,扭簧的增加不仅使带隙宽度增大,并且使带隙起始频率降低。
图4为扭簧刚度kM对带隙临界频率F1,F2,2,F3和带隙宽度Fw的影响关系。除了kM以外,计算用到的参数如表1所示,且kM的变化范围为0~200 N·m2。通过添加附加弹簧的方式可以使G2,1轻易移动到G2,2上方[20],所以这里不考虑kM对F2,1的影响。可以看出,随着kM的增大,F1减小,F2,2增大,F3保持不变。由于F2,2所在关系曲线一直在F3上方,所以Fw由起始频率F1和终止频率带隙F3决定,且一直在增大。因此,对于“弹簧-扭簧-质量块”贴附型局域共振声子晶体双层板简化模型,增加扭簧刚度可以对加宽带隙宽度和降低带隙起始频率同时起到积极作用。

图4 带隙临界频率及带隙宽度与扭簧刚度之间的关系Fig.4 The influences of torsional spring stiffness on critical frequencies and bandgap width
为了研究质量块转动惯量JR对“弹簧-扭簧-质量块”贴附型局域共振声子晶体双层板简化模型带隙的影响关系,计算了转动惯量为JR=0.1 kg·m2时该简化模型的弯曲振动能带结构,如图5所示。
计算用到的参数与图2对应的算例一致。对比图5和图2可以发现,能带结构是完全一致的,这说明对于“弹簧-扭簧-质量块”贴附型局域共振声子晶体双层板简化模型,转动惯量JR对其弯曲振动能带结构没有任何影响。

图5 转动惯量改变时“弹簧-扭簧-质量块”双层板简化模型能带结构图Fig.5 Band structure of “spring-torsional spring-mass” simplified model of double panel structure with rotational inertia changes
此外,通过与相应单板简化模型进行对比[19],扭簧的添加对单板和双层板的影响规律完全一致。
2.3 复合型局域共振声子晶体双层板简化模型
当“弹簧-扭簧-质量块”贴附型局域共振声子晶体双板简化模型的上下板由周期挖孔并填充软材料的复合板代替时,该简化模型则变为“弹簧-扭簧-质量块”复合型局域共振声子晶体双层板简化模型,如图1所示。此时,在计算其能带结构时,式(12)中的UG由式(14)~(18)求取。笔者从是否考虑复合板中软材料黏性这两个角度研究其带隙特性。为了计算的进度,笔者在计算该简化模型能带结构时均采用改进的平面波展开法[21]。
当不考虑复合板中的软材料黏性时,计算所得的“弹簧-扭簧-质量块”复合局域共振声子晶体双层板简化模型的弯曲振动能带结构如图6所示。在这里,由于复合板中存在两种材料,因此平面波数取N=(10×2+1)2个来增加计算精度。对比图2,3和图6可以发现, 复合板中的软材料与扭簧的作用类似,都使得能带G1向下偏移,并同时使得G2,1,G2,2,G4,1和G4,2向上移动。因此,复合板中软材料的添加同样对带隙宽度增大并且带隙起始频率降低起到促进作用。

图6 不考虑软材料黏性下复合型双层板简化模型能带结构图Fig.6 Band structure of simplified model of composite double panel structure with the viscidity of soft material not considered
图7为复合板软材料半径Rs对带隙临界频率F1,F2,2,F3和带隙宽度Fw的影响关系。除了Rs,计算用到的参数如表1所示,Rs的变化范围为1×10-6~5×10-6m。由于F2,1可以通过添加附加弹簧的方式增大到F2,2上方,因此无需考虑对F2,1的影响。可以看出,随着Rs的增大,F1减小而F2,2增大,且F3保持不变。F2,2所在曲线一直在F3上方,带隙宽度Fw由起始频率F1和终止频率F3决定,且一直保持增长。因此,对于该复合型局域共振声子晶体双层板简化模型,通过引入和调节复合板软材料的半径,不仅可以使所得能带结构的带隙宽度变宽,还能同时降低带隙的起始频率。
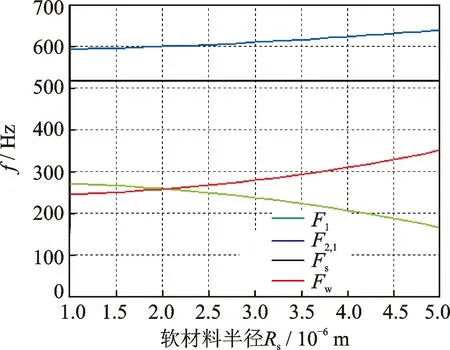
图7 带隙临界频率及带隙宽度与复合板软材料半径之间的关系Fig.7 The influences of soft material radius in composite plates on critical frequencies and bandgap width
当考虑复合板软材料的黏性作用时,在频域内,软材料的各模量与频率相关。式(12)的特征值问题需要通过迭代过程求解[19]。

图8 初始-终止值比对带隙的影响Fig.8 Influences of initial-final value ratio on band gap
图8(a)为软材料松弛时间为τ=3×10-5s,初始-终止值比α分别取1.5,2.0和2.5时的“弹簧-扭簧-质量块”复合型局域共振声子晶体双层板简化模型的弯曲振动能带结构图。其中,平面波数取N=(10×2+1)2个。可以看出,α对能带G1,G2,1,G2,2,G4,1和G4,2均有影响。为了进一步说明该影响规律,作出了带隙临界频率F1,F2,2,F3和带隙宽度Fw随α的变化曲线,如图8(b)所示。可见,随着α的增大,起始频率F1减小,F2,2增大,而F3保持不变。由于F2,2所在曲线一直在F3上方,因此带隙宽度由F1和F3决定,且一直增大。由此可见,通过增大黏弹性软材料的初始-终止值比,对增大该声子晶体双层板简化模型的带隙宽度和降低其起始频率具有积极作用。
图9(a)为软材料初始-终止值比为α=2.0,松弛时间τ分别取3×10-5s,1×10-4s,3×10-4s时的弯曲振动能带结构图。其中,平面波数取N=(10×2+1)2个。可以看出,τ对能带结构有一定的影响,但影响不大。带隙临界频率F1,F2,2,F3和带隙宽度Fw随τ的变化曲线图如图9(b)所示。可以看出,随着τ的增大,起始频率F1增大而F2,2减小,且F3保持不变。由于F2,2的变化曲线一直在在F3的上方,所以带隙宽度Fw由起始频率F1和终止频率F3决定,且随着τ的增大而减小。总的来说,对于该声子晶体结构,τ对各临界频率的影响范围远不及α。但是,通过减小黏弹性软材料的松弛时间对增大该声子晶体简化模型的带隙宽度和降低其起始频率还是具有一定的促进作用。
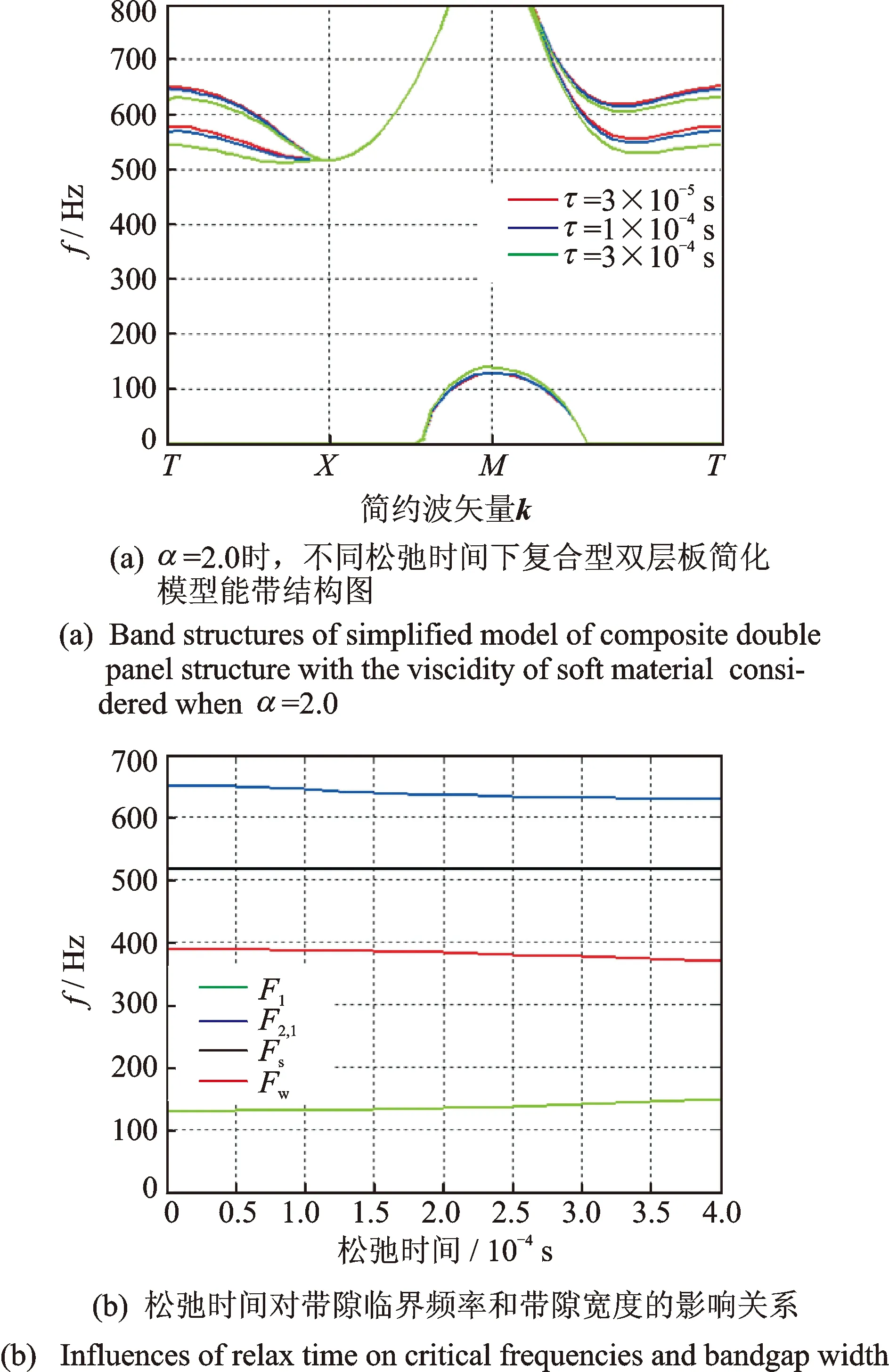
图9 松弛时间对带隙的影响Fig.9 Influences of relax time on band gap
3 结 论
1) 在低频段,能带结构可以打开一条完整的带隙。扭簧对带隙有明显的影响,通过增加扭簧刚度不仅可以增大带隙宽度,更能降低带隙的起始频率,但改变转动惯量对能带结构没有任何影响。
2) 软材料的添加对能带结构的影响与扭簧的影响相似,通过增大软材料的半径,不仅使能带结构带隙变宽,还能降低带隙的起始频率。当考虑软材料黏性作用时,通过增大黏弹性软材料的初始-终止值比或者减小松弛时间,可以增大该双层板简化模型能带结构的带隙宽度及降低其起始频率。

