超声波固态耦合声特性研究*

唐东林， 胡 琳， 汤炎锦， 吴薇萍， 袁 波

(1.西南石油大学石油天然气装备教育部重点实验室 成都，610500) (2.西南石油大学机电工程学院 成都，610500)

引 言

传统的超声波检测技术必须在超声探头与工件之间的界面涂抹液体耦合剂以实现良好的声耦合，但液体耦合剂无法用于不能润湿的精密构件检测。另外，对大型、特大型设备进行超声自动化检测携带大量的液体耦合剂，将产生检测设备庞杂、检测费用高等缺点。超声波固态耦合用固体耦合材料取代液体耦合剂，既不会润湿被检材料又可重复使用，彻底解决了上述难题，同时运用在轮式超声波换能器中，能够实现自动化检测[1-3]。固体耦合剂通常选择柔性聚合物，例如，亲水性聚合物、橡胶及特制固体耦合剂[4-8]等具有良好声耦合性能的材料。

表征声耦合性能的重要参数是超声波在界面的反射率，反射率越大，耦合性能越差。对超声波固态耦合而言，界面反射率大小不仅受固态耦合剂与被检材料之间的声阻抗影响，界面粗糙度和耦合压力也是十分重要的影响因素。固体耦合材料与被检工件表面直接接触，在压力作用下形成耦合界面，超声波通过界面传入工件实现检测。受界面粗糙度的影响，若所施压力不足以形成理想耦合界面，则界面内将残存少量空气。空气的声阻抗远低于界面声阻抗，将使耦合阻抗严重失配而达不到理想的传声效果。针对这一现象，Ramesh等[9]研究了超声波反射幅值与表面粗糙度之间的关系并进行了实验验证。对于粗糙接触界面状态，可以通过接触刚度来表征。王世军等[10]对超声波测量机械接触刚度的研究现状进行了分析，表明接触表面的反射系数是接触刚度的函数。这些研究都明确提出了界面粗糙度和所施压力对超声波干耦合界面声学特性的影响。

理论上提出的模型主要有低频弹簧模型[11]、Haines的粗糙界面统计模型以及数值接触模型与裂纹模型[12]等。这些模型研究了固体间界面声反射系数与施加的表面接触压力或表面粗糙度之间的关系，粗糙界面统计模型考虑独立的弹性和弹塑性，采用实际接触面积的弹簧模型来计算反射系数。数值接触模型给出了负载与界面几何形状的关系，同时将低频弹簧中不完全接触的界面看作一个裂缝，建立了中心裂纹和双边缘裂纹模型，用断裂力学分析裂纹的刚度，作为不完全接触的等效刚度，但橡胶的动态弹性模量会影响测量值与计算出的反射系数的一致性。

数值接触模型和裂纹模型能较好地描述超声干耦合的声学特性，但该模型只对界面粗糙度和界面施力对反射系数的影响进行了单独变量的实验分析，缺乏具体的相关性理论模型，理论与实验值只在一定区域吻合得很好[13]。

为了研究超声波界面反射系数、表面粗糙度和界面压力之间的关系，笔者建立了基于界面总载荷量和粗糙度的干耦合模型。通过该模型，建立了界面粗糙度与界面施压对界面接触刚度的表达式，并用于计算反射系数。将所提出的模型与文献[12]的模型进行对比分析，发现提出模型的预测值有更宽的有效适用范围，更符合实验结果。通过设计的轮式干耦合探头实验，验证了所提出模型对不同界面粗糙度和作用力下的适应性。结果表明，该模型能正确描述固态耦合剂与被检材料界面的声耦合特性，对于基于超声波干耦合的超声自动检测技术具有重要意义。

1 基于界面刚度的干耦合模型

当两个接触面上的应力和位移分量具有连续性时，两种材料处于理想的协调状态，这种边界条件代表两个接触面处于完全接触，符合声波小振幅的线性声学理论假设。当超声波正入射时，其反射系数计算公式为

(1)

其中：Z1,Z2，为两接触材料的特性阻抗。

对于干耦合而言，当界面压力过小时，实际反射系数会近似为1，当压力增大到某一状态时，反射系数会减小至式(1)所计算出的理论值，即干耦合材料与被检工件界面接近完全接触。针对这一不符合经典反射系数计算公式的现象，文献[14]用准静态的均布弹簧模型研究了超声波在接触界面上的反射情况，通过分布的无质量弹簧传递载荷，两个弹性体之间的耦合强度用弹簧刚度表示。因此，实际粗糙界面状态可等效成接触刚度系数为k的弹簧模型[15]，界面耦合特性可用准静态的均布弹簧模型表示，其反射系数的计算公式[14]为

(2)

k值不能直接从材料属性中获得，需建立新的干耦合界面模型，推导出界面等效刚度k的计算方法，从而得到准确的反射系数计算公式。

2 基于界面总载荷量和粗糙度的干耦合界面模型

如图1所示，当两个粗糙接触面在受压状态下相接触时，两界面可转换为一个刚性光滑表面和另一个当量粗糙表面的接触。图1中：h为两表面间的距离；z为粗糙轮廓高度。当z>h时，界面变形δ=z-h，则该模型中界面等效刚度k、界面总载量W和界面变形δ之间满足

(3)

可以看出，要得到等效刚度k，需先求得产生δ变形的界面总载量W。

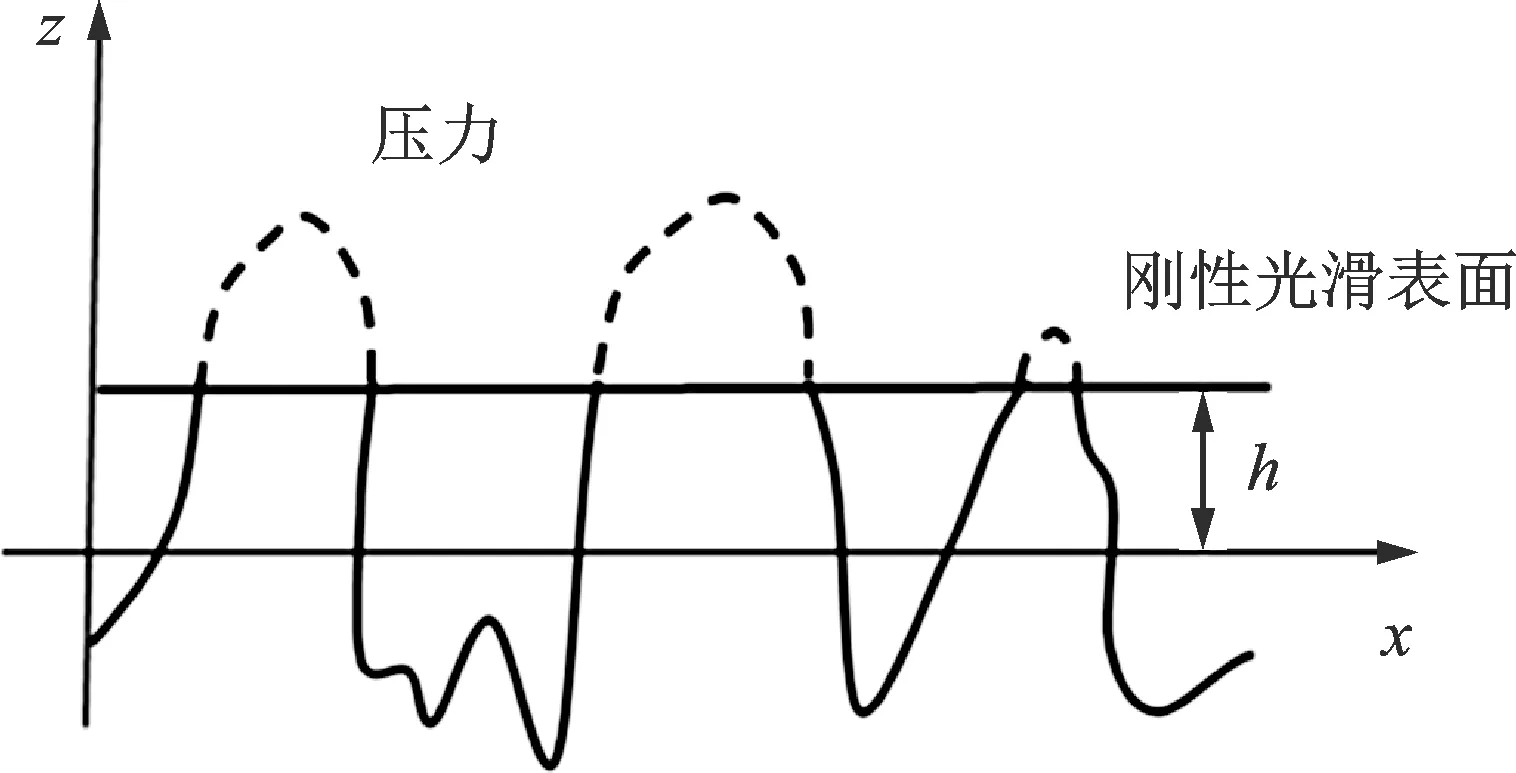
图1 当量粗糙度表面与刚性光滑表面的接触Fig.1 Contact between an equivalent roughness surface and a rigid smooth surface

2.1 界面总载量

在界面总载量W作用下，发生接触的粗糙峰高度符合概率密度函数

(4)

若粗糙界面凸出的峰点总数为m，则参与接触峰的个数n可以通过概率计算得到

(5)

各个接触峰点的法向变形量为z-h。实际接触区域是以a为半径的圆，R为假设粗糙峰为均匀圆柱体的曲率半径，实际接触面积根据赫兹接触理论可知

(6)

(7)

(8)

从以上关系可得a2=R(z-h)。实际接触面积A为

A=nπa2=nπR(z-h)=

(9)

总载量W为

(10)

其中：E*为当量弹性模量；E为随机粗糙峰当量弹性模量。

2.2 界面等效刚度

在所提出的模型中，实际两接触界面的轮廓高度服从高斯分布。在高斯分布中，z值较大的峰值部分近似于指数型分布。令φ(z)=exp((-z)/σ)，代入式(10)可得

(11)

变形δ与轮廓高度的变量-h相差一个常数，故界面接触刚度可表示为

(12)

2.3 反射系数

将式(12)代入式(2)，得到反射系数为

(13)

其中:ω=2πf。

(14)

由式(14)可知，当使用一定频率的超声波探头检测被检工件时，由界面总载荷量和粗糙度即可得到反射系数R12。

3 干耦合模型的仿真分析

对在干耦合非理想界面模型下声波与界面的相互作用进行数值仿真。仿真实验使用铝板与硅胶作为两界面的材料,根据建立的干耦合非理想界面模型，可以将界面接触刚度转化为表面粗糙度与界面总载荷之间的关系，由式(14)直接通过测量值得到干耦合的反射系数。当界面两侧介质声阻抗(Z1，Z2)固定、探头频率为2.5MHz时，数值计算所提出模型的反射系数、界面粗糙度与界面总载荷之间的关系曲线如图2所示。

图2 界面粗糙度、反射系数与界面总载荷关系曲线Fig.2 Reflection coefficient variation with total interface load for different surface roughnesses

由图2可知，三者之间呈非线性关系，无论界面粗糙度为多少，随着界面总载荷增加，反射系数均逐渐减小，这说明在超声干耦合技术中对界面施加载荷有利于声波在界面的传播。可以看出，当施加恒定的接触压力时，界面粗糙度越小，反射系数越小，耦合效果越好。这说明通过调整界面施加负载值的大小，可以使不同粗糙度界面达到良好的声耦合效果。

对干耦合模型分析可知，推导结果中反射系数与频率的关系被引入。当频率趋于0(静态情况下)，反射系数近似为完全接触界面时的数值。随着频率的增加，反射系数会逐渐趋向于1。当选定界面粗糙度为2.285时，反射系数随频率变化的仿真结果如图3所示。

图3 不同载荷下，反射系数随频率的变化Fig.3 Reflection coefficient variation with frequency under different loads

如图3所示，当超声波在传播过程中遇到界面时，低频超声要达到更好耦合效果所需要的界面载荷更小，更易于实现干耦合，频率越高，越难以达到较好的耦合效果。从图4可以看出，固定负载为6MPa时，粗糙度越小，对频率变化的适应性越强，高频超声对粗糙度更敏感。所以高频超声在采用固体耦合剂进行探伤时对检测表面状况与施压条件要求更高。

图4 不同界面粗糙度下，反射系数随频率的变化Fig.4 Reflection coefficient variation with frequency under different Interface roughness

4 模型对比与验证

4.1 数值接触模型与裂纹模型的界面刚度

基于低频弹簧模型的数值接触模型研究了反射系数与界面接触几何形状的关系。数值接触模型通过在不同的压力下，界面的几何形状变化以确定界面弹簧刚度(界面等效刚度)，从而确定反射系数。通过压力Δp以及产生的界面位移Δδ1，得到界面刚度

(15)

(16)

在低频弹簧模型中因不完全接触的界面细长，也可以用裂缝来近似表示。建立中心裂纹和双边缘裂纹模型，用断裂力学分析裂纹的刚度，作为不完全接触的等效刚度。裂纹周围的应力场和裂缝间位移与力的关系已知，刚度从断裂力学手册中获得。低接触百分比时，二维等效为边缘裂纹模型。高接触百分比时，二维等效为中心裂纹模型。选择单元界面的裂纹模型类型后，再计算整体界面刚度。

4.2 模型的实验与仿真分析

为验证所建立干耦合模型的正确性，同时与另两种模型对比，设计了如图5，6所示的轮式探头为实验平台。信号激发电路发射3个周期频率为2.5MHz的脉冲，激励轮式换能器产生超声波并垂直入射至接触界面，回波信号由示波器接收显示。

图5 轮式固体耦合换能器实验平台意示图Fig.5 Experimental platform of wheel solid coupling transducer

图6 轮式固体耦合换能器实验平台实物图Fig.6 Experimental platform of wheel solid coupling transducer

采用固体耦合剂作为耦合介质对粗糙度为0.428的铝板进行检测实验，通过测量入射声压与透射声压计算出反射系数的实验值。图7为相同条件下实验所得反射系数与3种模型预测值随负载变化的关系曲线。可以看出，当负载在1MPa～2MPa之间变化时，3种模型均出现明显误差，而提出模型的误差最小。数值接触模型的最大相对误差为5.60%，裂纹模型的最大相对误差为4.81%，提出模型的最大相对误差为3.56%。当负载超过2MPa时，耦合效果达到最佳(具有较大工程意义)，基于界面总载荷与粗糙度的所提出模型更准确地描述了界面接触特性。数值接触模型与裂纹模型在建立时进行了较多简化，缺乏对粗糙界面更具体的形貌分析。笔者所提出模型采用高斯分布描述粗糙界面，与实际界面的粗糙轮廓高度更接近，因此该模型具有更好的科学性与实用价值。

图7 实验值与3种模型理论值随负载变化的对比Fig.7 Comparison between the experimental values and the theoretical values of the three models with the change of load

为验证模型的有效性，在多组表面粗糙度不同的铝板上重复实验。通过对探头轮进行施压形成粗糙接触界面，测试了铝板表面粗糙度在不同压力下与反射系数的关系，将实验与笔者所推导的模型仿真进行对比分析。图8为0.066，0.428，1.609和4.529这4种规格粗糙度铝板的实验与仿真结果。

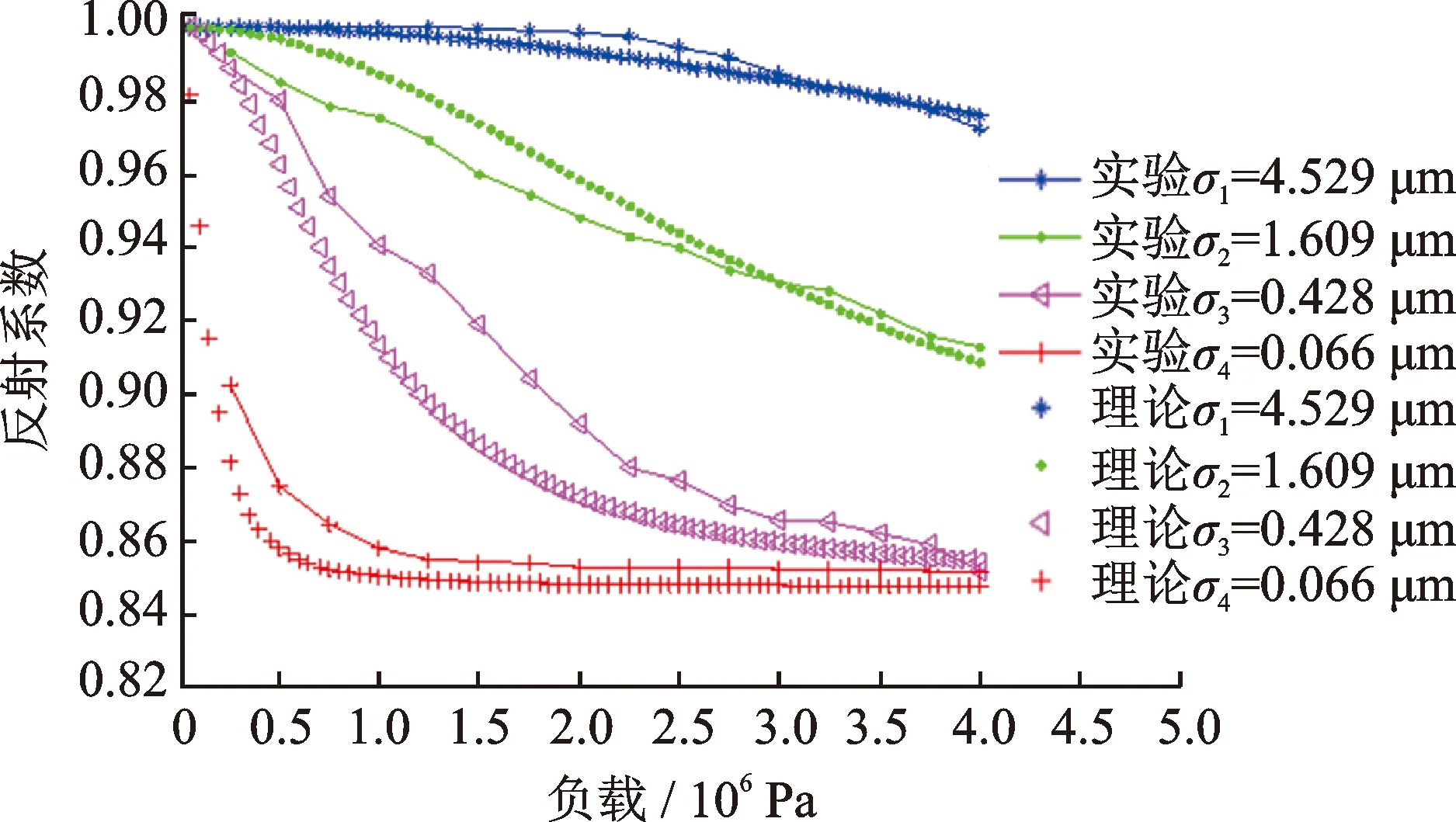
图8 模型理论值与实验值的比较Fig.8 Comparison of model theoretical values and experimental values

图8表明，对于表面粗糙度不同的铝板，其声反射系数与压力关系曲线的实验数据与理论计算具有良好的一致性，满足对检测结果进行分析的需求，所提出模型可准确描述粗糙接触界面反射系数变化规律。通过建立反射系数随界面压力与粗糙度变化关系模型，可在工程实践中预测已知表面状态下要达到一定耦合效果所需的压力。

5 结束语

将干耦合界面特性通过粗糙界面模型与准静态弹簧模型进行量化，用界面粗糙度与界面总载荷可直接得到声压反射系数。相较数值接触模型与裂纹模型，新的干耦合界面模型能够很好地描述粗糙接触对实验测量结果造成的影响，最大相对误差为3.56%，可为粗糙接触界面的干耦合超声检测的参数评价提供理论依据。

对于非光滑界面干耦合超声检测，反射系数会受到压力与材料表面状态的影响。由于固体耦合介质与实际粗糙表面的界面接触时力学特性复杂，而理论模型是在一定假设条件下建立起来的，因此模型与实验测试的结果有一定的差距，需要考虑更多的影响参数，拟合出更接近实际情况的模型。