伸缩缝结构的环境振动监测与动力特性识别*

刘 佩, 朱海鑫, 连鹏宇, 杨维国

(北京交通大学土木建筑工程学院 北京， 100044)

引 言

设置变形缝的建筑结构在实际工程中广泛存在，世界范围内的地震破坏调查发现，设置变形缝结构间的碰撞频繁出现，给人们的生命财产带来巨大损失[1-4]，而变形缝两侧相邻结构的动力特性是影响其在地震作用下碰撞响应的决定性因素。

目前，对设置变形缝结构进行设计和分析时，一般都忽略变形缝的影响，假定缝两侧结构相互独立；但结构建成后，为满足其使用功能，需对变形缝进行塞缝和盖缝处理。根据变形缝的不同施工质量，现有设置变形缝结构可分为两类：a.依据设计要求进行塞缝和盖缝处理；b.施工时变形缝内采用刚性填充物代替柔性填充物，或由于二次装修导致楼板面层和吊顶直接盖缝而不中断。前期研究结果表明，按设计要求施工的变形缝不会改变相邻结构各自的动力特性，但会引起相邻结构的相互作用模态[5-6]；变形缝内填刚性物质会造成相邻结构动力特性的改变[7]。使用年限较长的设置变形缝结构经常会在二次装修时为了美观而使楼板面层在变形缝处不中断，进而改变了相邻结构的边界条件，因此需对此类结构进行研究，为设置变形缝结构的现状评估及抗震设计提供一定的依据和建议。

测试环境激励下的结构振动响应在实际原型结构工作状态下即可进行，不需要在实验室搭建结构模型和激振设备，因而近年来受到广泛关注，被成功用于钢筋混凝土建筑结构的动力特性检测[6, 8-10]。基于结构振动响应测试数据，结合结构模态参数识别方法[11-12]，得到实际结构的模态参数，进而对结构的状态进行评估。因此，将环境振动测试用于确定设置变形缝结构的相互作用程度，对研究其动力特性是有效的。通过长期振动监测可以确定结构各阶段的健康状况，并可以分析环境因素对结构动力特性的影响[13-14]。伸缩缝的主要作用是防止由于建筑物平面尺寸过长在温度变化时结构产生裂缝，温度变化对设置伸缩缝结构动力特性的影响不可忽略，可利用长期振动监测将此影响定量化。

笔者首先对某设置伸缩缝的框架剪力墙结构进行了环境振动测试和模态参数识别，评估了伸缩缝所起的实际作用；然后，对该相邻结构进行了长期振动监测，分析了伸缩缝随温度变化对结构动力特性的影响；最后，提出了考虑不同温度下伸缩缝作用的所测相邻结构的有限元建模方法，为同类结构的动力特性分析提供参考。

1 伸缩缝结构测试

测试的伸缩缝钢筋混凝土框架剪力墙结构如图1所示。该建筑地上为8层，总高为29.3m，4层平面布置如图2所示。伸缩缝将该建筑分为东侧结构(地下为1层，长为48m)和西侧结构(长为25.5m)。伸缩缝设计净宽度为170mm。外墙伸缩缝处采用铁皮盖缝，内墙伸缩缝处采用木板盖缝。1～5层楼板伸缩缝处采用水磨石面层盖缝。由于二次装修，6～8层楼板伸缩缝处地砖面层和各层吊顶伸缩缝处直接盖缝无中断，如图3所示。屋面伸缩缝两侧砌筑砌体矮墙并利用钢筋混凝土板盖缝。

图1 所测设置伸缩缝(矩形框处)的相邻结构Fig.1 Studiedadjacent structures with an expansion joint

图2 四层结构平面布置图(单位：mm)Fig.2 Structural layout of the fourth floor (unit: mm)

图3 楼内伸缩缝Fig.3 Expansion joint within the building

2 环境振动测试方案

2016年6月在该楼缝两侧结构的楼梯间及屋顶分别进行了环境振动测试，为避免人员活动干扰，楼梯间测试的时段选在夜间进行。

1) 工况1在西侧楼梯间4，6，7，8层同时布置朝东(x向)和朝北(y向)的水平向加速度传感器(共8个，位于图2中W4处)；工况2在西侧楼梯间2，3，4，5层同时布置朝东和朝北的加速度传感器；各层传感器在竖向保持在一条直线上。

2) 工况3和工况4：测试在东侧楼梯间(图2中E4处)进行，方案分别同工况1和工况2。

3) 工况5和工况6：测试在中部楼梯间(图2中EM4处)进行，方案分别同工况1和工况2。

4) 工况7和工况8：分别在西侧结构和东侧结构屋顶4个角点(位置同图2中WA-WD点及EA-ED点)布置朝东和朝北的加速度传感器。

5) 工况9：在屋顶伸缩缝两侧4个角点(位置同图2中EC，ED，WA和WB点)布置朝东和朝北的加速度传感器，测试照片如图4所示。

图4 屋顶部分测点Fig.4 Sensors on the roof

各工况测试时长均为20min，采样频率为512Hz，利用北京东方振动和噪声技术研究所的8通道INV3018CT和中国地震局工程力学研究所的水平向941B型超低频加速度传感器进行数据采集。

3 模态参数识别结果分析

3.1 加速度功率谱和奇异值谱曲线

测试得到各通道的加速度数据，计算得到各工况的功率谱(power spectral density spectra，简称PSD)和最大奇异值谱(singular value spectra，简称SV)如图5所示。计算PSD和SV时，快速傅里叶变换采样点数为8 192，加汉明窗，窗长同采样点数，窗长重叠部分为25%。由图5可以看出，各工况均有显著的对应结构模态的峰值，且峰值频率基本相等。

图5 各工况功率谱及最大奇异值谱Fig.5 PSD and SV spectra corresponding to the largest singular values for the four setups

3.2 自振频率和阻尼比识别结果

采用改进的频域分解法[5]进行结构模态参数识别，其基本思想为利用奇异值谱的峰值识别得到结构的振型，通过最小二乘技术识别结构的自振频率和阻尼比。

识别得到的各阶自振频率和阻尼比(括号内数值)如表1所示。可以看出，缝两侧结构在各工况下识别得到的同阶自振频率基本相等。另外，不同工况同阶自振频率非常接近，而同阶阻尼比离散性较大，表明自振频率具有较高的识别精度。由于结构复杂的阻尼机制，阻尼比的识别精度相对较差。

3.3 振型识别结果

根据东侧和中部楼梯间的测试数据识别得到的四阶振型如图6所示。可以看出：东侧楼梯间第1阶振型为y向(短轴向)一阶弯曲振型，第2阶振型为x向(长轴向)一阶弯曲振型，第3阶振型为扭转振型且y向振动分量较大，第4阶振型为二阶扭转振型。中部楼梯间前两阶振型形式与东侧楼梯间相同，第3阶振型为y向一阶弯曲振型(此阶模态整体结构为扭转，但在中部楼梯间处x向分量很小)，第4阶振型为y向二阶弯曲振型。西侧楼梯间的各阶振型形式与东侧楼梯间相同。根据屋顶的测试数据识别得到的四阶振型如图7所示。可以看出：缝两侧结构同步振动；第1阶振型为y向平动，第2阶振型为x向平动，第3阶振型为扭转振型且中部y向振动分量较大，第4阶振型为x向反向平动耦合东侧结构的y向平动。

3.4 相干函数计算结果

为进一步明确东侧和西侧结构的动力相互作用程度，利用屋面伸缩缝两侧的同步测点数据计算其在各频率f处的相干函数C(f)

(1)

其中：PEE(f)为缝东侧测点数据在频率f处的自功率谱密度；PWW(f)为缝西侧测点数据在频率f的自功率谱密度；PEW(f)为缝两侧测点数据在频率f的互功率谱密度，PEW处于0～1之间，越接近于1，则缝两侧测点数据的相关性越大[15]。

表1 识别得到的自振频率及阻尼比Tab.1 Identified natural frequencies and damping ratios

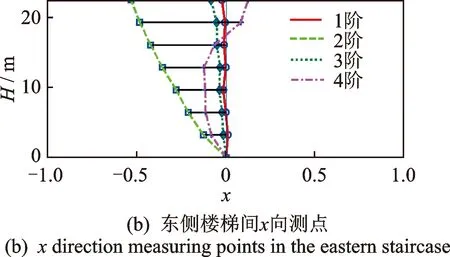
图6 楼梯间测点识别得到的四阶振型Fig.6 Mode shapes of the four modes identified from the data measured in the staircases

图7 屋面测点识别得到的四阶振型Fig.7 Mode shapes of the four modes identified from the data measured on the roof

屋面伸缩缝两侧测点WA与ED(图2)的y向和x向加速度数据的相干函数(magnitude-squared coherence，简称MSC)曲线如图8所示，在结构各阶自振频率(屋面测点各工况平均值)处的MSC值如表2所示。

图8 测点WA与ED的相干函数Fig.8 Magnitude-squared coherences between the measured data from sensors at WA and ED

Tab.2 Magnitude-squared coherence values at the structural natural frequencies

各阶自振频率/Hzy向MSCx向MSC2.011.000.002.860.521.004.230.950.547.890.130.87

由图8和表2可以看出,伸缩缝两侧测点y向振动在2.01Hz(y向一阶平动振型)处完全相关(MSC=1.00)，x向振动在2.86Hz(x向一阶平动振型)处完全相关，在4.23Hz(一阶扭转振型)处y向振动的相关性(MSC=0.95)大于x向振动的相关性(MSC=0.54)，在7.89Hz(二阶扭转振型)处x向振动的相关性大于y向振动的相关性。

3.5 伸缩缝对所测相邻结构动力特性的影响

根据测试识别结果可以得到：缝两侧结构的功率谱密度曲线峰值频率相等，识别所得各阶自振频率相等，各阶振型形式相同，结构自振频率处缝两侧测点数据在该阶模态方向相关性极高，表明在环境微幅振动下缝两侧结构耦合为一个系统。由于缝两侧结构的设计并不相同，因此缝两侧结构通过伸缩缝处的盖缝措施形成一个系统，主要是由于楼板装修面层在缝处没有中断引起的。

针对本次测试，该结构系统的四阶自振频率平均值分别为2.01，2.77，4.22和7.77Hz；四阶阻尼比平均值分别为1.70%，3.45%，2.27%和2.48%。第1阶振型为y向一阶弯曲振型，第2阶振型为x向一阶弯曲振型，第3阶振型为一阶扭转振型且表现为系统两端扭转而中部沿y向平移，第4阶振型为二阶扭转振型。

4 长期振动监测

为了研究温度变化对所测设置伸缩缝结构动力特性的影响，2016年10月～2017年11月，每隔2周在伸缩缝两侧四层楼板同时布置测点进行振动监测(图9)，每次测试时长为20min。2017年11月24日晚11点～26日早6点，在伸缩缝两侧四层楼板同时布置测点进行振动监测，每隔20min采集一组数据，每组数据采集20min。东侧结构前三阶自振频率随温度的变化规律如图10所示，西侧结构变化规律相同。

图9 长期监测测点Fig.9 Sensors for long term monitoring

图10 东侧结构自振频率随温度的变化规律Fig.10 Trends of natural frequencies varying with the temperature for the eastern structure

由图10可以看出：结构的第1和第2阶自振频率随温度升高变化不大，而第3阶自振频率随温度升高增大较多，温度为30oC时，与温度为-1oC时相比，第3阶自振频率变化率为18%。由于结构系统的第1和第2阶模态为缝两侧结构整体的短轴向和长轴向平动模态，对温度变化不敏感；而第3阶模态为缝两侧结构的相向扭转模态，随着温度升高，缝两侧结构的相互作用增强，此阶自振频率增大。

如图10所示，对第3阶自振频率f3和温度T进行回归分析，所得回归方程为

f3=3.553+0.026T

(2)

式(2)表明第3阶自振频率随温度升高而线性递增。

为了区分温度和湿度对结构动力特性的影响，在2017年11月24日晚11点～26日早6点的东侧结构监测数据中(在此测试期间认为结构的荷载没有变化)挑选湿度差别较小的各组数据(湿度范围28.5%～32.3%)，其自振频率随温度的变化如图11(a)所示。可以看出,第3阶自振频率仍然表现为随温度升高而增大；挑选温度差别较小的各组数据(温度范围4.2oC ～5.4oC)，所得自振频率随湿度的变化如图11(b)所示。可以看出，第3阶自振频率不随湿度发生变化，上述现象与伸缩缝主要是防止由于温度变化使结构开裂的作用一致。

图11 东侧结构湿度接近时自振频率-温度关系与温度接近时自振频率-湿度关系Fig.11 Trends of natural frequencies varying with temperature for similar humidity and varying with humidity for similar temperatures for the eastern structure

5 有限元模态分析

5.1 考虑伸缩缝作用的结构有限元模态分析

根据设计图纸可知，所测结构的楼板、墙、梁和柱的混凝土强度等级为C30。剪力墙的厚度主要为200mm，楼板的厚度主要为110mm。框架柱的截面尺寸主要为600mm×600mm。外墙采用240mm厚盲孔砖，根据建筑结构荷载规范《GB50009-2012》，弹性模量为2.8GPa，质量密度为1 500kg/m3。内墙采用200mm厚加气混凝土砌块，弹性模量为2.3GPa，质量密度为825kg/m3。除首层和顶层略有不同外，其他各层的结构布置与图2中的四层结构布置相同。

利用SAP2000建立有限元模型进行模态分析，计算模型的基本假定为：a.楼板、墙、梁、柱处于线弹性；b.考虑东侧结构的地下室；c.考虑填充墙对结构抗侧刚度的影响；d.根据测试时的实际情况，在楼板上施加2.5kN/m2的均布荷载，并转化为质量考虑；e.考虑伸缩缝对两侧结构的连接作用，伸缩缝处盖板设计厚度为40mm，主体材料同楼板面层，采用同厚度的板连接两侧结构，弹性模量取20GPa。

梁和柱通过框架单元进行模拟；楼板、剪力墙、填充墙、缝处连接板和楼梯斜板均通过壳单元进行模拟。有限元模型结构系统的自振频率如表3所示，可以看出所得各阶自振频率与识别结果较为接近。

结构系统有限元模型所得振型如图12所示。可以看出模型各阶振型形式与识别所得振型形式相同。其中，中部楼梯间振型的识别结果与模型中部楼梯间各测点对应的前三阶振型的模态保证准则(modal assurance criterion,简称MAC)值分别为0.96，0.92和0.97，各值均接近1，表明各阶振型相关程度较高。

表3 有限元模型所得自振频率

Tab.3 Natural frequencies obtained from the finite element model of the structural systemHz

自振频率第1阶第2阶第3阶第4阶识别结果2.012.774.227.77结构系统模型2.082.824.237.21东侧独立结构模型2.032.562.677.25西侧独立结构模型2.333.173.487.84不考虑填充墙模型1.862.233.966.04

图12 结构系统有限元模型所得振型Fig.12 Mode shapes obtained from the finite element model of the structural system

5.2 模态分析结果的影响因素

5.2.1 不考虑伸缩缝的作用

假定缝两侧结构相互独立，所得东西两侧独立结构模型的各阶自振频率如表3所示，与识别结果偏差较大。结构系统模型的前两阶自振频率各自介于东侧和西侧独立结构模型的前两阶自振频率之间，其第3阶自振频率大于东侧和西侧独立结构模型的第3阶自振频率。

5.2.2 不考虑填充墙的作用

假定不直接考虑填充墙的作用，仅考虑结构模型的周期折减系数取0.9，所得各阶自振频率如表3所示，均小于识别值。此外，该有限元模型各阶振型与识别所得振型之间的MAC值仅为0.5左右，表明填充墙的存在不仅影响结构的自振频率，同时也会对结构的刚度分布即结构的振型产生显著影响。

5.3 伸缩缝对结构自振频率的影响

为分析伸缩缝对两侧结构的连接效果，改变模拟其作用的连接板的弹性模量，则结构各阶自振频率的变化规律如图13所示。可以看出，随着连接板弹性模量的增加，结构系统的前两阶自振频率基本不变，第3阶自振频率增大，与温度升高时测试识别所得结构各阶自振频率的变化规律一致。例如，伸缩缝处连接板弹性模量为5GPa和20GPa时的模型第3阶自振频率分别与温度为-1oC和30oC时识别值较为接近。

图13 伸缩缝处连接板弹性模量对结构自振频率的影响Fig.13 Effects of the elastic modulus of the slab across thejoint on the natural frequencies of the structural system

6 结 论

1) 通过对某设置伸缩缝的钢筋混凝土框架剪力墙结构进行环境振动测试和模态参数识别，研究了伸缩缝对实际建成后相邻结构动力特性的影响。结果表明，由于楼板装修面层直接盖缝等措施，使缝两侧结构形成了一个系统，缝两侧结构的各阶自振频率相等且振型形式相同，结构自振频率处缝两侧测点数据在该阶模态方向相关性极高。

2) 通过对该设置伸缩缝结构进行长期的振动监测，研究了温度变化对其动力特性的影响。结果表明，随着温度升高，第1阶和第2阶自振频率变化不大，第3阶自振频率线性递增，且测试温度接近时，各阶自振频率不随湿度不同发生变化。

3) 通过在伸缩缝处采用板连接两侧结构，提出了设置伸缩缝结构的有限元建模方法。结果表明，增加伸缩缝处连接板的弹性模量，第1阶和第2阶自振频率基本不变，第3阶自振频率增大，可模拟温度升高时识别频率的变化规律。

4) 对于类似本研究缝处未中断的设置伸缩缝结构，相邻结构出现相向扭转模态，该模态受温度影响显著，可利用一定弹性模量的板对缝处的连接作用进行模拟。对于其他设置伸缩缝结构，无论变形缝装置的形式和施工质量如何，均不同于设计时假定的相邻结构相互独立的边界条件，但可通过现场振动测试、模态参数识别和与独立结构有限元模态分析结果的对比，评估变形缝对结构动力特性的影响。

5) 建议在设计带伸缩缝结构时，除了建立缝两侧独立结构模型外，还应考虑伸缩缝的处理方式，建立存在相互作用的结构系统模型，以便考虑模型假定与实际造成的结构动力特性的差异。