深度学习LSTM模型的电离层总电子含量预报

吉长东，王 强，王贵朋，刘亚南

深度学习LSTM模型的电离层总电子含量预报

吉长东1，王 强1，王贵朋2，刘亚南1

（1. 辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2. 日照市城乡建设勘察测绘院有限公司，山东 日照 276800）

针对TEC时间序列高噪声、非线性和非平稳的动态序列的特性，基于分解-预测-重构的思想，运用总体经验模态分解和深度学习长短期记忆神经网络，构建了EEMD-LSTM预测模型。同时，以测试集上预测结果的均方根误差最小为目标，运用多层网格搜索算法对EMD-LSTM预测模型进行参数优选。以IGS中心2015年全年1 h时间尺度的TEC格网数据进行实验分析，结果表明，EEMD-LSTM组合模型的预报结果能够很好的反应电离层TEC的变化特性，在低、中、高纬度地区平均预报残差分别为1.37、0.82和0.96个TECu，预测平均相对精度分别为92.8 %、91.9 %和87.8 %。

长短期记忆神经网络；递归神经网络；总体经验模态分解；电离层总电子含量；时间序列

0 引言

预报电离层总电子含量（total electric contents, TEC）对研究电离层随时间的变化以及以全球卫星导航系统（global navigation satellite system, GNSS）作为主要技术手段的各类工程活动和科学研究都有着重要的意义[1-2]。目前应用国际GNSS服务组织（International GNSS Service, IGS）提供的格网数据建立高精度的TEC预报模型已经从传统的统计学和计量经济学模型[3-4]逐渐发展为学习能力更为优秀以及在处理非线性与时变性问题上更有优势的神经网络模型[5-8]。然而传统的前馈式神经网络预测模型的静态特性无法很好的表示TEC时间序列的动态变化情况，对电离层TEC值的预报精度很难进一步提升。递归神经网络（recurrent neural network, RNN）是一种具有记忆功能的深度学习模型[9]，能够记忆以往时间序列的信息并加入到当前的输出计算中，被广泛应用于序列化数据分析和预测中。长短期记忆（long-short term memory, LSTM）模型[11]改进了RNN在反向传播过程中计算参数更新值时会出现梯度爆炸梯度消失等缺点，可以学习长期依赖时序信息。文献[11]首先利用经验模态分解（empirical mode decomposition, EMD）的方法对电离层TEC时间序列进行分解变换，再对分解后的各个序列分别建立模型进行预报，有效的提高了TEC值预报精度[11]，而采用EMD对TEC时间序列进行分解变换常常会导致模态混叠的现象出现。

针对于以上问题，本文采用总体经验模态分解（ensemble empirical mode decomposition, EEMD）[13]与长短期记忆神经网络模型相结合的方法对电离层TEC值进行短期预报，并通过网格搜索对组合模型的进行超参数优选。最后，利用平均绝对误差（mean absolute difference, MAD）、平均相对精度（relative accuracy, RA）和均方根误差（root mean square error, RMSE）3个性能指标来评估模型的有效性。

1 算法原理

1.1 递归神经网络

递归神经网络是一种可以有效提取、利用和处理时间序列的高维非线性动力学系统。图1为一个标准的RNN模型及其内部结构示意图，可以看出递归神经网络是一个拥有重复单元的循环式模型。

图1 RNN模型及循环层内部结构图

LSTM模型神经元结构如图2所示。

图2 LSTM模型神经元结构示意图

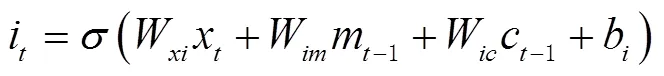
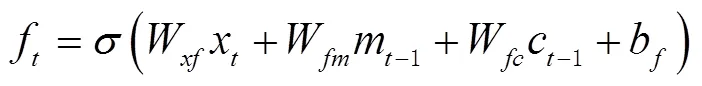
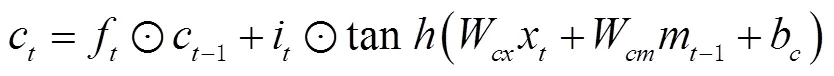
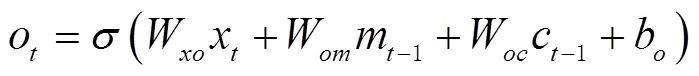
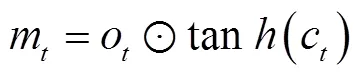
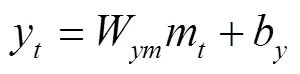
1.2 总体经验模态分解（EEMD）

经验模态分解实质是对原始信号中不同尺度的信号和趋势进行筛分，得到有限个特征单一的不同频率的本征模态分量（intrinsic mode function, IMF）和一个趋势序列。各个IMF分量可以看作是影响原始信号的不同因数，趋势项则反映了原始信号的整体变化趋势。EMD在分解TEC时序信号时由于TEC时序中一些高频信号与噪声频率接近，导致模态混叠现象的出现。总体经验模态分解（EEMD）在原始TEC时序信号中加入高斯白噪声再进行多次EMD分解，并将多次分解得到的IMF总体平均得到最终的IMF分量，有效的避免了模态混叠问题。由于高斯白噪声具有不相关随机序列零均值特性，整体平均后可以将高斯白噪声剔除。高斯白噪声振幅值（所加白噪声占原始信号幅值标准差的比例）和重复进行EMD分解的次数是EEMD分解的两个重要参数，通过不断实验进行调整。

1.3 网格搜索与k折交叉验证

1.4 研究方法

LSTM模型的算法流程图如图3所示，主要包括3个部分：原始TEC时序数据预处理、模型的超参数优化和模型的建立和预测。

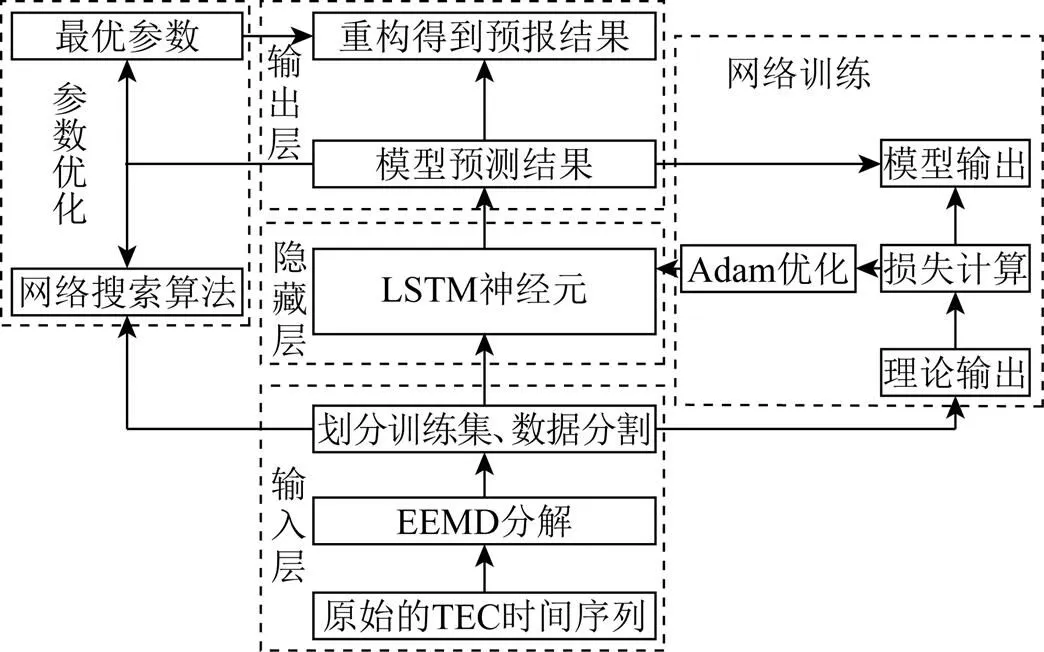
图3 LSTM模型的算法流程图

具体计算过程如下：

1）EEMD分解：选区高斯白噪声0.2倍标准差，加入到TEC时间序列中，对复合序列进行100次EMD分解得到一系列不同频率且特征单一的IMF分量。

2）模型训练：对得到的各分量和趋势项进行标准化建立LSTM模型,激活函数为线性函数，优化器为Adma算法，目标函数为均方差。

4）模型预测：利用训练好的模型采用迭代的方法进行预测。

5）精度评定：将预测结果与IGS提供的观测数据进行比较，采用MAD、RMSE和RA 3个性能指标来评估模型的有效性，当MAD、RMSE值越小RA值越大时，表明预测值与真实值拟合程度更好，俩者的误差越小，其相应的定义为

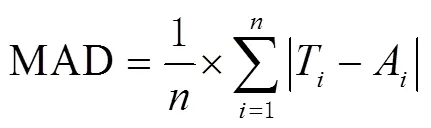
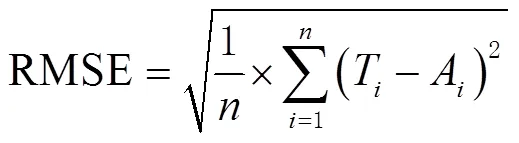
2 实验分析

分别以IGS提供的2015年时间间隔为1 h的全年的高纬度（67.5°N, 65°E）、（67.5°N, 125°E）；中纬度（45°N, 65°E）、（45°N, 125°E）和低纬度（22.5°N, 65°E）、（22.5°N, 125°E）数据建立电离层样本序列。将所选数据分为3个部分，以65 %的数据作为训练集训练模型，以30 %的数据作为验证集来辅助模型的构建，以5 %的数据作为测试数据用于评估模型的精度。

2.1 超参数优选

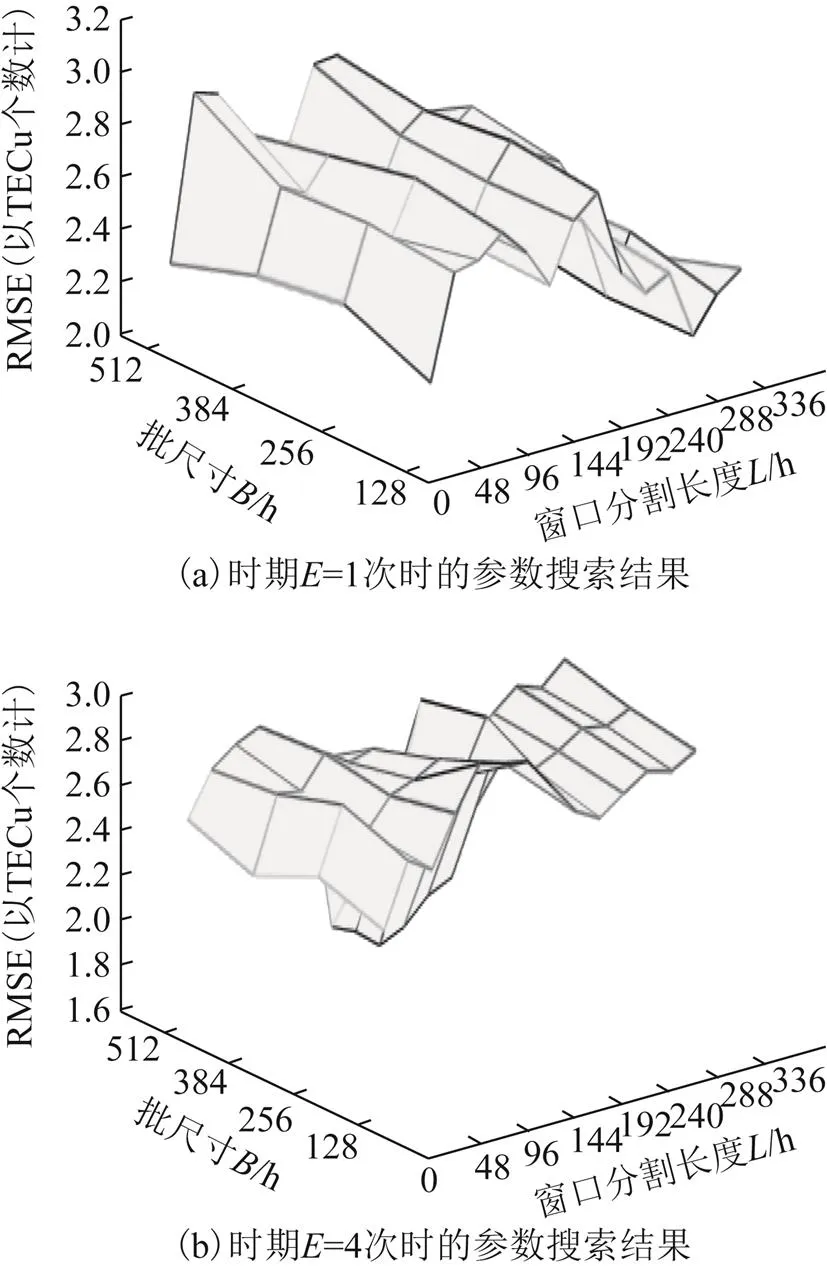
图4 LSTM模型3参数多层网格搜索结果

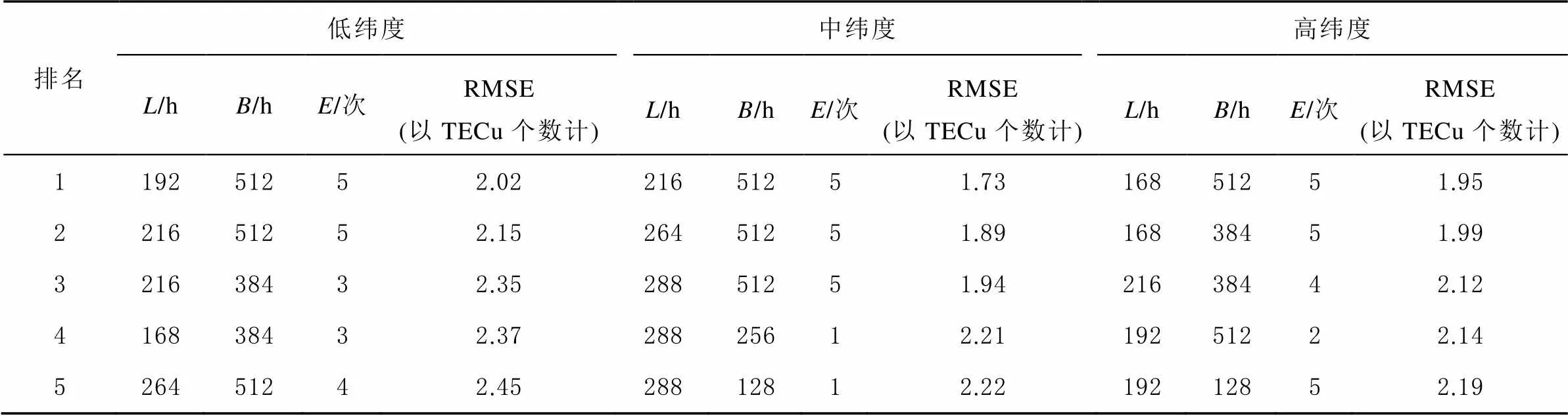
表1 LSTM模型的前五组最优参数组合以及预测精度

2.2 不同模型的精度分析

为了验证LSTM模型的预报精度，采用BPNN模型和RNN模型进行对比分析。以预测拟合电离层TEC值图形与计算误差的形式来实证其差异。图5为RNN、LSTM、BPNN 3种模型的预报结果对比图。其中横坐标为预测历元的个数，1 h为一个历元；纵坐标表示TEC值（以TECu个数计）。由图5可以看出相较于其他模型LSTM模型的预测结果明显优于RNN模型和BPNN模型，能够更好的拟合IGS中心提供的TEC值，误差更小。

计算不同模型在不同纬度预测结果的性能指标得到表2，可以看出LSTM模型的MAD和RMSE的值是上述模型中最小的，即LSTM模型的预测误差比BPNN、RNN模型都小，预测精度更高。同时LSTM模型的预报精度在不同纬度地区的略有差异，低纬度和高纬度地区预报结果的平均绝对百分比误差明显高于高纬度地区，这是由于在不同纬度地区TEC值含量有很大不同所导致的。

表2 不同模型预报结果的MAD、RMSE和RA统计表

为了验证EEMD算法对LSTM模型的预测性能的改进效果，分别采用单一的LSTM模型和EEMD-LSTM组合模型对2015年不同经纬度数据进行24 h预报，以预测拟合电离层TEC值图形与计算误差的形式来实证其差异。图6为EEMD-LSTM模型和单一的LSTM模型在不同经纬度地区的预报结果对比图。其中横坐标为预测历元的个数，1 h为1个历元；纵坐标表示TEC值，单位为TECu的个数。可以看出相较于单一模型EMD-LSTM模型的预报结果能更好的反应电离层TEC值的变化情况，预测性能更好，且预报结果与IGS中心提供的TEC值更为接近，误差更小。

计算单一LSTM模型和EEMD-LSTM组合模型在不同经纬度预测结果的性能指标得到表3和表4，可以看出在同一位置组合模型的预测精度普遍高于单一模型。在经度相同时预测的相对精度大致随着纬度的增加而降低，均方根误差和平均绝对误差则在高纬度地区更优；纬度相同时不同经度之间的预报结果相差不大。

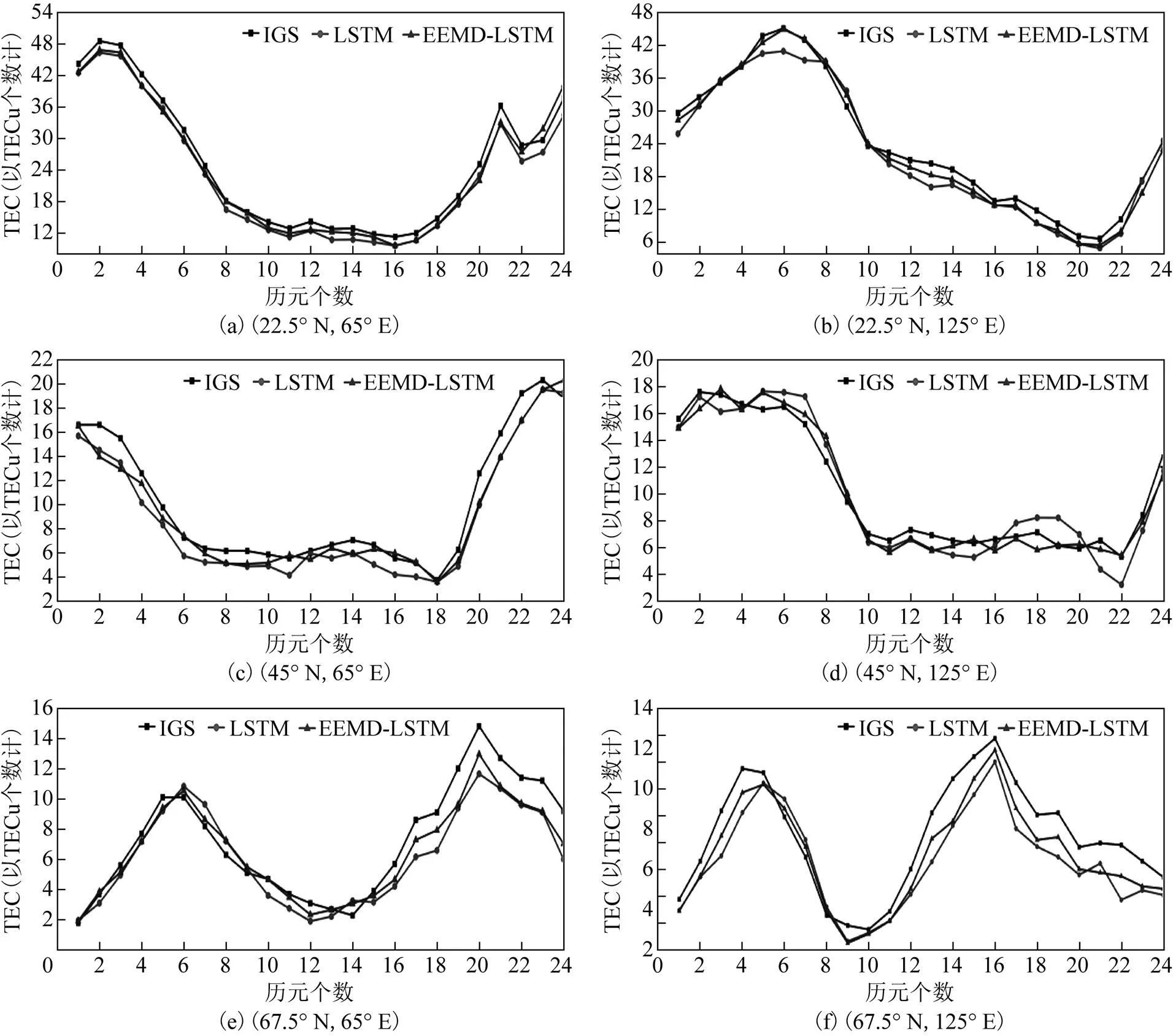
图6 LSTM/EEMD-LSTM模型预报结果对比图

表3 LSTM/EEMD-LSTM模型预报结果的MAD、RMSE和RA统计表（65°E）

表4 LSTM/EEMD-LSTM模型预报结果的MAD、RMSE和RA统计表（125°E）

3 结束语

本文首先对比了单一LSTM模型和EEMD-LSTM模型的在相同环境下的预报性能，验证了组合模型的优越性，并以测试集上预测结果的均方根误差最小为目标，运用多层网格搜索算法对EMD-LSTM预测模型进行参数优选，经过大量实验得到如下结论：

1）与一般BP神经网络相比，递归神经网络的拟合和预测性能更优。LSTM作为递归神经网络的一种变体，可以充分利用长距离的TEC时序信息来实现更好的预测效果。

2）相较于单一LSTM模型EEMD-LSTM模型预报效果和精度都有很好的提升，与实际数据吻合更好；在低、中、高纬度地区预测平均相对精度分别提高了2.8 %、5.8 %和6.6 %。

[1] 张小红, 任晓东, 吴风波, 等. 震前电离层TEC异常探测新方法[J]. 地球物理学报, 2013, 56(2): 441-449.

[2] 曹华东, 郭金运, 李旺, 等. 2015年4月20日花莲M_W6. 4级地震震前电离层TEC异常[J]. 地球物理学进展, 2016, 31(5): 1889-1894.

[3] 张小红, 任晓东, 吴风波, 等. 自回归移动平均模型的电离层总电子含量短期预报[J]. 测绘学报, 2014, 43(2): 118-124.

[4] 谢劭峰, 陈军, 黄良珂, 等. 基于Holt-Winters的电离层总电子含量预报[J]. 大地测量与地球动力学, 2017, 37(1): 72-76.

[5] 何春梅, 模糊神经网络的性能及其学习算法研究[D]. 南京: 南京理工大学, 2010, 19-30.

[6] 袁景凌, 钟珞, 李小燕. 灰色神经网络的研究及发展[J]. 武汉理工大学学报, 2009, 31(3): 91-93.

[7] 李淑慧, 彭军还, 徐伟超, 等. 利用神经网络预报短期电离层TEC变化[J]. 测绘科学, 2013, 38(1): 8-9, 12.

[8] 王建敏, 黄佳鹏, 祝会忠, 等. 电离层总电子数预报方法研究[J]. 测绘科学, 2016, 41(12): 47-52.

[9] 张承钊. 一种金融市场预测的深度学习模型: FEPA模型[D]. 成都: 电子科技大学, 2016.

[10] 王鑫, 吴际, 刘超, 等. 基于LSTM循环神经网络的故障时间序列预测[J]. 北京航空航天大学学报, 2018, 44(4): 772-784.

[11] 汤俊, 姚宜斌, 陈鹏, 等. 利用EMD方法改进电离层TEC预报模型[J]. 武汉大学学报(信息科学版), 2013, 38(4): 408-411, 444.

[12] 袁天娇, 陈艳红, 刘四清, 等. 基于深度学习递归神经网络的电离层总电子含量经验预报模型[J]. 空间科学学报, 2018, 38(1): 48-57.

[13] WU Z H, HUANG N E. Empirical model decomposition: a noise-assisted data method[J]. Advances in Adaptive Data Analysis, 2009, 1 (1): 1-14.

[14] NAKAMURA M I, MARUYAMA T, SHIDAMA Y. Using a neural network to make operational forecasts of ionospheric variations and storms at Kokubunji, Japan[J]. Earth Planets & Space, 2007, 59(12): 1231-1239.

[15] LI S, LI L, PENG J. Variability of ionospheric TEC and the performance of the IRI-2012 model at the BJFS station, China[J]. Acta Geophysical, 2016, 64(5): 1970-1987.

TEC prediction of ionosphere based on deep learning LSTM model

JI Changdong1, WANG Qiang1, WANG Guipeng2, LIU Yanan1

（1.School of Geomatics, Liaoning Technical University, Fuxin, Liaoning 123000, China; 2. Rizhao Geotechnical Investigation and Surveying Institute of Urban and Rural Construction Co., Ltd, Rizhao, Shandong 276800, China）

The total electron content (TEC) is a representative parameter. For its non-linear and non-stationary characteristics taking the TEC data which varies from high latitude to low latitude in both quiet and active period provided by the IGS as sample data. A new combined forecasting model is built in this paper by using ensemble empirical mode decomposition (EEMD) and Long-Short Term Memory Model (LSTM). Furthermore, a multilayer grid search algorithm is proposed to optimize the parameters of EMD-LSTM prediction model. Results from numerical experiments show that the predicted results are highly fitted to the actual observation data. The average prediction residuals in different latitudes are 1.37TECu, 0.82TECu and 0.96TECu, respectively. The predicted average relative accuracy is 92.8 %, 91.9 % and 87.8 %, respectively.

LSTM; RNN; EEMD; TEC; Time series

TN967.1

A

2095-4999(2019)03-0076-06

2018-10-22

吉长东（1970—），男，辽宁锦州人，博士，教授，研究方向为卫星导航与定位。

王强（1993—），男，内蒙古乌兰察布人，硕士生，研究方向为卫星导航与定位。

吉长东，王强，王贵朋，等.深度学习LSTM模型的电离层总电子含量预报[J].导航定位学报,2019,7(3):76-81.（JI Changdong, WANG Qiang, WANG Guipeng, et al.TEC prediction of ionosphere based on deep learning LSTM model[J].Journal of Navigation and Positioning,2019,7(3):76-81.）

10.16547/j.cnki.10-1096.20190313.