基于混沌扰动机制的天牛须搜索算法及其在图像增强中的应用
马吉明 陈浩洋 张嵩


关键词:
天牛须搜索算法;混沌扰动;图像增强;灰度值
摘要:针对天牛须搜索算法(BAS)收敛速度慢、精度低、全局搜索效果较差等问题,提出了一种基于混沌扰动机制的改进天牛须搜索算法(CDBAS).该算法通过混沌机制对天牛位置进行扰动,在迭代时先进行全局搜索,找到全局适应度值大的区域,然后在该区域中再进行搜索.对BAS和CDBAS分别用7个测试函数进行实验对比,结果显示CDBAS算法具有更好的优化性能,其收敛速度更快,求解精度更高.将CDBAS算法应用于图像增强中,结果表明,CDBAS算法的增强效果更为明显,图像更加清晰,层次信息更为丰富.
Abstract:To solve the problem of slow convergence,low precision and poor global search effect of beetle antennae search algorithm (BAS), an improved beetle antennae search algorithm (CDBAS) based on chaotic disturbance mechanism was proposed.The algorithm disturbed the position of longicorn by chaotic mechanism, searched the region with large global fitness value first in iteration, and then searched in the region.Comparation of BAS and CDBAS with 7 test functions showed that CDBAS algorithm had better optimization performance, faster convergence speed and higher accuracy.The CDBAS algorithm was applied to image enhancement. The results showed that the enhancement effect of CDBAS algorithm was more obvious, the image was clearer and the hierarchical information was more abundant.
0 引言
启发式算法在以计算机科学为主要内容的学术社会,以及许多其他实际工程领域中发挥着相当重要的作用,比如背包问题求解[1]、神经网络[2]、PID控制策略[3]、K均值分类[4]、多聚焦图像融合[5]的实现等.启发式算法是相对最优化算法提出的,最优化算法可以求出一个问题中每个实例的最优解,而启发式算法是一个基于直观或经验构造的算法,在可接受的花费(指计算时间和空间)下给出待解决组合优化问题每一个实例的一个可行解,该可行解与最优解的偏离程度一般不能被预计.由于启发式算法具有简单、灵活和局部最优等特点,在过去几十年中引起了业内学者的广泛关注.S.Mirijalili等[6]提出了一个灰狼优化器,通过在自然界中模仿灰狼的领导和猎物,使其较强的收敛性能为快速求解出最优值做好铺垫.X.S.Yang等[7]受到一些杜鹃种群繁殖寄生的启发,开发了一种名为杜鹃搜索的算法用于优化搜索.乔东平等[8]研究一种蚁群优化方法,该方法受某些蚂蚁种群觅食行为与方法的启发,以探索优化问题的方案.T.Q.Wu等[9]模仿海豚在搜寻、呼叫、接受、捕猎中,进行回声定位、信息交流、合作分工等行为,提出海豚算法.本文研究的内容为图像增强,需要对图像进行优化.为了解决优化问题,本文选择了X.Y.Jiang等[10]在2018年提出的启发式算法,即天牛须搜索算法(BAS),该算法模拟了天线的功能和自然界中甲虫的随机行走机制,实现了检测和搜索两个主要步骤,具有求解速度快、精度高等特点.BAS算法不需要梯度信息和函数的具体形式,就可以实现高效寻优与求解.相对于粒子群算法,BAS算法只需要一个个体,即一只天牛,因此算法运算量较低.
本文拟综合混沌扰动优化策略的思想,在基本的BAS算法基础上,提出一种基于混沌扰动机制的天牛须搜索算法(CDBAS),采用混沌扰动机制优化天牛位置,解决BAS易限于局部极值、收敛速度慢的问题,并将其应用到图像处理领域,以期获得更好的图像增强效果.
1 基于混沌扰动机制的天牛须搜索算法1.1 BAS算法的基本原理
BAS算法是一种受天牛觅食原理启发的智能优化算法.天牛觅食是根据食物气味的强弱来觅食的.天牛的触角非常长,有的甚至超过了身体的长度,大触角扩大了探索的区域.如果左边触角收到的氣味比右边大,天牛就往左边飞,否则就往右飞,直至找到食物.
其中,xr是右侧搜索区域的位置;xl是左侧搜索区域的位置;d是与利用能力相对应的天线的传感长度,该长度需要足够长,能覆盖适当的搜索范围,以便从开始就能从局部最小点跳出,然后随着时间t的推移,传感长度逐渐缩短.
在BAS算法中,由于天牛须是单个个体搜索,不是群搜索,所以它的全局搜索效果较差,不能在大范围内找出理想的结果.因此需要进行改进,使其能够在大范围内搜索出最佳的适应度值.
1.2 混沌扰动机制
混沌是一种确定的但又不可预测的运动状态,在有限空间中永远运动着,不相交也不闭合,它是自然界普遍存在的一种非线性现象,它看似混乱,却有着精致的内在结构,具有随机性、遍历性、规律性等特点[11].
1.3 改进的天牛须搜索算法
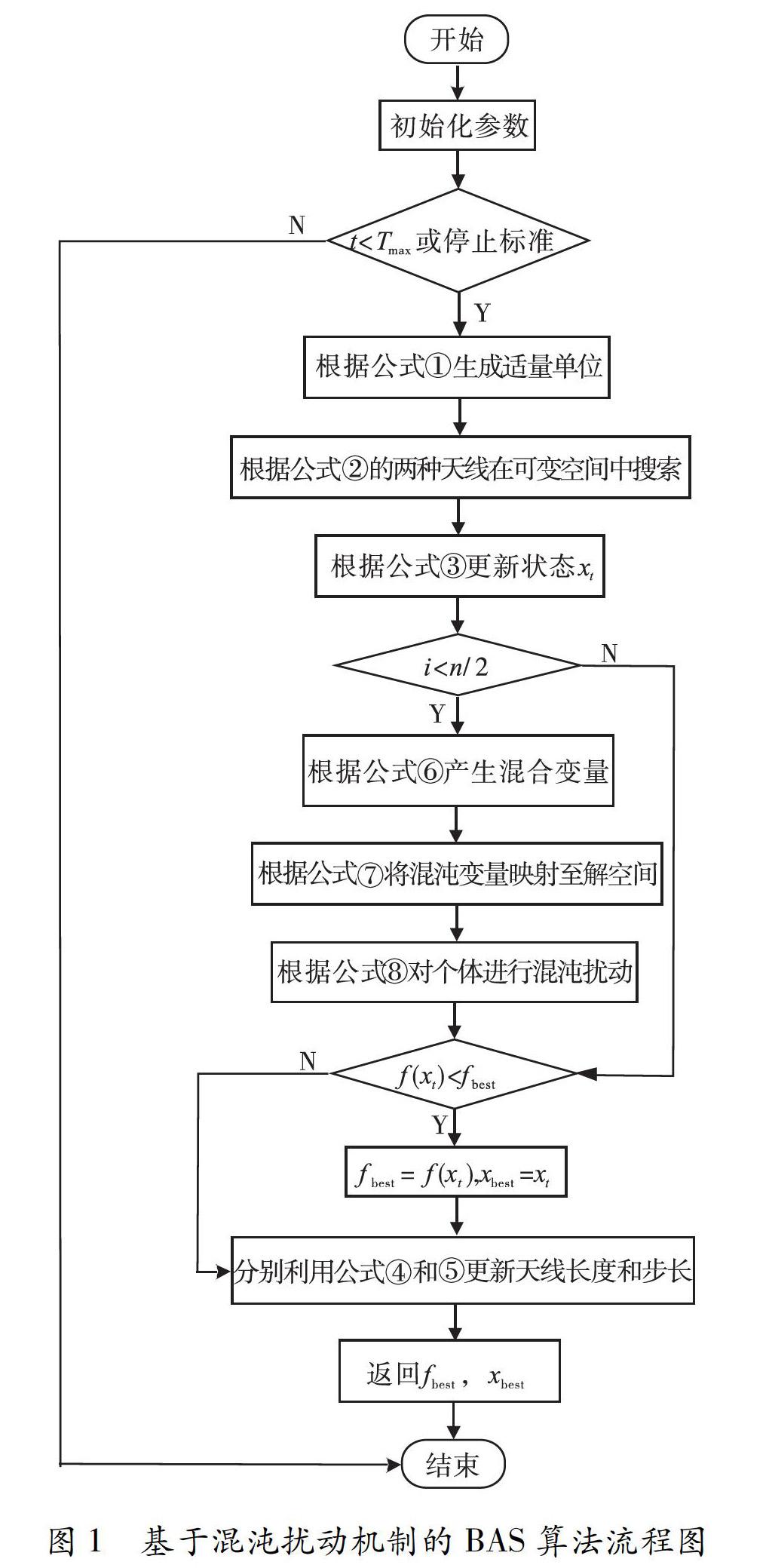
混沌搜索是一种效果较好的搜索机制,由于它具有遍历性,利用混沌变量进行优化搜索会比盲目无序的随机搜索更具优越性,所以将混沌扰动机制引入BAS,可以在搜索时更容易跳出局部极值[13].CDBAS算法开始进行迭代时,前一部分迭代采用混沌扰动机制进行全局搜索,后一部分迭代根据原始行为进行局部搜索,这可以加快算法的收敛速度,提高算法的收敛精度.CDBAS算法的流程如图1所示.
初始化参数之后,如果没有超过迭代次数,则先生成一个天牛的随机方向,再通过气味等相关信息更新方向,迭代的前一部分根据混沌扰动机制进行搜索,后一部分根据原始的行为搜索.不管是前一部分迭代还是后一部分迭代,只要发现有更好的适应度值,就进行替换,直到迭代结束.
在前一部分的迭代过程中,扰动分量较大,因此进行全局搜索,在全局中找到适应度值大的区域.在后半部分的迭代中,对前一部分选中的区域进行再搜索,这时扰动分量较小,收敛精度较高.扰动次数随着迭代次数的增加而减少,
这种“全面撒网,重点捞鱼”的行为,弥补了BAS算法的不足,能对收敛速度、求解精度更好地进行优化.
2 仿真实验与分析
2.1 仿真实验设计
2.2 实验结果及分析
2.2.1 精度对比 将所得最优值、最差值、平均值和方差作为算法精度和鲁棒性的衡量指标,运行结果如表2—表4所示.
从表2—表4可以看出,当测试函数在2维、10维和20维时,CDBAS算法总体上比BAS算法的精度更高、鲁棒性更好.CDBAS继承了BAS的优点,又增强了全局搜索能力,极易于跳出局部极值,同时扰动量随着迭代次数的增加不断减小,利于局部搜索.
2.2.2 进化曲线对比 由于2维、10维、20维不同函数的运行结果具有相同的变化趋势,所以本文选取20维的进化曲线进行对比,进化曲线如图2所示.
从图2可以看出,在相同维数和参数条件下,对于所有的函数,CDBAS的收敛速度远远优于BAS.这是因为BAS算法收敛到极值后,找不到一种有效机制能使算法跳出局部极值.
3 CDBAS算法在图像增强中的应用
由图3和图4可知,输入图像的灰度值很低,使用CDBAS算法后,增强了图像的灰度值,并且图像的清晰度更高,亮度更亮,视觉效果得到了很好的改善,鲁棒性增强;与BAS算法相比,CDBAS增强的直方图的灰度值范围更大,层次也更加丰富.
4 结语
本文提出的CDBAS算法,在BAS算法的基础上,引入了混沌扰动机制对天牛位置进行扰动,扰动量随着迭代次数的增加不断减小.运用7个标准测试函数分别在2维、10维、20维进行对比实验,验证了CDBAS算法相比于BAS算法的收敛速度和求解精准度更优.将CDBAS算法应用于图像增强,增强效果比BAS算法更加明显,图像更加清晰,層次信息更为丰富.为了扩展改进的天牛须算法的应用领域,下一步将研究该算法在多目标规划问题中的应用.
参考文献:
[1] 李佩泽,王姗姗,樊岩.基于改进蝙蝠算法的背包问题求解[J].计算机应用研究,2015(11):3226.
[2] 冷昕,张树群,雷兆宜.改进的人工蜂群算法在神经网络中的应用[J].计算机工程与应用,2016,52(11):7.
[3] 程准,鲁植雄,唐迪,等.基于改进PSO算法的拖拉机驱动防滑PID控制策略[J].计算机应用研究,2017,34(1):83.
[4] 王晓东,张姣,薛红.基于蝙蝠算法的K均值聚类算法[J].吉林大学学报(信息科学版),2016,34(6):805.
[5] 费春,张萍,李建平.基于人工鱼群优化分块的多聚焦图像融合[J].强激光与粒子束,2015,27(1):1
[6] MIRJALILI S,MIRJALILI S M,LEWIS A.Grey wolf optimizer[J].Advances in Engineering Software,2014,69(3):46.
[7] YANG X S,DEB S.Cuckoo search:recent advances and applications[J].Neural Computing and Applications,2014,24(1):169.
[8] 乔东平,裴杰,肖艳秋,等.蚁群算法及其应用综述[J].软件导刊,2017(12):217.
[9] WU T Q,YAO M,YANG J H.Dolphin swarm algorithm[J].Frontiers of Information Technology & Electronic Engineering,2016,17(8):717.
[10] JIANG X Y,LI S.BAS:Beetle antennae search algorithm for optimization problems[J].International Journal of Robotics and Control,2018,1(1):1.
[11] 李兵,蒋慰孙.混沌优化方法及其应用[J].控制理论与应用,1997(4):613.
[12] 江铭炎,袁东风.人工蜂群算法及其应用[M].北京:科学出版社,2014.
[13] ALATAS B.Chaotic bee colony algorithms for global numerical optimization[J].Expert Systems with Applications,2010,37(8):5682.
[14] TUBBS J D.A note on parametric image enhancement[J].Pattern Recognition,1987, 20(6):617.
[15] GONZALE R C,WOODS R E.数字图像处理(MATLAB版)[M].2版.阮秋琦,译.北京:电子工业出版社,2003.

