基于FFT和复域相关的光纤EFPI压力传感器多腔长解调方法*

何文涛 赵光再 宁佳晨 李金洋 史 青

基于FFT和复域相关的光纤EFPI压力传感器多腔长解调方法*

何文涛 赵光再 宁佳晨 李金洋 史 青

（北京遥测技术研究所 北京 100076）

为实现高温光纤压力传感器的温度补偿，将基于高斯拟合FFT算法与复域相关算法结合，提出一种多腔解调方法。算法首先采用基于高斯拟合的FFT算法，粗解算出各腔的大致腔长，再利用复域相关算法在小范围内解调出各个腔长的精确值。方法降低对FFT解调精度要求，并缩小相关解调算法中的虚拟腔长范围，提高解调精度和效率。最后以初始腔长为50μm、110μm和250μm进行仿真验证，算法解调精度优于10nm，证明了多腔长解调算法的有效性和准确性。

多腔长解调算法；光纤EFPI压力传感器；高斯拟合；互相关

引 言

基于非本征法布里-珀罗干涉EFPI（Extrinsic Fabry-Perot Interferometry）的光纤感器是近年来高温传感领域的研究热点，利用相干光的干涉原理检测法-珀（F-P）腔微位移来实现待测物理量的测量，具有体积小、分辨率高、灵敏度高等特点，广泛应用于压力、变形和温度等参量的测量[1-4]。通过多个腔的组合，该种传感器还能实现多个物理量的复合测量[5,6]。

EFPI传感器腔长解调方法根据解调原理大致可分为两大类：第一类为光强解调，主要是寻求线性最佳点，在线性工作点实现EFPI腔的高速解调[7,8]；另一类是相位解调，这类解调方法以宽光谱下测量出的光强为基础，通过谱型分析实现腔长解调，主要应用于准静态、高精度腔长解调场合[9,10]。基于光强解调原理的解调方法易受到光纤所处环境温度、弯曲半径以及气压等综合因素的影响，解调具有不确定性；为改善此类方法，Schmidt等提出三波长解调，引入参照光削弱光强对解调的影响，实现了解调速度和精度的同时提升，但是不适用于多腔长的同时解调[11]。在采用相位方式解调腔长的算法中，多数学者采用快速傅里叶（FFT）算法解算[12-15]，文献[12]对采集的光谱直接进行了波长域的FFT变换，无插值运算，解调精度较低；文献[13]采用能量重心法与FFT变换项结合的方法，进一步提升了FFT解调精度，但是提升精度受限于光谱模块的分辨率；文献[14]采用相关的解调算法，在整个腔长范围内搜索解调，具有较高的精度，但解调算法效率低。文献[15]采用单一余弦相关函数求取腔长，在腔长附近存在振荡，需要再进行拟合包络解算最大值，降低了解算速率和精度。

本文采用复域相关法求取腔长，避免在相关极大值附近出现振荡现象。为降低解调算法运算量，本文首先采用基于高斯拟合的FFT算法粗略预估各个腔长，缩小腔长扫描范围；再采用复域相关算法实现对不同腔长的高精度解调。

1 基于高斯拟合FFT和复域相关的多腔长解调方法

1.1 EFPI高温压力传感器

EFPI高温压力传感器的典型结构如图1所示，通常由压力敏感芯片、金属外壳、基座、准直结构以及耐高温光纤等部分构成。从光纤发射出的光经过敏感芯片后从不同反射面返回后发生干涉，构成三个主要的F-P腔。其中F-P腔1、3为固体腔，对温度敏感；F-P腔2为空气腔，对压力、温度均敏感。传感器工作于高温环境时，不能直接通过腔2的长度解算出压力值，需要求解1、3的腔长反演工况温度并结合温度补偿算法实现高温压力的测量。

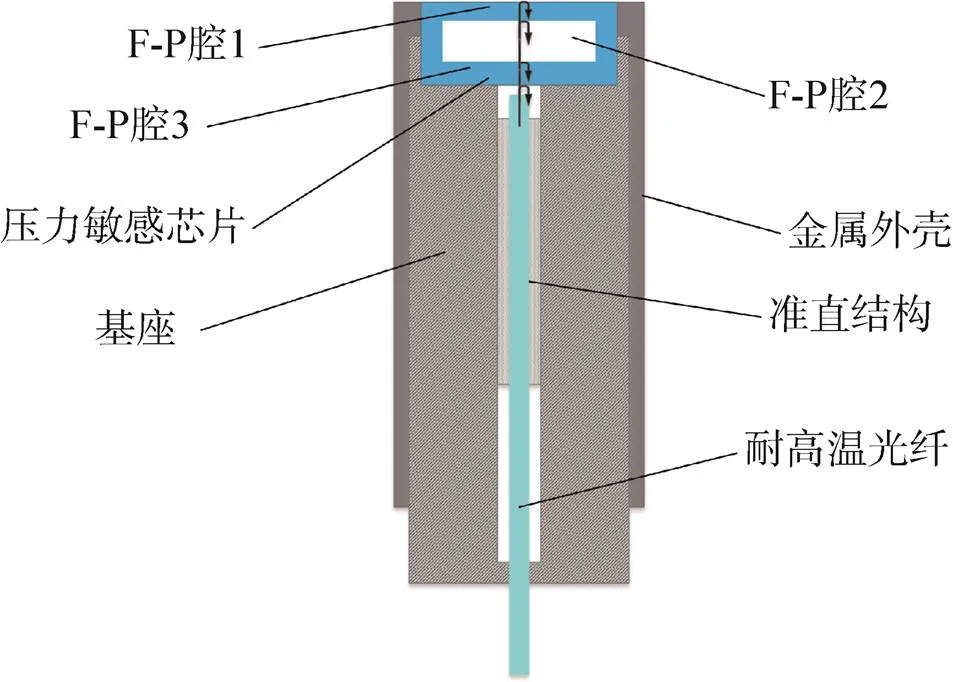
图1 高温EFPI压力传感器结构

1.2 基于高斯拟合FFT的多腔长粗解调

EFPI传感器腔的工作原理是基于多光束干涉，对于单个腔长，其反射光的光强和腔长的关系

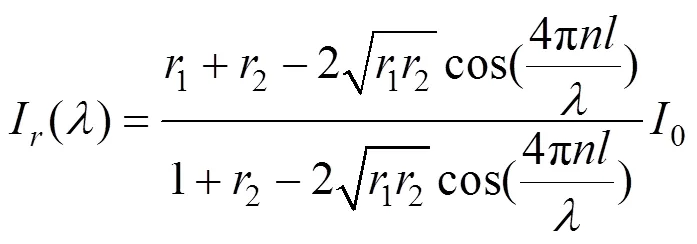
其中，1、2分别是腔体端面的反射率，0是入射光强（假设入射光强频谱是平坦的），是干涉腔长。当两端面的反射率较低时，并且两端面的反射率一样，存在1=2，式（1）可以近似为

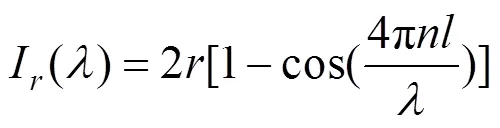
对上式进行傅里叶变换，变换过程如下：

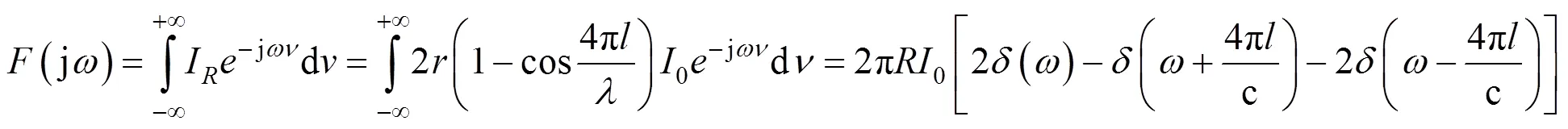
从式（3）可以得出腔长与频率的关系为

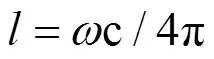
因此，通过傅里叶变换找到幅值极大点，根据对应频率点求取腔长值。

对于包含个腔长的EFPI传感器，各个腔长干涉后的光强满足叠加原理，其反射光强与腔长的关系为

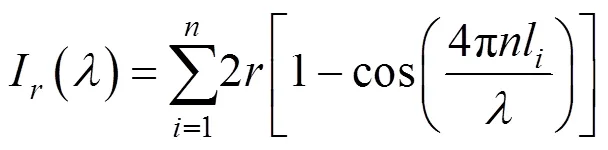
当光源为高斯分布时其傅里叶变换也符合高斯分布，为提升腔长的FFT求解精度，缩小精细解调过程中腔长的寻索范围，采用频域范围内的高斯插值提升解算精度，如图2所示是频域范围内的频谱图。

其中，–11是高斯相邻的数字下标，p是高斯峰值对应的下标，谱型高斯分布，表达式如下：

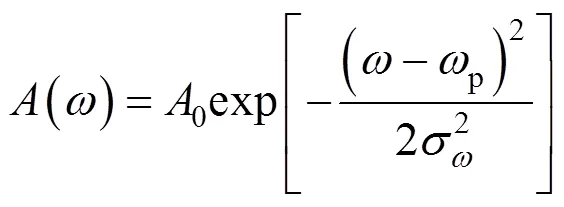
式中p为数字下标p处的数字频率，对上式取对数，其中=2π/，为FFT变换的点数。可以得到

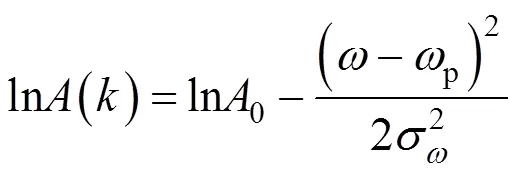
将11分别代入上式，联立方程解得

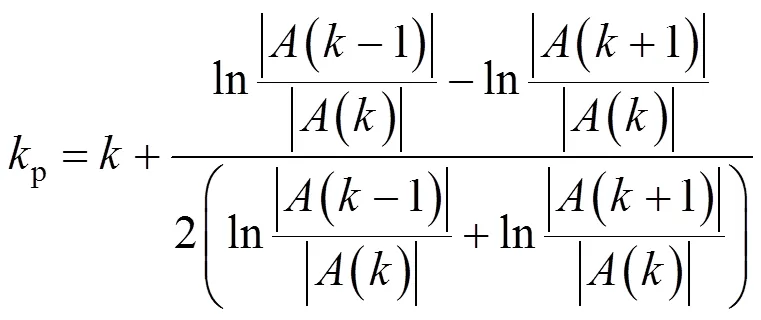
对各个腔长的高斯谱型进行校正，校正后的值代入式（4）求取出腔长1，2，…，l。

1.3 基于复域相关的腔长精解调

根据1.2节、1.3节解调出的腔长l=0，1，……，l，与真实值还存在一定的偏差。对于实际腔长为l，与解调出的腔长l的偏差值记为=l–l，取相关解调的腔长变化范围为（l–δ, l+），且满足

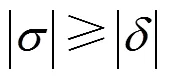
那么，在腔长l附近构建的相关函数为

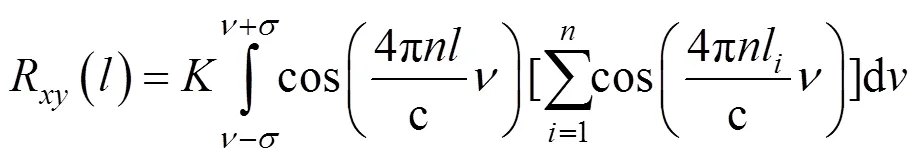
其中=42，通过余弦构建的相关函数，在极大值附近易出现振荡，不利于腔长的高精度求解。为避免在解调腔长附近出现振荡，构建复域的相关函数

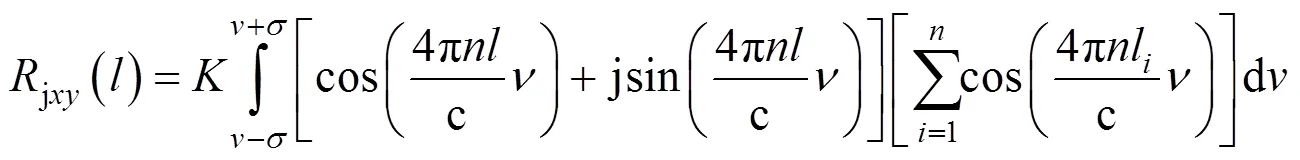
由于实际光谱是离散的，式（10）离散化后得到

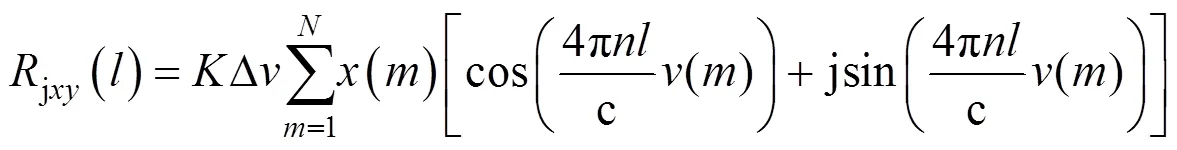
其中，（）为采集到的光谱强度值，是光谱仪CCD阵列像素序号，为光谱模块的采样点数，为避免复域的计算，求取jxy（）的幅值为

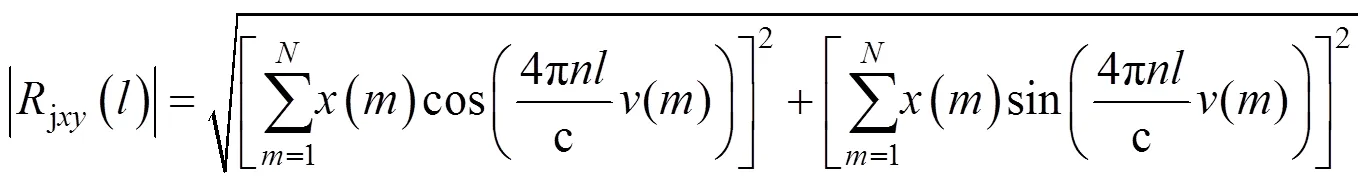
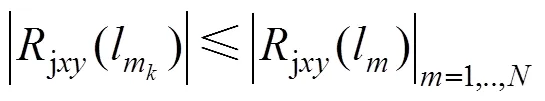
并且此时腔长最接近最真实腔长l，使得

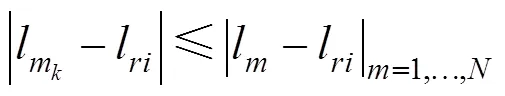
2 算法仿真分析

本文基于FFT与复域相关的多腔长解调算法实现流程如图3所示。

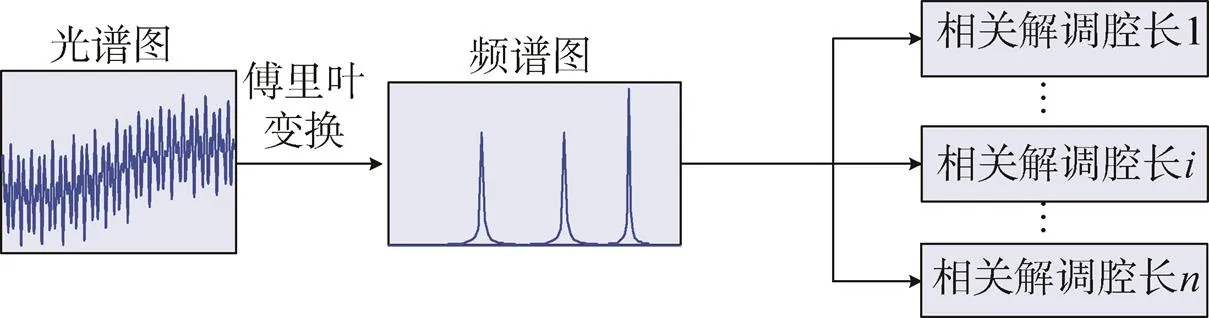
图3 多腔长解调算法的解调流程

仿真以实际参数为基础，采用的光谱解调模块所扫描的波长范围为1510nm~1590nm，测量点数为512个点；光纤EFPI高温压力传感器的腔长分别为110μm、50μm、250μm。采用Matlab软件进行仿真，首先设置腔长2=50μm，3=250μm为恒定值，腔长1在111μm~120μm范围内每隔1μm变化，解调出的腔长值及与真实腔长的误差值如图4（a）所示，解调最大误差控制在7nm以下；同样的，腔长1=110μm、2=50μm为恒定值，腔长3在251μm~260μm范围内每隔1μm变化，解调出的腔长值及与真实腔长的误差值如图4（b）所示，解调最大误差控制在3nm以下；最后，腔长1=110μm，3=250μm为恒定值，腔长2在51μm~60μm范围内每隔1μm变化，解调出的腔长值及与真实腔长的误差值如图4（c）所示，解调最大误差控制在10nm以下。

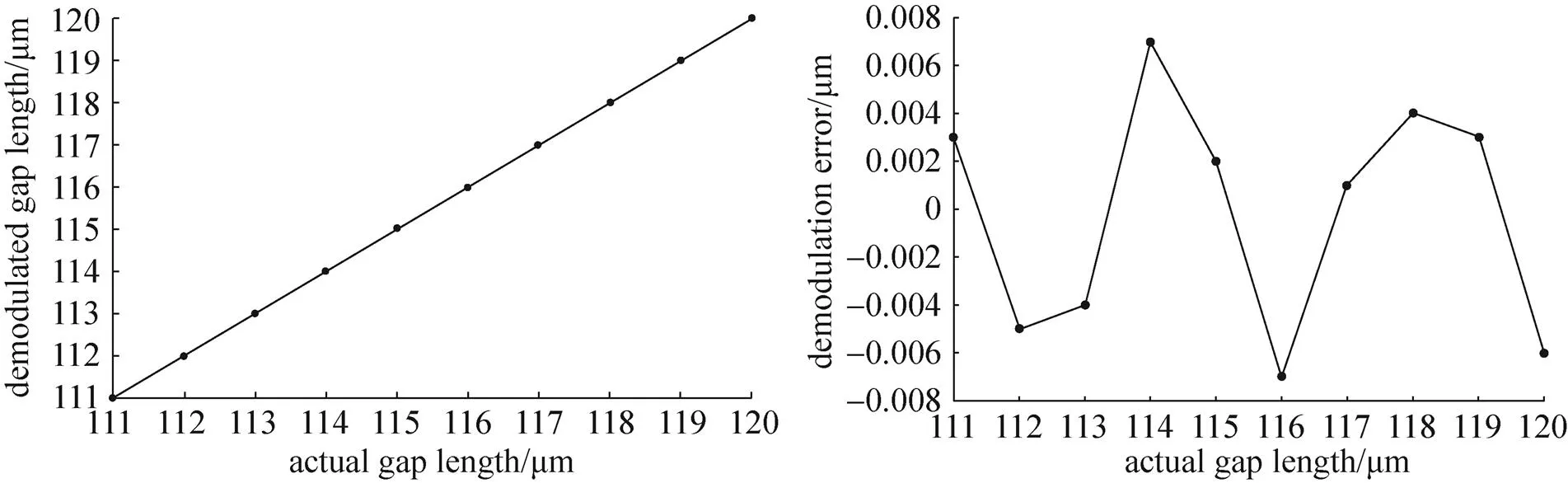
（a）腔长1从111μm变化到120μm

（a）Length of gap 1 changed from 111μm to 120μm

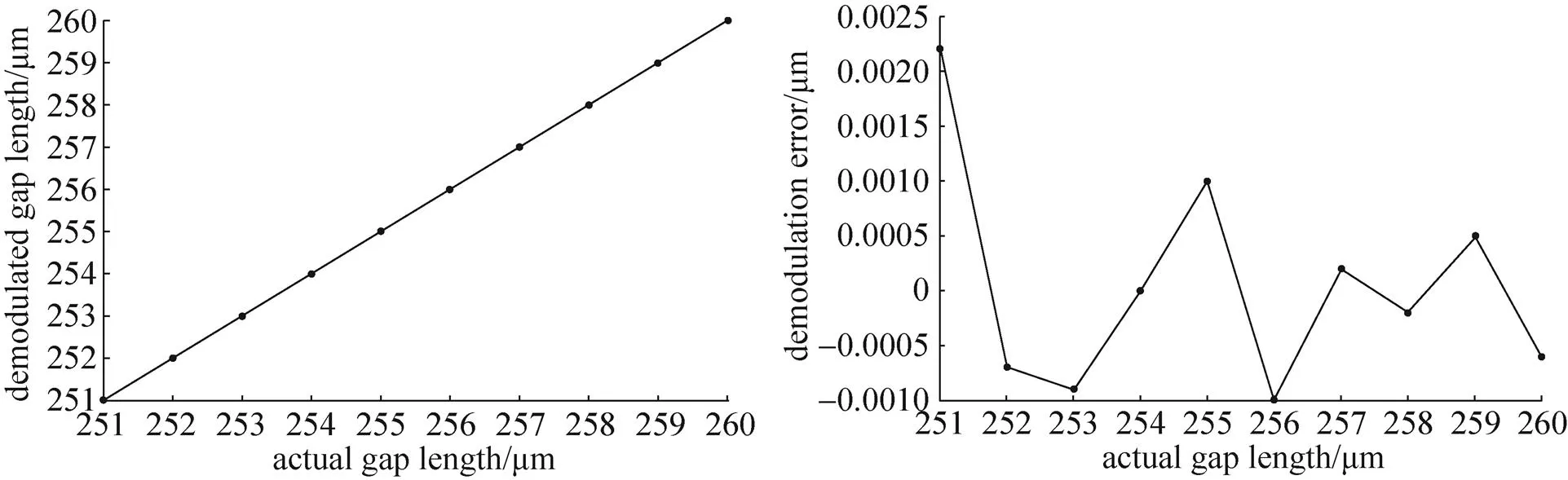
（b）腔长3从251μm变化到260μm

（b）Length of gap 3 changed from 251μm to 260μm

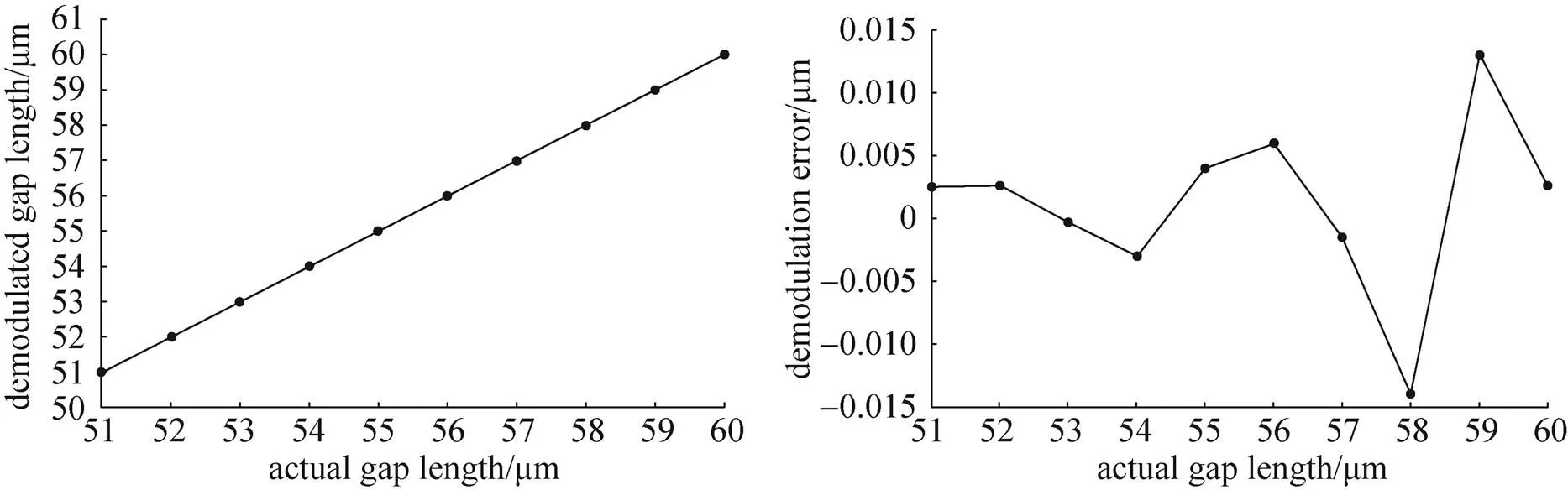
（c）腔长2从51μm变化到60μm

3 算法的计算量分析

采用直接相关法计算腔长时需计算的虚拟腔长范围应大于500μm，若要求分辨率优于1nm，则需进行至少2.56×108次乘法计算；而采用FFT算法直接粗略计算腔长，频率分辨率约为1/D（D为反射光谱的波长范围），以1510nm~1590nm为例，腔长分辨率约为12.5μm，则互相关需进行1.92×108次乘法计算。利用基于高斯拟合的FFT算法可将解调分辨率可提高至优于100nm，使得互相关乘法计算次数降低到3.07×105次，计算效率较前两种算法有明显提升。

4 结束语

针对EFPI压力传感器的多腔长解调，本文提出了采用基于高斯拟合的FFT与相关算法相结合的解调方法。首先，通过FFT解调算法对腔长进行粗解调，确定微米量级误差的各个腔长长度；再根据粗解调出的腔长值构建虚拟腔，进行相关法解调，解调出各个腔长的精确腔长。仿真结果表明解调最大偏差在10nm以下，并大幅减小了计算量，验证了本方法的有效性和准确性。

[1] 李春成, 王鸣, 夏巍等. 基于EFPI腔强度解调的微位移传感器[J]. 光学学报, 2014, 34(6): 0628001_1-0628001_6.

[2] 陈伟民, 王宁, 朱永, 等. 实际光源光谱分布对相位型光纤法珀应变传感器的影响及其实验研究[J]. 中国激光, 2003, 30(1): 88–92.

[3] 张磊. 光纤EFPI-FPG复用温度与压力传感器系统研究[D]. 大连: 大连理工大学, 2009.

[4] 张佩. 基于光纤EFPI传感器的动态解调算法的研究[D]. 武汉: 武汉理工大学, 2009.

[5] OXSENSIS LTD. OPTICAL PRESSURE SENSOR[P]. 美国: US 2015/0020599 A1, 2015.

[6] OXSENSIS LTD. OPTICAL SENSOR[P]. 美国: US 2015/0033848 A1 A1, 2015.

[7] BHATIA V, MUR PHY A, CLAUS R O, et al. Recent develop-ments in optical-fiber-based extrinsic Fabry-Perot interferomet-ric strain sensing technology[J]. Smart Materials and Structures, 1995, 24(4): 246–251.

[8] YU Q X, ZHOU X L. Pressure sensor based on the fiber-opticextrinsic Fabry-Perot interferometer[J]. Photonic Sensors, 2011, 1(1): 72–83.

[9] MA C, DONG B, GONG J, et al. Decoding the spectra of low-finesse extrinsic optical fiber Fabry-Perot interferometers[J]. Optics Express, 2011, 19(24): 23723–23742.

[10] MACPHERSON W N, KIDD S R, BARTON J S, et al. Phasedemodulation in optical fiber Fabry-Perot sensors with inexact phase steps[J]. IEEE Proc-Optoelectron, 1997, 144(3): 130–133.

[11] SCHMIDT M, FURSTENAU N. Fiber-optic extrinsic Fabry-Perot interferometer sensors with three-wavelength digital phase de-modulation[J]. Optics Letters, 1999, 24(9): 599–601.

[12] 章鹏, 朱永, 唐晓初, 等. 基于傅里叶变换的光纤法布里－珀罗传感器解调研[J]. 光学学报, 2005, 25(2): 186–189.

[13] 宋镜明, 吴蓉, 赵文涛. 基于快速傅里叶变换和能量重心联合算法的法布里－珀罗腔长解调方法[J]. 光学与光电技术, 2017, 15(2): 40–45.

[14] 黄海. 光纤法皮传感器腔长解调新方法与系统研究[D]. 重庆: 重庆大学, 2010.

[15] 荆振国. 白光非本征法布里－珀罗干涉光纤传感器及其应用研究[D]. 大连: 大连理工大学, 2010.

Multi-cavities demodulation algorithm of EFPI pressure based on FFT and complex domain correlation

HE Wentao, ZHAO Guangzai, NING Jiachen, LI Jinyang, SHI Qing

（Beijing Research Institute of Telemetry, Beijing 100076, China）

A novel multi-cavities demodulation algorithm, combining the FFT and complex domain correlation, was proposed to realize the temperature compensation of EFPI based pressure sensor using in high temperature environment. Gaussian fitting based FFT was applied to demodulate cavity lengths roughly, and then complex domain correlation was used to calculate the precise lengths in more narrow ranges. This algorithm improved the demodulating precision and efficiency due to decreasing the required precision of FFT and reducing the scope of virtual cross-correlation lengths. Finally, this algorithm was verified by computer simulation with cavities of 50μm, 110μm, 250μm and the result indicate the demodulation was precise within 10nm, which demonstrated the improved algorithm was effective and accurate.

Multi-cavities demodulation algorithm; EFPI pressure sensor; Gaussian fitting; Cross-correlation

TP212.1

A

CN11-1780(2019)03-0017-05

何文涛 1984年生，高级工程师，主要研究方向为高频压力传感技术、超高温传感技术。

赵光再 1987年生，工程师，主要研究方向为光纤传感器信号解调算法。

宁佳晨 1990年生，工程师，主要研究方向为光纤传解调系统软件实现。

李金洋 1988年生，高级工程师，主要研究方向为高温传感器技术。

史 青 1982年生，研究员，主要研究方向为先进光电技术。

战略支援部队装备预先研究项目（30506020302）

2018-08-29

2019-05-14

Email:ycyk704@163.com

TEL:010-68382327 010-68382557